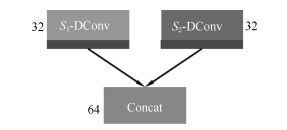
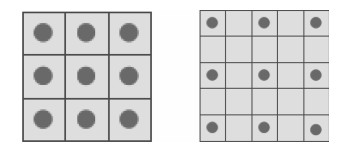
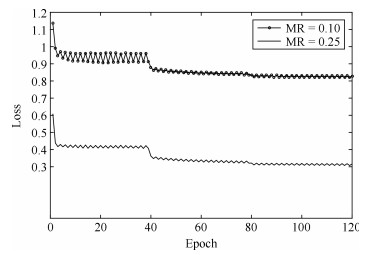
A Compressed Sensing Algorithm Based on Multi-scale Residual Reconstruction Network
-
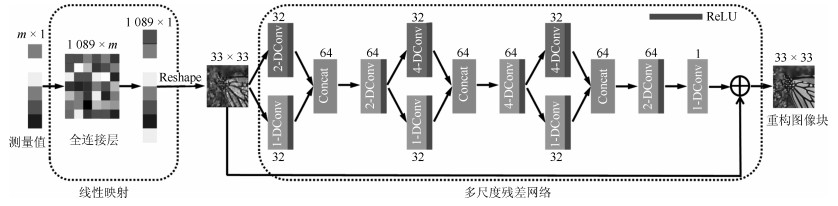
摘要: 目前压缩感知系统利用少量测量值使用迭代优化算法重构图像.在重构过程中，迭代重构算法需要进行复杂的迭代运算和较长的重构时间.本文提出了多尺度残差网络结构，利用测量值通过网络重构出图像.网络中引入多尺度扩张卷积层用来提取图像中不同尺度的特征，利用这些特征信息重构高质量图像.最后，将网络的输出与测量值进行优化，使得重构图像在测量矩阵上的投影与测量值更加接近.实验结果表明，本文算法在重构质量和重构时间上均有明显优势.Abstract: In recent years, a small number of measurements and iterative optimization algorithms were exploited in compressed sensing to reconstruct images. In the process of reconstruction, most algorithms based on iteration for compressed sensing image reconstruction suffer from the complicatedly iterative computation and time-consuming. In this paper, we propose a novel multi-scale residual reconstruction network (MSRNet), and exploit the measurements to reconstruct images through the network. The multi-scale dilate convolution layer is introduced in the network to extract the feature of different scales in the image, and the feature information could improve the quality of reconstructed image. Finally, we exploit the output of the network and measurements to optimize our algorithm, so as to make the projection of the reconstructed image closer to the measurements. The experimental results show that the MSRNet requires less running time and has better performance in reconstruction quality than other compressed sensing algorithms.
-
Key words:
- Compressive sensing /
- convolution neural network /
- multi-scale convolution /
- dilate convolution
1) 本文责任编委 胡清华 -
图 1 多尺度残差重构网络(MSRNet), s-Dconv表示扩张卷积, $s$ = 1, 2, 4
Fig. 1 Mult-scale residuce recontruction network, s-Dconv denotes s-dilate convolution, here $s$ = 1, 2 and 4
图 4 重构图像块修正前后误差的比较(Barbara图像)
Fig. 4 The comparison of the error of the reconstructed image block before and after refined (Barbara)
图 7 比较几种算法的重构性能(第1行到第3行采样率MR = 0.25, 0.10, 0.04)
Fig. 7 Comparison of reconstruction performance of various algotithms (MR = 0.25, 0.10, 0.04)
图 8 修正前后的重构图像对比(MR = 0.25)
Fig. 8 The comparison of reconstructed images before and after refined (MR = 0.25)
表 1 6幅测试图像在不同算法不同采样率下的PSNR
Table 1 PSNR values in dB for six testing images by different algorithms at different measurement rates
图像 算法 MR = 0.25 MR = 0.10 MR = 0.04 MR = 0.01 w/o BM3D w/BM3D w/o BM3D w/BM3D w/o BM3D w/BM3D w/o BM3D w/BM3D Barbara TVAL3 24.19 24.20 21.88 22.21 18.98 18.98 11.94 11.96 NLR-CS 28.01 28.00 14.80 14.84 11.08 11.56 5.50 5.86 D-AMP 25.08 25.96 21.23 21.23 16.37 16.37 5.48 5.48 ReconNet 23.25 23.52 21.89 22.50 20.38 21.02 18.61 19.08 DR$ ^2 $-Net 25.77 25.99 22.69 22.82 20.70 21.30 18.65 19.10 MSRNet 26.69 26.91 23.04 23.06 21.01 21.28 18.60 18.90 Boats TVAL3 28.81 28.81 23.86 23.86 19.20 19.20 11.86 11.88 NLR-CS 29.11 29.27 14.82 14.86 10.76 11.21 5.38 5.72 D-AMP 29.26 29.26 21.95 21.95 16.01 16.01 5.34 5.34 ReconNet 27.30 27.35 24.15 24.10 21.36 21.62 18.49 18.83 DR$ ^2 $-Net 30.09 30.30 25.58 25.90 22.11 22.50 18.67 18.95 MSRNet 30.74 30.93 26.32 26.50 22.58 22.79 18.65 18.88 Flinstones TVAL3 24.05 24.07 18.88 18.92 14.88 14.91 9.75 9.77 NLR-CS 22.43 22.56 12.18 12.21 8.96 9.29 4.45 4.77 D-AMP 25.02 24.45 16.94 16.82 12.93 13.09 4.33 4.34 ReconNet 22.45 22.59 18.92 19.18 16.30 16.56 13.96 14.08 DR$ ^2 $-Net 26.19 26.77 21.09 21.46 16.93 17.05 14.01 14.18 MSRNet 26.67 26.89 21.72 21.81 17.28 17.40 13.83 14.10 Lena TVAL3 28.67 28.71 24.16 24.18 19.46 19.47 11.87 11.89 NLR-CS 29.39 29.67 15.30 15.33 11.61 11.99 5.95 6.27 D-AMP 28.00 27.41 22.51 22.47 16.52 16.86 5.73 5.96 ReconNet 26.54 26.53 23.83 24.47 21.28 21.82 17.87 18.05 DR$ ^2 $-Net 29.42 29.63 25.39 25.77 22.13 22.73 17.97 18.40 MSRNet 30.21 30.37 26.28 26.41 22.76 23.06 18.06 18.35 Monarch TVAL3 27.77 27.77 21.16 21.16 16.73 16.73 11.09 11.11 NLR-CS 25.91 26.06 14.59 14.67 11.62 11.97 6.38 6.71 D-AMP 26.39 26.55 19.00 19.00 14.57 14.57 6.20 6.20 ReconNet 24.31 25.06 21.10 21.51 18.19 18.32 15.39 15.49 DR$ ^2 $-Net 27.95 28.31 23.10 23.56 18.93 19.23 15.33 15.50 MSRNet 28.90 29.04 23.98 24.17 19.26 19.48 15.41 15.61 Peppers TVAL3 29.62 29.65 22.64 22.65 18.21 18.22 11.35 11.36 NLR-CS 28.89 29.25 14.93 14.99 11.39 11.80 5.77 6.10 D-AMP 29.84 28.58 21.39 21.37 16.13 16.46 5.79 5.85 ReconNet 24.77 25.16 22.15 22.67 19.56 20.00 16.82 16.96 DR$ ^2 $-Net 28.49 29.10 23.73 24.28 20.32 20.78 16.90 17.11 MSRNet 29.51 29.86 24.91 25.18 20.90 21.16 17.10 17.33 平均PSNR TVAL3 27.84 27.87 22.84 22.86 18.39 18.40 11.31 11.34 NLR-CS 28.05 28.19 14.19 14.22 10.58 10.98 5.30 5.62 D-AMP 28.17 27.67 21.14 21.09 15.49 15.67 5.19 5.23 ReconNet 25.54 25.92 22.68 23.23 19.99 20.44 17.27 17.55 DR$ ^2 $-Net 28.66 29.06 24.32 24.71 20.80 21.29 17.44 17.80 MSRNet 29.48 29.67 25.16 25.38 21.41 21.68 17.54 17.82 
下载: 导出CSV
表 2 不同算法下11幅测试图像平均SSIM
Table 2 Mean SSIM values for 11 testing images by different algorithms
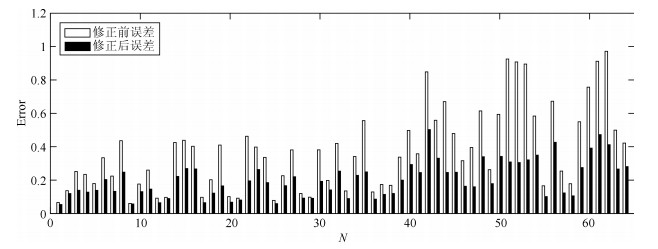
算法 MR = 0.01 MR = 0.04 MR = 0.10 MR = 0.25 ReconNet 0.4083 0.5266 0.6416 0.7579 DR$ ^2 $-Net 0.4291 0.5804 0.7174 0.8431 MSRNet 0.4535 0.6167 0.7598 0.8698
下载: 导出CSV
表 3 MSRNet重构图像修正后11幅测试图像的PSNR (dB)和SSIM
Table 3 The PSNR (dB) and SSIM of 11 test images of refined MSRNet reconstruction
图像 MR = 0.25 MR = 0.10 MR = 0.04 PSNR SSIM PSNR SSIM PSNR SSIM Monarch 29.74 0.9189 24.40 0.8078 19.62 0.6400 Parrots 30.13 0.9054 25.15 0.8240 22.06 0.7311 Barbara 27.53 0.8553 23.28 0.6630 21.39 0.5524 Boats 31.63 0.8999 26.73 0.7753 22.86 0.6355 C-man 27.17 0.8433 23.33 0.7400 20.51 0.6378 Fingerprint 28.75 0.9280 23.18 0.7777 18.81 0.5212 Flinstones 27.77 0.8529 22.14 0.7114 17.46 0.4824 Foreman 35.85 0.9297 31.71 0.8740 26.97 0.7939 House 34.15 0.8891 29.55 0.8196 25.60 0.7443 Lena 30.95 0.9019 26.68 0.7965 23.16 0.6882 Peppers 30.67 0.8898 25.43 0.7811 21.28 0.6382 平均值 30.39 0.8922 25.59 0.7791 21.79 0.6423
下载: 导出CSV
表 4 不同卷积方式在图 5的测试集中重构图像的平均PSNR (dB)
Table 4 Mean PSNR in dB for testing set in Fig. 5 by different convolution
卷积形式 MR = 0.01 MR = 0.04 MR = 0.10 MR = 0.25 普通卷积 17.50 21.23 24.79 29.05 扩张卷积 17.54 21.41 25.16 29.48
下载: 导出CSV
表 5 不同卷积方式在BSD500测试集中重构图像平均PSNR (dB)
Table 5 Mean PSNR in dB for BSD500 testing set by different convolution
算法 MR = 0.01 MR = 0.04 MR = 0.10 MR = 0.25 普通卷积 19.34 22.14 24.48 27.78 扩张卷积 19.35 22.25 24.73 27.93
下载: 导出CSV
表 6 重构一幅$ 256 \times 256 $图像的运行时间(s)
Table 6 Time (in seconds) for reconstruction a single $ 256 \times 256 $ image
算法 MR = 0.01 (CPU/GPU) MR = 0.04 (CPU/GPU) MR = 0.10 (CPU/GPU) MR = 0.25 (CPU/GPU) ReconNet 0.5363/0.0107 0.5369/0.0100 0.5366/0.0101 0.5361/0.0105 DR$ ^2 $-Net 1.2039/0.0317 1.2064/0.0317 1.2096/0.0314 1.2176/0.0326 MSRNet 0.4884/0.0121 0.5172/0.0124 0.5152/0.0117 0.5206/0.0126
下载: 导出CSV
表 7 不同算法在BSD500测试集的平均PSNR (dB)和平均SSIM
Table 7 Mean PSNR in dB and SSIM values for BSD500 testing images by different algorithms
模型 MR = 0.01 MR = 0.04 MR = 0.10 MR = 0.25 PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM ReconNet 19.17 0.4247 21.40 0.5149 23.28 0.6121 25.48 0.7241 DR$ ^2 $-Net 19.34 0.4514 21.86 0.5501 24.26 0.6603 27.56 0.7961 MSRNet 19.35 0.4541 22.25 0.5696 24.73 0.6837 27.93 0.8121
下载: 导出CSV
表 8 比较ReconNet、DR$ ^2 $-Net和MSRNet三种算法对高斯噪声的鲁棒性(图 5中11幅测试图像)
Table 8 Comparison of robustness to Gaussian noise among of ReconNet, DR$ ^2 $-Net, MSRNet (11 testing images in Fig. 5)
模型 MR = 0.25 MR = 0.10 $ \sigma $ = 0.01 $ \sigma $ = 0.05 $ \sigma $ = 0.10 $ \sigma $ = 0.25 $ \sigma $ = 0.01 $ \sigma $ = 0.05 $ \sigma $ = 0.10 $ \sigma $ = 0.25 ReconNet 25.44 23.81 20.81 14.15 22.63 21.64 19.54 14.17 DR$ ^2 $-Net 28.49 25.63 21.45 14.32 24.17 22.70 20.04 14.54 MSRNet 29.28 26.50 22.63 18.46 25.06 23.56 21.11 15.46
下载: 导出CSV
表 9 比较ReconNet、DR$ ^2 $-Net和MSRNet三种算法对高斯噪声的鲁棒性(BSD500数据集)
Table 9 Comparison of robustness to Gaussian noise among of ReconNet, DR$ ^2 $-Net, MSRNet (BSD500 dataset)
模型 MR = 0.25 MR = 0.10 $ \sigma $ = 0.01 $ \sigma $ = 0.05 $ \sigma $ = 0.10 $ \sigma $ = 0.25 $ \sigma $ = 0.01 $ \sigma $ = 0.05 $ \sigma $ = 0.10 $ \sigma $ = 0.25 ReconNet 25.38 22.03 20.72 14.03 23.22 22.06 19.85 14.51 DR$ ^2 $-Net 27.40 24.99 21.32 14.47 24.17 22.74 20.26 14.85 MSRNet 27.78 25.53 22.37 18.38 24.67 23.34 21.22 16.37
下载: 导出CSV
-
[1] Donoho D L. Compressed sensing. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306 doi: 10.1109/TIT.2006.871582 [2] Candes E J, Justin R J, Tao T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 2006, 52(2):489-509 doi: 10.1109/TIT.2005.862083 [3] Candes E J, Wakin M B. An introduction to compressive sampling. IEEE Signal Processing Magazine, 2008, 25(2):21-30 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f038caf0ee508db10a5b5fd193679bc2 [4] 任越美, 张艳宁, 李映.压缩感知及其图像处理应用研究进展与展望.自动化学报, 2014, 40(8):1563-1575 http://www.aas.net.cn/CN/abstract/abstract18426.shtmlRen Yue-Mei, Zhang Yan-Ning, Li Ying. Advances and perspective on compressed sensing and application on image processing. Acta Automatica Sinica, 2014, 40(8):1563-1575 http://www.aas.net.cn/CN/abstract/abstract18426.shtml [5] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 2007, 53(12):4655-4666 doi: 10.1109/TIT.2007.909108 [6] Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing. Applied and Computational Harmonic Analysis, 2009, 27(3):265-274 http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0805.0510 [7] Xiao Y H, Yang J F, Yuan X M. Alternating algorithms for total variation image reconstruction from random projections. Inverse Problems and Imaging, 2012, 6(3):547-563 doi: 10.3934/ipi.2012.6.547 [8] Dong W S, Shi G M, Li X, Zhang L, Wu X L. Image reconstruction with locally adaptive sparsity and nonlocal robust regularization. Signal Processing:Image Communication, 2012, 27(10):1109-1122 doi: 10.1016/j.image.2012.09.003 [9] Eldar Y C, Kuppinger P, Bolcskei H. Block-sparse signals:uncertainty relations and efficient recovery. IEEE Transactions on Signal Processing, 2010, 58(6):3042-3054 doi: 10.1109/TSP.2010.2044837 [10] 练秋生, 陈书贞.基于混合基稀疏图像表示的压缩传感图像重构.自动化学报, 2010, 36(3):385-391 http://www.aas.net.cn/CN/abstract/abstract13678.shtmlLian Qiu-Sheng, Chen Shu-Zhen. Image reconstruction for compressed sensing based on the combined sparse image representation. Acta Automatica Sinica, 2010, 36(3):385-391 http://www.aas.net.cn/CN/abstract/abstract13678.shtml [11] 沈燕飞, 李锦涛, 朱珍民, 张勇东, 代锋.基于非局部相似模型的压缩感知图像恢复算法.自动化学报, 2015, 41(2):261-272 http://www.aas.net.cn/CN/abstract/abstract18605.shtmlShen Yan-Fei, Li Jin-Tao, Zhu Zhen-Min, Zhang Yong-Dong, Dai Feng. Image reconstruction algorithm of compressed sensing based on nonlocal similarity model. Acta Automatica Sinica, 2015, 41(2):261-272 http://www.aas.net.cn/CN/abstract/abstract18605.shtml [12] Dong C, Loy C C, He K M, Tang X O. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 38(2):295-307 http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb201709007 [13] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. In:Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA:IEEE, 2015. 3431-3440 [14] Zhang K, Zuo W M, Chen Y J, Meng D Y, Zhang L. Beyond a gaussian denoiser:residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 2017, 26(7):3142-3155 doi: 10.1109/TIP.2017.2662206 [15] Mousavi A, Patel A B, Baraniuk R G. A deep learning approach to structured signal recovery. In:Proceedings of the 53rd Annual Allerton Conference on Communication, Control, and Computing. Monticello, IL, USA:IEEE, 2015. 1336-1343 [16] Kulkarni K, Lohit S, Turaga P, Kerviche R, Ashok A. ReconNet:non-iterative reconstruction of images from compressively sensed measurements. In:Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA:IEEE, 2016. 449-458 https://ieeexplore.ieee.org/document/7780424/ [17] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In:Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA:IEEE, 2016. 770-778 http://www.oalib.com/paper/4016438 [18] Yao H T, Dai F, Zhang D M, Ma Y K, Zhang S L, Zhang Y D, et al. DR2-Net:deep residual reconstruction network for image compressive sensing[Online], available:https://arxiv.org/pdf/1702.05743.pdf, July 6, 2017. [19] Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions[Online], available:https://arxiv.org/abs/1511.07122, April 30, 2016. [20] Gan L. Block compressed sensing of natural images. In:Proceedings of the 15th International Conference on Digital Signal Processing. Cardiff, UK:IEEE, 2007. 403-406 [21] Kingma D P, Ba J L. Adam:a method for stochastic optimization. In:Proceedings of the 3rd International Conference for Learning Representations. San Diego, USA:Computer Science, 2014. [22] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6):84-90 doi: 10.1145/3065386 [23] Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 2007, 16(8):2080-2095 doi: 10.1109/TIP.2007.901238 [24] Wu J S, Jiang L Y, Han X, Senhadji L, Shu H Z. Performance evaluation of wavelet scattering network in image texture classification in various color spaces. Journal of Southeast University, 2015, 31(1):46-50 http://cn.bing.com/academic/profile?id=c73d072061e32a8b8d31062f4abad153&encoded=0&v=paper_preview&mkt=zh-cn [25] Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z F, Citro C, et al. TensorFlow:large-scale machine learning on heterogeneous distributed systems[Online], available:http://tensorflow.org, September 19, 2017. [26] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. In:Proceedings of the 13th International Conference on Artificial Intelligence and Statistics. Sardinia, Italy:JMLR, 2010. 249-256 [27] Li C B, Yin W T, Jiang H, Zhang Y. An efficient augmented lagrangian method with applications to total variation minimization. Computational Optimization & Applications, 2013, 56(3):507-530 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=252968b97ae188abfb677b3e976d5e15 [28] Dong W S, Shi G M, Li X, Ma Y, Huang F. Compressive sensing via nonlocal low-rank regularization. IEEE Transactions on Image Processing, 2014, 23(8):3618-3632 doi: 10.1109/TIP.2014.2329449 [29] Metzler C A, Maleki A, Baraniuk R G. From denoising to compressed sensing. IEEE Transactions on Information Theory, 2016, 62(9):5117-5144 doi: 10.1109/TIT.2016.2556683 -
计量
- 文章访问数: 2917
- HTML全文浏览量: 885
- PDF下载量: 238
- 被引次数: 0
