融合多策略的黄金正弦黑猩猩优化算法

刘成汉; 何庆

doi:10.16383/j.aas.c210313

融合多策略的黄金正弦黑猩猩优化算法

doi: 10.16383/j.aas.c210313

刘成汉^{1, 2,},
何庆^{1, 2,}

1.
贵州大学大数据与信息工程学院贵阳 550025
2.
贵州大学公共大数据国家重点实验室贵阳 550025

基金项目: 国家自然科学基金(62166006), 贵州省科技计划项目重大专项项目([2021] 335), 公共大数据国家重点实验室开放课题(2017BDKFJJ004)资助

详细信息

作者简介:
刘成汉：贵州大学大数据与信息工程学院硕士研究生. 主要研究方向为智能优化算法, 深度学习. E-mail: lzttym@163.com

何庆：贵州大学大数据与信息工程学院教授. 主要研究方向为认知无线电, 智能算法. 本文通信作者. E-mail: qhe@gzu.edu.cn

计量
- 文章访问数: 1832
- HTML全文浏览量: 932
- PDF下载量: 253
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-12
- 录用日期: 2021-09-17
- 网络出版日期: 2021-10-13
- 刊出日期: 2023-11-22

Golden Sine Chimp Optimization Algorithm Integrating Multiple Strategies

LIU Cheng-Han^{1, 2
,},
HE Qing^{1, 2
,}

1.
College of Big Data and Information Engineering, Guizhou University, Guiyang 550025
2.
State Key Laboratory of Public Big Data, Guizhou University, Guiyang 550025

Funds: Supported by National Natural Science Foundation of China (62166006), Major Special Project of Guizhou Science and Technology Planning Project ([2021] 335), and Open Project of State Key Laboratory of Public Big Data (2017BDKFJJ004)

More Information

Author Bio:
LIU Cheng-Han　Master student at the College of Big Data and Information Engineering, Guizhou University. His research interest covers intelligent optimization algorithm and deep learning

HE Qing　Professor at the College of Big Data and Information Engineering, Guizhou University. His research interest covers cognitive radio and intelligent algorithms. Corresponding author of this paper

摘要

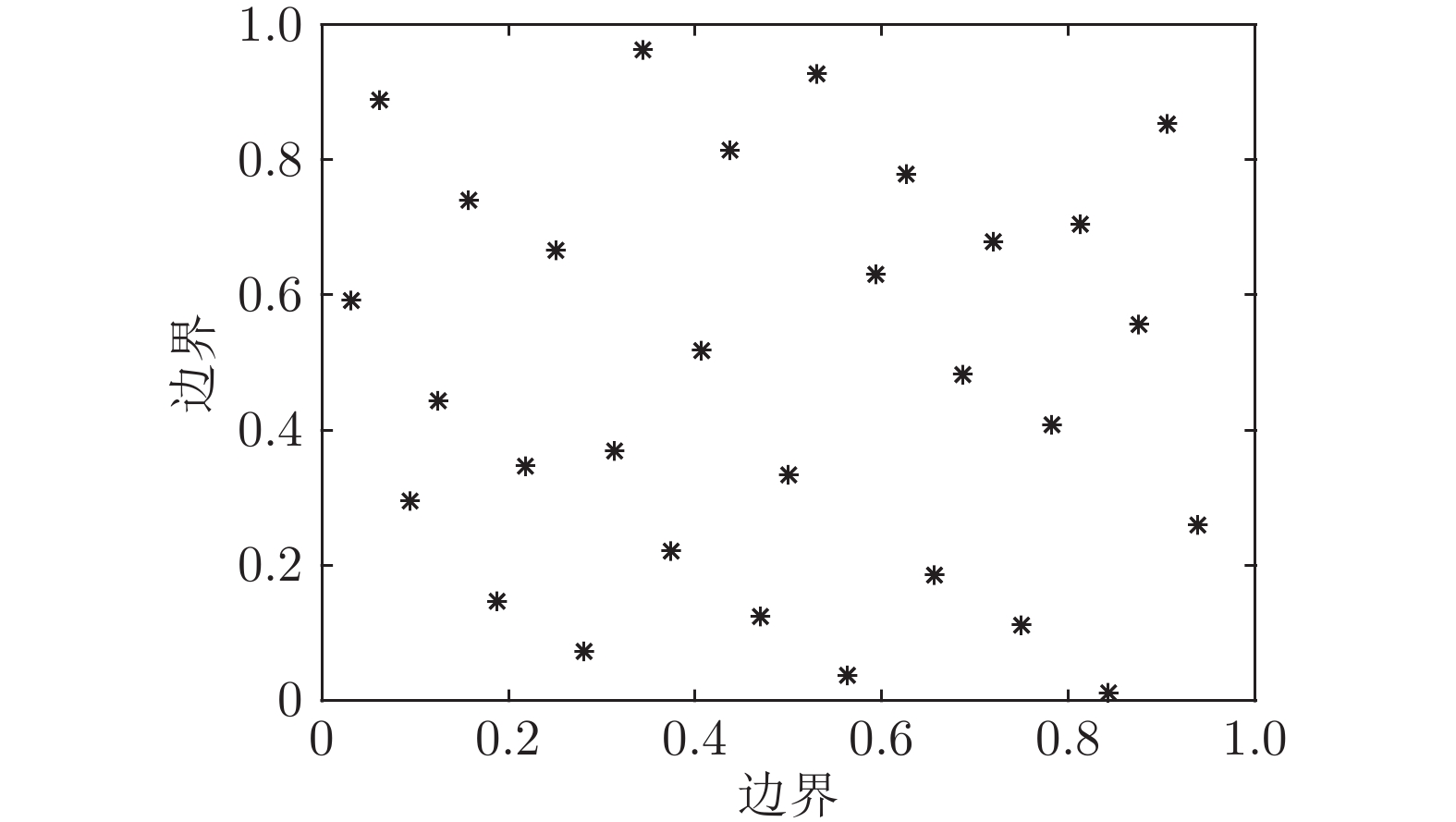
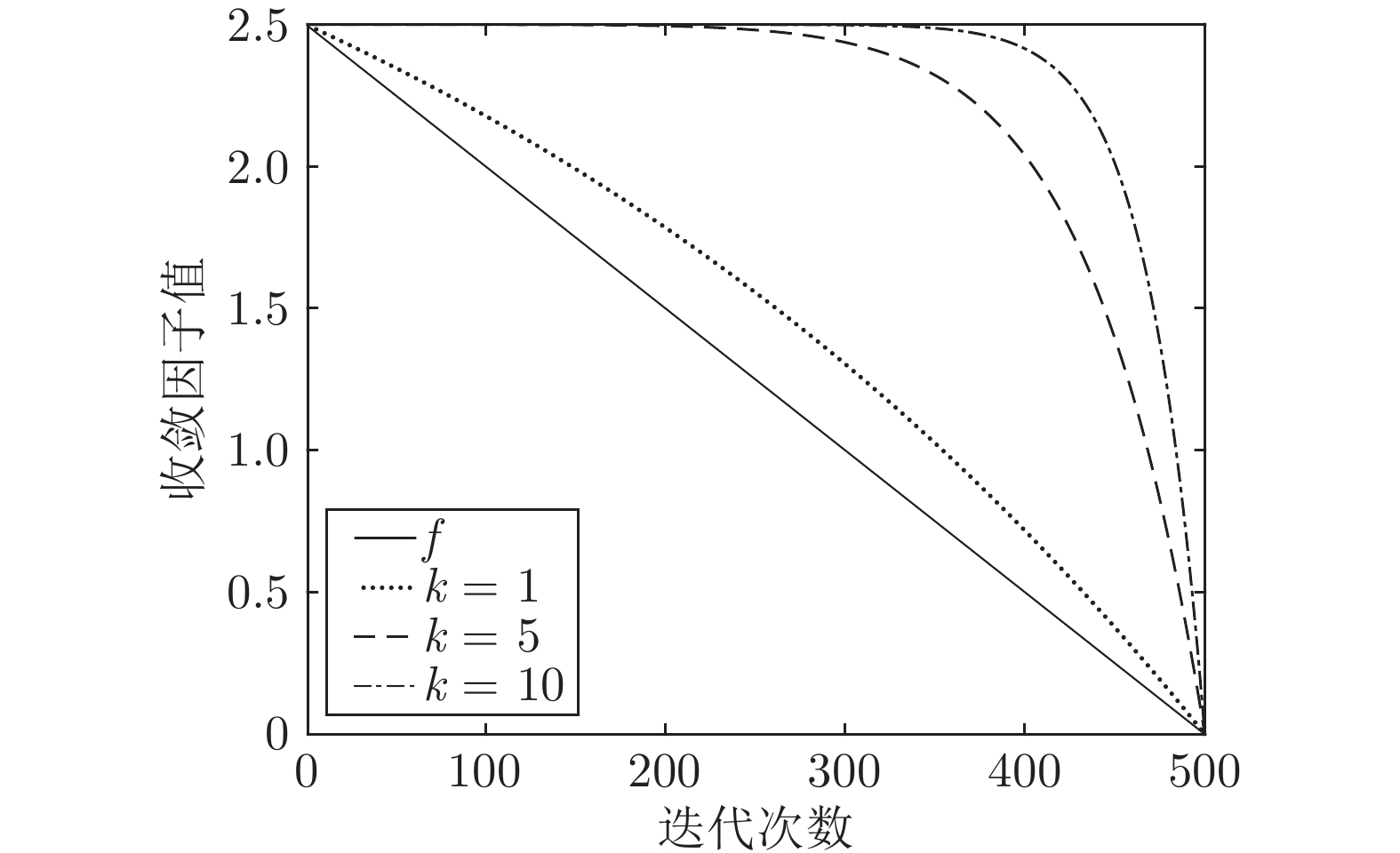
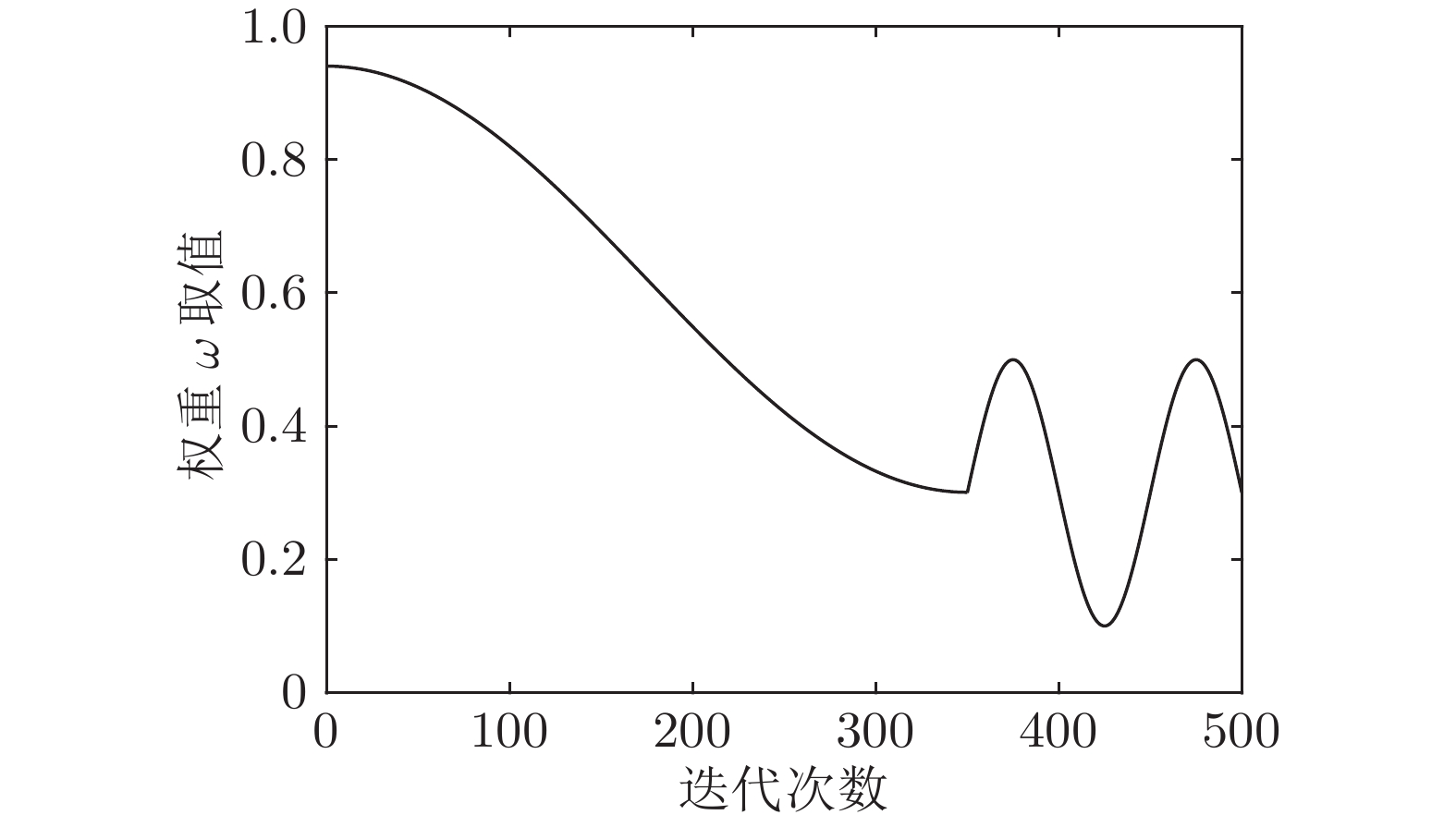
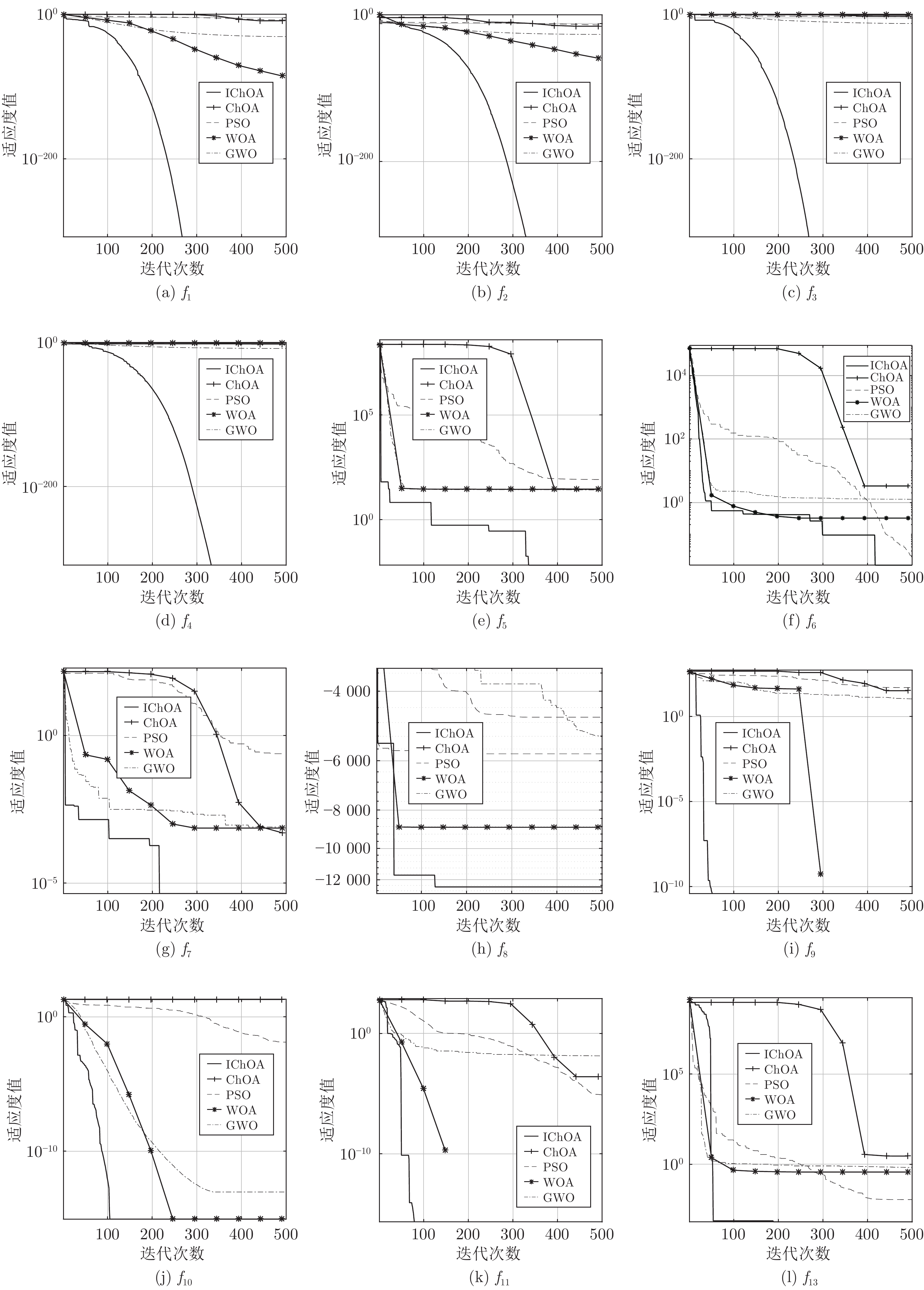
摘要: 针对黑猩猩优化算法(Chimp optimization algorithm, ChOA)存在收敛速度慢、精度低和易陷入局部最优值问题, 提出一种融合多策略的黄金正弦黑猩猩优化算法(Multi-strategy golden sine chimp optimization algorithm, IChOA). 引入Halton序列初始化种群, 提高初始化种群的多样性, 加快算法收敛, 提高收敛精度; 考虑到收敛因子和权重因子对于平衡算法勘探和开发能力的重要作用, 引入改进的非线性收敛因子和自适应权重因子, 平衡算法的搜索能力; 结合黄金正弦算法相关思想, 更新个体位置, 提高算法对局部极值的处理能力. 通过对23个基准测试函数的寻优对比分析和Wilcoxon秩和统计检验以及部分CEC2014测试函数寻优结果对比可知, 改进的算法具有更好的鲁棒性; 最后, 通过2个实际工程优化问题的实验对比分析, 进一步验证了IChOA在处理现实优化问题上的优越性.
- 黑猩猩优化算法 /
- Halton序列 /
- 非线性收敛因子 /
- 自适应权重因子 /
- 黄金正弦算法
Abstract: Chimp optimization algorithm (ChOA) has the problems of slow convergence speed, low accuracy and easy to fall into local optimal value. A multi-strategy golden sine chimp optimization algorithm (IChOA) was proposed. The Halton sequence is introduced into the algorithm to initialize the population, which improves the diversity of the initialized population, accelerates the convergence of the algorithm, and improves the convergence accuracy. Considering the important role of convergence factor and weight factor on the exploration and exploitation of the balance algorithm, the improved nonlinear convergence factor and adaptive weighting factor are introduced to balance the search ability of the algorithm. The golden sine algorithm is used to update the individual position and improve the ability of the algorithm to deal with the local extreme value. Through comparative analysis of the optimization of 23 benchmark test functions, Wilcoxon rank sum statistical test and optimization results of some CEC2014 test functions, it can be seen that the improved algorithm has better robustness. Finally, through comparative analysis of two practical engineering optimization problems, the superiority of IChOA in dealing with realistic optimization problem is further verified.
- Chimp optimization algorithm (ChOA) /
- Halton sequence /
- nonlinear convergence /
- adaptive weighting factor /
- golden sine algorithm

HTML全文

图 1 种群随机初始化个体分布图

Fig. 1 Randomly initialized population distribution map

下载: 全尺寸图片幻灯片

图 2 使用Halton序列产生的初始种群分布图

Fig. 2 Halton sequence initialized population distribution map

下载: 全尺寸图片幻灯片

图 3 收敛因子对比图

Fig. 3 Contrast diagram of convergence factors

下载: 全尺寸图片幻灯片

图 4 自适应权重因子$\omega $曲线

Fig. 4 Adaptive weighting factor$\omega $ curve

下载: 全尺寸图片幻灯片

图 5 ChOA与HChOA收敛对比图

Fig. 5 Convergence curve of ChOA and HChOA

下载: 全尺寸图片幻灯片

图 6 ChOA与WChOA收敛对比图

Fig. 6 Convergence curve of ChOA and WChOA

下载: 全尺寸图片幻灯片

图 7 ChOA与GChOA收敛对比图

Fig. 7 Convergence curve of ChOA and GChOA

下载: 全尺寸图片幻灯片

图 8 各算法500维寻优对比曲线

Fig. 8 Comparison curves of 500-dimensional optimization of each algorithm

下载: 全尺寸图片幻灯片

图 9 焊接梁模型

Fig. 9 Welding beam model

下载: 全尺寸图片幻灯片

图 10 拉力/压力弹簧优化设计问题模型

Fig. 10 The model of tension/pressure spring optimization design

下载: 全尺寸图片幻灯片

表 1 算法参数设置

Table 1 Parameter setting of algorithm

算法	参数
ChOA	$m = {{chaos} } (3, 1, 1)$
PSO	c₁ = 1.5, c₂ = 2.0, $\omega$ = 1, w_damp = 0.99
GWO	—
WOA	$b=1 $
IChOA	$m = {chaos} (3, 1, 1)$, $\delta _1=0.3,$$\delta _2=300.0, \delta _3=1.8,$ $\rho _1=0.10,\;\rho _2=0.05, \;\rho _3=0.30, \; \varepsilon=300$

下载: 导出CSV

表 2 基准测试函数介绍

Table 2 Introduction to benchmark functions

编号	函数名	定义域	维度	最优值	绝对精度误差$\varepsilon $
$f_1 $	Sphere	[−100, 100]	30	0	1.00 × 10⁻³
$f_2 $	Schwefel＇problem 2.22	[−10, 10]	30	0	1.00 × 10⁻³
$f_3 $	Schwefel＇problem 1.2	[−100, 100]	30	0	1.00 × 10⁻³
$f_4 $	Schwefel＇problem 2.21	[−100, 100]	30	0	1.00 × 10⁻³
$f_5 $	Generalized Rosenbrock＇s function	[−30, 30]	30	0	1.00 × 10⁻²
$f_6 $	Step function	[−100, 100]	30	0	1.00 × 10⁻²
$f_7 $	Quartic function	[−1.28, 1.28]	30	0	1.00 × 10⁻²
$f_8 $	Generalized Schwefel＇s problem 2.26	[−500, 500]	30	−12569.5000	1.00 × 10²
$f_9 $	Generalized Rastrigin＇s Function	[−5.12, 5.12]	30	0	1.00 × 10⁻²
$f_{10} $	Ackley＇s function	[−32, 32]	30	0	1.00 × 10⁻²
$f_{11} $	Generalized Criewank function	[−600, 600]	30	0	1.00 × 10⁻²
$f_{12} $	Generalized penalized function 1	[−50, 50]	30	0	1.00 × 10⁻²
$f_{13} $	Generalized penalized function 2	[−50, 50]	30	0	1.00 × 10⁻²
$f_{14} $	Shekell＇s foxholes function	[−65, 65]	2	1.0000	1.00 × 10⁻²
$f_{15} $	Kowalik＇s function	[−5, 5]	4	0.0003	1.00 × 10⁻²
$f_{16} $	Six-hump camel-back function	[−5, 5]	2	−1.0300	1.00 × 10⁻²
$f_{17} $	Branin function	[−5, 5]	2	0.3980	1.00 × 10⁻²
$f_{18} $	Gold stein-price function	[−2, 2]	2	3.0000	1.00 × 10⁻²
$f_{19} $	Hatman＇s function1	[0, 1]	3	−3.8600	1.00 × 10⁻²
$f_{20} $	Hatman＇s function 2	[0, 1]	6	−3.3200	1.00 × 10⁻²
$f_{21} $	Shekel＇s family 1	[0, 10]	4	−10.0000	1.00 × 10⁻²
$f_{22}$	Shekel＇s family 2	[0, 10]	4	−10.0000	1.00 × 10⁻²
$f_{23} $	Shekel＇s family 3	[0, 10]	4	−10.0000	1.00 × 10⁻²

下载: 导出CSV

表 3 各算法寻优结果对比(30维)

Table 3 Comparison of optimization results of each algorithm (30 dim)

函数	ChOA		PSO		GWO		SChOA		IChOA
函数	平均值	标准差	平均值	标准差	平均值	标准差	平均值	标准差	平均值	标准差
$f_{1} $	1.34 × 10⁻⁵	1.19 × 10⁻²⁰	1.40 × 10⁻⁴	2.11 × 10⁻⁴	5.95 × 10⁻²⁸	6.85 × 10⁻²⁸	5.66 × 10⁻³³	5.68 × 10³	0	0
$f_{2} $	1.42 × 10⁻⁵	8.55 × 10⁻²¹	4.21 × 10⁻²	4.54 × 10⁻²	7.95 × 10⁻¹⁷	4.97 × 10⁻¹⁷	1.72 × 10⁻²⁰	1.91 × 10¹⁰	0	0
$f_{3} $	6.31 × 10⁰	1.40 × 10⁻¹⁷	7.01 × 10¹	2.21 × 10¹	2.83 × 10⁻⁵	1.12 × 10⁻⁴	6.19 × 10⁻⁸	2.25 × 10⁴	0	0
$f_{4} $	2.75 × 10⁻²	5.95 × 10⁻²⁸	1.08 × 10⁰	3.17 × 10⁻¹	5.69 × 10⁻⁷	5.55 × 10⁻⁷	2.75 × 10⁻¹⁰	1.26 × 10⁰	0	0
$f_{5} $	2.87 × 10¹	2.51 × 10⁻¹⁴	9.67 × 10¹	6.01 × 10¹	2.70 × 10¹	8.26 × 10⁻¹	2.85 × 10²	1.00 × 10⁷	3.13 × 10⁻⁴	5.26 × 10⁻¹⁷
$f_{6} $	3.72 × 10⁰	4.48 × 10⁻¹⁵	1.10 × 10⁻⁴	8.28 × 10⁻⁵	7.64 × 10⁻¹	3.58 × 10⁻¹	3.01 × 10⁰	5.62 × 10³	6.51 × 10⁻³	3.25 × 10⁻⁴
$f_{7} $	1.72 × 10⁻³	1.09 × 10⁻¹⁸	1.22 × 10⁻¹	4.49 × 10⁻²	1.72 × 10⁻³	7.51 × 10⁻⁴	1.00 × 10⁻³	5.77 × 10¹	7.81 × 10⁻⁷	1.02 × 10⁻¹²
$f_{8} $	−5.65 × 10³	2.75 × 10⁻¹²	−4.84 × 10³	1.15 × 10³	−6.08 × 10³	1.02 × 10³	−9.87 × 10³	1.80 × 10²	−1.26 × 10⁴	1.83 × 10⁻¹¹
$f_{9} $	1.41 × 10¹	0	4.67 × 10¹	1.16 × 10¹	3.22 × 10⁰	4.16 × 10⁰	0	7.77 × 10¹	0	0
$f_{10} $	1.96 × 10¹	1.79 × 10⁻¹⁴	2.76 × 10⁻¹	5.09 × 10⁻¹	1.05 × 10⁻¹³	2.39 × 10⁻¹⁴	1.50 × 10⁻¹⁴	1.76 × 10¹	8.88 × 10⁻¹⁶	0
$f_{11} $	4.79 × 10⁻²	7.00 × 10⁻¹⁷	9.21 × 10⁻³	7.74 × 10⁻³	5.14 × 10⁻³	9.98 × 10⁻³	0	8.30 × 10¹	0	0
$f_{12} $	3.98 × 10⁻¹	5.60 × 10⁻¹⁷	6.92 × 10⁻³	1.19 × 10⁻²	5.99 × 10⁻²	9.78 × 10⁻²	1.62 × 10⁻¹	3.31 × 10⁷	6.46 × 10⁻⁴	4.39 × 10⁻¹⁸
$f_{13} $	2.82 × 10⁰	1.76 × 10⁻¹⁵	6.68 × 10⁻³	8.91 × 10⁻³	6.27 × 10⁻¹	3.06 × 10⁻¹	6.76 × 10⁻¹	5.16 × 10⁷	2.97 × 10⁻⁵	4.56 × 10⁻¹⁶
$f_{14} $	1.00 × 10⁰	1.12 × 10⁻¹⁵	3.63 × 10⁰	2.50 × 10⁰	5.09 × 10⁰	4.34 × 10⁰	1.00 × 10⁰	1.04 × 10¹	0.99 × 10⁰	4.48 × 10⁻¹⁶
$f_{15} $	1.36 × 10⁻³	4.39 × 10⁻¹⁹	5.80 × 10⁻⁴	2.21 × 10⁻⁴	5.73 × 10⁻³	8.98 × 10⁻³	6.80 × 10⁻⁴	1.70 × 10⁻³	2.30 × 10⁻⁴	5.46 × 10⁻¹⁹
$f_{16} $	−1.03 × 10⁰	6.72 × 10⁻¹⁵	−1.03 × 10⁰	6.25 × 10⁻¹⁶	−1.03 × 10⁰	2.42 × 10⁻⁸	−1.03 × 10⁰	2.21 × 10⁻¹	−1.03 × 10⁰	5.60 × 10⁻¹⁶
$f_{17} $	3.98 × 10⁻¹	3.36 × 10⁻¹⁶	3.98 × 10⁻¹	0	3.98 × 10⁻¹	0	3.99 × 10⁻¹	4.90 × 10⁻³	3.99 × 10⁻¹	8.98 × 10⁻¹⁶
$f_{18} $	3.00 × 10⁰	0	3.18 × 10⁰	1.33 × 10⁻¹⁵	5.70 × 10⁰	1.47 × 10¹	3.00 × 10⁰	1.92 × 10⁻¹	3.00 × 10⁰	0
$f_{19} $	−3.85 × 10⁰	2.69 × 10⁻¹⁵	−3.86 × 10⁰	2.58 × 10⁻¹⁵	−3.86 × 10⁰	2.17 × 10⁻³	−3.86 × 10⁰	9.16 × 10⁻²	−3.72 × 10⁰	1.34 × 10⁻¹⁸
$f_{20} $	−1.92 × 10⁰	1.12 × 10⁻¹⁵	−3.26 × 10⁰	6.05 × 10⁻²	−3.23 × 10⁰	8.43 × 10⁻²	−3.32 × 10⁰	1.24 × 10⁻¹	−2.90 × 10⁰	5.23 × 10⁻¹⁵
$f_{21} $	−4.92 × 10⁰	2.69 × 10⁻¹⁵	−6.87 × 10⁰	3.01 × 10⁰	−8.80 × 10⁰	2.20 × 10⁰	−1.01 × 10¹	3.34 × 10⁻¹	−1.01 × 10¹	2.38 × 10⁻¹⁵
$f_{22} $	−4.99 × 10⁰	2.69 × 10⁻¹⁵	−8.46 × 10⁰	3.08 × 10⁰	−10.22 × 10⁰	9.70 × 10⁻¹	−5.18 × 10⁰	5.74 × 10⁻²	−9.78 × 10⁰	8.79 × 10⁻¹⁵
$f_{23} $	−5.02 × 10⁰	4.48 × 10⁻¹⁶	−8.95 × 10⁰	1.78 × 10⁰	−9.90 × 10⁰	1.96 × 10⁰	−1.05 × 10¹	4.95 × 10⁻²	−9.93 × 10⁰	8.97 × 10⁻¹⁶

下载: 导出CSV

表 4 Wilcoxon秩和检验结果

Table 4 Wilcoxon rank sum test results

编号	PSO ($p_{1} $)	GWO ($p_{2} $)	WOA ($p_{3} $)	ChOA ($p_{4} $)	GChOA ($p_{5} $)
$f_{1} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰
$f_{2} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.25 × 10⁻²⁰
$f_{3} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰
$f_{4} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰
$f_{5} $	1.01 × 10⁻¹⁷	2.47 × 10⁻¹⁷	1.04 × 10⁻¹⁵	2.29 × 10⁻¹⁵	7.96 × 10⁻¹⁸
$f_{6} $	7.06 × 10⁻¹⁸	1.28 × 10⁻¹⁷	1.38 × 10⁻¹⁵	2.13 × 10⁻¹⁶	7.06 × 10⁻¹⁸
$f_{7} $	4.20 × 10⁻¹⁷	7.06 × 10⁻¹⁸	6.88 × 10⁻¹⁴	1.36 × 10⁻¹⁷	1.27 × 10⁻¹⁶
$f_{8} $	7.06 × 10⁻¹⁸	7.06 × 10⁻¹⁸	2.21 × 10⁻¹⁰	7.06 × 10⁻¹⁸	7.06 × 10⁻¹⁸
$f_{9} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	NaN	1.17 × 10⁻¹⁹	3.31 × 10⁻²⁰
$f_{10} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	2.39 × 10⁻¹⁶	2.91 × 10⁻²⁰	2.62 × 10⁻²³
$f_{11} $	3.31 × 10⁻²⁰	3.31 × 10⁻²⁰	3.27 × 10⁻¹	2.50 × 10⁻⁴	3.31 × 10⁻²⁰
$f_{12} $	7.06 × 10⁻¹⁸	9.37 × 10⁻¹¹	1.83 × 10⁻¹⁷	7.96 × 10⁻¹⁸	7.06 × 10⁻¹⁸
+/=/−	12/0/0	12/0/0	10/1/1	12/0/0	12/0/0

下载: 导出CSV

表 5 部分CEC2014函数介绍

Table 5 Introduction of part CEC2014 function

函数	维度	特征	定义域	最佳值
CEC03	30	单峰	[−100, 100]	300
CEC05	30	多峰	[−100, 100]	500
CEC06	30	多峰	[−100, 100]	600
CEC16	30	多峰	[−100, 100]	1600
CEC19	30	混合	[−100, 100]	1900
CEC22	30	混合	[−100, 100]	2200
CEC25	30	复合	[−100, 100]	2500
CEC27	30	复合	[−100, 100]	2700

下载: 导出CSV

表 6 CEC2014函数优化对比

Table 6 CEC2014 function optimization comparison

函数	PSO		SCA		L-SHADE		HChOA		GChOA		IChOA
函数	平均值	标准差	平均值	标准差	平均值	标准差	平均值	标准差	平均值	标准差	平均值	标准差
CEC03	4.87 × 10¹	6.61 × 10¹	8.83 × 10⁰	1.36 × 10⁰	0	0	7.78 × 10⁴	7.44 × 10³	7.54 × 10⁴	6.58 × 10³	7.35 × 10⁴	6.23 × 10³
CEC05	2.09 × 10¹	8.52 × 10⁻²	2.21 × 10⁰	2.72 × 10⁰	2.01 × 10¹	1.70 × 10⁻²	5.22 × 10²	6.67 × 10⁻²	5.26 × 10²	4.21 × 10⁻²	5.20 × 10²	1.02 × 10⁻²
CEC06	1.08 × 10¹	2.53 × 10⁰	6.63 × 10¹	3.74 × 10¹	1.67 × 10⁻²	9.17 × 10⁻²	6.33 × 10²	2.42 × 10⁰	6.33 × 10⁻⁵	2.42 × 10⁰	6.31 × 10²	2.39 × 10⁰
CEC16	1.13 × 10¹	7.05 × 10⁻¹	2.27 × 10¹	1.66 × 10⁻¹	8.48 × 10⁰	2.97 × 10⁻¹	1.62 × 10³	2.81 × 10⁻¹	1.61 × 10³	1.88 × 10⁻¹	1.61 × 10³	1.24 × 10⁻¹
CEC19	7.76 × 10⁰	1.87 × 10⁰	2.88 × 10²	2.99 × 10¹	3.59 × 10⁰	7.22 × 10⁻¹	2.56 × 10³	2.46 × 10⁰	1.76 × 10³	2.39 × 10⁰	2.32 × 10³	1.96 × 10⁰
CEC22	2.31 × 10²	1.04 × 10²	2.43 × 10¹	3.03 × 10¹	3.69 × 10¹	3.36 × 10¹	3.57 × 10³	9.65 × 10¹	4.21 × 10³	1.48 × 10²	3.56 × 10³	7.48 × 10¹
CEC25	2.09 × 10²	1.65 × 10⁰	2.69 × 10²	2.71 × 10¹	2.03 × 10²	4.97 × 10⁻²	2.71 × 10³	9.49 × 10⁰	2.71 × 10³	3.21 × 10⁰	2.70 × 10³	0
CEC27	5.36 × 10²	8.15 × 10³	2.08 × 10²	1.89 × 10¹	3.00 × 10²	1.34 × 10⁻¹³	2.93 × 10³	5.36 × 10⁰	2.91 × 10³	8.12 × 10⁰	2.90 × 10³	0

下载: 导出CSV

表 7 基准函数寻优平均时间及成功率对比

Table 7 Comparison of average time and success rate for optimization of benchmark function

函数	ChOA			HChOA			WChOA			GChOA			IChOA
函数	平均值	标准差	成功率 (%)	平均值	标准差	成功率 (%)	平均值	标准差	成功率 (%)	平均值	标准差	成功率 (%)	平均值	标准差	成功率 (%)
f₁	1.9732	0.0136	100	1.9824	0.0088	100	1.9302	0.0155	100	1.4113	0.0181	100	1.3916	0.0101	100
f₂	1.9546	0.0101	100	1.9841	0.0181	100	1.7962	0.0063	100	1.4176	0.0101	100	1.4086	0.0081	100
f₃	2.2999	0.0083	0	2.2988	0.0077	100	2.0616	0.0906	100	2.1272	0.0128	100	2.1150	0.0275	100
f₄	2.0456	0.0107	0	1.9884	0.0309	100	1.9955	0.0676	100	1.4381	0.0330	100	1.4208	0.0446	100
f₅	2.0696	0.0663	0	2.0691	0.0649	0	1.9966	0.0326	33.3	1.4670	0.0530	96.6	1.4574	0.0244	100
f₆	2.0127	0.0435	0	1.9617	0.0107	36.6	1.9604	0.0138	16.6	1.4122	0.0111	43.3	1.4006	0.0121	90.0
f₇	2.0567	0.0089	100	2.0364	0.0190	100	2.0520	0.0147	100	1.5407	0.0070	100	1.5356	0.0098	100
f₈	2.0246	0.0127	0	2.0195	0.0310	0	1.9784	0.0294	0	1.4638	0.0086	73.3	1.4625	0.0132	83.3
f₉	2.0138	0.0343	0	2.0203	0.0112	96.6	1.9855	0.0096	100	1.4316	0.0184	100	1.4169	0.0141	100
f₁₀	2.0011	0.0113	0	2.0045	0.0143	73.3	1.9999	0.0086	100	1.4521	0.0113	100	1.4395	0.0089	100
f₁₁	2.0293	0.0081	63.3	2.0301	0.0144	100	2.0155	0.0095	100	1.4776	0.0119	100	1.4735	0.0116	100
f₁₂	2.2040	0.0114	0	2.1930	0.0142	33.3	2.1697	0.0169	86.6	1.8354	0.0110	43.3	1.8422	0.0530	100
f₁₃	2.1873	0.0112	0	2.1792	0.0115	36.6	2.1811	0.0184	56.6	1.8180	0.0140	66.6	1.8140	0.0084	100
f₁₄	0.7893	0.0090	100	0.7916	0.0068	100	0.7898	0.0073	100	1.3830	0.0100	100	1.3571	0.0064	100
f₁₅	0.3131	0.0039	0	0.3141	0.0034	50.0	0.3174	0.0024	63.3	0.2792	0.0027	90.0	0.2788	0.0024	96.6
f₁₆	0.1730	0.0038	100	0.1743	0.0034	100	0.1728	0.0037	100	0.1647	0.0037	100	0.1647	0.0013	100
f₁₇	0.1690	0.0012	100	0.1709	0.0043	100	0.1689	0.0013	100	0.1556	0.0061	100	0.1524	0.0022	100
f₁₈	0.1673	0.0025	100	0.1699	0.0035	100	0.1689	0.0021	100	0.1516	0.0012	100	0.1510	0.0020	100
f₁₉	0.2804	0.0045	100	0.2847	0.0031	100	0.2849	0.0019	100	0.3021	0.0064	100	0.2580	0.0017	100
f₂₀	0.4751	0.0042	46.6	0.4737	0.0024	70.0	0.4724	0.0028	63.3	0.4304	0.0053	63.3	0.4278	0.0033	76.6
f₂₁	0.4046	0.0251	16.6	0.4068	0.0035	20.0	0.4012	0.0028	70.0	0.4581	0.0029	76.6	0.4035	0.0055	83.3
f₂₂	0.4447	0.0043	0	0.4458	0.0030	36.6	0.4403	0.0050	53.3	0.5391	0.0048	73.3	0.4349	0.0051	80.0
f₂₃	0.5087	0.0029	0	0.5089	0.0036	43.3	0.5080	0.0021	36.6	0.6610	0.0034	76.6	0.6347	0.0039	86.6

下载: 导出CSV

表 8 焊接梁设计问题结果对比

Table 8 Comparative results of welding beam design problems

算法	h	l	t	b	平均值
GA	0.2455	6.1986	8.1264	0.2247	2.4412
PSO	0.2027	3.4705	9.0366	0.2057	1.7249
WOA	0.2024	3.4772	9.0435	0.2189	1.7299
GWO	0.2022	3.4893	9.0541	0.2155	1.7265
RO	0.2036	3.5284	9.0042	0.2072	1.7353
MVO	0.2054	3.4731	9.0445	0.2056	1.7246
HSSAHHO	0.2057	3.4705	9.0367	0.2057	1.7248
ChOA	0.2214	3.5358	8.9115	0.2127	1.7737
SChOA	0.2057	3.4705	9.0306	0.2056	1.7229
IChOA	0.2038	3.4713	9.0300	0.2060	1.7228

下载: 导出CSV

表 9 拉力/压力弹簧优化设计问题结果对比

Table 9 Comparison of tension/compression spring design

算法	d	D	P	平均值
GA	0.0528	0.3523	11.5980	0.01250
PSO	0.0500	0.3174	14.0278	0.01270
WOA	0.5119	0.3452	12.0052	0.01260
GWO	0.5156	0.3562	11.5560	0.01250
RO	0.0413	0.3490	11.7620	0.01260
MFO	0.0510	0.3641	10.8684	0.01260
HSSAHHO	0.0514	0.3535	11.3546	0.01240
ChOA	0.0500	0.3159	14.2629	0.01280
SChOA	0.0524	0.3489	10.6543	0.01187
IChOA	0.0510	0.3374	11.5068	0.01185

下载: 导出CSV

参考文献(27)

[1]	何东晓, 周栩, 王佐, 等. 复杂网络社区挖掘—基于聚类融合的遗传算法. 自动化学报, 2010, 36(8): 1160--1170. doi: 10.3724/SP.J.1004.2010.01160 He D X, Zhou X, Wang Z, et al. Complex Network Community Mining: Genetic Algorithm Based on Clustering Fusion. Acta Automatica Sinica, 2010, 36(8): 1160--1170. doi: 10.3724/SP.J.1004.2010.01160
[2]	Parsopoulos K E, Vrahatis M N. Particle swarm optimization method for constrained optimization problems. Intelligent Technologies —— Theory and Application: New Trends in Intelligent Technologies, 2002, 76(1): 214−220.
[3]	龙文, 伍铁斌, 唐明珠, 徐明, 蔡绍洪. 基于透镜成像学习策略的灰狼优化算法. 自动化学报, 2020, 46(10): 2148--2164. Long W, Wu T B, Tang M Z, et al. A Grey Wolf Optimization Algorithm Based on Lens Imaging Learning Strategy. Acta Automatica Sinica, 2020, 46(10): 2148-2164.
[4]	Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Computing, 2019, 23(3): 715--734. doi: 10.1007/s00500-018-3102-4
[5]	Tharwat A, Elhoseny M, Hassanien A E, et al. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Cluster Computing, 2019, 22(2): 4745--4766..
[6]	Guha D, Roy P K, Banerjee S. Load frequency control of interconnected power system using grey wolf optimization. Swarm and Evolutionary Computation, 2016, 27: 97--115. doi: 10.1016/j.swevo.2015.10.004
[7]	Khishe M, Mosavi M R. Chimp optimization algorithm. Expert systems with applications, 2020, 149: 113338. doi: 10.1016/j.eswa.2020.113338
[8]	Lu C, Liang G, Jin Y. Grey wolf optimizer with cellular topological structure. Expert Systems with Applications, 2018, 107: 89--114. doi: 10.1016/j.eswa.2018.04.012
[9]	王坚浩, 张亮, 史超. 基于混沌搜索策略的鲸鱼优化算法[J]. 控制与决策, 2019, 34(9): 1893--1900. Wang J H, Zhang L, Shi C. Whale optimization algorithm based on chaotic search strategy. Control and Decision, 2019, 34(9): 1893--1900.
[10]	宁杰琼, 何庆. 混合策略改进的蝴蝶优化算法. 计算机应用研究, 2021, 38(06): 1718-1723+1738. Ning J Q, He Q. Butterfly optimization algorithm improved by hybrid strategy. Application Research of Computers, 2021, 38(06): 1718--1723+1738.
[11]	王秋萍, 王梦娜, 王晓峰. 改进收敛因子和比例权重的灰狼优化算法. 计算机工程与应用, 2019, 55(21): 60--65. doi: 10.3778/j.issn.1002-8331.1808-0117 Wang Q P, Wang M N, Wang X F. Grey wolf optimization algorithm with improved convergence factor and proportional weight. Computer Engineering and Applications, 2019, 55(21): 60--65. doi: 10.3778/j.issn.1002-8331.1808-0117
[12]	Ewees A A, Abd Elaziz M, Houssein E H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Systems with Applications, 201 8, 112: 156--172. doi: 10.1016/j.eswa.2018.06.023
[13]	Dinkar S K, Deep K. Opposition based Laplacian ant lion optimizer. Journal of computational science, 2017, 23: 71--90. doi: 10.1016/j.jocs.2017.10.007
[14]	吕鑫, 慕晓冬, 张钧, 王震. 混沌麻雀搜索优化算法. 北京航空航天大学学报. 2020, 16(05): 1-10. Lu X, Mu X D, Zhang J, Wang Z. Chaos Sparrow Search Optimization Algorithm. Journal of Beijing University of Aeronautics and Astronautics. 2020, 16(05): 1--10.
[15]	Sayed S A E F, Nabil E, Badr A. A binary clonal flower pollination algorithm for feature selection. Pattern Recognition Letters, 2016, 77: 21--27. doi: 10.1016/j.patrec.2016.03.014
[16]	Bangyal W H, Batool H, Ahmed J, et al. An improved particle swarm optimization algorithm with chi-square mutation strategy. International Journal of Advanced Computer Science and Applications, 2019, 10(3): 481-491.
[17]	Tanyildizi E, Demir G. Golden sine algorithm: A novel math-inspired algorithm. Advances in Electrical and Computer Engineering, 2017, 17(2): 71--78. doi: 10.4316/AECE.2017.02010
[18]	邢燕祯, 王东辉. 基于模糊控制的权重决策灰狼优化算法. 计算机系统应用, 2018, 27(10): 202--208. Xing Y Z, Wang D H. Weight decision gray wolf optimization algorithm based on fuzzy control. Computer Systems & Applications, 2018, 27(10): 202--208.
[19]	郭文艳, 王远, 戴芳, 等. 基于精英混沌搜索策略的交替正余弦算法. 控制与决策, 2019, 34(8): 1654--1662. Guo W Y, Wang Y, Dai F, et al. Alternating Sine and Cosine Algorithm Based on Elite Chaotic Search Strategy. Control and Decision, 2019, 34(8): 1654--1662.
[20]	汪超, 王丙柱, 岑豫皖, 谢能刚. 基于多样性全局最优引导和反向学习的离子运动算法. 控制与决策, 2020, 35(7): 1584−1596. Wang Chao, Wang Bing-Zhu, Cen Yu-Wan, Xie Neng-Gang. Ion motion algorithm based on diversity global optimal guidance and reverse learning Control and Decision, 2020, 35(7): 1584−1596.
[21]	Kaur M, Kaur R, Singh N, et al. SChoA: an newly fusion of sine and cosine with chimp optimization algorithm for HLS of datapaths in digital filters and engineering applications. Engineering with Computers, 2021, 42, 1--29.
[22]	Zhang X M, Wang X, Kang Q. Improved grey wolf optimizer and its application to high dimension alfunction and FCM optimization. Control and Decision, 2019, 10(8): 1--10.
[23]	Liang J J, Qu B Y, Suganthan P N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-parameter Numerical Optimization, Technical Report, Computational Intelligence Laboratory, Zhengzhou University, China, 2013.
[24]	Xu G P, Cui Q L, Shi X H, et al. Particle swarm optimization based on dimensional learning strategy. Swarm and Evolutionary Computation, 2019, 45: 33--51. doi: 10.1016/j.swevo.2018.12.009
[25]	Chen H L, Wang M J, Zhao X H. A multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Applied Mathematics and Computation, 2020, 369: 124872. doi: 10.1016/j.amc.2019.124872
[26]	Tanabe R, Fukunaga A S. Improving the search performance of SHADE using linear population size reduction. In: Proceedings of the IEEE Congress on Evolutionary Computation. Beijing, China: IEEE, 2014. 1658−1665
[27]	傅文渊. 具有万有引力加速机理的布谷鸟搜索算法. 软件学报, 2021, 32(05): 1480--1494. Fu W Y. Cuckoo Search Algorithm with Gravity Acceleration Mechanism. Journal of Software, 2021, 32(05): 1480--1494.