Graph Band-limited Signals Reconstruction Method Based Graph Spectral Domain Shifting
-
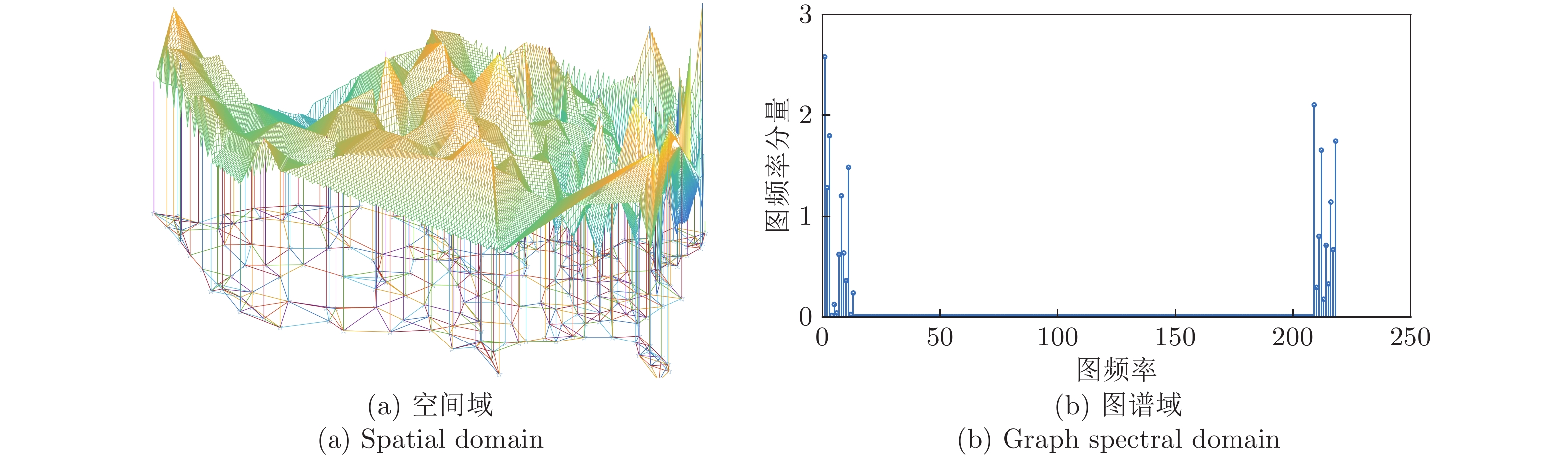
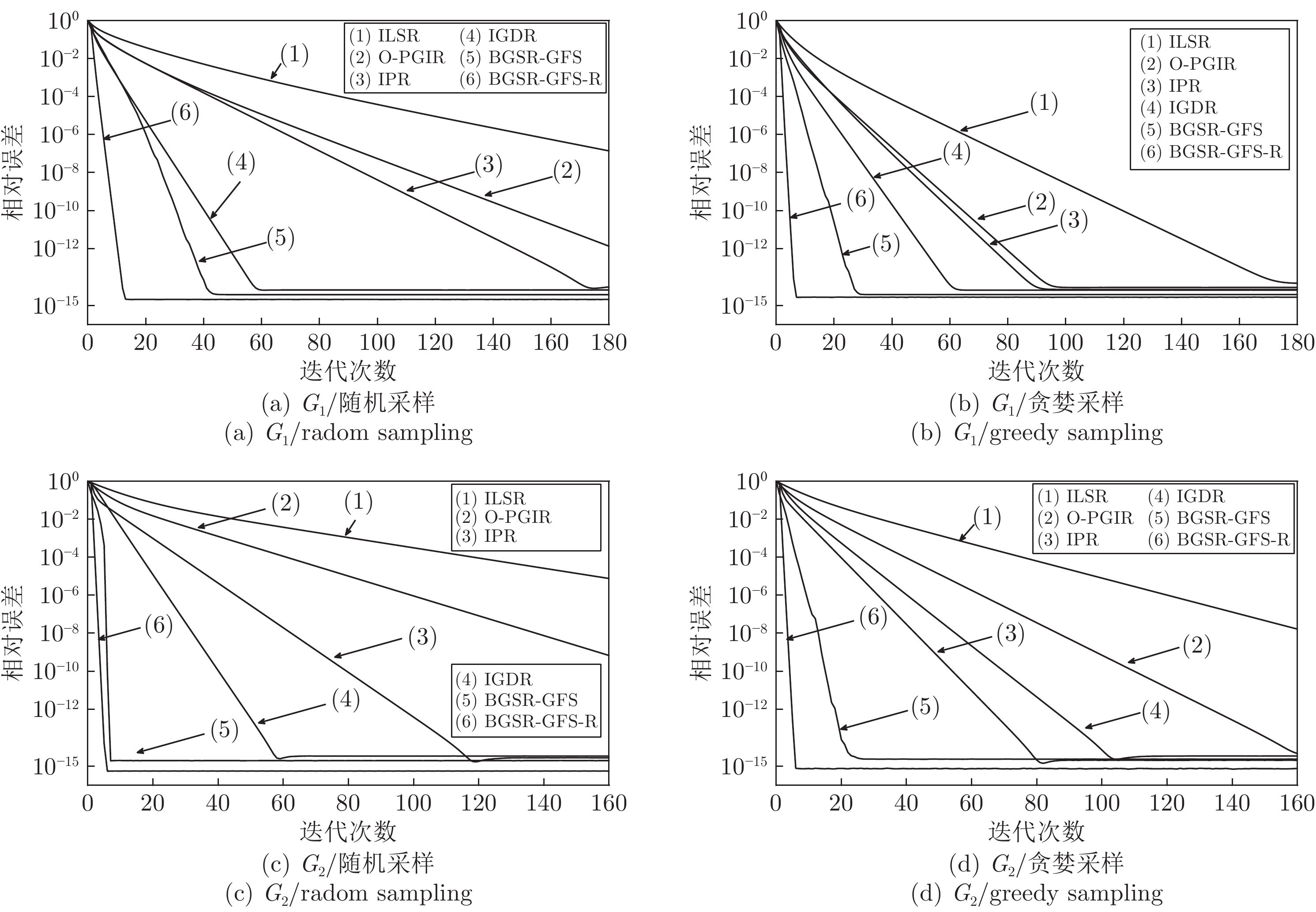
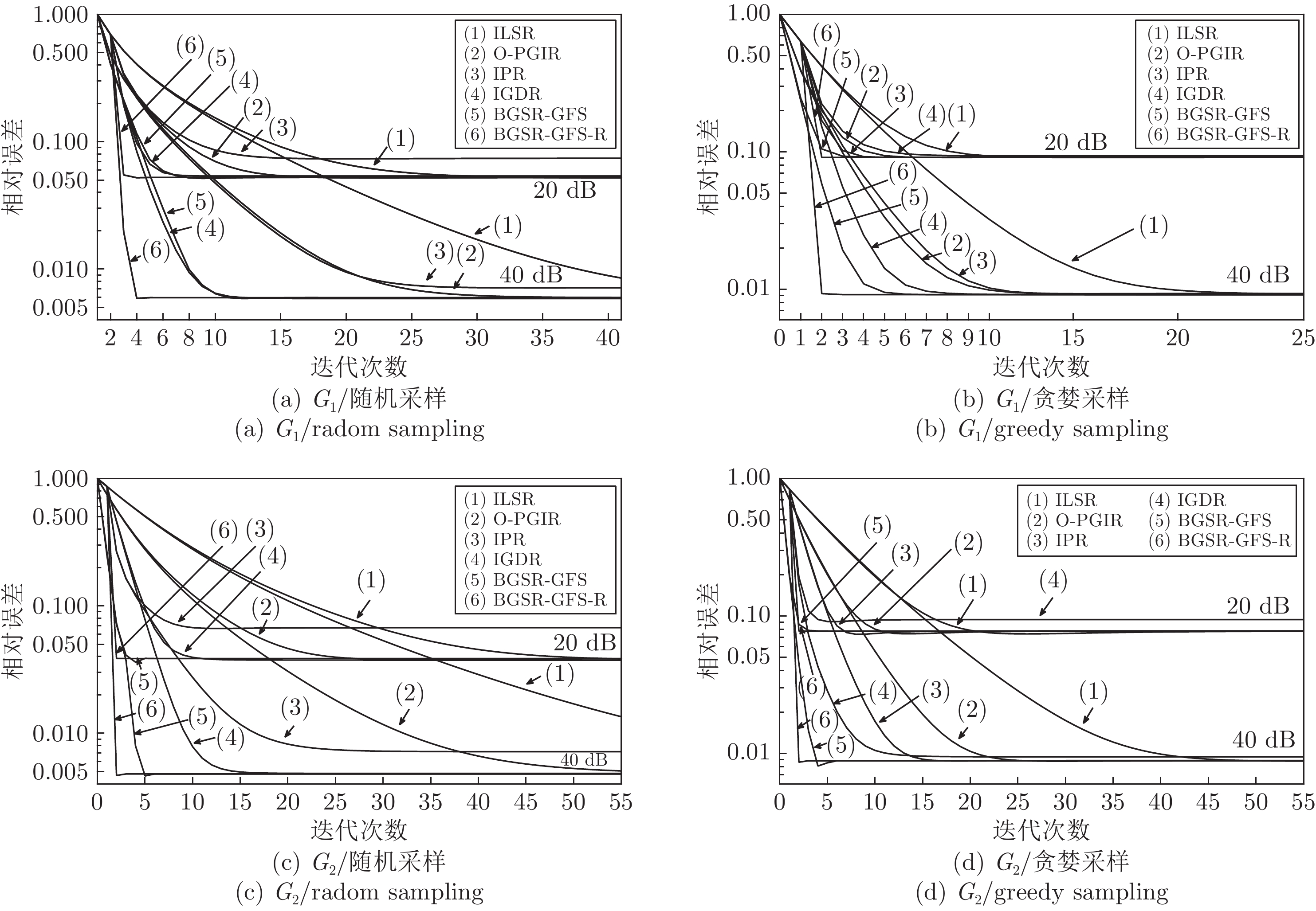
摘要: 针对带限图信号的重构问题, 本文提出了基于图谱域移位的带限图信号重构模型, 该模型将图带限分量的恒等不变特性建模为最小二乘问题. 基于所提出的重构模型, 本文设计了基于谱移位的重构算法和基于残差谱移位的重构算法. 相比于其他重构算法, 两种新算法提升了迭代效率和重构精度. 此外, 本文算法还适用于分段带限图信号的重构问题, 并且具有良好的迭代效率和重构精度.通过实验仿真表明, 相比于目前其他的带限图信号重构算法, 新算法的迭代效率提升约70%和重构精度提升约60%.Abstract: Aiming at the problem of graph band-limited signals reconstruction, a novel reconstruction model based shift strategy in graph spectral domain is proposed in this paper, and it models the identity invariance of graph spectral band-limited components as a least-square problem. For solving the established reconstruction model, two novel reconstruction methods are proposed based on spectral shift operator and residual spectral shift operator. Compared with other methods, the novel methods improve iteration efficiency and reconstruction accuracy. Besides, the novel methods are suitable for the problem of separate band-limited graph signals reconstruction and have good performances. The simulation shows that compared with other reconstruction methods of band-limited graph signals, the novel methods improve about seventy percent in iterative efficiency and sixty percent of reconstruction accuracy.
-
Key words:
- Graph signal processing /
- signal reconstruction /
- graph spectral theory /
- shift operator
-
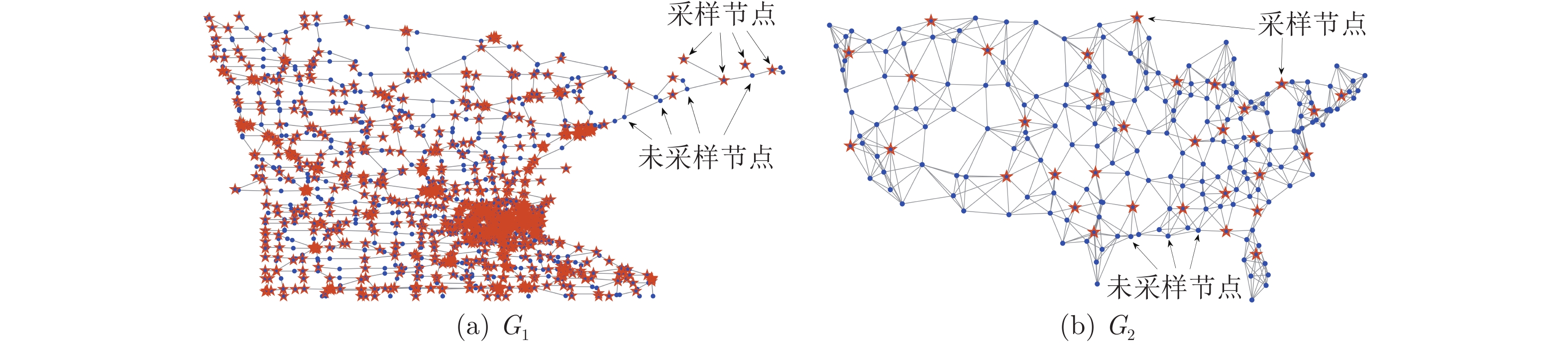
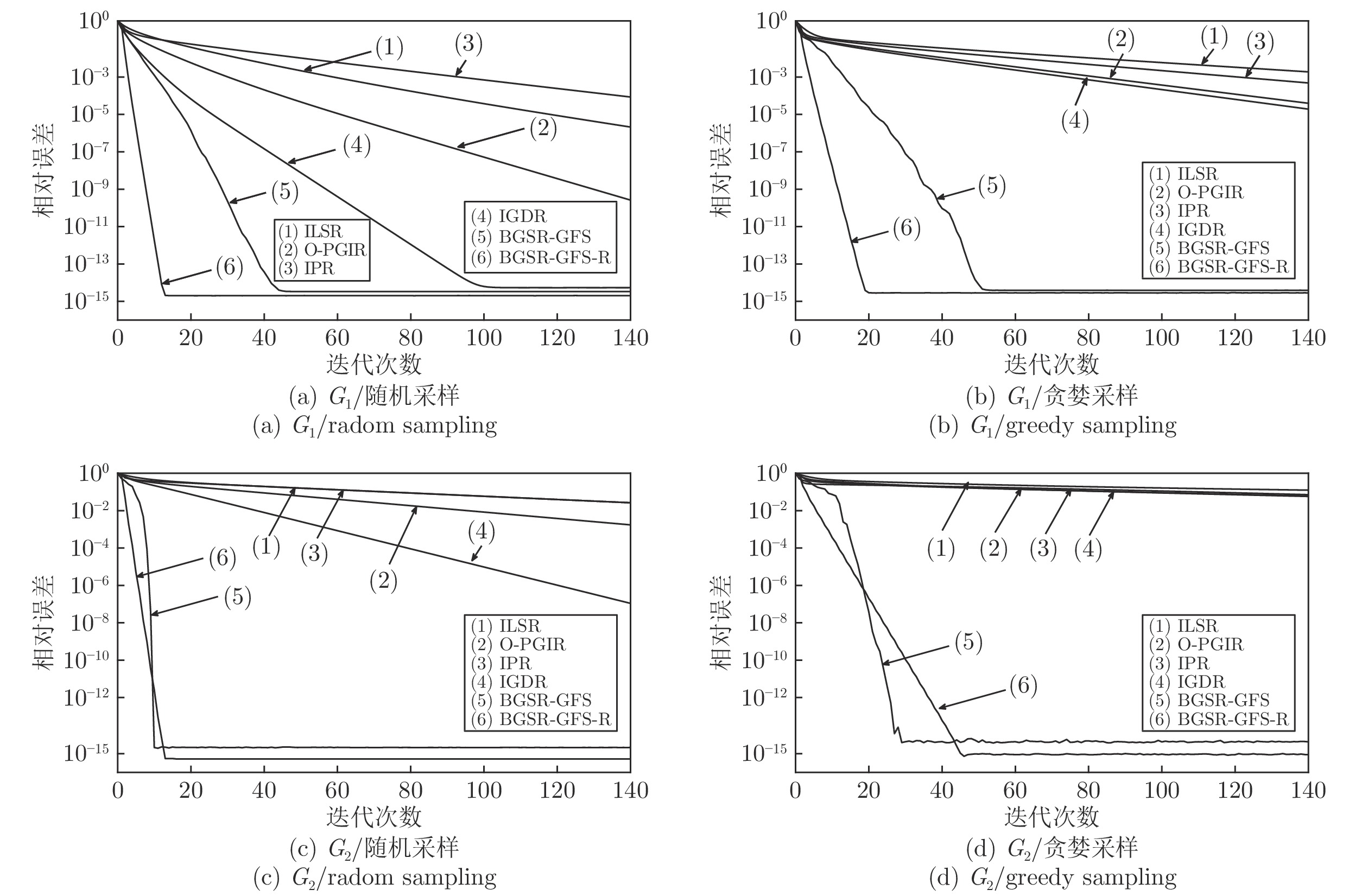
表 1 无噪情况下基于随机采样的
${G_1}$ 重构效率Table 1
${G_1}$ reconstruction efficiency of random sampling in noiseless算法 迭代次数 运行时间 (s) ILSR 220 139.99 OPGIR 114 108.78 IPR 96 61.87 IGDR 33 20.47 BGSR-GFS 27 5.73 BGSR-GFS-R 8 8.97 表 2 无噪情况下基于随机采样的
${G_2}$ 重构效率Table 2
${G_2}$ reconstruction efficiency of random sampling in noiseless算法 迭代次数 运行时间 (s) ILSR 269 0.1509 OPGIR 139 0.1291 IPR 64 0.0405 IGDR 34 0.0271 BGSR-GFS 7 0.0065 BGSR-GFS-R 5 0.0146 -
[1] 刘建伟, 黎海恩, 罗雄麟. 概率图模型学习技术研究进展[J]. 自动化学报, 2014, 40(06): 1025-1044.Liu Jian-Wei, Li Hai-En, Luo Xiong-Lin. Learning technique of probabilistic graphical models: a review. Acta Automatica Sinica, 2014, 40(6): 1025−1044. [2] Shuman D I, Narang S K, Frossard P, Ortega A, Vandergheynst P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Processing Magazine, 2013, 30(3): 83-98 doi: 10.1109/MSP.2012.2235192 [3] Tremblay N, Gonalves P, Borgnat P. Design of graph filters and filterbanks. Cooperative and Graph Signal Processing. Academic Press, 2018: 299−324 [4] Chen S H, Varma R, Sandryhaila A, Kovačević J. Discrete signal processing on graphs: Sampling theory. IEEE Transactions on Signal Processing, 2015, 63(24): 6510-6523 doi: 10.1109/TSP.2015.2469645 [5] Hu W, Cheung G, Ortega A, Au O C. Multiresolution graph Fourier transform for compression of piecewise smooth images. IEEE Transactions on Image Processing, 2014, 24(1): 419-433 [6] Liu Y L, Yang L S, You K Y, Guo W B, Wang W B. Graph learning based on spatiotemporal smoothness for time-varying graph signal. IEEE Access, 2019, 7: 62372-62386 doi: 10.1109/ACCESS.2019.2916567 [7] 蒋俊正, 杨杰, 欧阳缮. 一种新的无线传感器网络中异常节点检测定位算法[J]. 电子与信息学报, 2018, 40(10): 2358-2364.Jiang Jun-Zheng, Yang Jie, Ouyang Shan. Novel method for outlier nodes detection and localization in wireless sensor networks. Journal of Electronics and Information Technology, 2018, 40(10): 2358-2364. [8] 杨杰, 蒋俊正. 利用联合图模型的传感器网络数据修复方法[J]. 西安电子科技大学学报, 2020, 47(01): 44-51.YANG Jie, JIANG Junzheng. Method for data recovery in the sensor network based on the joint graph model[J]. Journal of Xidian University, 2020, 47(1): 44-51. [9] 廖祥文, 陈兴俊, 魏晶晶, 陈国龙, 程学旗. 基于多层关系图模型的中文评价对象与评价词抽取方法[J]. 自动化学报, 2017, 43(03): 462-471.LIAO Xiang-Wen, CHEN Xing-Jun, WEI Jing-Jing, CHEN Guo-Long, CHENG Xue-Qi. A Multi-layer Relation Graph Model for Extracting Opinion Targets and Opinion Words. Acta Automatica Sinica, 2017, 43(3): 462-471. [10] 张建朋, 裴雨龙, 刘聪, 李邵梅, 陈鸿昶. 基于因子图模型的动态图半监督聚类算法[J]. 自动化学报, 2020, 46(04): 670-680.ZHANG Jian-Peng, PEI Yu-Long, LIU Cong, LI Shao-Mei, CHEN Hong-Chang. A Semi-supervised Clustering Algorithm Based on Factor Graph Model for Dynamic Graphs. Acta Automatica Sinica, 2020, 46(4): 670-680. [11] Ortega A, Frossard P, Kovačević J, Moura J M F, Vandergheyns P. Graph signal processing: Overview, challenges, and applications. Proceedings of the IEEE, 2018, 106(5): 808-828. doi: 10.1109/JPROC.2018.2820126 [12] Tanaka Y. Spectral domain sampling of graph signals[J]. IEEE Transactions on Signal Processing, 2018, 66(14): 3752-3767. doi: 10.1109/TSP.2018.2839620 [13] Guler B, Avestimehr S, Ortega A. TACC: Topology-Aware Coded Computing for Distributed Graph Processing[J]. IEEE Transactions on Signal and Information Processing over Networks, 2020, 6(99): 508-525. [14] Hosseinalipour S, Wang J, Dai H Y, Wang W Y. Detection of infections using graph signal processing in heterogeneous networks. In: Proceedings of the 2017 IEEE Global Communications Conference. Singapore, Singapore: IEEE, 2017.1−6. [15] Shuman D I, Faraji M J, Vandergheynst P. A multiscale pyramid transform for graph signals[J]. IEEE Transactions on Signal Processing, 2015, 64(8): 2119-2134. [16] Shen Y, Baingana B, Giannakis G B. Tensor decompositions for identifying directed graph topologies and tracking dynamic networks[J]. IEEE Transactions on Signal Processing, 2017, 65(14): 3675-3687. doi: 10.1109/TSP.2017.2698369 [17] Tanaka Y, Eldar Y C, Ortega A, Cheung G. Sampling signals on graphs: From theory to applications. IEEE Signal Processing Magazine, 2020, 37(6): 14-30 doi: 10.1109/MSP.2020.3016908 [18] Ferreira P. Interpolation and the Discrete Papoulis Gerchberg Algorithm[J]. IEEE Transactions on Signal Processing, 1994, 42(10): 2596-2606. doi: 10.1109/78.324726 [19] Narang S K, Gadde A, Sanou E, Ortega A. Localized iterative methods for interpolation in graph structured data. In: Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing. Austin, TX, USA: IEEE, 2013. 491−494 [20] Wang X, Liu P, Gu Y. Local-set-based graph signal reconstruction[J]. IEEE Transactions on Signal Processing, 2015, 63(9): 2432-2444. doi: 10.1109/TSP.2015.2411217 [21] Yang L S, You K Y, Guo W B. Bandlimited graph signal reconstruction by diffusion operator. EURASIP Journal on Advances in Signal Processing, 2016, Article number: 120 (2016) [22] Brugnoli E, Toscano E, Vetro C. Iterative Reconstruction of Signals on Graph[J]. IEEE Signal Processing Letters, 2019, 27: 76-80. [23] Tseng C C, Lee S L. A missing data recovery method of sparse graph signal in GFT domain. In: Proceedings of the 2018 IEEE International Conference on Consumer Electronics. Taipei, China: IEEE, 2018. 1−2 [24] Tseng C C, Lee S L, Su R H. A missing temperature data estimation method using graph Fourier transform. In: Proceedings of the 2017 IEEE International Conference on Consumer Electronics. Taipei, China: IEEE, 2017. 87−88 [25] Sandryhaila A, Moura J M F. Discrete signal processing on graphs: Graph Fourier transform. In: Proceedings of the 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing. Vancouver, BC, Canada: IEEE, 2013. 6167−6170. [26] Narang S K, Gadde A, Ortega A. Signal processing techniques for interpolation in graph structured data. In: Proceedings of the 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing. Vancouver, BC, Canada: IEEE, 2013. 5445−5449. [27] Chen S H, Varma R, Singh A, Kovačević J. Representations of piecewise smooth signals on graphs. In: Proceedings of the 2016 IEEE International Conference on Acoustics, Speech, and Signal Processing. Shanghai, China: IEEE, 2016. 6370−6374 [28] Youla D C, Webb H. Image restoration by the method of convex projections: Part I-Theory[J]. IEEE Transactions on Medical Imaging, 1982, 1(2), 81–94. doi: 10.1109/TMI.1982.4307555 [29] Narang S K, Ortega A. Perfect reconstruction two-channel wavelet filter banks for graph structured data[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2786-2799. doi: 10.1109/TSP.2012.2188718 [30] Sandryhaila A, Moura J M F. Discrete signal processing on graphs[J]. IEEE Transactions on Signal Processing, 2013, 61(7): 1644-1656. doi: 10.1109/TSP.2013.2238935 -




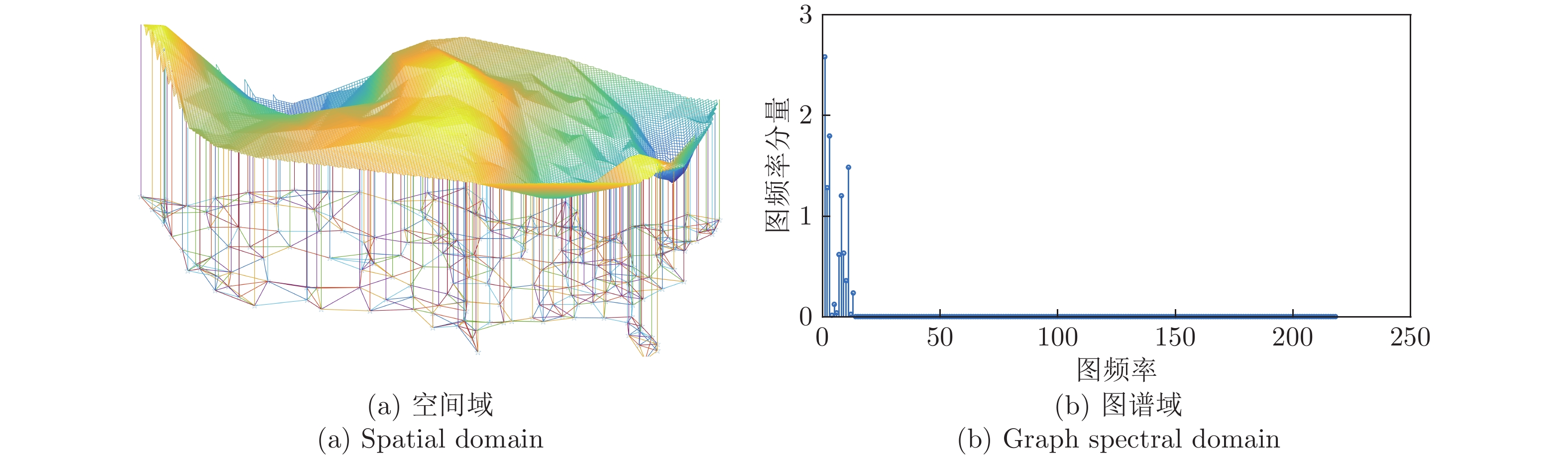
 下载:
下载: