基于改进高斯混合模型的机器人运动状态估计

葛泉波; 王贺彬; 杨秦敏; 张兴国; 刘华平

doi:10.16383/j.aas.c200660

基于改进高斯混合模型的机器人运动状态估计

doi: 10.16383/j.aas.c200660

1.
南京信息工程大学自动化学院南京 210044
2.
淳安县千岛湖科学研究院杭州 311799
3.
浙江大学控制科学与工程学院杭州 310027
4.
中国飞行试验研究院西安 710089
5.
清华大学计算机科学与技术系北京 100084

基金项目: 国家自然科学基金(61773147, 62033010)资助

详细信息

作者简介:
葛泉波：南京信息工程大学教授. 主要研究方向为工程信息融合理论与方法, 无人系统协同优化, 人机混合系统智能评估和智能电网大数据分析. 本文通信作者. E-mail: QuanboGe@163.com

王贺彬：2021年获得杭州电子科技大学硕士学位. 主要研究方向为多智能体控制和非线性非高斯状态估计. E-mail: syeaxb@163.com

杨秦敏：浙江大学控制科学与工程学院教授. 主要研究方向为工业大数据, 智慧能源系统和信息驱动的控制与优化. E-mail: qmyang@zju.edu.cn

张兴国：中国飞行试验研究院高级工程师. 主要研究方向为飞行器试飞测试技术和智能化测试技术. E-mail: cftezhang@qq.com

刘华平：清华大学计算机科学与技术系副教授. 主要研究方向为机器人感知, 学习与控制和多模态信息融合. E-mail: hpliu@tsinghua.edu.cn

计量
- 文章访问数: 1687
- HTML全文浏览量: 552
- PDF下载量: 382
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-17
- 录用日期: 2021-05-12
- 网络出版日期: 2021-11-21
- 刊出日期: 2022-06-01

Estimation of Robot Motion State Based on Improved Gaussian Mixture Model

1.
School of Automation, Nanjing University of Information Science and Technology, Nanjing 210044
2.
Qiandao Lake Institute of Science of Chun＇an, Hangzhou 311799
3.
College of Control Science and Engineering, Zhejiang University, Hangzhou 310027
4.
Chinese Flight Test Establishment, Xi＇an 710089
5.
Department of Computer Science and Technology, Tsinghua University, Beijing 100084

Funds: Supported by National Natural Science Foundation of China (61773147, 62033010)

More Information

Author Bio:
GE Quan-Bo　Professor at Nanjing University of Information Science and Technology. His research interest covers engineering information fusion theory, coordinated optimization for autonomous systems, intelligent evaluation for human-machine hybrid system, and big data in smart grid. Corresponding author of this paper

WANG He-Bin　He received his master degree from Hangzhou Dianzi University. His research interest covers multi-agent control and nonlinear non-Gaussian state estimation

YANG Qin-Min　Professor at the College of Control Science and Engineering, Zhejiang University. His research interest covers industrial big data, smart energy systems, information driven control and optimization

ZHANG Xing-Guo　Senior engineer at Chinese Flight Test Establishment. His research interest covers aircraft flight test technology and intelligent test technology

LIU Hua-Ping　Associate professor in the Department of Computer Science and Technology, Tsinghua University. His research interest covers robotic perception, learning and control, and muti-mode information fusion

摘要

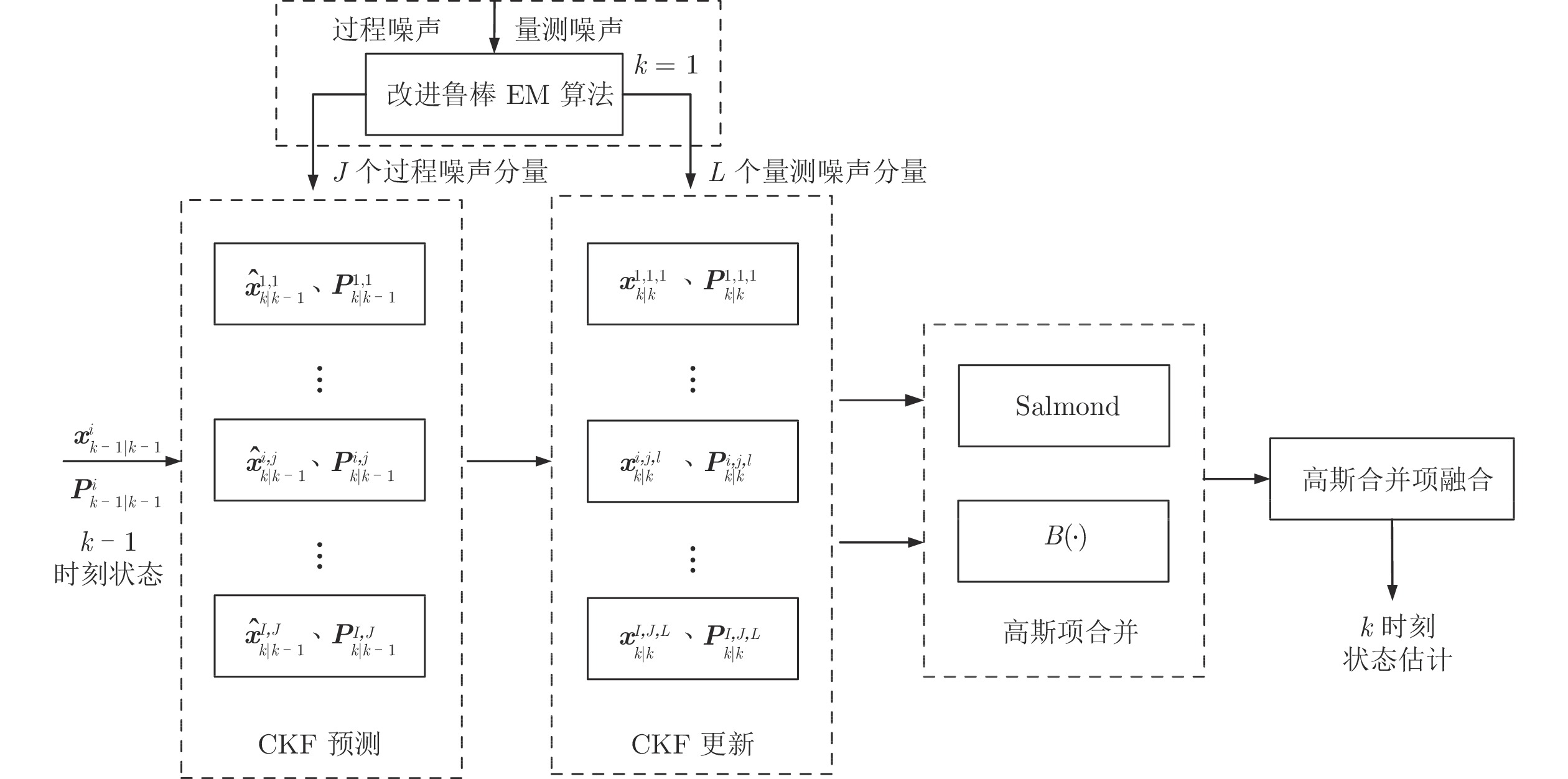
摘要: 针对复杂环境下机器人运动状态估计的精度改善问题, 提出一种面向非线性非高斯系统的改进高斯和容积卡尔曼滤波估计方法. 首先, 引入加权信息量概念来改进期望最大化算法目标函数惩罚项, 使得在优化过程中能考虑更全面的参数信息, 以达到减少期望最大化算法的迭代次数和提高收敛速度的目的. 此外, 以基于马氏距离和Kullback-Leibler (KL)距离的高斯项合并方法为基础, 提出一种能有效联合两类高斯项合并方式的融合模式. 先单独使用马氏距离和KL距离进行高斯混合项合并, 再对获得的高斯混合项进行加权融合处理, 以改善高斯和滤波中多高斯项的合并性能和保真度. 最后, 应用非线性非高斯系统的高斯和容积卡尔曼滤波框架实现对复杂环境下机器人的运动状态估计. 理论分析与仿真结果表明, 该方法能实现对机器人运动更好的状态估计精度, 并具有更强的鲁棒性能.
- 非线性非高斯系统 /
- 状态估计 /
- 高斯和容积卡尔曼滤波 /
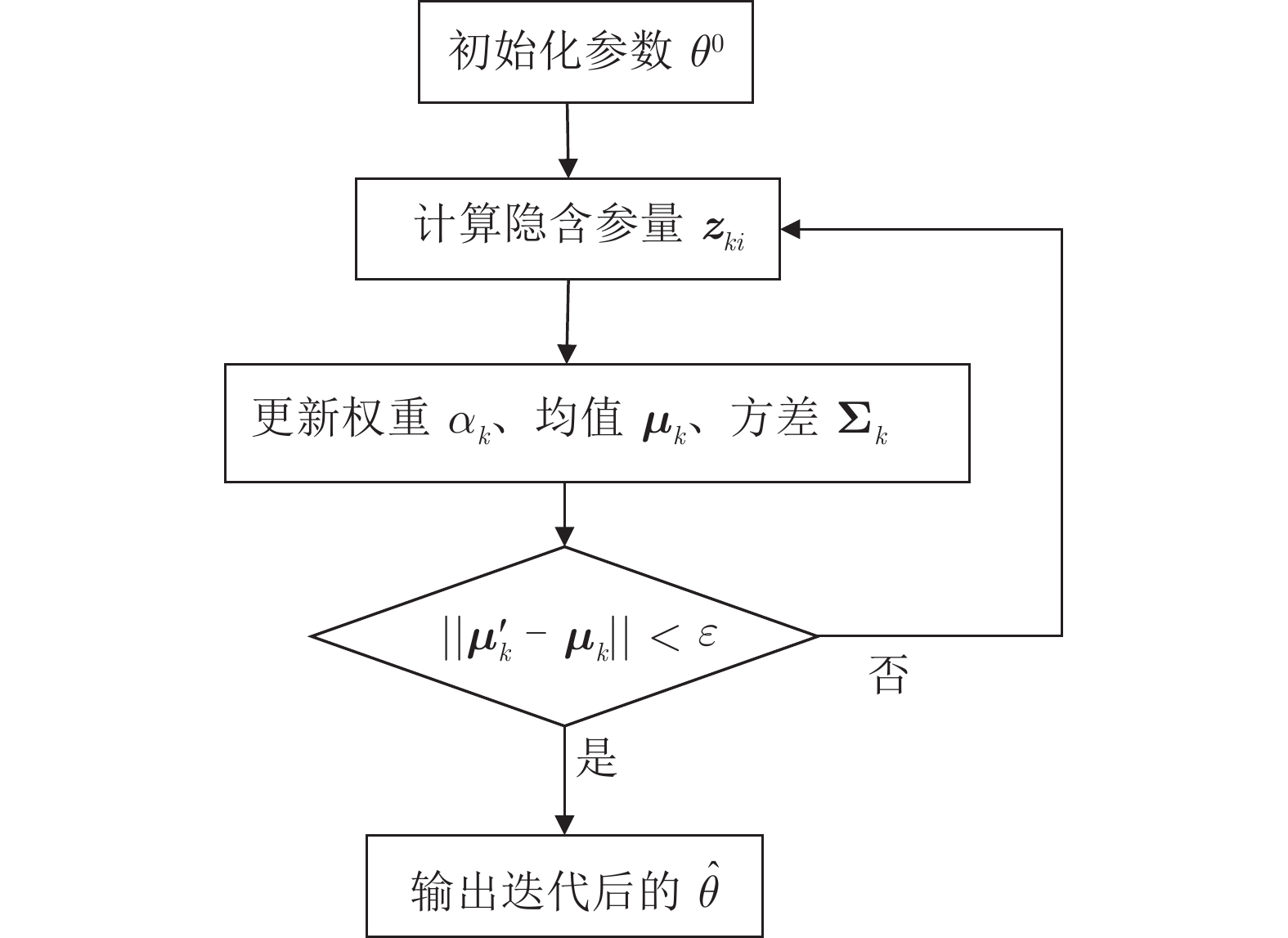
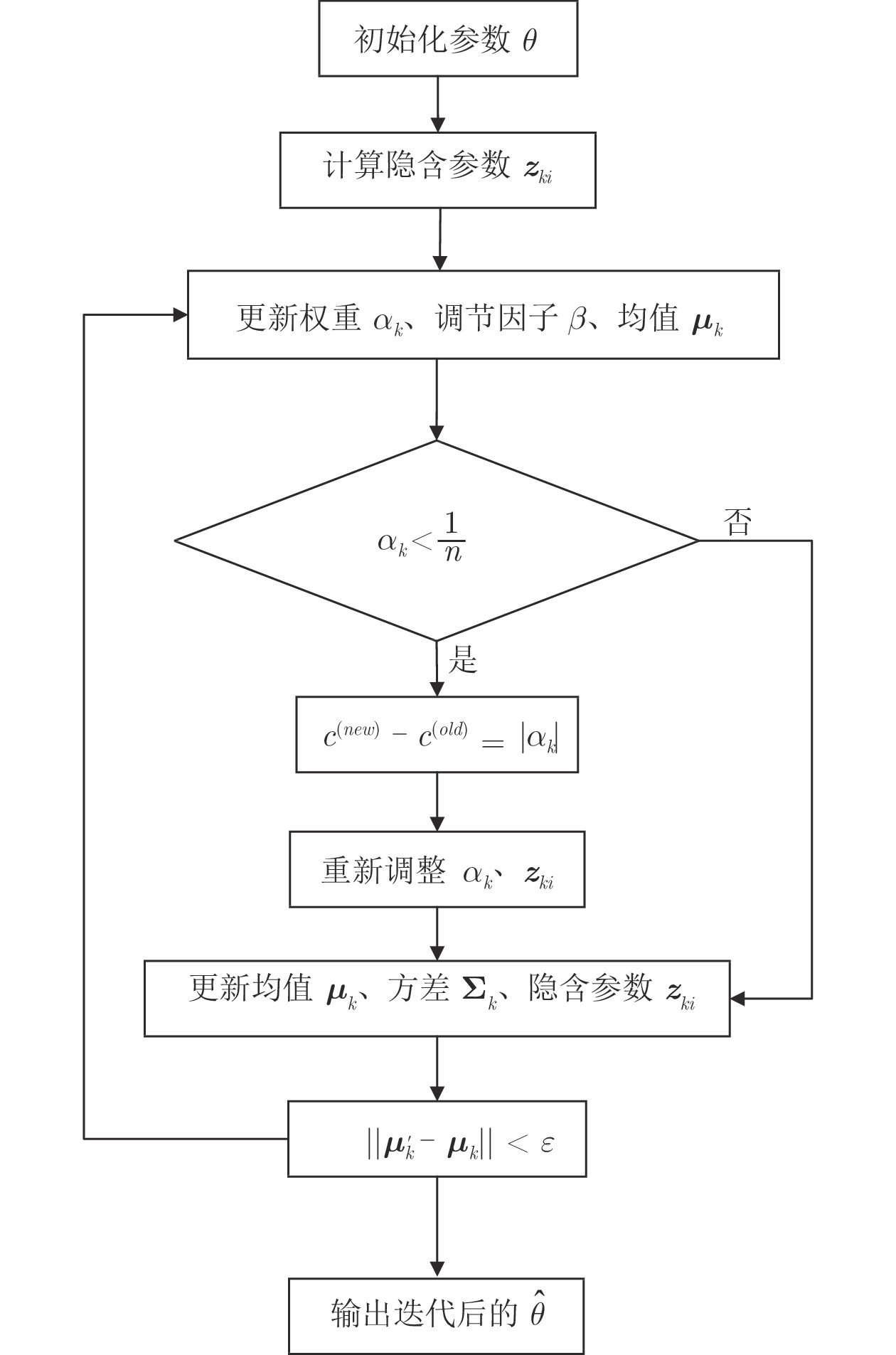
- 鲁棒期望最大化算法 /
- 凸组合融合
Abstract: For robot motion state estimation accuracy under complex environment to improve the problem, an improved Gaussian summation cubature Kalman filter is proposed for a kind of nonlinear non-Gaussian system by improving expectation-maximum algorithm and Gauassian merging method. Firstly, the weighted information is introduced to help improve the penalty item of the objective function in the expectation-maximum algorithm, so that more comprehensive parameter information can be considered in the optimization process to achieve the purpose of reducing the number of iterations of the EM algorithm and increasing the convergence speed. Then, based on the Gaussian merging methods using the Mahalanobis distance and the Kullback-Leibler distance, respectively, one fusion mode that can effectively combine the two types of Gaussian merging method is proposed. The Mahalanobis distance and the Kullback-Leibler distance are used to merge the Gaussian mixture items separately, and then the obtained Gaussian mixture items are weighted and fused to improve the merging performance and fidelity of multiple Gaussian items in the Gaussian sum filtering. Finally, the Gaussian sum cubature Kalman filter framework of nonlinear non-Gaussian system is applied to estimate the motion state of the robot in complex environment. Theoretical analysis and simulation results show that the new method can achieve better state estimation accuracy for robot motion and obtain stronger robust performance.
- Nonlinear non-Gaussian system /
- state estimation /
- Gaussian-sum cubature Kalman filter /
- robust expectation-maximum algorithm /
- convex combination fusion

HTML全文

图 1 高斯和容积卡尔曼滤波算法流程

Fig. 1 GSCKF algorithm process

下载: 全尺寸图片幻灯片

图 2 EM算法迭代流程

Fig. 2 EM algorithm process

下载: 全尺寸图片幻灯片

图 3 改进鲁棒EM算法迭代流程

Fig. 3 Improved robust EM algorithm process

下载: 全尺寸图片幻灯片

图 4 改进高斯和容积卡尔曼滤波

Fig. 4 Improved Gaussian-sum cubature Kalman filter

下载: 全尺寸图片幻灯片

图 5 改进鲁棒EM算法迭代过程

Fig. 5 Improved robust EM algorithm iterative process

下载: 全尺寸图片幻灯片

图 6 鲁棒EM算法迭代过程

Fig. 6 Robust EM algorithm iterative process

下载: 全尺寸图片幻灯片

图 7 3种算法对于机器人状态估计

Fig. 7 Three algorithms for robot state estimation

下载: 全尺寸图片幻灯片

图 8 3种算法的RMSE

Fig. 8 RMSE of three algorithms

下载: 全尺寸图片幻灯片

图 9 3种算法的方位角误差

Fig. 9 The azimuth error of three algorithms

下载: 全尺寸图片幻灯片

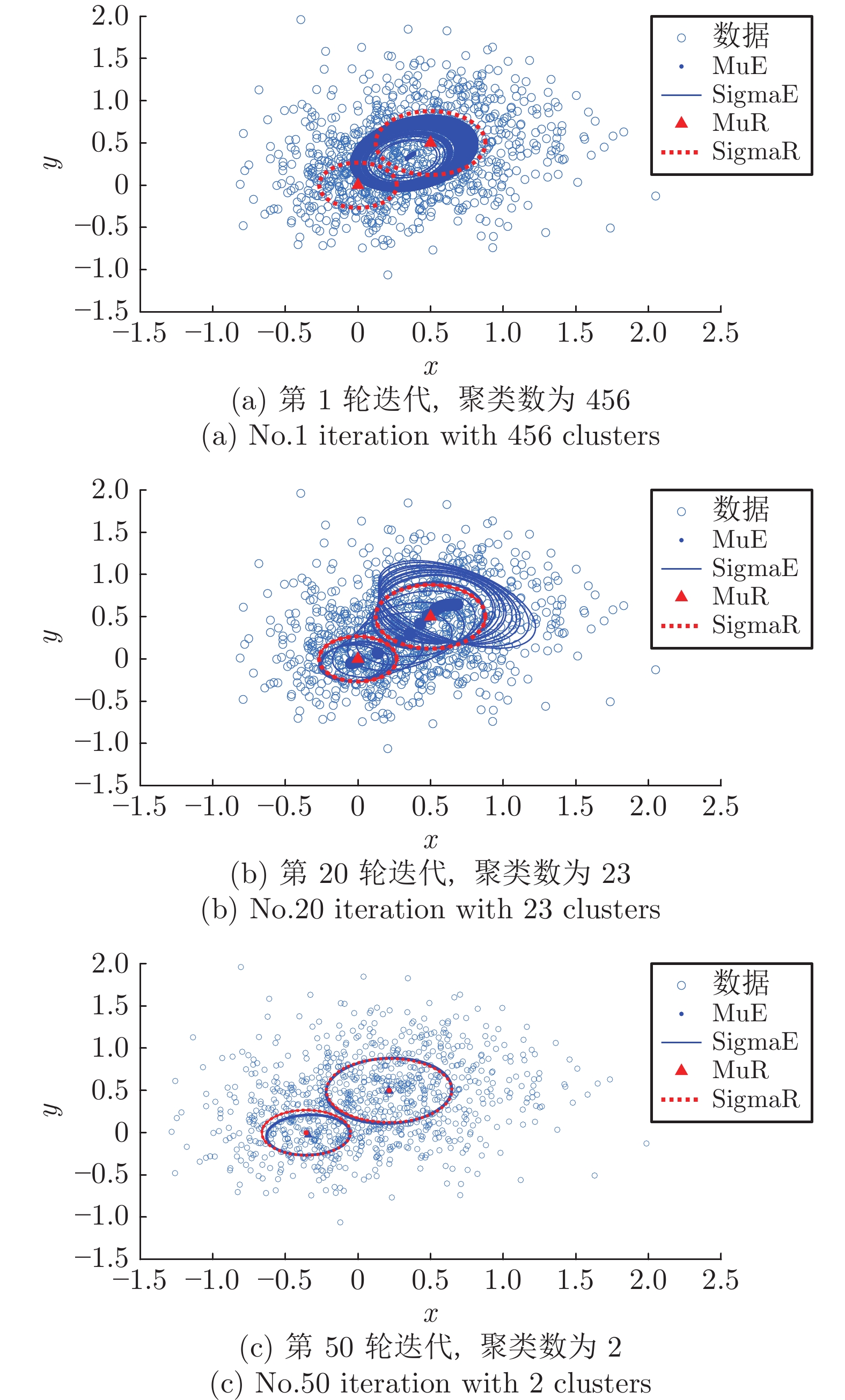
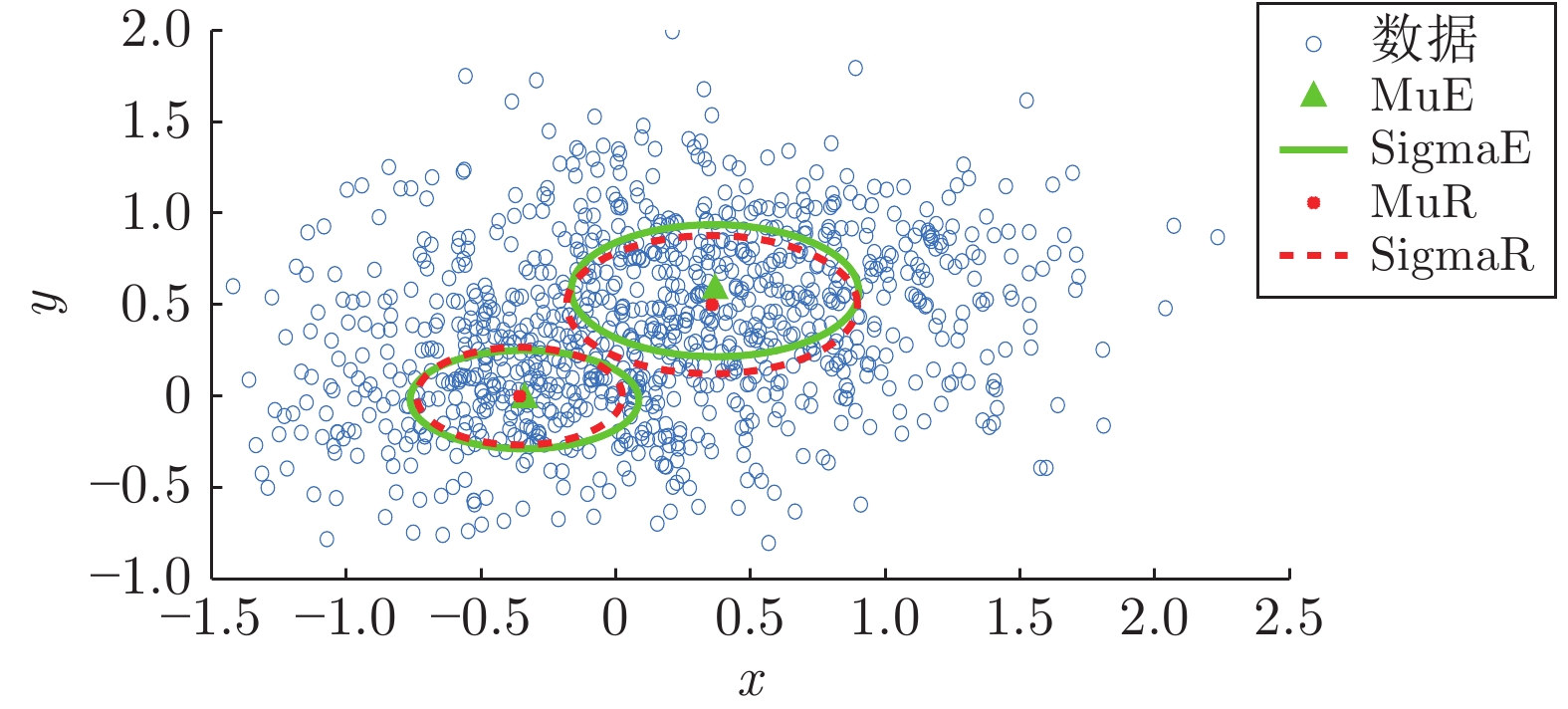
表 1 改进前后鲁棒EM算法对比

Table 1 Comparison of robust EM algorithms before and after improvement

算法迭代次数 (次) 马氏距离

文献 [21] 算法 143 0.0073
本文改进算法 50 0.0012

下载: 导出CSV

表 2 3种算法RMSE及运行时间

Table 2 RMSE and running time of 3 algorithms

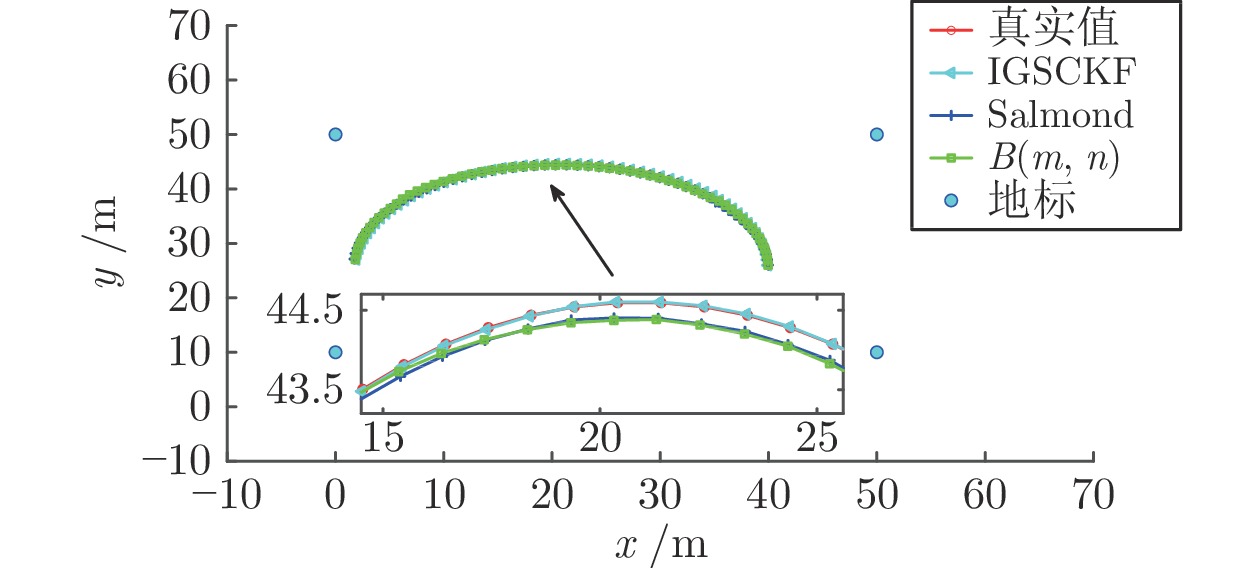
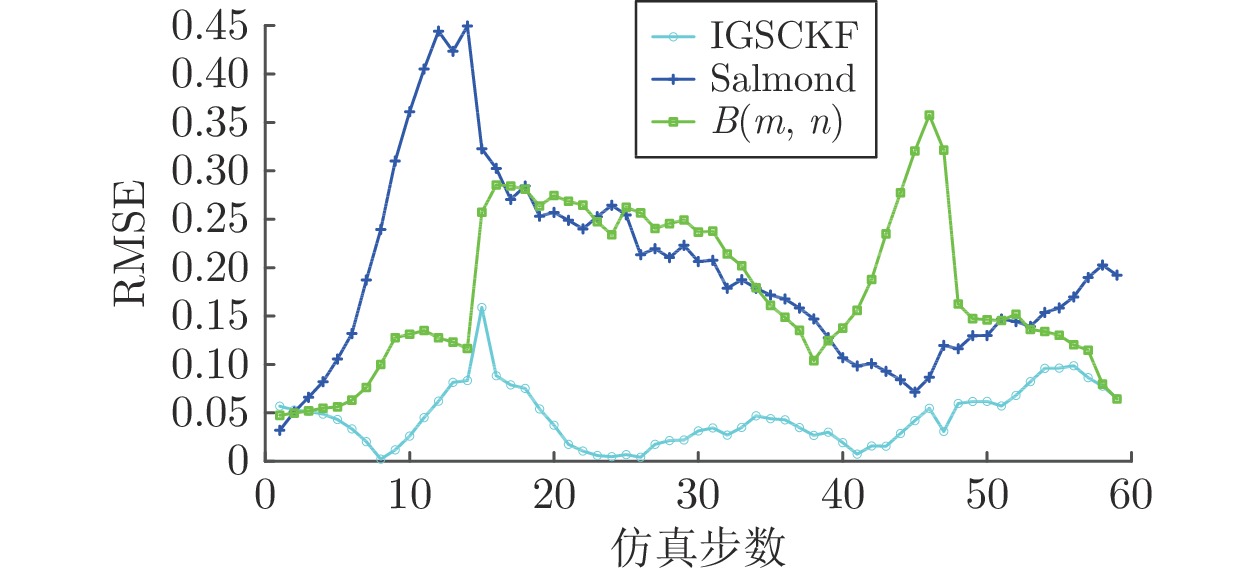
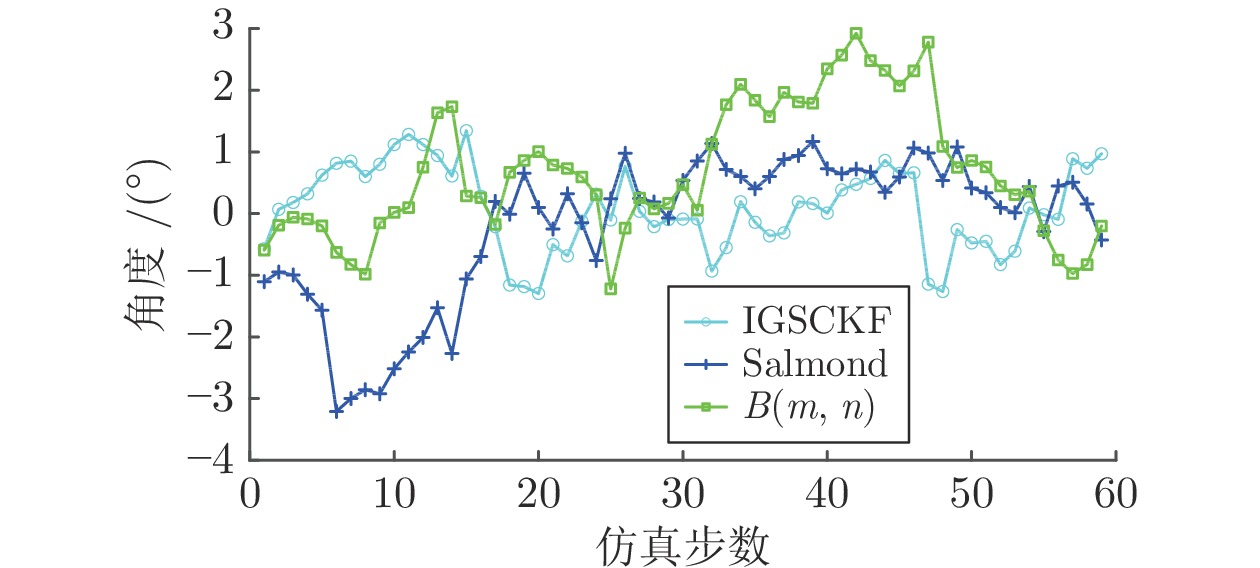
算法 RMSE (m) 运行时间 (s)

Salmond 0.0705 1.16
$B( \cdot ) $ 0.17 1.06
IGSCKF 0.0576 1.20

下载: 导出CSV

参考文献(24)

[1]	Leong P H, Arulampalam S, Lamahewa T A, et al. A Gaussian-Sum Based Cubature Kalman Filter for Bearings-Only Tracking. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1161-1176. doi: 10.1109/TAES.2013.6494405
[2]	Li W, Jia Y. Distributed Consensus Filtering for Discrete-Time Nonlinear Systems with Non-Gaussian Noise. Signal Processing, 2012, 92(10): 2464-2470. doi: 10.1016/j.sigpro.2012.03.009
[3]	王磊, 程向红, 李双喜. 高斯和高阶无迹卡尔曼滤波算法. 电子学报, 2017, 45(2): 424-430 doi: 10.3969/j.issn.0372-2112.2017.02.022 Wang Lei, Cheng Xiang-hong, Li Shuang-xi. Gaussian Sum High Order Unscented Kalman Filtering Algorithm. Acta Electronica Sinica, 2017, 45(2): 424-430 doi: 10.3969/j.issn.0372-2112.2017.02.022
[4]	江涛, 钱富才, 杨恒占, 胡绍林. 具有双重不确定性系统的联合滤波算法. 自动化学报, 2016, 42(4): 535-544 Jiang Tao, Qian Fu-cai, Yang Heng-zhan, Hu Shao-lin. A New Combined Filtering Algorithm for Systems with Dual Uncertainties. Acta Automatica Sinica, 2016, 42(4): 535-544
[5]	宋宇, 孙富春, 李庆玲. 移动机器人的改进无迹粒子滤波蒙特卡罗定位算法. 自动化学报, 2010, 36(6): 851-857 doi: 10.3724/SP.J.1004.2010.00851 Song Yu, Sun Fu-chun, Li Qing-ling. Mobile Robot Monte Carlo Localization Based on Improved Unscented Particle Filter. Acta Automatica Sinica, 2010, 36(6): 851-857 doi: 10.3724/SP.J.1004.2010.00851
[6]	Ge Q, Shao T, Yang Q, et al. Multisensor Nonlinear Fusion Methods Based on Adaptive Ensemble Fifth-Degree Iterated Cubature Information Filter for Biomechatronics. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(7), 912-925. doi: 10.1109/TSMC.2016.2523911
[7]	Ienkaran Arasaratnam, Simon Haykin. Cubature Kalman Filters. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. doi: 10.1109/TAC.2009.2019800
[8]	葛泉波, 李宏, 文成林. 面向工程应用的Kalman滤波理论深度分析. 指挥与控制学报, 2019, 5(3): 167-180 Ge Quan-bo, Li Hong, Wen Cheng-lin. Deep Analysis of Kalman Filtering Theory for Engineering Applications. Journal of Command and Control, 2019, 5(3): 167-180
[9]	Izanloo R, Fakoorian S A, Yazdi H S, Simon D. Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise. In Proceedings of the 2016 Annual Conference on Information Science and Systems, Princeton, USA: 2016. 500−505
[10]	Badong Chen, Liu X, Zhao H, et al. Maximum correntropy Kalman filter. Automatica, 2017, 76: 70-77. doi: 10.1016/j.automatica.2016.10.004
[11]	Alspach D, Sorenson H. Nonlinear Bayesian estimation using Gaussian sum approximations. IEEE Transactions on Automatic Control, 1972, 17(4): 439-448. doi: 10.1109/TAC.1972.1100034
[12]	许红, 谢文冲, 王永良. 角闪烁噪声下的高斯和容积卡尔曼滤波算法. 系统工程与电子技术, 2019, 41(02): 6-12 Xu Hong, Xie Wen-chong, Wang Yong-liang. Gaussian sum cubature Kalman tracking filter with angle glint noise. Systems Engineering and Electronics, 2019, 41(02): 6-12
[13]	Lei M, Han C Z. Expectation-maximization (EM) algorithm based on IMM filtering, with adaptive noise covariance. Acta Automatica Sinica, 2006, 32(1): 28−37
[14]	张帆, 施化吉, 周从华, 李雷. 基于高斯和的二阶扩展卡尔曼滤波算法. 信息技术, 2017(12): 84-89 Zhang Fan, Shi Hua-ji, Zhou Cong-hua, Li Lei. Two-order extended Kalman filter algorithm based on Gaussian sum. Information Technology, 2017(12): 84-89
[15]	Dempster A P, Laird N M, Rubin D B.Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 1977, 39(1): 1-38. doi: 10.1111/j.2517-6161.1977.tb01600.x
[16]	Chamroukhi F. Robust EM algorithm for model-based curve clustering. In: Proceedings of the International Joint Conference on Neural Networks (IJCNN), Dallas, USA: 2013. 1−8
[17]	邢长征, 赵全颖, 王星, 王伟. 基于鲁棒高斯混合模型的加速EM算法研究. 计算机应用研究, 2017, 34(4): 1042-1046 doi: 10.3969/j.issn.1001-3695.2017.04.019 Xing Chang-zheng, Zhao Quan-ying, Wang Xing, Wang Wei. Accelerated EM algorithm research based on robust Gaussian mixture model. Application Research of Computers, 2017, 34(4): 1042-1046 doi: 10.3969/j.issn.1001-3695.2017.04.019
[18]	Salmond D J. Mixture reduction algorithms for target tracking in clutter. In: Proceedings of the SPIE−The International Society for Optical Engineering, Orlando, USA: 1990. 434−445
[19]	Runnalls, A. R. Kullback-Leibler Approach to Gaussian Mixture Reduction. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 989-999. doi: 10.1109/TAES.2007.4383588
[20]	侯威翰, 郭莹. 非高斯噪声环境下的稀疏自适应滤波算法研究. 通信技术, 2019, 52(01): 17-23 HouWei-Han, Guo Ying. Research on sparse adaptive filtering algorithm in non-Gaussian noise environment. Communications Technology, 2019, 52(1): 11-17
[21]	Yang M S, Lai C Y, Lin C Y. A robust EM clustering algorithm for Gaussian mixture models. Pattern Recognition, 2012, 45(11): 3950-3961. doi: 10.1016/j.patcog.2012.04.031
[22]	Zhu H, Chen S, Han C. Fusion of Gaussian mixture models for possible mismatches of sensor model. Information Fusion, 2014, 20: 203-212. doi: 10.1016/j.inffus.2014.02.002
[23]	卢玉桂. EM算法在多层线性模型参数估计中的应用. 南宁: 广西大学出版社, 2013. Lu Yu-Gui. Application of EM Algorithm to Parameter Estimation of Hierarchical Linear Models. Nanning: Guangxi University Press, 2013.
[24]	王硕, 宋申民, 史小平, 于浛. 噪声特性未知的多传感器协方差交叉融合姿态估计. 控制与决策, 2016, 000(002): 273-278 Wang Shuo, Song Shen-min, Shi Xiao-ping, Yu Han. Multi-sensor covariance intersection fusion attitude estimation with unknown noise characteristics. Control and Decision, 2016, 000(002): 273-278