-
摘要: 提出一套针对加权Möller算法的广义加权规则用于探讨改进并行提取次成分分析的理论和方法问题.该规则仅在加权Möller算法上引入一个加权规则参数, 通过调节参数后算法性能上的变化, 实现加权Möller算法稳定性在动力学层面上的分析, 探讨加权参数变化对算法稳定性的影响.基于常微分方程方法对所提出规则下的加权Möller算法进行稳定性证明, 并分析其中关键函数的性质.最后, MATLAB仿真验证了所提出规则的性能和算法性质.Abstract: A generalized weighted rule for weighted Möller algorithm is introduced to explore the modified minor component analysis by parallel extraction in theory and application. The proposed rule helps to analyze the stability in the dynamic of the algorithm in aspects of different properties, through altering the generalized weighted parameter, which is the only alterable parameter adopted in the weighted Möller algorithm. The stability analysis of the weighted Möller algorithm modified by the proposed generalized weighted rule is evaluated based on ordinary differential equation. And the analysis of the key functions is given. Finally, the properties of the modified algorithms and the ability of the proposed rule are verified by simulations in MATLAB.
-
Key words:
- Multiple minor components /
- generalized weighted rule /
- parallel extraction /
- Möller algorithm
1) 本文责任编委 谭营 -
图 2 $\delta w$的变化, $p=1$处用深色标示
Fig. 2 Change of $\delta w$ where $p=1$ is marked in deep color
图 3 方向余弦曲线(上为$p=0.6$, 下为$p=1.5$)
Fig. 3 Curves of the direction cosine ($p=0.6$ is on the top and $p=1.5$ is at the bottom)
图 4 估计模值曲线(上为$p=0.6$, 下为$p=1.5$)
Fig. 4 Curves of the estimated norm ($p=0.6$ is on the top and $p=1.5$ is at the bottom)
图 5 特征值变化(上为$p=0.6$, 下为$p=1.5$)
Fig. 5 Curves of the eigenvalues ($p=0.6$ is on the top and $p=1.5$ is at the bottom)
图 6 正交性变化(上为$p=0.6$, 下为$p=1.5$)
Fig. 6 Curves of the orthogonality ($p=0.6$ is on the top and $p=1.5$ is at the bottom)
图 7 $\delta w$值变化(上为$p=0.6$, 下为$p=1.5$)
Fig. 7 Curves of $\delta w$ ($p=0.6$ is on the top and $p=1.5$ is at the bottom)
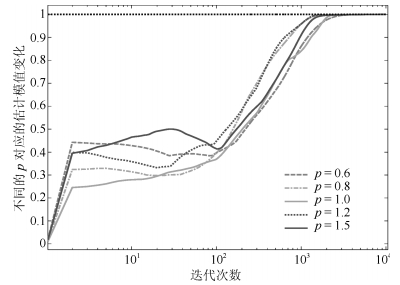
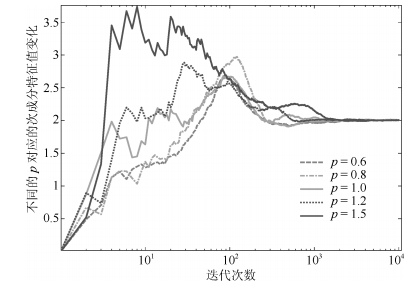
表 1 不同的$p$对应的重构误差值
Table 1 Reconstruction error rates for different $p$
$p$ 0.6 0.8 1.0 1.2 1.5 重构误差值(%) 16.383 20.126 22.878 29.369 31.047 
下载: 导出CSV
-
[1] Gao K, Ahmad M O, Swamy M. Learning algorithm for total least-squares adaptive signal processing. Electronics Letters. 1992, 28(4): 430-432. doi: 10.1049/el:19920270 [2] Feng D Z, Zheng W X, Jia Y. Neural network learning algorithms for tracking minor subspace in high-dimensional data stream. IEEE Transaction on Neural Networks, 2005, 16(3): 513-521 doi: 10.1109/TNN.2005.844854 [3] 潘宗序, 禹晶, 肖创柏, 孙卫东.基于光谱相似性的高光谱图像超分辨率算法.自动化学报, 2014, 40(12): 2797-2807 doi: 10.3724/SP.J.1004.2014.02797Pan Zong-Xu, Yu Jing, Xiao Chuang-Bai, Sun Wei-Dong. Spectral similarity-based super resolution for hyperspectral images. Acta Automatica Sinica, 2014, 40(12): 2797-2807 doi: 10.3724/SP.J.1004.2014.02797 [4] Mathew G, Reddy VU, Development and analysis of a neural network approach to pisarenko's harmonic retrieval method. IEEE Transaction on Signal Processing, 1994, 42(3): 663-667 doi: 10.1109/78.277859 [5] 程宁, 刘文举.基于多统计模型和人耳听觉特性麦克风阵列后滤波语音增强算法.自动化学报, 2010, 36(1): 74-86 doi: 10.3724/SP.J.1004.2010.00074Cheng Ning, Lie Wen-Ju. Microphone array post-filter based on multi-statistical models and perceptual properties of human ears. Acta Automatica Sinica, 2010, 36(1): 74-86 doi: 10.3724/SP.J.1004.2010.00074 [6] 齐美彬, 岳周龙, 疏坤, 蒋建国.基于广义关联聚类的分层关联多目标跟踪.自动化学报, 2017, 43(1): 152-160 doi: 10.16383/j.aas.2017.c150519Qi Mei-Bin, Yue Zhou-Long, Shu Kun, Jiang Jian-Guo. Multi-object tracking using hierarchical data association based on generalized correlation clustering graphs. Acta Automatica Sinica, 2017, 43(1): 152-160 doi: 10.16383/j.aas.2017.c150519 [7] Lei Xu, Erkki Oja, Ching Y Suen. Modified Hebbian learning for curve and surface fitting. Neural Networks, 1992, 5(3): 441-457 doi: 10.1016/0893-6080(92)90006-5 [8] Cirrincione Giansalvo, Cirrincione Maurizio, Hérault Jeanny, Van Huffel Sabine, The MCA EXIN neuron for the minor component analysis. IEEE Transaction on Neural Networks, 2002, 13(1): 160-187 doi: 10.1109/72.977295 [9] Ralf Möller. A self-stabilizing learning rule for minorcomponent analysis. International Journal of Neural Systems, 2004, 14(1): 1-8 doi: 10.1142/S0129065704001863 [10] Kong Xiang-Yu, Hu Chang-Hua, Han Chong-Zhao. A self-stabilizing MSA algorithm in high-dimension data stream. Neural Networks, 2010, 23(7): 865-871 doi: 10.1016/j.neunet.2010.04.001 [11] Kong X Y, Hu C H, Ma H G, Han C Z, A unified self-stabilizing neural network algorithm for principal and minor components extraction. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 185-198 doi: 10.1109/TNNLS.2011.2178564 [12] Chen T P, Shun I A, Murata N, Sequential extraction of minor components. Neural Processing Letters, 2001, 13: 195-201 doi: 10.1023/A:1011388608203 [13] Tan K K, Lv J H, Zhang Y, Huang S. Adaptive multiple minor directions extraction in parallel using a PCA neural network. Theoretical Computer Science, 2010, 411: 4200-4215 doi: 10.1016/j.tcs.2010.07.021 [14] Thameri M, Abed-Meraim, K, Belouchrani A. Low complexity adaptive algorithms for principal and minor component analysis. Digital Signal Processing, 2013, 23: 19-29 doi: 10.1016/j.dsp.2012.09.007 [15] Gao Y B, Kong X Y, Zhang H H, Hou L A, A weighted information criterion for multiple minor components and its adaptive extraction algorithms. Neural Networks, 2017, 89: 1-10 doi: 10.1016/j.neunet.2017.02.006 [16] 高迎彬, 孔祥玉, 胡昌华, 侯立安, 并行提取多个次成分的改进型Möller算法.控制与决策, 2017, 32(3): 493-497 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201703015Gao Ying-Bin, Kong Xiang-Yu, Hu Chang-Hua, Hou Li-An. Modified Möller algorithm for multiple minor components extraction. Control & Decision, 2017, 32(3): 493-497 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201703015 [17] 孔令智, 高迎彬, 李红增, 张华鹏.一种快速的多个主成分并行提取算法.自动化学报, 2017, 43(5): 835-842 doi: 10.16383/j.aas.2017.c160299Kong Ling-Zhi, Gao Ying-Bin, Li Hong-Zeng, Zhang Hua-Peng. A fast algorithm that extracts multiple principal components in parallel. Acta Automatica Sinica, 2017, 43(5): 835-842 doi: 10.16383/j.aas.2017.c160299 [18] Toshihisa T. Generalized weighted rules for principal components tracking. IEEE Transactions on Signal Processing, 2005, 53(4): 1243-1253 doi: 10.1109/TSP.2005.843698 -
计量
- 文章访问数: 1810
- HTML全文浏览量: 421
- PDF下载量: 122
- 被引次数: 0
