A Gaussian Estimation of Distribution Algorithm Using General Second-order Mixed Moment
-
摘要: 针对传统高斯分布估计算法(Gaussian estimation of distribution algorithms,GEDAs)中变量方差减小速度快、概率密度椭球体(Probability density ellipsoid,PDE)的长轴与目标函数的改进方向相垂直,从而导致算法搜索效率低、容易早熟收敛这一问题,提出一种基于一般二阶混合矩的高斯分布估计算法.该算法利用加权的优秀样本预估高斯均值,并根据沿目标函数的改进方向偏移后的均值来估计协方差矩阵.理论和数值分析表明,这一简单操作可以在不增大算法计算量的前提下自适应地调整概率密度椭球体的位置、大小和长轴方向,提高算法的搜索效率.在14个标准函数上对所提算法进行了测试,由统计出的Cohen's d效应量指标可知该算法的全局寻优能力强于传统高斯分布估计算法;与当前先进的粒子群算法、差分进化算法相比,所提算法可以在相同的函数评价次数内获得9个函数的显著优解.Abstract: Traditional Gaussian estimation of distribution algorithms (GEDAs) are confronted with issues that variable variances decrease fast and the long axis of the probability density ellipsoid (PDE) tends to be perpendicular to the improvement direction of the objective function, leading to reduction of search efficiency of GEDA and premature convergence. To alleviate these issues, this paper proposes a novel GEDA based on the general second-order mixed moment. In each iteration, this algorithm first estimates an initial mean using weighted excellent samples, then shifts the mean along the improvement direction of the objective function and estimates the covariance matrix with the new mean as the center. Theoretical and numerical analysis results both show that this simple operation can adaptively adjust the location, size and long axis direction of PDE without increasing computation. As a consequence, the search efficiency of the algorithm is improved. Experiments are conducted on 14 benchmark functions. The resultant Cohen's d effect size demonstrates that the proposed algorithm possesses stronger global optimization ability than traditional GEDA. And compared with some state-of-the-art particle swarm optimization and differential evolution algorithms, it can produce significantly superior solutions for 9 functions within the same function evaluation times.1) 本文责任编委 刘艳军
-
表 1 7种算法最终求得的函数误差值的均值和标准差
Table 1 The mean and standard deviation of the function error values obtained by 7 algorithms
函数 EMNA$_{g}$ AMaLGaM CMA-ES CLPSO CoBiDE MPEDE GSM-GEDA $f_{1}$ 2.21E+04$^{-}$
1.65E+031.63E-14$^{-}$
8.07E-141.58E-25$^{-}$
3.35E-260.00E+00$^{+}$
0.00E+000.00E+00$^{+}$
0.00E+000.00E+00$^{+}$
0.00E+003.98E-27
7.85E-28$f_{2}$ 1.10E+04$^{-}$
1.15E+032.06E-16$^{-}$
6.64E-161.12E-24$^{-}$
2.93E-258.40E+02$^{-}$
1.90E+021.60E-12$^{-}$
2.90E-121.01E-26$^{+}$
2.05E-261.78E-26
4.77E-27$f_{3}$ 1.97E+08$^{-}$
3.18E+073.37E-09$^{-}$
1.19E-085.54E-21$^{-}$
1.69E-211.42E+07$^{-}$
4.19E+067.26E+04$^{-}$
5.64E+041.01E+01$^{-}$
8.32E+001.12E-22
2.85E-23$f_{4}$ 7.17E+03$^{-}$
1.39E+032.17E-11$^{-}$
1.05E-109.15E+05$^{-}$
2.16E+066.99E+03$^{-}$
1.73E+031.16E-03$^{-}$
2.74E-036.61E-16$^{-}$
5.68E-161.89E-25
3.89E-26$f_{5}$ 2.81E+04$^{-}$
2.22E+032.46E+01$^{-}$
1.05E+012.77E-10$^{-}$
5.04E-113.86E+03$^{-}$
4.35E+028.03E+01$^{-}$
1.51E+027.21E-06$^{-}$
5.12E-068.90E-11
3.54E-11$f_{6}$ 1.79E+09$^{-}$
3.70E+081.05E+01$^{+}$
1.49E+004.78E-01$^{+}$
1.32E+004.16E+00$^{+}$
3.48E+004.13E-02$^{+}$
9.21E-029.65E+00$^{+}$
4.65E+001.75E+01
6.09E-01$f_{7}$ 1.08E+04$^{-}$
2.88E+021.79E-15$^{-}$
6.60E-151.82E-03$^{-}$
4.33E-034.51E-01$^{-}$
8.47E-021.77E-03$^{-}$
3.73E-032.36E-03$^{-}$
1.15E-030.00E+00
0.00E+00$f_{8}$ 2.10E+01$^{-}$
3.79E-022.09E+01$^{\approx}$
5.43E-022.03E+01$^{+}$
5.72E-012.09E+01$^{\approx}$
4.41E-022.07E+01$^{+}$
3.75E-012.09E+01$^{\approx}$
5.87E-012.09E+01
5.79E-02$f_{9}$ 5.46E+01$^{-}$
8.62E+003.66E+00$^{+}$
1.48E+004.45E+02$^{-}$
7.12E+010.00E+00$^{+}$
0.00E+000.00E+00$^{+}$
0.00E+000.00E+00$^{+}$
0.00E+007.48E+00
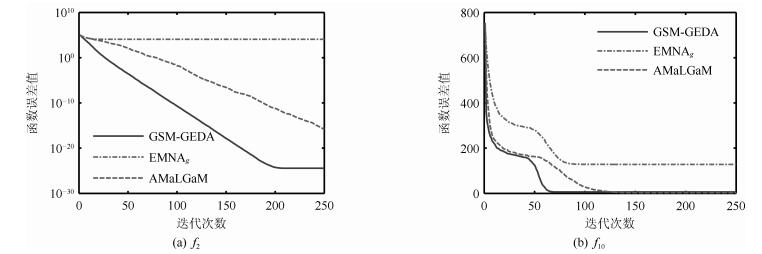
1.93E+00$f_{10}$ 1.26E+02$^{-}$
1.23E+011.91E+00$^{+}$
1.52E+004.63E+01$^{-}$
1.16E+011.04E+02$^{-}$
1.53E+014.41E+01$^{-}$
1.29E+011.52E+01$^{-}$
2.98E+006.61E+00
2.37E+00$f_{11}$ 6.25E+00$^{-}$
1.37E+003.58E-02$^{-}$
1.29E-017.11E+00$^{-}$
2.14E+002.60E+01$^{-}$
1.63E+005.62E+00$^{-}$
2.19E+002.58E+01$^{-}$
3.11E+000.00E+00
0.00E+00$f_{12}$ 4.38E+04$^{-}$
1.54E+041.06E+03$^{\approx}$
1.87E+031.26E+04$^{-}$
1.74E+041.79E+04$^{-}$
5.24E+032.94E+03$^{-}$
3.93E+031.17E+03$^{-}$
8.66E+029.45E+02
1.27E+03$f_{13}$ 3.85E+00$^{-}$
6.32E-012.85E+00$^{-}$
4.61E-013.43E+00$^{-}$
7.60E-012.06E+00$^{+}$
2.15E-012.64E+00$^{\approx}$
1.13E+002.92E+00$^{-}$
6.33E-012.77E+00
3.05E-01$f_{14}$ 1.15E+01$^{-}$
3.53E-011.13E+01$^{-}$
3.23E-011.47E+01$^{-}$
3.31E-011.28E+01$^{-}$
2.48E-011.23E+01$^{-}$
4.90E-011.23E+01$^{-}$
4.22E-011.05E+01
2.85E-01$+/{\approx}/-$
(个数)0 / 0 / 14 3 / 2/ 9 2 / 0/ 12 4 / 1 / 9 4 / 1 / 9 4 / 1 / 9 - -
[1] Larrañnaga P, Lozano J A. Estimation of Distribution Algorithms:A New Tool for Evolutionary Computation. New York, USA:Springer, 2001. 57-100 [2] Hauschild M, Pelikan M. An introduction and survey of estimation of distribution algorithms. Swarm and Evolutionary Computation, 2011, 1(3):111-128 doi: 10.1016/j.swevo.2011.08.003 [3] 王圣尧, 王凌, 方晨, 许烨.分布估计算法研究进展.控制与决策, 2012, 27(7):961-966, 974 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201207002.htmWang Sheng-Yao, Wang Ling, Fang Chen, Xu Ye. Advances in estimation of distribution algorithms. Control and Decision, 2012, 27(7):961-966, 974 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201207002.htm [4] Larrañaga P, Etxeberria R, Lozano J A, Peña J M. Optimization in continuous domains by learning and simulation of Gaussian networks. In: Proceedings of 2000 Genetic and Evolutionary Computation Conference. Las Vegas, USA: Morgan Kaufmann, 2000. 201-204 [5] Lu Q, Yao X. Clustering and learning Gaussian distribution for continuous optimization. IEEE Transactions on Systems, Man, and Cybernetics, Part C:(Applications and Reviews), 2005, 35(2):195-204 doi: 10.1109/TSMCC.2004.841914 [6] Yuan B, Gallagher M. On the importance of diversity maintenance in estimation of distribution algorithms. In: Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2005. 719-726 [7] Pošík P. Preventing premature convergence in a simple EDA via global step size setting. Parallel Problem Solving from Nature——PPSN X. Lecture Notes in Computer Science. Berlin, Heidelberg, Germany: Springer-Verlag, 2008: . 549-558 [8] Dong W S, Yao X. Unified Eigen analysis on multivariate Gaussian based estimation of distribution algorithms. Information Sciences, 2008, 178(15):3000-3023 doi: 10.1016/j.ins.2008.01.021 [9] Ocenasek J, Kern S, Hansen N, Koumoutsakos P. A mixed bayesian optimization algorithm with variance adaptation. Parallel Problem Solving from Nature——PPSN VⅢ. Lecture Notes in Computer Science., Berlin, Heidelberg, Germany: Springer-Verlag, 2004. 352-361 [10] Bosman P A N, Grahl J, Rothlauf F. SDR: a better trigger for adaptive variance scaling in normal EDAs. In: Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2007. 492-499 [11] Cai Y P, Sun X M, Xu H, Jia P F. Cross entropy and adaptive variance scaling in continuous EDA. In: Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2007. 609-616 [12] Bosman P A N, Grahl J, Thierens D. Enhancing the performance of maximum-likelihood Gaussian EDAs using anticipated mean shift. Parallel Problem Solving from Nature——PPSN X. Lecture Notes in Computer Science. Berlin, Heidelberg, Germany: Springer-Verlag, 2008: . 133-143 [13] Bosman P A N, Grahl J, Thierens D. Benchmarking parameter-free AMaLGaM on functions with and without noise. Evolutionary Computation, 2013, 21(3):445-469 doi: 10.1162/EVCO_a_00094 [14] 程玉虎, 王雪松, 郝名林.一种多样性保持的分布估计算法.电子学报, 2010, 38(3):591-597 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201003018Cheng Yu-Hu, Wang Xue-Song, Hao Ming-Lin. An estimation of distribution algorithm with diversity preservation. Acta Electronica Sinica, 2010, 38(3):591-597 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201003018 [15] Karshenas H, Santana R, Bielza C, Larrañaga P. Regularized continuous estimation of distribution algorithms. Applied Soft Computing, 2013, 13(5):2412-2432 doi: 10.1016/j.asoc.2012.11.049 [16] Yang P, Tang K, Lu X F. Improving estimation of distribution algorithm on multi-modal problems by detecting promising areas. IEEE Transactions on Cybernetics, 2015, 45(8):1438-1449 doi: 10.1109/TCYB.2014.2352411 [17] Ding N, Zhou S D, Sun Z Q. Histogram-based estimation of distribution algorithm:a competent method for continuous optimization. Journal of Computer Science and Technology, 2008, 23(1):35-43 doi: 10.1007/s11390-008-9108-0 [18] 张建华, 曾建潮.基于序贯重点采样粒子滤波的分布估计算法.电子学报, 2010, 38(12):2929-2932 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201012039Zhang Jian-Hua, Zeng Jian-Chao. Estimation of distribution algorithm based on sequential importance sampling particle filters. Acta Electronica Sinica, 2010, 38(12):2929-2932 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201012039 [19] 王丽芳, 曾建潮, 洪毅.利用Copula函数估计概率模型并采样的分布估计算法.控制与决策, 2011, 26(9):1333-1337, 1342 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzyjc201109009Wang Li-Fang, Zeng Jian-Chao, Hong Yi. Estimation of distribution algorithm modeling and sampling by means of Copula. Control and Decision, 2011, 26(9):1333-1337, 1342 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzyjc201109009 [20] Zhou A M, Sun J Y, Zhang Q F. An estimation of distribution algorithm with cheap and expensive local search. IEEE Transactions on Evolutionary Computation, 2015, 19(6):807-822 doi: 10.1109/TEVC.2014.2387433 [21] 张放, 鲁华祥.利用条件概率和Gibbs抽样技术为分布估计算法构造通用概率模型.控制理论与应用, 2013, 30(3):307-315 http://www.oalib.com/paper/4746991Zhang Fang, Lu Hua-Xiang. General stochastic model for algorithm of distribution estimation with conditional probabilities and Gibbs sampling. Control Theory & Applications, 2013, 30(3):307-315 http://www.oalib.com/paper/4746991 [22] 钟伟才, 刘静, 刘芳, 焦李成.建立在一般结构Gauss网络上的分布估计算法.电子与信息学报, 2005, 27(3):467-470 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkxxk200503032Zhong Wei-Cai, Liu Jing, Liu Fang, Jiao Li-Cheng. Estimation of distribution algorithm based on generic Gaussian networks. Journal of Electronics and Information Technology, 2005, 27(3):467-470 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkxxk200503032 [23] 赵虹. n元椭球面的判定及所围椭球体的体积.数学的实践与认识, 2013, 43(10):279-282Zhao Hong. Areas (Volumes) of n-dimension ellipsoid by quadratic curve (surface) enclosed. Mathematics in Practice and Theory, 2013, 43(10):279-282 [24] Bunch J R, Nielsen C P, Sorensen D C. Rank-one modification of the symmetric eigenproblem. Numerische Mathematik, 1978, 31(1):31-48 doi: 10.1007/BF01396012 [25] 殷庆祥.实对称矩阵的秩1修正的特征反问题.南通工学院学报(自然科学版), 2003, 2(4):11-14 http://www.doc88.com/p-9919700579946.htmlYin Qing-Xiang. The inverse problem of rank-1 modification of real symmetric matrices. Journal of Nantong Institute of Technology (Natural Science), 2003, 2(4):11-14 http://www.doc88.com/p-9919700579946.html [26] 谢平民, 陈图豪.连续型样本协差阵的正定性.中山大学学报(自然科学版), 1990, 29(1):102-104 http://www.cqvip.com/QK/94631X/199001/429070.htmlXie Ping-Min, Chen Tu-Hao. The positive definiteness of the covariance matrix of continuous sample. Acta Scientiarum Naturalium Universitatis Sunyatseni, 1990, 29(1):102-104 http://www.cqvip.com/QK/94631X/199001/429070.html [27] Suganthan P N, Hansen N, Liang J J, Deb K, Chen Y P, Auger A, Tiwari S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real Parameter Optimization, Technical Report, Nanyang Technological University, Singapore, 2005. [28] Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evolutionary Computation, 2001, 9(2):159-195 [29] Liang J J, Qin A K, Suganthan P N, Baskar S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation, 2006, 10(3):281-295 doi: 10.1109/TEVC.2005.857610 [30] Wang Y, Li H X, Huang T W, Li L. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting. Applied Soft Computing, 2014, 18:232-247 doi: 10.1016/j.asoc.2014.01.038 [31] Wu G H, Mallipeddi R, Suganthan P N, Wang R, Chen H K. Differential evolution with multi-population based ensemble of mutation strategies. Information Sciences, 2016, 329:329-345 doi: 10.1016/j.ins.2015.09.009 [32] Cohen J. Statistical Power Analysis for the Behavioral Sciences (Second Edition). Hillsdale, NJ: Lawrence Erlbaum Associates, 1988. -




 下载:
下载: