Review of Quality-related Fault Detection and Diagnosis Techniques for Complex Industrial Processes
-
摘要: 质量相关的故障检测与诊断技术是保证安全生产及获得可靠产品质量的有效手段,是当前国际过程控制领域的研究热点.首先,梳理了质量相关的故障检测技术中典型方法的基本思想和改进过程;其次,概述了质量相关的故障诊断技术中常用的贡献图法及其相关改进方法之间的联系,并通过带钢热连轧过程(Hot strip mill process,HSMP)案例比较了各种典型方法在质量相关的故障检测与诊断性能上的异同;最后,面向复杂工业过程运行数据的主要特性,评析了质量相关的故障检测与诊断方法的研究现状,并指出了该研究领域亟需解决的问题和未来的发展方向.Abstract: Quality-related fault detection and diagnosis techniques have been extensively applied to the process control field to guarantee production safety and product quality, which, thus, have recently become an active area of research both in academia and industry. Firstly, the basic idea and improvements of typical methods for quality-related fault detection techniques are introduced in this paper. Then, quality-related fault diagnosis techniques are revisited, with special case study attention on the contribution plot based methods and their improved methods, in which on a hot strip mill process (HSMP) is used to show their different performances. Finally, the state-of-the-art research of quality-related fault detection and diagnosis methods for main characteristics of complex industrial process operation data are reviewed, and open problems, challenges and perspectives for future research are presented as well.
-
Key words:
- Quality-related /
- fault detection /
- fault diagnosis /
- partial least squares (PLS) /
- contribution plot
1) 本文责任编委 胡昌华 -
表 1 对比结果
Table 1 Comparison results
方法 计算复杂度 投影结构 子空间个数 统计量个数 PLS $a$次SVDs 斜交 2 2 T-PLS $a+3$次SVDs 正交 4 4 C-PLS $a+2$次SVDs 正交 3 3 M-PLS 2次SVDs 正交 2 2 E-PLS 3次SVDs 正交 3 3 PCR 3次SVDs 正交 3 3 CVA 1次SVD 正交 2 2 表 2 监测统计量总结
Table 2 Summary of monitoring statistics
方法 质量相关故障统计量 质量无关故障统计量 PLS $T^{2}$ Q T-PLS $T_{y}^{2}$和$Q_{r}$ $T_{o}^{2}$和$T_{r}^{2}$ C-PLS $T_{c}^{2}$ $T_{x}^{2}$和$Q_{x}$ M-PLS $T_{y}^{2}$ $T_{x}^{2}$ E-PLS $T_{y}^{2}$ $T_{x}^{2}$和$Q_{x}$ PCR $T_{y}^{2}$ $T_{o}^{2}$和$Q_{o}$ CVA $T_{p}^{2}$ $T_{q}^{2}$ 表 3 过程及质量变量分配表
Table 3 Assignment table of process and quality variables
变量 类型 描述 单位 1~7 过程变量 第$i$机架的平均辊缝 ($i=1,cdots,7$) mm 8~14 过程变量 第$i$机架的轧制力 ($i=1,cdots,7$) MN 15~20 过程变量 第$i$机架的弯辊力 ($i=2,cdots,7$) MN 21 质量变量 精轧末机架出口厚度 mm 表 4 故障报警率及故障检测率对比结果
Table 4 FAR and FDR comparison results
方法 质量相关
FAR质量相关
FDR质量无关
FAR质量无关
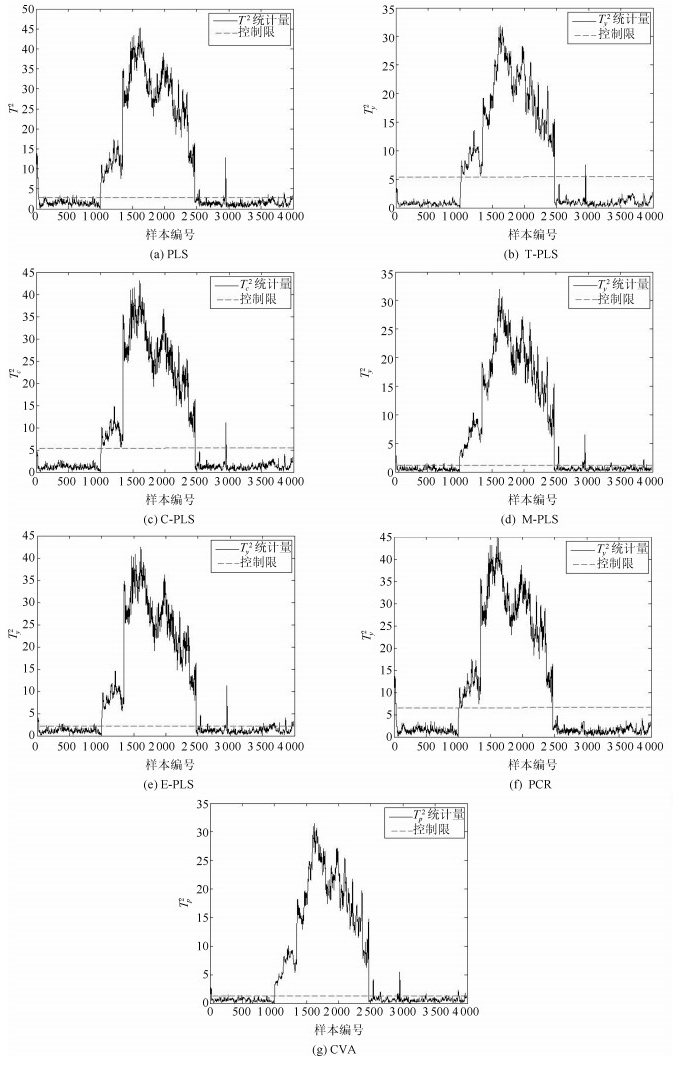
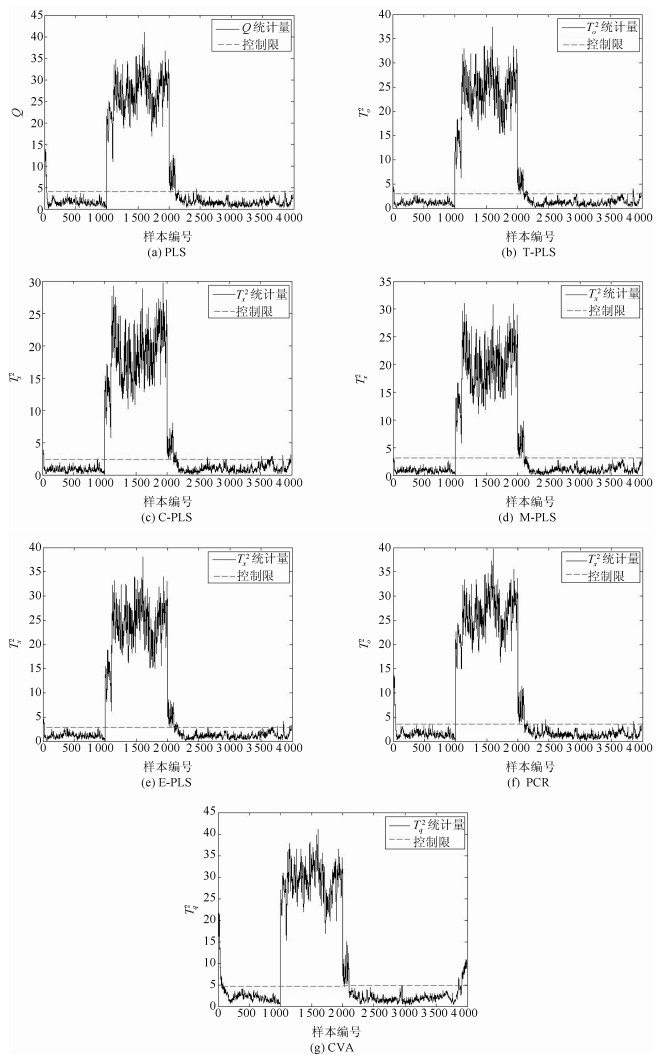
FDRPLS 0.1812 0.8680 0.0019 0.9960 T-PLS 0.2146 0.8920 0.0078 0.9981 C-PLS 0.2181 0.9713 0.0041 0.9982 M-PLS 0.1946 0.8480 0.0530 0.9981 E-PLS 0.2179 0.9712 0.0041 0.9983 PCR 0.1927 0.9014 0.0052 0.9944 CVA 0.2011 0.8966 0.0037 0.9929 -
[1] Qin S J. Survey on data-driven industrial process monitoring and diagnosis. Annual Reviews in Control, 2012, 36(2): 220-234 doi: 10.1016/j.arcontrol.2012.09.004 [2] Gao Z W, Cecati C, Ding S X. A survey of fault diagnosis and fault-tolerant techniques——Part Ⅱ: fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3768-3774 https://www.researchgate.net/publication/277641711_A_Survey_of_Fault_Diagnosis_and_Fault-Tolerant_Techniques-Part_II_Fault_Diagnosis_With_Knowledge-Based_and_HybridActive_Approaches [3] Yin S, Li X W, Gao H J, Kaynak O. Data-based techniques focused on modern industry: an overview. IEEE Transactions on Industrial Electronics, 2015, 62(1): 657-667 doi: 10.1109/TIE.2014.2308133 [4] Kano M, Nakagawa Y. Data-based process monitoring, process control, and quality improvement: recent developments and applications in steel industry. Computers & Chemical Engineering, 2008, 32(1-2): 12-24 [5] Ge Z Q, Song Z H, Gao F R. Review of recent research on data-based process monitoring. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562 https://www.researchgate.net/publication/263974651_Review_of_Recent_Research_on_Data-Based_Process_Monitoring [6] 周东华, 胡艳艳.动态系统的故障诊断技术.自动化学报, 2009, 35(6): 748-758 doi: 10.3724/SP.J.1004.2009.00748Zhou Dong-Hua, Hu Yan-Yan. Fault diagnosis techniques for dynamic systems. Acta Automatica Sinica, 2009, 35(6): 748-758 doi: 10.3724/SP.J.1004.2009.00748 [7] Qin S J, Zheng Y Y. Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures. AIChE Journal, 2013, 59(2): 496-504 doi: 10.1002/aic.v59.2 [8] Li B B, Morris A J, Martin E B. Generalized partial least squares regression based on the penalized minimum norm projection. Chemometrics and Intelligent Laboratory Systems, 2004, 72(1): 21-26 doi: 10.1016/j.chemolab.2004.01.026 [9] Ergon R. Reduced PCR/PLSR models by subspace projections. Chemometrics and Intelligent Laboratory Systems, 2006, 81(1): 68-73 doi: 10.1016/j.chemolab.2005.09.008 [10] Ding S X, Yin S, Peng K X, Hao H Y, Shen B. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2239-2247 doi: 10.1109/TII.2012.2214394 [11] Yin S, Ding S X, Haghani A, Hao H Y, Zhang P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. Journal of Process Control, 2012, 22(9): 1567-1581 doi: 10.1016/j.jprocont.2012.06.009 [12] MacGregor J F, Jaeckle C, Kiparissides C, Koutoudi M. Process monitoring and diagnosis by multiblock PLS methods. AIChE Journal, 1994, 40(5): 826-838 doi: 10.1002/(ISSN)1547-5905 [13] Wold S. Exponentially weighted moving principal components analysis and projections to latent structures. Chemometrics and Intelligent Laboratory Systems, 1994, 23(1): 149-161 doi: 10.1016/0169-7439(93)E0075-F [14] Li G, Qin S J, Zhou D H. Geometric properties of partial least squares for process monitoring. Automatica, 2010, 46(1): 204-210 doi: 10.1016/j.automatica.2009.10.030 [15] Negiz A, Çlinar A. Statistical monitoring of multivariable dynamic processes with state-space models. AIChE Journal, 1997, 43(8): 2002-2020 doi: 10.1002/(ISSN)1547-5905 [16] Russell E L, Chiang L H, Braatz R D. Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis. Chemometrics and Intelligent Laboratory Systems, 2000, 51(1): 81-93 doi: 10.1016/S0169-7439(00)00058-7 [17] Juricek B C, Seborg D E, Larimore W E. Fault detection using canonical variate analysis. Industrial & Engineering Chemistry Research, 2004, 43(2): 458-474 https://www.researchgate.net/publication/231371151_Fault_Detection_Using_Canonical_Variate_Analysis [18] Stubbs S, Zhang J, Morris J. Fault detection in dynamic processes using a simplified monitoring-specific CVA state space modelling approach. Computers & Chemical Engineering, 2012, 41: 77-87 http://eprint.ncl.ac.uk/pub_details2.aspx?pub_id=184088 [19] Chen Z W, Ding S X, Zhang K, Li Z B, Hu Z K. Canonical correlation analysis-based fault detection methods with application to alumina evaporation process. Control Engineering Practice, 2016, 46: 51-58 doi: 10.1016/j.conengprac.2015.10.006 [20] Barker M, Rayens W. Partial least squares for discrimination. Journal of Chemometrics, 2003, 17(3): 166-173 doi: 10.1002/(ISSN)1099-128X [21] De Jong S. PLS fits closer than PCR. Journal of Chemometrics, 1993, 7(6): 551-557 doi: 10.1002/(ISSN)1099-128X [22] Zhang K, Hao H Y, Chen Z W, Ding S X, Peng K X. A comparison and evaluation of key performance indicator-based multivariate statistics process monitoring approaches. Journal of Process Control, 2015, 33: 112-126 doi: 10.1016/j.jprocont.2015.06.007 [23] Peng K X, Zhang K, Dong J, You B. Quality-relevant fault detection and diagnosis for hot strip mill process with multi-specification and multi-batch measurements. Journal of the Franklin Institute, 2015, 352(3): 987-1006 doi: 10.1016/j.jfranklin.2014.12.002 [24] Pudil P, Novovičová J, Kittler J. Floating search methods in feature selection. Pattern Recognition Letters, 1994, 15(11): 1119-1125 doi: 10.1016/0167-8655(94)90127-9 [25] Abrahamsson C, Johansson J, Sparén A, Lindgren F. Comparison of different variable selection methods conducted on NIR transmission measurements on intact tablets. Chemometrics and Intelligent Laboratory Systems, 2003, 69(1-2): 3-12 doi: 10.1016/S0169-7439(03)00064-9 [26] Wold S, Antti H, Lindgren F, Öhman J. Orthogonal signal correction of near-infrared spectra. Chemometrics and Intelligent Laboratory Systems, 1998, 44(1-2): 175-185 doi: 10.1016/S0169-7439(98)00109-9 [27] Fearn T. On orthogonal signal correction. Chemometrics and Intelligent Laboratory Systems, 2000, 50(1): 47-52 doi: 10.1016/S0169-7439(99)00045-3 [28] Choi S W, Lee I B. Multiblock PLS-based localized process diagnosis. Journal of Process Control, 2005, 15(3): 295-306 doi: 10.1016/j.jprocont.2004.06.010 [29] Zhou D H, Li G, Qin S J. Total projection to latent structures for process monitoring. AIChE Journal, 2010, 56(1): 168-178 https://www.researchgate.net/publication/229883646_Total_projection_to_latent_structures_for_process_monitoring [30] Nomikos P, MacGregor J F. Multivariate SPC charts for monitoring batch processes. Technometrics, 1995, 37(1): 41-59 doi: 10.1080/00401706.1995.10485888 [31] Li G, Qin S J, Zhou D H. Output relevant fault reconstruction and fault subspace extraction in total projection to latent structures models. Industrial & Engineering Chemistry Research, 2010, 49(19): 9175-9183 https://www.researchgate.net/publication/231391323_Output_Relevant_Fault_Reconstruction_and_Fault_Subspace_Extraction_in_Total_Projection_to_Latent_Structures_Models [32] Zhao C H, Sun Y X. The multi-space generalization of total projection to latent structures (MsT-PLS) and its application to online process monitoring. In: Proceedings of the 10th IEEE International Conference on Control and Automation. Hangzhou, China: IEEE, 2013. 1441-1446 [33] Yin S, Wei Z L, Gao H J, Peng K X. Data-driven quality related prediction and monitoring. In: Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society. Montreal, Canada: IEEE, 2012. 3874-3879 [34] Peng K X, Zhang K, You B, Dong J. Quality-relevant fault monitoring based on efficient projection to latent structures with application to hot strip mill process. IET Control Theory & Applications, 2015, 9(7): 1135-1145 https://www.researchgate.net/publication/276421361_Brief_paper_Quality-relevant_fault_monitoring_based_on_efficient_projection_to_latent_structures_with_application_to_hot_strip_mill_process [35] Raich A, Çinar A. Statistical process monitoring and disturbance diagnosis in multivariable continuous processes. AIChE Journal, 1996, 42(4): 995-1009 doi: 10.1002/(ISSN)1547-5905 [36] Yoon S, MacGregor J F. Fault diagnosis with multivariate statistical models——Part Ⅰ: using steady state fault signatures. Journal of Process Control, 2001, 11(4): 387-400 doi: 10.1016/S0959-1524(00)00008-1 [37] Kano M, Hasebe S, Hashimoto I, Ohno H. Statistical process monitoring based on dissimilarity of process data. AIChE Journal, 2002, 48(6): 1231-1240 doi: 10.1002/(ISSN)1547-5905 [38] Kano M, Nagao K, Hasebe S, Hashimoto I, Ohno H, Strauss R, Bakshi B R. Comparison of multivariate statistical process monitoring methods with applications to the Eastman challenge problem. Computers & Chemical Engineering, 2002, 26(2): 161-174 http://www.academia.edu/794859/Comparison_of_multivariate_statistical_process_monitoring_methods_with_applications_to_the_Eastman_challenge_problem [39] Qin S J, Li W H. Detection, identification, and reconstruction of faulty sensors with maximized sensitivity. AIChE Journal, 1999, 45(9): 1963-1976 doi: 10.1002/(ISSN)1547-5905 [40] Qin S J, Li W H. Detection and identification of faulty sensors in dynamic processes. AIChE Journal, 2001, 47(7): 1581-1593 doi: 10.1002/(ISSN)1547-5905 [41] Gertler J, Li W H, Huang Y B, McAvoy T. Isolation enhanced principal component analysis. AIChE Journal, 1999, 45(2): 323-334 doi: 10.1002/(ISSN)1547-5905 [42] Zhou Z, Wen C L, Yang C J. Fault isolation based on k-nearest neighbor rule for industrial processes. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2578-2586 [43] Li G, Qin S J, Yuan T. Data-driven root cause diagnosis of faults in process industries. Chemometrics and Intelligent Laboratory Systems, 2016, 159: 1-11 doi: 10.1016/j.chemolab.2016.09.006 [44] He B, Chen T, Yang X H. Root cause analysis in multivariate statistical process monitoring: integrating reconstruction-based multivariate contribution analysis with fuzzy-signed directed graphs. Computers & Chemical Engineering, 2014, 64: 167-177 [45] Liu Q, Chai T Y, Qin S J. Fault diagnosis of continuous annealing processes using a reconstruction-based method. Control Engineering Practice, 2012, 20(5): 511-518 doi: 10.1016/j.conengprac.2012.01.005 [46] Peng K X, Zhang K, Li G, Zhou D H. Contribution rate plot for nonlinear quality-related fault diagnosis with application to the hot strip mill process. Control Engineering Practice, 2013, 21(4): 360-369 doi: 10.1016/j.conengprac.2012.11.013 [47] Peng K X, Zhang K, Li G. Online contribution rate based fault diagnosis for nonlinear industrial processes. Acta Automatica Sinica, 2014, 40(3): 423-430 doi: 10.1016/S1874-1029(14)60005-7 [48] MacGregor J F, Kourti T. Statistical process control of multivariate processes. Control Engineering Practice, 1995, 3(3): 403-414 doi: 10.1016/0967-0661(95)00014-L [49] Miller P, Swanson R E, Heckler C E. Contribution plots: a missing link in multivariate quality control. Applied Mathematics and Computer Science, 1998, 8(4): 775-792 https://www.infona.pl/resource/bwmeta1.element.baztech-article-BPZ1-0021-0043 [50] Louwerse D J, Tates A A, Smilde A K, Koot G L M, Berndt H. PLS discriminant analysis with contribution plots to determine differences between parallel batch reactors in the process industry. Chemometrics and Intelligent Laboratory Systems, 1999, 46(2): 197-206 doi: 10.1016/S0169-7439(98)00185-3 [51] 李钢, 秦泗钊, 吉吟东, 周东华.基于T-PLS贡献图方法的故障诊断技术.自动化学报, 2009, 35(6): 759-765 http://www.aas.net.cn/CN/article/searchArticle.do#Li Gang, Qin Si-Zhao, Ji Yin-Dong, Zhou Dong-Hua. Total PLS based contribution plots for fault diagnosis. Acta Automatica Sinica, 2009, 35(6): 759-765 http://www.aas.net.cn/CN/article/searchArticle.do# [52] Westerhuis J A, Gurden S P, Smilde A K. Generalized contribution plots in multivariate statistical process monitoring. Chemometrics and Intelligent Laboratory Systems, 2000, 51(1): 95-114 doi: 10.1016/S0169-7439(00)00062-9 [53] Conlin A K, Martin E B, Morris A J. Confidence limits for contribution plots. Journal of Chemometrics, 2000, 14(5-6): 725-736 doi: 10.1002/(ISSN)1099-128X [54] Alcala C F, Qin S J. Reconstruction-based contribution for process monitoring. Automatica, 2009, 45(7): 1593-1600 doi: 10.1016/j.automatica.2009.02.027 [55] Alcala C F, Qin S J. Analysis and generalization of fault diagnosis methods for process monitoring. Journal of Process Control, 2011, 21(3): 322-330 doi: 10.1016/j.jprocont.2010.10.005 [56] Dunia R, Qin S J. Subspace approach to multidimensional fault identification and reconstruction. AIChE Journal, 1998, 44(8): 1813-1831 doi: 10.1002/(ISSN)1547-5905 [57] Yue H H, Qin S J. Reconstruction-based fault identification using a combined index. Industrial & Engineering Chemistry Research, 2001, 40(20): 4403-4414 https://www.researchgate.net/publication/280656257_Reconstruction-based_fault_identification_using_a_combined_index [58] Li G, Liu B S, Qin S J, Zhou D H. Quality relevant data-driven modeling and monitoring of multivariate dynamic processes: the dynamic T-PLS approach. IEEE Transactions on Neural Networks, 2011, 22(12): 2262-2271 doi: 10.1109/TNN.2011.2165853 [59] Li G, Qin S J, Chai T Y. Multi-directional reconstruction based contributions for root-cause diagnosis of dynamic processes. In: Proceedings of the 2014 American Control Conference. Portland, OR, USA: IEEE, 2014. 3500-3505 [60] Kaspar M H, Ray W H. Dynamic PLS modelling for process control. Chemical Engineering Science, 1993, 48(20): 3447-3461 doi: 10.1016/0009-2509(93)85001-6 [61] Kaspar M H, Ray W H. Chemometric methods for process monitoring and high-performance controller design. AIChE Journal, 1992, 38(10): 1593-1608 doi: 10.1002/(ISSN)1547-5905 [62] Lakshminarayanan S, Shah S L, Nandakumar K. Modeling and control of multivariable processes: dynamic PLS approach. AIChE Journal, 1997, 43(9): 2307-2322 doi: 10.1002/(ISSN)1547-5905 [63] Ricker N L. The use of biased least-squares estimators for parameters in discrete-time pulse-response models. Industrial & Engineering Chemistry Research, 1988, 27(2): 343-350 https://www.researchgate.net/publication/231368465_The_Use_of_Biased_Least-Sqares_Estimators_for_Parameters_in_Discrete-Time_Pulse_Response_Models [64] Qin S J, McAvoy T J. A data-based process modeling approach and its applications. In: Proceedings of the 3rd IFAC Symposium on Dynamics and Control of Chemical Reactors, Distillation Columns and Batch Processes. Maryland, USA: IFAC, 1992. 93-98 [65] Chen J H, Liu K C. On-line batch process monitoring using dynamic PCA and dynamic PLS models. Chemical Engineering Science, 2002, 57(1): 63-75 doi: 10.1016/S0009-2509(01)00366-9 [66] Lee G, Song S O, Yoon E S. Multiple-fault diagnosis based on system decomposition and dynamic PLS. Industrial & Engineering Chemistry Research, 2003, 42(24): 6145-6154 https://www.researchgate.net/publication/277433117_Multiple-Fault_Diagnosis_Based_on_System_Decomposition_and_Dynamic_PLS [67] Fletcher N M, Morris A J, Montague G, Martin E B. Local dynamic partial least squares approaches for the modelling of batch processes. The Canadian Journal of Chemical Engineering, 2008, 86(5): 960-970 doi: 10.1002/cjce.v86:5 [68] Liu Q, Qin S J, Chai T Y. Quality-relevant monitoring and diagnosis with dynamic concurrent projection to latent structures. In: Proceedings of the 19th IFAC World Congress. Cape Town, South Africa: IFAC, 2014. 2740-2745 [69] Jiao J F, Yu H, Wang G. A quality-related fault detection approach based on dynamic least squares for process monitoring. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2625-2632 https://www.researchgate.net/publication/284113080_A_quality-related_fault_detection_approach_based_on_dynamic_least_squares_for_process_monitoring [70] Helland K, Berntsen H E, Borgen O S, Martens H. Recursive algorithm for partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 1992, 14(1-3): 129-137 doi: 10.1016/0169-7439(92)80098-O [71] Qin S J. Recursive PLS algorithms for adaptive data modeling. Computers & Chemical Engineering, 1998, 22(4-5): 503-514 https://www.researchgate.net/publication/222476094_Recursive_PLS_Algorithms_for_Adaptive_Data_Modeling [72] Dong J, Zhang K, Huang Y, Li G, Peng K X. Adaptive total PLS based quality-relevant process monitoring with application to the Tennessee Eastman process. Neurocomputing, 2015, 154: 77-85 doi: 10.1016/j.neucom.2014.12.017 [73] Wang Y, Seborg D E, Larimore W E. Process monitoring based on canonical variate analysis. In: Proceedings of the 1997 European Control Conference. Brussels: IEEE, 1997. 3089-3094 [74] Jiang B B, Huang D X, Zhu X X, Yang F, Braatz R D. Canonical variate analysis-based contributions for fault identification. Journal of Process Control, 2015, 26: 17-25 doi: 10.1016/j.jprocont.2014.12.001 [75] 曹玉苹, 黄琳哲, 田学民.一种基于DIOCVA的过程监控方法.自动化学报, 2015, 41(12): 2072-2080 http://www.aas.net.cn/CN/abstract/abstract18780.shtmlCao Yu-Ping, Huang Lin-Zhe, Tian Xue-Min. A process monitoring method using dynamic input-output canonical variate analysis. Acta Automatica Sinica, 2015, 41(12): 2072-2080 http://www.aas.net.cn/CN/abstract/abstract18780.shtml [76] Wold S, Kettaneh-Wold N, Skagerberg B. Nonlinear PLS modeling. Chemometrics and Intelligent Laboratory Systems, 1989, 7(1-2): 53-65 doi: 10.1016/0169-7439(89)80111-X [77] Qin S J, McAvoy T J. Nonlinear PLS modeling using neural networks. Computers & Chemical Engineering, 1992, 16(4): 379-391 [78] Malthouse E C, Tamhane A C, Mah R S H. Nonlinear partial least squares. Computers & Chemical Engineering, 1997, 21(8): 875-890 [79] Lindgren F, Geladi P, Wold S. The kernel algorithm for PLS. Journal of Chemometrics, 1993, 7(1): 45-59 doi: 10.1002/(ISSN)1099-128X [80] Zhang Y W, Zhou H, Qin S J, Chai T Y. Decentralized fault diagnosis of large-scale processes using multiblock kernel partial least squares. IEEE Transactions on Industrial Informatics, 2010, 6(1): 3-10 doi: 10.1109/TII.2009.2033181 [81] Peng K X, Zhang K, Li G. Quality-related process monitoring based on total kernel PLS model and its industrial application. Mathematical Problems in Engineering, 2013, 2013: Article ID 707953 [82] Zhao X Q, Xue Y F. Output-relevant fault detection and identification of chemical process based on hybrid kernel T-PLS. The Canadian Journal of Chemical Engineering, 2014, 92(10): 1822-1828 doi: 10.1002/cjce.v92.10 [83] Mori J, Yu J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach. Journal of Process Control, 2014, 24(1): 57-71 doi: 10.1016/j.jprocont.2013.10.017 [84] Zhang Y W, Sun R R, Fan Y P. Fault diagnosis of nonlinear process based on KCPLS reconstruction. Chemometrics and Intelligent Laboratory Systems, 2015, 140: 49-60 doi: 10.1016/j.chemolab.2014.10.002 [85] Zhang Y W, Du W Y, Fan Y P, Zhang L J. Process Fault detection using directional kernel partial least squares. Industrial & Engineering Chemistry Research, 2015, 54(9): 2509-2518 https://www.researchgate.net/publication/273903960_Process_Fault_Detection_Using_Directional_Kernel_Partial_Least_Squares [86] Luo L J, Bao S Y, Mao J F, Tang D. Quality prediction and quality-relevant monitoring with multilinear PLS for batch processes. Chemometrics and Intelligent Laboratory Systems, 2016, 150: 9-22 doi: 10.1016/j.chemolab.2015.11.004 [87] Liu Y, Chang Y Q, Wang F L. Nonlinear dynamic quality-related process monitoring based on dynamic total kernel PLS. In: Proceeding of the 11th World Congress on Intelligent Control and Automation. Shenyang, China: IEEE, 2014. 1360-1365 [88] Jia Q L, Zhang Y W. Quality-related fault detection approach based on dynamic kernel partial least squares. Chemical Engineering Research and Design, 2016, 106: 242-252 doi: 10.1016/j.cherd.2015.12.015 [89] 邓晓刚, 田学民.基于核规范变量分析的非线性故障诊断方法.控制与决策, 2006, 21(10): 1109-1113 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200610005.htmDeng Xiao-Gang, Tian Xue-Min. Nonlinear process fault diagnosis based on kernel canonical variate analysis. Control and Decision, 2006, 21(10): 1109-1113 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200610005.htm [90] Tan S, Wang F L, Chang Y Q, Chen W D, Xu J Z. Fault detection and diagnosis of nonlinear processes based on kernel ICA-KCCA. In: Proceeding of the 2010 Chinese Control and Decision Conference. Xuzhou, China: IEEE, 2010. 3869-3874 [91] Samuel R T, Cao Y. Kernel canonical variate analysis for nonlinear dynamic process monitoring. IFAC-PapersOnLine, 2015, 48(8): 605-610 doi: 10.1016/j.ifacol.2015.09.034 [92] Hwang D H, Han C H. Real-time monitoring for a process with multiple operating modes. Control Engineering Practice, 1999, 7(7): 891-902 doi: 10.1016/S0967-0661(99)00038-6 [93] Lane S, Martin E B, Kooijmans R, Morris A J. Performance monitoring of a multi-product semi-batch process. Journal of Process Control, 2001, 11(1): 1-11 doi: 10.1016/S0959-1524(99)00063-3 [94] Zhao S J, Zhang J, Xu Y M. Performance monitoring of processes with multiple operating modes through multiple PLS models. Journal of Process Control, 2006, 16(7): 763-772 doi: 10.1016/j.jprocont.2005.12.002 [95] Yue H H, Qin S J, Wiseman J, Toprac A. Plasma etching endpoint detection using multiple wavelengths for small open-area wafers. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films, 2001, 19(1): 66-75 https://www.researchgate.net/publication/249508451_Plasma_etching_endpoint_detection_using_multiple_wavelengths_for_small_open-area_wafers [96] Yu J, Qin S J. Multiway Gaussian mixture model based multiphase batch process monitoring. Industrial & Engineering Chemistry Research, 2009, 48(18): 8585-8594 https://www.researchgate.net/publication/231390559_Multiway_Gaussian_Mixture_Model_Based_Multiphase_Batch_Process_Monitoring [97] Yoo C K, Villez K, Lee I B, Rosén C, Vanrolleghem P A. Multi-model statistical process monitoring and diagnosis of a sequencing batch reactor. Biotechnology and Bioengineering, 2007, 96(4): 687-701 doi: 10.1002/(ISSN)1097-0290 [98] Peng K X, Zhang K, You B, Dong J. Quality-related prediction and monitoring of multi-mode processes using multiple PLS with application to an industrial hot strip mill. Neurocomputing, 2015, 168: 1094-1103 doi: 10.1016/j.neucom.2015.05.014 [99] Nomikos P, MacGregor J F. Multi-way partial least squares in monitoring batch processes. Chemometrics and Intelligent Laboratory Systems, 1995, 30(1): 97-108 doi: 10.1016/0169-7439(95)00043-7 [100] Kouti T, Nomikos P, MacGregor J F. Analysis, monitoring and fault diagnosis of batch processes using multiblock and multiway PLS. Journal of Process Control, 1995, 5(4): 277-284 doi: 10.1016/0959-1524(95)00019-M [101] Chen J H, Cheng Y C. Applying partial least squares based decomposition structure to multiloop adaptive proportional-integral-derivative controllers in nonlinear processes. Industrial & Engineering Chemistry Research, 2004, 43(18): 5888-5898 [102] Ündey C, Ertunç S, Çinar A. Online batch/fed-batch process performance monitoring, quality prediction, and variable-contribution analysis for diagnosis. Industrial & Engineering Chemistry Research, 2003, 42(20): 4645-4658 [103] Facco P, Doplicher F, Bezzo F, Barolo M. Moving average PLS soft sensor for online product quality estimation in an industrial batch polymerization process. Journal of Process Control, 2009, 19(3): 520-529 doi: 10.1016/j.jprocont.2008.05.002 [104] Wang D. Robust data-driven modeling approach for real-time final product quality prediction in batch process operation. IEEE Transactions on Industrial Informatics, 2011, 7(2): 371-377 doi: 10.1109/TII.2010.2103401 [105] Stubbs S, Zhang J, Morris J. Multiway interval partial least squares for batch process performance monitoring. Industrial & Engineering Chemistry Research, 2013, 52(35): 12399-12407 doi: 10.1021/ie303562t [106] Peng K X, Zhang K, You B, Dong J, Wang Z D. A quality-based nonlinear fault diagnosis framework focusing on industrial multimode batch processes. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2615-2624 https://www.researchgate.net/publication/291556261_A_Quality-Based_Nonlinear_Fault_Diagnosis_Framework_Focusing_on_Industrial_Multimode_Batch_Processes [107] Kesavan P, Lee J H, Saucedo V, Krishnagopalan G A. Partial least squares (PLS) based monitoring and control of batch digesters. Journal of Process Control, 2000, 10(2-3): 229-236 doi: 10.1016/S0959-1524(99)00028-1 [108] Ündey C, Çinar A. Statistical monitoring of multistage, multiphase batch processes. IEEE Control Systems Magazine, 2002, 22(5): 40-52 doi: 10.1109/MCS.2002.1035216 [109] Zhao C H. Concurrent phase partition and between-mode statistical analysis for multimode and multiphase batch process monitoring. AIChE Journal, 2014, 60(2): 559-573 doi: 10.1002/aic.14282 [110] Zhao C H, Wang F L, Lu N Y, Jia M X. Stage-based soft-transition multiple PCA modeling and on-line monitoring strategy for batch processes. Journal of Process Control, 2007, 17(9): 728-741 doi: 10.1016/j.jprocont.2007.02.005 [111] 赵春晖, 王福利, 姚远, 高福荣.基于时段的间歇过程统计建模、在线监测及质量预报.自动化学报, 2010, 36(3): 366-374 doi: 10.3724/SP.J.1004.2010.00366Zhao Chun-Hui, Wang Fu-Li, Yao Yuan, Gao Fu-Rong. Phase-based statistical modeling, online monitoring and quality prediction for batch processes. Acta Automatica Sinica, 2010, 36(3): 366-374 doi: 10.3724/SP.J.1004.2010.00366 [112] Lu N Y, Gao F R. Stage-based online quality control for batch processes. Industrial & Engineering Chemistry Research, 2006, 45(7): 2272-2280 https://www.researchgate.net/publication/231373310_Stage-Based_Online_Quality_Control_for_Batch_Processes [113] Russell S A, Kesavan P, Lee J H, Ogunnaike B A. Recursive data-based prediction and control of batch product quality. AIChE Journal, 1998, 44(11): 2442-2458 doi: 10.1002/(ISSN)1547-5905 [114] Pan Y D, Lee J H. Recursive data-based prediction and control of product quality for a PMMA batch process. Chemical Engineering Science, 2003, 58(14): 3215-3221 doi: 10.1016/S0009-2509(03)00190-8 [115] Kaistha N, Johnson M S, Moore C F, Leitnaker M G. Online batch recipe adjustments for product quality control using empirical models: application to a nylon-66 process. ISA Transactions, 2003, 42(2): 305-315 doi: 10.1016/S0019-0578(07)60135-9 -





 下载:
下载: