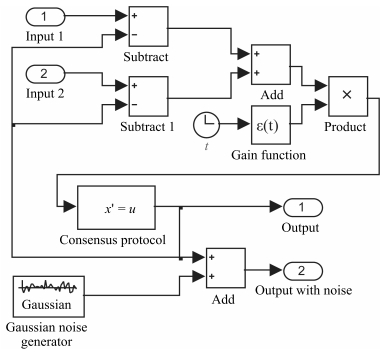
-
摘要: 多智能体协同在传感网、社交网、分布式控制等诸多领域有着广泛的实际应用背景,一致性问题作为多智能体协同的基础,受到越来越多研究者的关注.在实际环境中,由于设备、通信干扰等诸多原因,信息在传递过程中通常会携有噪声,本文对噪声条件下一致性问题的系统偏差进行了研究,将求解一致性协议噪声偏差问题转化成矩阵范数的积分问题,根据矩阵迹与特征值的关系,利用范数不等式及积分中值定理,给出仅与增益函数和网络结构相关的一致性协议噪声偏差上界,为一致性系统在实际应用中的噪声估计奠定了理论基础.Abstract: Multi-agent cooperation has found applications in many fields such as sensor network, social network, distributed control, etc. The consistency problem is the basis for multi-agent cooperation, and receives much attention from more and more researchers. In real circumstances, because of equipment and communication interference, the information often carries noise during the transfer process. The paper studies the system deviation of consistency problem under noise condition, and the solution of noise deviation problem under consistency protocol is transformed into the integral of matrix norm. According to the relationship of trace and eigenvalue of the matrix, and based on the norm inequation and mean value theorem of integrals, the upper bound of noise deviation under consistency protocol which is only related with gain function and network structure is given, which establishes a theoretical basis for noise evaluation of consistent systems in real application.1) 本文责任编委 吕金虎
-
表 1 Lstar所有非零特征值
Table 1 All nonzero eigenvalues of Lstar
λi (Lstar) i = 2 i = 3 i = 4 i = 5 i = 6 i = 7 i = 8 1.00 1.00 1.00 1.00 1.00 1.00 8.00 表 2 Lpath所有非零特征值
Table 2 All nonzero eigenvalues of Lpath
λi (Lpath) i = 2 i = 3 i = 4 i = 5 i = 6 i = 7 i = 8 0.152 0.586 1.235 2.000 2.765 3.414 3.848 表 3 Lcircle所有非零特征值
Table 3 All nonzero eigenvalues of Lcircle
λi (Lcircle) i = 2 i = 3 i = 4 i = 5 i = 6 i = 7 i = 8 0.586 0.586 2.000 2.000 3.414 3.414 4.000 表 4 Lcircle_N4所有非零特征值
Table 4 All nonzero eigenvalues of Lcircle_N4
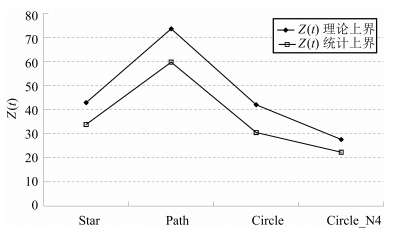
λi (Lcircle_N4) i = 2 i = 3 i = 4 i = 5 i = 6 i = 7 i = 8 2.586 2.586 4.000 5.414 5.414 6.000 6.000 表 5 Z(t) 理论上界与统计值的数据对比
Table 5 The detailed comparison of theoretical upper bound and statistical results of Z(t)
网络结构 Star Path Circle Circle_N4 Z(t)理论上界 42.875 73.512 41.999 27.619 Z(t)统计值 33.856 59.689 30.518 22.335 -
[1] Reynolds C W. Flocks, herds and schools:a distributed behavioral model. In:Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. New York, USA:ACM, 1987. 25-34 [2] Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel type of phase transition in a system of self-driven particles. Physical Review Letters, 1995, 75(6):1226-1229 doi: 10.1103/PhysRevLett.75.1226 [3] Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):988-1001 doi: 10.1109/TAC.2003.812781 [4] Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 2007, 95(1):215-233 doi: 10.1109/JPROC.2006.887293 [5] Olfati-Saber R. Evolutionary dynamics of behavior in social networks. In:Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, LA, USA:IEEE, 2007. 4051-4056 [6] Olfati-Saber R, Jalalkamali P. Coupled distributed estimation and control for mobile sensor networks. IEEE Transactions on Automatic Control, 2012, 57(10):2609-2614 doi: 10.1109/TAC.2012.2190184 [7] Olfati-Saber R. Flocking for multi-agent dynamic systems:algorithms and theory. IEEE Transactions on Automatic Control, 2006, 51(3):401-420 doi: 10.1109/TAC.2005.864190 [8] Yu C H. Biologically-Inspired Control for Self-Adaptive Multiagent Systems[Ph.D. dissertation], Harvard University, USA, 2010. [9] Yu C H, Nagpal R. Biologically-inspired control for multi-agent self-adaptive tasks. In:Proceedings of the 24th AAAI Conference on Artificial Intelligence. Atlanta, USA:AAAI, 2010. 1702-1707 [10] Yu C H, Nagpal R. A self-adaptive framework for modular robots in a dynamic environment:theory and applications. The International Journal of Robotics Research, 2011, 30(8):1015-1036 doi: 10.1177/0278364910384753 [11] Li Z K, Duan Z S, Chen G R, Huang L. Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2010, 57(1):213-224 doi: 10.1109/TCSI.2009.2023937 [12] Li Z, Duan Z, Chen G. Dynamic consensus of linear multi-agent systems. IET Control Theory and Applications, 2011, 5(1):19-28 doi: 10.1049/iet-cta.2009.0466 [13] Li Z K, Liu X D, Ren W, Xie L H. Distributed tracking control for linear multiagent systems with a leader of bounded unknown input. IEEE Transactions on Automatic Control, 2013, 58(2):518-523 doi: 10.1109/TAC.2012.2208295 [14] Wen G H, Duan Z S, Li Z K, Chen G R. Consensus and its L2-gain performance of multi-agent systems with intermittent information transmissions. International Journal of Control, 2012, 85(4):384-396 doi: 10.1080/00207179.2011.654264 [15] Wen G H, Duan Z S, Li Z K, Chen G R. Flocking of multi-agent dynamical systems with intermittent nonlinear velocity measurements. International Journal of Robust and Nonlinear Control, 2012, 22(16):1790-1805 doi: 10.1002/rnc.v22.16 [16] Tran T M D, Kibangou A. Distributed design of finite-time average consensus protocols. In:Proceedings of the 4th IFAC Workshop on Distributed Estimation and Control in Networked Systems. Rhine Moselle Hall, Koblenz, Germany:IFAC, 2013. 227-233 [17] Huang M Y, Manton J H. Coordination and consensus of networked agents with noisy measurements:stochastic algorithms and asymptotic behavior. SIAM Journal on Control and Optimization, 2009, 48(1):134-161 doi: 10.1137/06067359X [18] Huang M Y, Manton J H. Stochastic consensus seeking with noisy and directed inter-agent communication:fixed and randomly varying topologies. IEEE Transactions on Automatic Control, 2010, 55(1):235-241 doi: 10.1109/TAC.2009.2036291 [19] Liu S, Xie L H, Zhang H S. Distributed consensus for multi-agent systems with delays and noises in transmission channels. Automatica, 2011, 47(5):920-934 doi: 10.1016/j.automatica.2011.02.003 [20] 窦全胜, 丛玲, 姜平, 史忠植.离散线性一致性算法噪声问题研究.自动化学报, 2015, 41(7):1328-1340 http://www.aas.net.cn/CN/abstract/abstract18706.shtmlDou Quan-Sheng, Cong Ling, Jiang Ping, Shi Zhong-Zhi. Research on discrete linear consensus algorithm with noises. Acta Automatica Sinica, 2015, 41(7):1328-1340 http://www.aas.net.cn/CN/abstract/abstract18706.shtml [21] Garin F, Schenato L. A survey on distributed estimation and control applications using linear consensus algorithms. Networked Control Systems. London:Springer, 2010. 75-107 [22] 闵海波, 刘源, 王仕成, 孙富春.多个体协调控制问题综述.自动化学报, 2012, 38(10):1557-1570 http://www.aas.net.cn/CN/abstract/abstract17765.shtmlMin Hai-Bo, Liu Yuan, Wang Shi-Cheng, Sun Fu-Chun. An overview on coordination control problem of multi-agent system. Acta Automatica Sinica, 2012, 38(10):1557-1570 http://www.aas.net.cn/CN/abstract/abstract17765.shtml [23] Young G F, Scardovi L, Leonard N E. Robustness of noisy consensus dynamics with directed communication. In:Proceedings of the 2010 American Control Conference. Baltimore, MD, USA:IEEE, 2010. 6312-6317 -




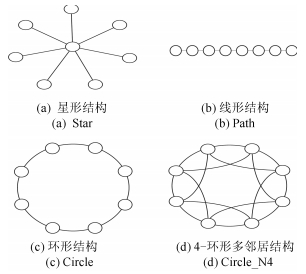
 下载:
下载: