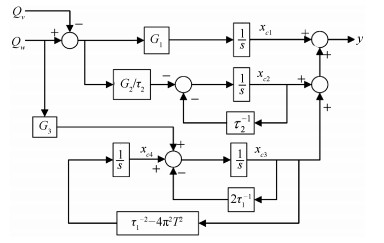
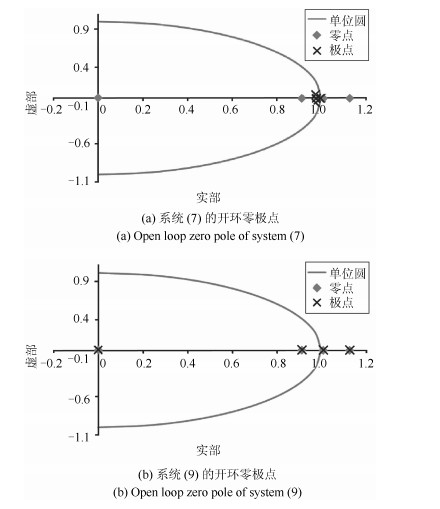
Soft Constrained MPC on Water Level Control in Steam Generator of a Nuclear Power Plant
-
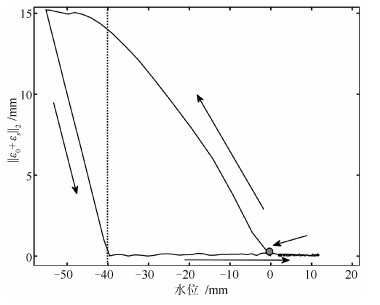
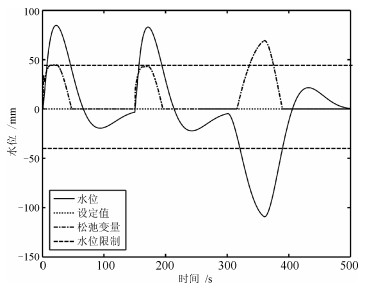
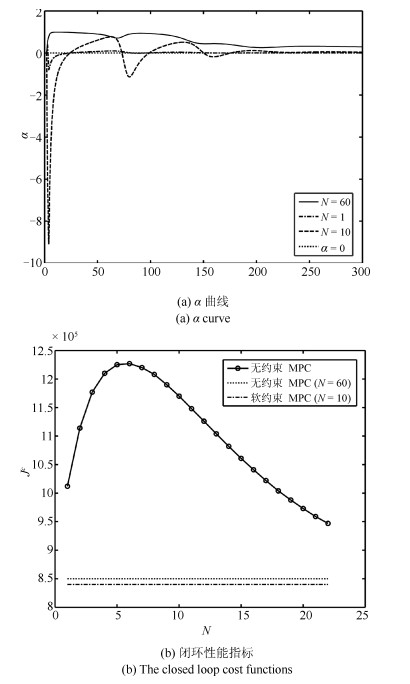
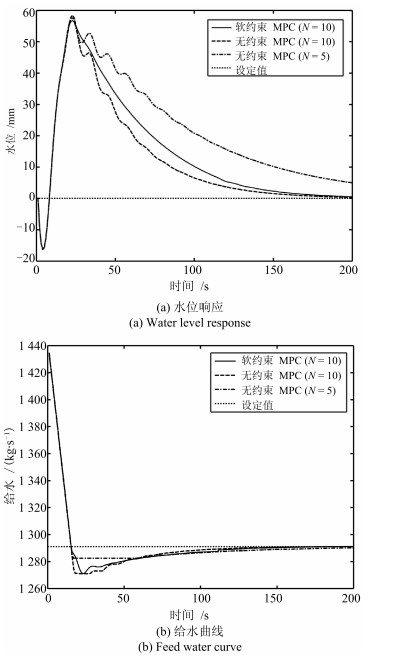
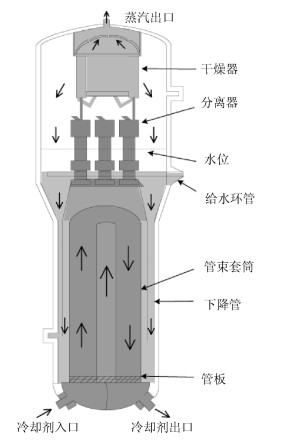
摘要: 核电站的蒸汽发生器(U-tube steam generator,UTSG)水位控制对核反应堆安全运行至关重要.模型预测控制(Model predictive control,MPC)具有内在的约束处理能力,是UTSG水位控制的有效方法.然而在大范围变功率情况下,水位硬约束会降低水位的控制性能,甚至导致系统不稳定.本文基于UTSG的分段线性输入输出模型,设计了水位软约束MPC.离线计算终端约束集,减少在线计算量,保证稳定性;引入两种松弛变量来放宽水位约束和终端约束集;在蒸汽流量扰动和功率变化情况下的仿真结果表明了算法的有效性.Abstract: In the nuclear power plant, the water level control of the U-tube steam generator (UTSG) plays a vital role on the safety of the nuclear reactor operation. Model predictive control (MPC) has been a quite effective way of controlling the water level of UTSG, due to its water level constraint handling ability. However, when the nuclear power plant is working under wide load changing condition, the water level hard constraint may deteriorate the closed-loop control performance and even cause instability. This paper presents a soft constrained MPC on the UTSG water level control based on the linear parameter varying (LPV) model. A terminal constraint set is computed off-line to reduce the online computation burden and ensure stability. Slack variables are introduced in the MPC formulation to relax the water level and terminal constraint in a straightforward way. Simulations under both the steam disturbance and the power-level changing show the effectiveness of the proposed controllers.
-
Key words:
- Model predictive control /
- soft constraint /
- steam generator /
- non-minimum phase system
1) 本文责任编委 梅生伟 -
表 1 软约束MPC计算量
Table 1 The computation of soft constrained MPC
状态个数 控制量个数 控制时域 决策变量个数 等式约束个数 不等式约束个数 最小时间 最大时间 平均时间 5 1 10 32 50 86 90 ms 302 ms 147 ms -
[1] 张小冬, 刘琳. AP 1000反应堆控制系统特点分析.核动力工程, 2011, 32(4):62-65 http://d.old.wanfangdata.com.cn/Periodical/hdlgc201104014Zhang Xiao-Dong, Liu Lin. Analysis of AP 1000 reactor power control system. Nuclear Power Engineering, 2011, 32(4):62-65 http://d.old.wanfangdata.com.cn/Periodical/hdlgc201104014 [2] Parlos A G, Rais O T. Nonlinear control of U-tube steam generators via H∞ control. Control Engineering Practice, 2000, 8(8):921-936 doi: 10.1016/S0967-0661(00)00020-4 [3] Dong Z, Huang X J, Feng J T. Water-level control for the U-tube steam generator of nuclear power plants based on output feedback dissipation. IEEE Transactions on Nuclear Science, 2009, 56(3):1600-1612 doi: 10.1109/TNS.2009.2019593 [4] Wei L, Fang F, Shi Y. Adaptive backstepping-based composite nonlinear feedback water level control for the nuclear U-tube steam generator. IEEE Transactions on Control Systems Technology, 2014, 22(1):369-377 doi: 10.1109/TCST.2013.2250504 [5] 陈红, 曾建, 王广军.蒸汽发生器水位的自抗扰控制.中国电机工程学报, 2010, 30(32):103-107 http://d.old.wanfangdata.com.cn/Periodical/zgdl201406018Chen Hong, Zeng Jian, Wang Guang-Jun. Steam generator water level control based on active disturbances rejection control. Proceedings of the CSEE, 2010, 30(32):103-107 http://d.old.wanfangdata.com.cn/Periodical/zgdl201406018 [6] 席裕庚, 李德伟, 林姝.模型预测控制——现状与挑战.自动化学报, 2013, 39(3):222-236 http://www.aas.net.cn/CN/abstract/abstract17874.shtmlXi Yu-Geng, Li De-Wei, Lin Shu. Model predictive control-status and challenges. Acta Automatica Sinica, 2013, 39(3):222-236 http://www.aas.net.cn/CN/abstract/abstract17874.shtml [7] 柴天佑, 李少远, 王宏.网络信息模式下复杂工业过程建模与控制.自动化学报, 2013, 39(5):469-470 http://www.aas.net.cn/CN/abstract/abstract17922.shtmlChai Tian-You, Li Shao-Yuan, Wang Hong. Modeling and control for complex industrial processes in networked information. Acta Automatica Sinica, 2013, 39(5):469-470 http://www.aas.net.cn/CN/abstract/abstract17922.shtml [8] Qi S J, Badgwell T A. A survey of industrial model predictive control technology. Control Engineering Practice, 2003, 11(7):733-764 doi: 10.1016/S0967-0661(02)00186-7 [9] 刘向杰, 孔小兵.电力工业复杂系统模型预测控制——现状与发展.中国电机工程学报, 2013, 33(5):79-85 http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201305012Liu Xiang-Jie, Kong Xiao-Bing. Present situation and prospect of model predictive control application in complex power industrial process. Proceedings of the CSEE, 2013, 33(5):79-85 http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201305012 [10] 孔小兵, 刘向杰.永磁同步电机高效非线性模型预测控制.自动化学报, 2014, 40(9):1958-1966 http://www.aas.net.cn/CN/abstract/abstract18466.shtmlKong Xiao-Bing, Liu Xiang-Jie. Efficient nonlinear model predictive control for permanent magnet synchronous motor. Acta Automatica Sinica, 2014, 40(9):1958-1966 http://www.aas.net.cn/CN/abstract/abstract18466.shtml [11] 郑毅, 李少远.网络信息模式下分布式系统协调预测控制.自动化学报, 2013, 39(11):1778-1786 http://www.aas.net.cn/CN/abstract/abstract18217.shtmlZheng Yi, Li Shao-Yuan. Networked cooperative distributed model predictive control for dynamic coupling systems. Acta Automatica Sinica, 2013, 39(11):1778-1786 http://www.aas.net.cn/CN/abstract/abstract18217.shtml [12] 朱宇轩, 李少远.双层模型预测控制系统的多包镇定域分析与系统设计.自动化学报, 2018, 44(2):262-269 http://www.aas.net.cn/CN/abstract/abstract19221.shtmlZhu Yu-Xuan, Li Shao-Yuan. Analysis and system design of multi-convex hull stabilization domain for double-layered model predictive control system. Acta Automatica Sinica, 2018, 44(2):262-269 http://www.aas.net.cn/CN/abstract/abstract19221.shtml [13] 杨亚茹, 李少远.切换非线性系统全局优化运行的经济预测控制.自动化学报, 2017, 43(6):1017-1027 http://www.aas.net.cn/CN/abstract/abstract19077.shtmlYang Ya-Ru, Li Shao-Yuan. Economic model predictive control for global optimal operation of nonlinear switching systems. Acta Automatica Sinica, 2017, 43(6):1017-1027 http://www.aas.net.cn/CN/abstract/abstract19077.shtml [14] Kothare M V, Mettler B, Morari M, Bendotti P, Falinower C M. Level control in the steam generator of a nuclear power plant. IEEE Transactions on Control Systems Technology, 2000, 8(1):55-69 doi: 10.1109/87.817692 [15] Hu K, Yuan J Q. Multi-model predictive control method for nuclear steam generator water level. Energy Conversion and Management, 2008, 49(5):1167-1174 doi: 10.1016/j.enconman.2007.09.006 [16] 姜頔, 刘向杰.核电站蒸汽发生器水位模糊预测控制.控制理论与应用, 2015, 32(12):1705-1712 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201512019Jiang Di, Liu Xiang-Jie. Fuzzy-model predictive control on water level of U-tube steam generator. Control Theory & Applications, 2015, 32(12):1705-1712 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201512019 [17] Kavaklioglu K. Support vector regression model based predictive control of water level of U-tube steam generators. Nuclear Engineering and Design, 2014, 278:651-660 doi: 10.1016/j.nucengdes.2014.08.018 [18] Rawlings J B, Muske K R. The stability of constrained receding horizon control. IEEE Transactions on Automatic Control, 1993, 38(10):1512-1516 doi: 10.1109/9.241565 [19] Scokaert P O M, Rawlings J B. Feasibility issues in linear model predictive control. AIChE Journal, 1999, 45(8):1649-1659 doi: 10.1002/(ISSN)1547-5905 [20] Zeilinger M N, Morari M, Jones C N. Soft constrained model predictive control with robust stability guarantees. IEEE Transactions on Automatic Control, 2014, 59(5):1190-1202 doi: 10.1109/TAC.2014.2304371 [21] Irving E, Miossec C, Tassart J. Towards efficient full automatic operation of the pwr steam generator with water level adaptive control. In:Proceedings of the 2nd International Conforence Boiler Dynamics and Control in Nuclear Power Stations. London, UK:British Nuclear Energy Society, 1980. 309-329 [22] Mayne D Q, Rawlings J B, Rao C V, Scokaert P O M. Constrained model predictive control:stability and optimality. Automatica, 2000, 36(6):789-814 doi: 10.1016/S0005-1098(99)00214-9 [23] Limon D, Alvarado I, Alamo T, Camacho E F. MPC for tracking piecewise constant references for constrained linear systems. Automatica, 2008, 44(9):2382-2387 doi: 10.1016/j.automatica.2008.01.023 [24] Andersen E D, Roos C, Terlaky T. On implementing a primal-dual interior-point method for conic quadratic optimization. Mathematical Programming, 2003, 95(2):249-277 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6ee9470592d05af0170c016fb2fa7237 -




 下载:
下载: