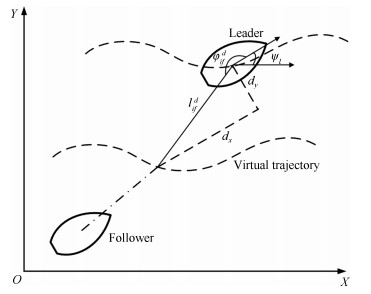
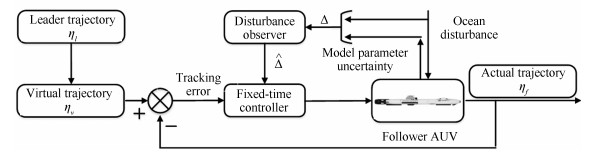
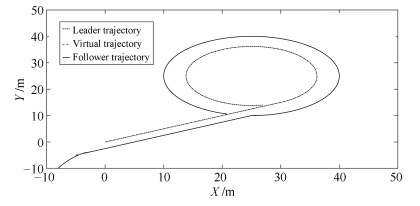
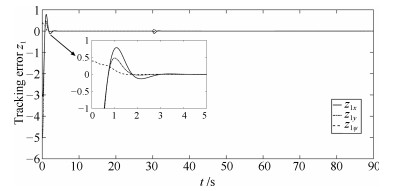
-
摘要: 考虑含有模型参数不确定及未知海洋扰动的多AUVs协同编队问题，本文提出一种新的控制方法，该方法可保证编队在固定时间内实现.首先，将模型参数不确定及海洋扰动看作复合扰动，设计扰动观测器，实现固定时间内对扰动的精确估计.基于扰动观测器，指令滤波技术、固定时间理论及虚拟轨迹概念，设计编队控制律，实现编队目标，并保证闭环系统中的所有信号是全局固定时间稳定的.最后通过两艘AUV的编队仿真验证了所提算法的有效性.Abstract: The paper is concerned with formation control of autonomous underwater vehicles (AUVs) subject to model parameter uncertainties and unknown ocean disturbances, a novel control scheme is developed, by which the formation can be achieved within a fixed time. The ocean disturbance is combined with the model parameter uncertainties as a compound disturbance. Then a disturbance observer (DO) is constructed to estimate the compound disturbance, which can be achieved within the settling time with zero estimation errors. Based on the DO, command filter technique, fixed-time control and virtual trajectory, a formation control law is designed, by which the formation control can be achieved with all the states globally stabilized in a given fixed time. The effectiveness of the proposed control scheme is demonstrated by numerical simulations.
-
Key words:
- Disturbance observer /
- formation control /
- multi-AUVs /
- fixed-time control /
- virtual trajectory
1) 本文责任编委 刘艳军 -
图 4 领航AUV轨迹、虚拟轨迹及跟随AUV轨迹
Fig. 4 Trajectory of leader, virtual trajectory and trajectory of follower
图 5 跟随AUV轨迹与虚拟轨迹跟踪误差$z_1$
Fig. 5 Tracking error $z_1$ between follower trajectory and virtual trajectory
图 9 复合干扰$\varDelta$及其观测值$\hat{\varDelta}$
Fig. 9 Compound disturbance $\varDelta$ and its estimate $\hat{\varDelta}$
图 10 复合扰动$\varDelta$及其观测值$\hat{\varDelta}$
Fig. 10 Compound disturbance $\varDelta$ and its estimate $\hat{\varDelta}$
图 11 领航AUV轨迹、虚拟轨迹及不同初始状态下跟随AUV轨迹
Fig. 11 Trajectory of leader, virtual trajectory and trajectory of follower under different initial states
图 12 不同初始状态下跟随AUV轨迹与虚拟轨迹位置及航向跟踪误差$z_1$
Fig. 12 Tracking error $z_1$ between follower trajectory and virtual trajectory with different initial states
表 1 AUV模型参数
Table 1 Parameters of AUV
Symbol Value Unit $m$ 185 kg $X_u$ $-$70 kg/s $Y_v$ $-$100 kg/s $N_r$ $-$50 $\text{kgm}^2$ $X_{\dot{u}}$ $-$30 kg $Y_{\dot{v}}$ $-$80 kg $N_{\dot{r}}$ $-$30 $\text{kgm}^2$ $X_{u|u|}$ $-$100 kg/m $Y_{|v|v}$ $-$200 kg/m $N_{|r|r}$ $-$100 $\text{kgm}^2$ $I_z$ 50 $\text{kgm}^2$ 
下载: 导出CSV
-
[1] 王宏健, 陈子印, 贾鹤鸣, 李娟, 陈兴华.基于滤波反步法的欠驱动AUV三维路径跟踪控制.自动化学报, 2015, 41(3): 631-645 http://www.aas.net.cn/CN/abstract/abstract18640.shtmlWang Hong-Jian, Chen Zi-Yin, Jia He-Ming, Li Juan, Chen Xing-Hua. Three-dimensional path-following control of underactuated autonomous underwater vehicle with command filtered backstepping. Acta Automatica Sinica, 2015, 41(3): 631-645 http://www.aas.net.cn/CN/abstract/abstract18640.shtml [2] Peng Z, Wang D, Wang H, Wang W. Distributed coordinated tracking of multiple autonomous underwater vehicles. Nonlinear Dynamics, 2014, 78(2): 1261-1276 doi: 10.1007/s11071-014-1513-z [3] Ali F, Kim E K, Kim Y G. Type-2 fuzzy ontology-based semantic knowledge for collision avoidance of autonomous underwater vehicles. Information Sciences, 2015, 295: 441-464 doi: 10.1016/j.ins.2014.10.013 [4] Rizzini D L, Kallasi F, Aleotti J, Oleari F, Caselli S. Integration of a stereo vision system into an autonomous underwater vehicle for pipe manipulation tasks. Computers & Electrical Engineering, 2017, 58: 560-571 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c20d9bd1b72535e40b984ab3ac93b6e1 [5] Elhaki O, Shojaei K. Neural network-based target tracking control of underactuated autonomous underwater vehicles with a prescribed performance. Ocean Engineering, 2018, 167: 239-256 doi: 10.1016/j.oceaneng.2018.08.007 [6] Sun P, Boukerche A. Modelling and analysis of coverage degree and target detection for autonomous underwater vehicle-based system. IEEE Transactions on Vehicular Technology, 2018, 67(10): 9959-9971 doi: 10.1109/TVT.2018.2864141 [7] Hu Z, Ma C, Zhang L. Formation control of impulsive networked autonomous underwater vehicles under fixed and switching topologies. Neurocomputing, 2015, 147: 291-298 doi: 10.1016/j.neucom.2014.06.060 [8] Gao Z, Guo G. Adaptive formation control of autonomous underwater vehicles with model uncertainties. International Journal of Adaptive Control and Signal Processing, 2018, 32(7): 1067-1080 doi: 10.1002/acs.v32.7 [9] Gao Z, Guo G. Fixed-time leader-follower formation control of autonomous underwater vehicles with event-triggered intermittent communications. IEEE Access, 2018, 6: 27902-27911 doi: 10.1109/ACCESS.2018.2838121 [10] Park B S. Adaptive formation control of underactuated autonomous underwater vehicles. Ocean Engineering, 2015, 96: 1-7 doi: 10.1016/j.oceaneng.2014.12.016 [11] Shojaei, K. Neural network formation control of underactuated autonomous underwater vehicles with saturating actuators. Neurocomputing, 2016, 194: 372-384 doi: 10.1016/j.neucom.2016.02.041 [12] 李乐强, 王银涛.模型参数不确定条件下的自主水下航行器(AUV)自适应编队控制研究.舰船电子工程, 2015, 1: 154-157 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jcdzgc201501040Li Le-Qiang, Wang Yin-Tao. Adaptive formation control of AUVs in the presence of parametric model uncertainty. Ship Electronic Engineering, 2015, 1: 154-157 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jcdzgc201501040 [13] Yang Y, Du J, Liu H, Guo C, Abraham A. A trajectory tracking robust controller of surface vessels with disturbance uncertainties. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1511-1518 doi: 10.1109/TCST.2013.2281936 [14] Wang N, Qian C, Sun J C, Liu Y C. Adaptive robust finite-time trajectory tracking control of fully actuated marine surface vehicles. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1454-1462 doi: 10.1109/TCST.2015.2496585 [15] 张国庆, 黄晨峰, 吴晓雪, 张显库.考虑伺服系统增益不确定的船舶动力定位自适应有限时间控制.自动化学报, 2018, 44(10): 1907-1912 http://www.aas.net.cn/CN/abstract/abstract19372.shtmlZhang Guo-Qing, Huang Chen-Feng, Wu Xiao-Xue, Zhang Xian-Ku. Adaptive finite time dynamic positioning control of fully-actuated ship with servo system uncertainties. Acta Automatica Sinica, 2018, 44(10): 1907-1912 http://www.aas.net.cn/CN/abstract/abstract19372.shtml [16] Ye H, Li M, Yang C, Gui W. Finite-time stabilization of the double integrator subject to input saturation and input delay. IEEE/CAA Journal of Automatica Sinica, 2018, 5(5): 1017-1024 doi: 10.1109/JAS.2018.7511177 [17] Tian B, Zuo Z, Yan X, Wang H. A fixed-time output feedback control scheme for double integrator systems. Automatica, 2017, 80: 17-24 doi: 10.1016/j.automatica.2017.01.007 [18] Polyakov A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Transactions on Automatic Control, 2012, 57(8): 2106-2110 doi: 10.1109/TAC.2011.2179869 [19] Farrell J A, Polycarpou M, Sharma M. Command filtered backstepping. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395 doi: 10.1109/TAC.2009.2015562 -
计量
- 文章访问数: 2661
- HTML全文浏览量: 398
- PDF下载量: 665
- 被引次数: 0
