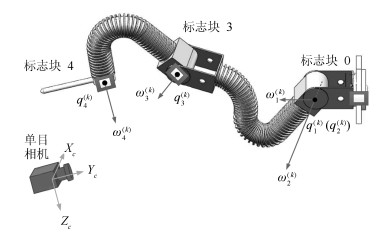
-
摘要: 针对家庭服务机器人工作的非结构化环境, 本文设计了一种可以根据任务需求相应地调整连杆形状的可变形操作臂.该操作臂工作空间易于拓展、灵活度较高且成本低廉.但连杆形状的改变给操作臂的建模和控制带来了困难.首先, 可变形臂的运动学参数发生了巨大且无规律的变化, 使得固结在操作臂连杆上的关节坐标系可能脱离操作臂本体, 变得不可测量.其次, 为适应不同任务需求, 可变形臂的连杆形状需要经常改变, 而传统标定方法往往追求更高的标定精度而非标定效率.最后, 可变形臂的标定方法必须低成本且易于在家庭环境中实施, 而基于激光等传感器的标定方法设备价格昂贵, 对实验环境要求严格, 不便于在家庭中实施.因此, 一种廉价、快速、易于实施的标定方法是可变形臂应用的基础.本文分别基于Denavit-Hartenberg(DH)模型和旋量模型提出了基于视觉标志块间相对位姿测量的标定算法, 该算法在标志块处建立虚拟关节, 通过测量不同标志块间的相对位姿可快速、高效地获取可变形臂的运动学参数.实验说明了两种标定方法的有效性, 同时还表明旋量模型更适合可变形臂的建模.最后, 本文给出了利用可变形臂进行点触任务操作的实例, 展示出可变形操作臂在家庭使用中的优势.
-
关键词:
- 可变形操作臂 /
- 运动学 /
- Denavit-Hartenberg表示法 /
- 旋量 /
- 操作臂标定
Abstract: The deformable manipulator can obtain relatively dexterous end-effector and extended workspace with fewer joints by bending its deformable links.However, frequent changes in links's shape may bring difficulties to the model and control of the manipulator.The reasons are as follows.First, the kinematic parameters experience drastic changes and become totally unknown.It is hard to measure the parameters directly.Second, the change is frequent.Thus a low-cost, less time consuming calibration method is the fundament of deformable manipulator for home service robots.In this paper, two calibration methods based on relative pose measurement of visual markers are developed for the Denavit-Hartenberg (DH) model and screw theory model, respectively.By introducing a virtual joint at the marker, the method can calculate the kinematic parameters quickly according to the relative pose of visual markers.Experimental results verify the effectiveness of the methods.It is shown that the screw model is more suitable for the deformable manipulator.Finally, two point touching tasks are conducted to demonstrate the advantage of the deformable manipulator.-
Key words:
- Deformable manipulator /
- kinematics /
- Denavit-Hartenberg (DH) /
- screw theory /
- calibration
1) 本文责任编委 侯增广 -
图 1 可变形连杆发生形变后对DH参数的影响
Fig. 1 The change in DH parameters caused by the deformable link
图 2 可变形连杆发生形变后对旋量参数的影响
Fig. 2 The change in screw parameters caused by the deformable link
图 4 可变形操作臂和传统刚性臂的工作空间与不同任务空间的重合度比较
Fig. 4 Comparison of the deformable and rigid manipulator facing two task spaces
图 5 具有两个可变形连杆的四自由度操作臂及其标定系统
Fig. 5 A deformable manipulator with four DOFs and two deformable links and its calibration system
图 7 第$k$个臂形下可变形操作臂DH模型示意图
Fig. 7 DH model of the deformable manipulator in\\ the $k$-th configuration
图 8 基于旋量理论的可变形操作臂运动学模型
Fig. 8 Kinematics model of the deformable manipulator based on screw theory
图 9 可变形操作臂参数标定的实验平台
Fig. 9 Experimental platform for parameters calibration of the deformable manipulator
图 10 可变形操作臂点触任务实验设置
Fig. 10 The experiments setup for the deformable manipulator in touching tasks
图 11 传统臂形下进行点触任务作业仿真实验
Fig. 11 The simulation of touching tasks by deformable manipulator in traditional configuration
表 1 可变形操作臂DH参数表
Table 1 DH parameters of the deformable manipulator
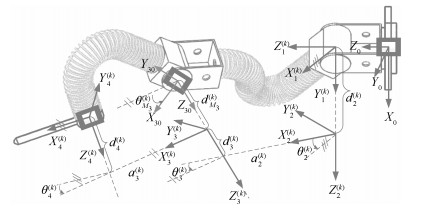
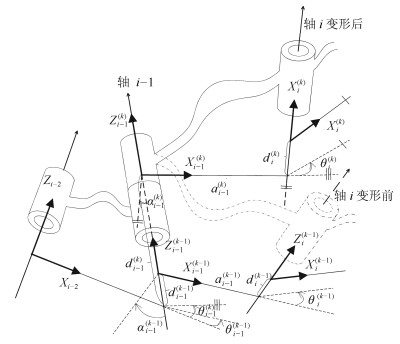
$i$ ${\alpha _{i - 1}}$ ${a_{i - 1}}$ ${\theta _{i}}$ ${d _{i}}$ 1 0 0 ${\theta _{1}}$ $d _{1}$ 2 $-\pi /2$ 0 ${\theta_{2}}+\Delta \theta _{2}$ $d _{2}$ 3 ${\alpha _2}$ ${a _2}$ ${\theta _{3}}+\Delta\theta _{3}$ $d _{3}$ 4 ${\alpha _3}$ ${a _3}$ ${\theta _{4}}+\Delta\theta _{4}$ $d _{4}$ $w$ 0 $L_w$ 0 0 
下载: 导出CSV
表 2 第$k$个臂形下虚拟操作臂的DH模型参数表
Table 2 DH parameters of the virtual manipulator in the $k$-th configuration
$i^{\left(k\right)}$ ${\alpha _{i - 1}^{\left(k\right)}}$ ${a_{i - 1}^{\left(k\right)}}$ ${\theta _{i}^{\left(k\right)}}$ ${d _{i}^{\left(k\right)}}$ 1 0 0 ${\theta _{1}}$ $d _{1}$ 2 $-\pi /2$ 0 $\theta _2 + \underline {{\Delta \theta _{2}^{\left(k\right)}}}$ $\underline {{d _{2}^{\left(k\right)}}}$ 3 $\underline{{\alpha _{2}^{\left(k\right)}}}$ $\underline{{a _{2}^{\left(k\right)}}}$ $\theta _3 + \underline {{\Delta \theta _{3}^{\left(k\right)}} + {\theta _{M_3}^{\left(k\right)}}}$ $\underline {{d_{3}^{\left(k\right)}} + {d_{M_3}^{\left(k\right)}} } $ 4 $\underline {{\alpha _{3}^{\left(k\right)}}} $ $\underline {{a_{3}^{\left(k\right)}}} $ $\theta _4 + \underline {{\Delta \theta _{4}^{\left(k\right)}} - {\theta _{M_3}^{\left(k\right)}}} $ $\underline {{d_{4}^{\left(k\right)}} - {d_{M_3}^{\left(k\right)}} } $ $w$ 0 $L_w$ 0 0
下载: 导出CSV
表 3 可变形操作臂第$k$个臂形的参数标定的初值的结果
Table 3 The raw calibration results of the deformable manipulator in the $k$-th configuration
$i^{\left(k\right)}$ ${\alpha _{i - 1}^{\left(k\right)}}$ ${a_{i - 1}^{\left(k\right)}}$ ${\theta _{i}^{\left(k\right)}}$ ${d _{i}^{\left(k\right)}}$ $1$ 0 0 ${\theta _{1}}$ $d _{1}$ $2$ $-90^{\circ}$ 0 $\theta _{2}+(\underline {{-2.81^{\circ}}})$ $\underline {-150.60}$ $3$ $\underline{-81.97^{\circ}}$ $\underline{269.46}$ $\theta _{3}+(\underline {-7.28^{\circ}})$ $\underline {-116.54} $ $4$ $\underline {138.73^{\circ}} $ $\underline {160.08} $ $\theta _{4}+(\underline {-109.26^{\circ}})$ $\underline {29.13} $ $w$ 0 $Lw$ 0 0
下载: 导出CSV
表 4 可变形臂DH参数标定的初值的位姿误差
Table 4 Pose errors of the deformable manipulator based on raw calibrated DH parameters
误差类型 误差分量 位置误差(mm) $39.95 \pm 12.82$ $X$ $-13.54 \pm 13.41$ $Y$ $26.54 \pm 7.76$ $Z$ $19.17 \pm 16.57$ 欧拉角姿态误差$(^\circ)$ $4.66\pm 0.86$ $\alpha$ $-0.30 \pm 0.36$ $\beta$ $0.66 \pm 0.33$ $\gamma$ $3.61 \pm 0.62$
下载: 导出CSV
表 5 可变形臂旋量模型参数标定的初值的位姿误差
Table 5 Pose errors of the deformable manipulator based on raw calibrated screw parameters
误差类型 误差分量 位置误差(mm) $39.57 \pm 22.31$ $X$ $-30.61 \pm 24.13$ $Y$ $4.21 \pm 14.83$ $Z$ $-4.88 \pm 17.31$ 欧拉角姿态误差$(^{\circ})$ $0.25 \pm 0.18$ $\alpha$ $0.09 \pm 0.17$ $\beta$ $0.05 \pm 0.08$ $\gamma$ $-0.03 \pm 0.04$
下载: 导出CSV
表 6 传统臂形下进行点触任务作业仿真实验
Table 6 The simulation of touching tasks by deformable manipulator in traditional configuration
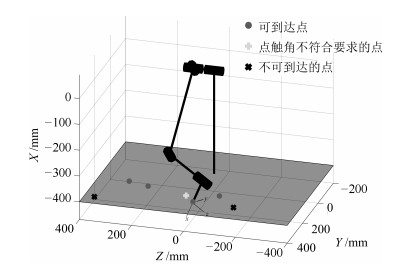
序号 点触目标点$\left({\rm mm}\right)$ 有效点触位姿点触角$\alpha$ $\left(^\circ \right)$ 1 $\left(-400.0, 280.0, -2.0\right)^{\rm T}$ 23.17 2 $\left(-400.0, 200.0, -80.0\right)^{\rm T}$ 17.77 3 $\left(-400.0, 160.0, 280.0\right)^{\rm T}$ 2.97 4 $\left(-400.0, 185.0, 200.0\right)^{\rm T}$ 18.17 5 $\left(-400.0, 230.0, 40.0\right)^{\rm T}$ 无解$\left(29.76\right)$ 6 $\left(-400.0, 290.0, -160.0\right)^{\rm T}$ 无解 7 $\left(-400.0, 340.0, 360.0\right)^{\rm T}$ 无解
下载: 导出CSV
-
[1] 黄云天, 陈卫东, 孙逸翔.基于碰撞检测的护理型操作臂的安全性设计与实现.机器人, 2011, 33(1):40-45 http://d.old.wanfangdata.com.cn/Periodical/jqr201101007Huang Yun-Tian, Chen Wei-Dong, Sun Yi-Xiang.Safety design and realization of an assistive robotic manipulator based on collision detection.Robot, 2011, 33(1):40-45 http://d.old.wanfangdata.com.cn/Periodical/jqr201101007 [2] Li Z J, Chen W D.Adaptive neural-fuzzy control of uncertain constrained multiple coordinated nonholonomic mobile manipulators.Engineering Applications of Artificial Intelligence, 2008, 21(7):985-1000 doi: 10.1016/j.engappai.2007.08.007 [3] Rusu R B, Holzbach A, Diankov R, Bradski G, Beetz M. Perception for mobile manipulation and grasping using active stereo. In: Proceedings of the 9th IEEE-RAS International Conference on Humanoid Robots. Paris, France: IEEE, 2009. 632-638 [4] Cianchetti M, Follador M, Mazzolai B, Dario P, Laschi C. Design and development of a soft robotic octopus arm exploiting embodied intelligence. In: Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, Minnesota, USA: IEEE, 2012. 5271-5276 [5] Guglielmino E, Zullo L, Cianchetti M, Follador M, Branson D, Caldwell D G. The application of embodiment theory to the design and control of an octopus-like robotic arm. In: Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, Minnesota, USA: IEEE, 2012. 5277-5282 [6] Mahl T, Hildebrandt A, Sawodny O.A variable curvature continuum kinematics for kinematic control of the bionic handling assistant.IEEE Transactions on Robotics, 2014, 30(4):935-949 doi: 10.1109/TRO.2014.2314777 [7] Calisti M, Arienti A, Renda F, Levy G, Hochner B, Mazzolai B, Dario P, Laschi C. Design and development of a soft robot with crawling and grasping capabilities. In: Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, Minnesota, USA: IEEE, 2012. 4950-4955 [8] Escande C, Chettibi T, Merzouki R, Coelen V, Pathak P M.Kinematic calibration of a multisection bionic manipulator.IEEE/ASME Transactions on Mechatronics, 2015, 20(2):663-674 doi: 10.1109/TMECH.2014.2313741 [9] Jones B A, Walker I D.Kinematics for multisection continuum robots.IEEE Transactions on Robotics, 2006, 22(1):43-55 doi: 10.1109/TRO.2005.861458 [10] Escande C, Pathak P M, Merzouki R, Coelen V. Modelling of multisection bionic manipulator: application to robotinoXT. In: Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics (ROBIO). Karon Beach, Phuket, Thailand: IEEE, 2011. 92-97 [11] Bergeles C, Gosline A H, Vasilyev N V, Codd P J, Nido P J, Dupont P E.Concentric tube robot design and optimization based on task and anatomical constraints.IEEE Transactions on Robotics, 2015, 31(1):67-84 doi: 10.1109/TRO.2014.2378431 [12] Dupont P E, Lock J, Itkowitz B. Real-time position control of concentric tube robots. In: Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA). Anchorage, Alaska, USA: IEEE, 2010. 562-568 [13] Gilbert H B, Neimat J, Webster R J.Concentric tube robots as steerable needles:achieving follow-the-leader deployment.IEEE Transactions on Robotics, 2015, 31(2):246-258 doi: 10.1109/TRO.2015.2394331 [14] Rucker D C, Jones B A, Webster R J. A model for concentric tube continuum robots under applied wrenches. In: Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA). Anchorage, Alaska, USA: IEEE, 2010. 1047-1052 [15] 郭宪, 马书根, 李斌, 王明辉, 王越超.基于动力学与控制统一模型的蛇形机器人速度跟踪控制方法研究.自动化学报, 2015, 41(11):1847-1856 http://www.aas.net.cn/CN/abstract/abstract18760.shtmlGuo Xian, Ma Shu-Gen, Li Bin, Wang Ming-Hui, Wang Yue-Chao.Velocity tracking control of a snake-like robot with a dynamics and control unified model.Acta Automatica Sinica, 2015, 41(11):1847-1856 http://www.aas.net.cn/CN/abstract/abstract18760.shtml [16] 杨贵志, 马书根, 李斌, 王明辉.面向蛇形机器人的三维步态控制的层次化联结中枢模式生成器模型.自动化学报, 2013, 39(10):1611-1622 http://www.aas.net.cn/CN/abstract/abstract18198.shtmlYang Gui-Zhi, Ma Shu-Gen, Li Bin, Wang Ming-Hui.A hierarchical connectionist central pattern generator model for controlling three-dimensional gaits of snake-like robots.Acta Automatica Sinica, 2013, 39(10):1611-1622 http://www.aas.net.cn/CN/abstract/abstract18198.shtml [17] 王智锋, 马书根, 李斌, 王越超.基于能量的蛇形机器人蜿蜒运动控制方法的仿真与实验研究.自动化学报, 2011, 37(5):604-614 http://www.aas.net.cn/CN/abstract/abstract17396.shtmlWang Zhi-Feng, Ma Shu-Gen, Li Bin, Wang Yue-Chao.Simulation and experimental study of an energy-based control method for the serpentine locomotion of a snake-like robot.Acta Automatica Sinica, 2011, 37(5):604-614 http://www.aas.net.cn/CN/abstract/abstract17396.shtml [18] Yip M C, Camarillo D B.Model-less feedback control of continuum manipulators in constrained environment.IEEE Transactions on Robotics, 2014, 30(4):880-889 doi: 10.1109/TRO.2014.2309194 [19] Wang H S, Chen W D, Yu X J, Deng T, Wang X Z, Pfeifer R. Visual servo control of cable-driven soft robotic manipulator. In: Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Tokyo, Japan: IEEE, 2013. 57-62 [20] 陈炜, 余跃庆, 张绪平, 苏丽颖.欠驱动柔性机器人的振动可控性分析.自动化学报, 2007, 33(4):391-398 http://www.aas.net.cn/CN/abstract/abstract13859.shtmlChen Wei, Yu Yue-Qing, Zhang Xu-Ping, Su Li-Ying.Vibration controllability of underactuated flexible manipulator.Acta Automatica Sinica, 2007, 33(4):391-398 http://www.aas.net.cn/CN/abstract/abstract13859.shtml [21] 彭济根, 倪远华, 乔红.柔性关节机操手的神经网络控制.自动化学报, 2007, 33(2):175-180 http://www.aas.net.cn/CN/abstract/abstract13826.shtmlPeng Ji-Gen, Ni Yuan-Hua, Qiao Hong.Neural network control of flexible-joint robot manipulators.Acta Automatica Sinica, 2007, 33(2):175-180 http://www.aas.net.cn/CN/abstract/abstract13826.shtml [22] Santolaria J, Aguilar J J, Yagüe J A, Pastor J.Kinematic parameter estimation technique for calibration and repeatability improvement of articulated arm coordinate measuring machines.Precision Engineering, 2008, 32(4):251-268 doi: 10.1016/j.precisioneng.2007.09.002 [23] Park I W, Lee B J, Cho S H, Hong Y D, Kim J H.Laser-based kinematic calibration of robot manipulator using differential kinematics.IEEE/ASME Transactions on Mechatronics, 2012, 17(6):1059-1067 doi: 10.1109/TMECH.2011.2158234 [24] Angelidis A, Vosniakos G C.Prediction and compensation of relative position error along industrial robot end-effector paths.International Journal of Precision Engineering and Manufacturing, 2014, 15(1):63-73 doi: 10.1007/s12541-013-0306-5 [25] Majarena A C, Santolaria J, Samper D, Aguilar J J.An overview of kinematic and calibration models using internal/external sensors or constraints to improve the behavior of spatial parallel mechanisms.Sensors, 2010, 10(11):10256-10297 doi: 10.3390/s101110256 [26] 郝洁. 家庭服务机器人可变形操作臂的运动学研究[硕士学位论文], 南开大学, 中国, 2015.Hao J. Research on Kinematics of Deformable Manipulator for Home Service Robots[Master thesis], Nankai University, China, 2015. [27] Lu X, Liu J T, Hao J, Zhang S, Sun L. Self-calibration of deformable arm with a monocular camera. In: Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO). Bali, Indonesia, 2014. 861-866 [28] 卢翔. 单目目标识别及位姿测量算法研究与应用[博士学位论文], 南开大学, 中国, 2015.Lu Xiang. Research and Application on Object Recognition and Pose Measurement Based on Monocular Camera[Ph. D. dissertation], Nankai University, China, 2015. [29] Li G, Sun L, Lu X, Hao J, Liu J T. A practical, fast, and low-cost kinematic calibration scheme for a deformable manipulator by using leap motion. In: Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO). Qingdao, China, 2016. 719-724 [30] Nubiola A, Bonev I A.Absolute robot calibration with a single telescoping ballbar.Precision Engineering, 2014, 38(3):472-480 doi: 10.1016/j.precisioneng.2014.01.001 [31] Mittendorfer P, Cheng G. Open-loop self-calibration of articulated robots with artificial skins. In: Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, Minnesota, USA, 2012. 4539-4545 [32] Roth Z, Mooring B, Ravani B.An overview of robot calibration.IEEE Journal on Robotics and Automation, 1987, 3(5):377-385 doi: 10.1109/JRA.1987.1087124 [33] Lightcap C, Hamner S, Schmitz T, Banks S.Improved positioning accuracy of the PA10-6CE robot with geometric and flexibility calibration.IEEE Transactions on Robotics, 2008, 24(2):452-456 doi: 10.1109/TRO.2007.914003 [34] He R B, Zhao Y J, Yang S N, Yang S Z.Kinematic-parameter identification for serial-robot calibration based on POE formula.IEEE Transactions on Robotics, 2010, 26(3):411-423 doi: 10.1109/TRO.2010.2047529 [35] Chen G L, Wang H, Lin Z Q.Determination of the identifiable parameters in robot calibration based on the POE formula.IEEE Transactions on Robotics, 2014, 30(5):1066-1077 doi: 10.1109/TRO.2014.2319560 [36] Wang H X, Shen S H, Lu X.A screw axis identification method for serial robot calibration based on the POE model.Industrial Robot, 2012, 39(2):146-153 doi: 10.1108/01439911211201609 [37] Chen I M, Yang G L, Tan C T, Yeo S H.Local POE model for robot kinematic calibration.Mechanism and Machine Theory, 2001, 36(11-12):1215-1239 doi: 10.1016/S0094-114X(01)00048-9 [38] Okamura K, Park F C.Kinematic calibration using the product of exponentials formula.Robotica, 1996, 14(4):415-421 doi: 10.1017/S0263574700019810 [39] Gupta K.Kinematic analysis of manipulators using the zero reference position description.The International Journal of Robotics Research, 1986, 5(2):5-13 doi: 10.1177/027836498600500202 [40] Kazerounian K, Qian G Z.Kinematic calibration of robotic manipulator.Journal of Mechanisms, Transmissions, and Automation in Design, 1989, 111(4):482-487 doi: 10.1115/1.3259025 [41] Craig J J.Introduction to Robotics:Mechanics and Control.Upper Saddle River, NJ, USA:Pearson Education International, 2005.62-76 [42] Murray R M, Li Z, Sastry S S.A Mathematical Introduction to Robotic Manipulation.Boca Raton, FL, USA:CRC Press, 1994.52-54 -
点击查看大图
计量
- 文章访问数: 2404
- HTML全文浏览量: 279
- PDF下载量: 480
- 被引次数: 0
