基于Koopman特征核的工业时频因果时延推理网络

翁若昊; 郝矿荣; 陈磊; 丁贺; 刘肖燕

doi:10.16383/j.aas.c240810

基于Koopman特征核的工业时频因果时延推理网络

doi: 10.16383/j.aas.c240810 cstr: 32138.14.j.aas.c240810

翁若昊^{1, 2,},
郝矿荣^{1, 2,},
陈磊^{1, 2,},
丁贺^{1, 2,},
刘肖燕^{1, 2,}

1.
东华大学信息科学与技术学院上海 201620
2.
东华大学数字化纺织服装技术教育部工程研究中心上海 201620

基金项目: 中央高校基本科研业务费专项资金(2232021A-10), 上海市扬帆计划 (22YF1401300)资助

详细信息

作者简介:
翁若昊：东华大学信息科学与技术学院硕士研究生. 主要研究方向为因果推理, 工业过程时序建模和机器学习. E-mail: 2232138@mail.dhu.edu.cn

郝矿荣：博士, 东华大学信息科学与技术学院教授. 1995年获得法国巴黎国家路桥学校数学与计算机科学专业博士学位. 主要研究方向为神经网络, 图像处理, 智能控制, 流程工业的数字化与智能化. 本文通信作者. E-mail: krhao@dhu.edu.cn

陈磊：博士, 东华大学信息科学与技术学院副教授. 主要研究方向为过程控制, 系统辨识, 工业大数据分析. E-mail: leichen@dhu.edu.cn

丁贺：东华大学信息科学与技术学院博士研究生. 2020年获得东华大学自动化专业学士学位. 主要研究方向为不变表征学习与工业过程的时序预测. E-mail: 2211866@mail.dhu.edu.cn

刘肖燕：博士, 东华大学信息科学与技术学院高级实验师. 主要研究方向为智能仿真与优化. E-mail: liuxy@dhu.edu.cn

计量
- 文章访问数: 107
- HTML全文浏览量: 93
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-27
- 网络出版日期: 2025-07-11
- 刊出日期: 2025-08-01

Koopman Feature Kernel-based Time-frequency Causal and Delay Inference Network for Industrial Systems

WENG Ruo-Hao^{1, 2
,},
HAO Kuang-Rong^{1, 2
,},
CHEN Lei^{1, 2
,},
DING He^{1, 2
,},
LIU Xiao-Yan^{1, 2
,}

1.
College of Information Science and Technology, Donghua University, Shanghai 201620
2.
Engineering Research Center of Digitized Textile and Apparel Technology, Ministry of Education, Donghua University, Shanghai 201620

Funds: Supported by Fundamental Research Funds for the Central Universities (2232021A-10) and Shanghai Sailing Program (22YF1401300)

More Information

Author Bio:
WENG Ruo-Hao　Master student at the College of Information Science and Technology, Donghua University. His research interest covers causal inference, time-series modeling in industrial processes, and machine learning

HAO Kuang-Rong　Ph.D., full professor at the College of Information Science and Technology, Donghua University. She received her Ph.D. degree in mathematics and computer science from Ecole Nationale des Ponts et Chaussées, Paris, France in 1995. Her research interest covers neural networks, image processing, intelligent control, and digitalization and intelligence of process industry. Corresponding author of this paper

CHEN Lei　Ph.D., associate professor at the College of Information Science and Technology, Donghua University. Her research interest covers process control, system identification, and industrial big data analysis

DING He　Ph.D. candidate at the College of Information Science and Technology, Donghua University. He received his bachelor degree in automation from Donghua University in 2020. His research interest covers invariant representation learning and time-series prediction for industrial processes

LIU Xiao-Yan　Ph.D., senior experimentalist at the College of Information Science and Technology, Donghua University. Her research interest covers intelligent simulation and optimization

摘要

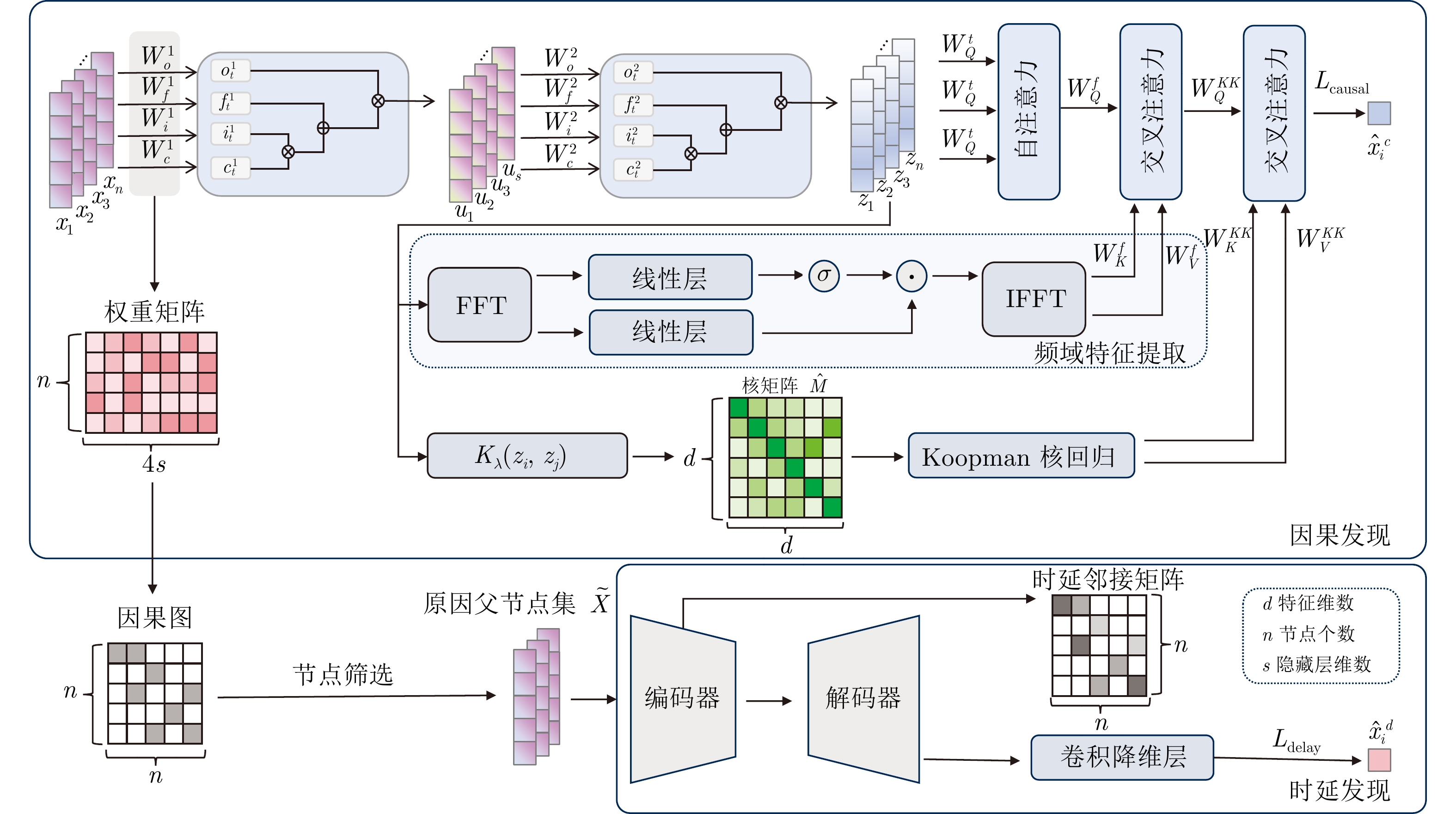
摘要: 因果推理在复杂工业系统中对产能分析和产出优化具有重要意义. 然而, 现有方法难以有效处理这种高度非线性和时延的复杂因果关系. 为此, 提出一种基于Koopman特征核的时频因果与时延推理网络, 用于复杂工业过程的因果分析与时延识别. 该方法结合Koopman特征变换与再生核理论设计核回归层, 在保留时间信息的基础上, 将数据映射到高维再生核希尔伯特空间以提取时不变的非线性关系. 同时, 通过证明非线性格兰杰因果关系在时频域上的一致性, 进而在时域上融入频域特征以提取时间维度的全局信息并捕获变量间的时延关系. 此外, 针对长时延问题, 设计基于状态空间模型的时延发现网络. 实验结果表明, 该方法在三个公共数据集上表现优异, 并在聚酯纤维酯化过程的实际应用中进一步验证了其有效性.
- 因果推理 /
- 工业系统 /
- 再生核希尔伯特空间 /
- 状态空间模型
Abstract: Causal inference plays a crucial role in capacity analysis and output optimization in complex industrial systems. However, existing methods struggle to effectively address highly nonlinear and time-delayed complex causal relationships. To address this, a Koopman feature kernel-based time-frequency causal and delay inference network is proposed for causal analysis and delay identification in complex industrial processes. This method combines Koopman feature transformation and reproducing kernel theory to design a kernel regression layer. By preserving temporal information, it maps data into a high-dimensional reproducing kernel Hilbert space to extract time-invariant nonlinear relationships. Meanwhile, by proving the consistency of nonlinear Granger causality in both time and frequency domains, the method integrates frequency-domain features in the time domain to extract global temporal information and capture time-delay relationships between variables. Furthermore, a time-delay discovery network based on a state-space model is designed to address the challenge of long time delays. Experimental results demonstrate that this method achieves outstanding performance on three public datasets and its effectiveness has been further validated in the practical applications of the polyester fiber esterification process.
- Causal inference /
- industial system /
- reproducing kernel Hilbert space /
- state space model

HTML全文

图 1 第$ i$个KTFCDN结构

Fig. 1 The i-th KTFCDN structure

下载: 全尺寸图片幻灯片

图 2 不同的$ \gamma $值对应的各数据集因果发现F1分数

Fig. 2 F1 scores of causal discovery for different datasets corresponding to different values of $ \gamma $

下载: 全尺寸图片幻灯片

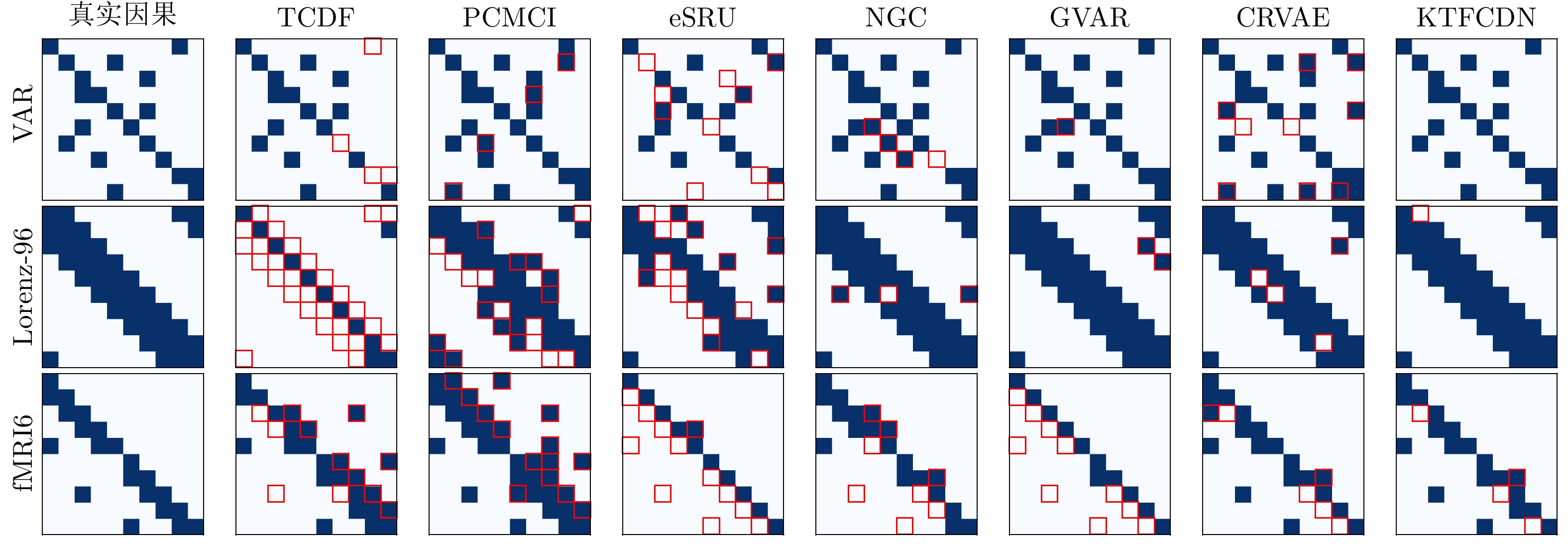
图 3 因果邻接矩阵 (第1列提供了真实因果的可视化, 其余列提供了由因果发现方法发现的因果图, 错误的因果关系用红色的方框标注)

Fig. 3 Causal adjacency matrices (the first column provides a visualization of the ground truth causal relationships, while the others present the causal graphs discovered by causal discovery methods, incorrect causal relationships are highlighted with red boxes)

下载: 全尺寸图片幻灯片

图 4 聚酯纤维生产酯化阶段工艺方案

Fig. 4 Process scheme for esterification stage of polyester fiber production

下载: 全尺寸图片幻灯片

图 5 比较不同预测步数预测指标收敛情况

Fig. 5 Comparison of convergence of prediction metrics with different prediction steps

下载: 全尺寸图片幻灯片

表 1 因果发现比较实验

Table 1 Causal discovery comparison experiment

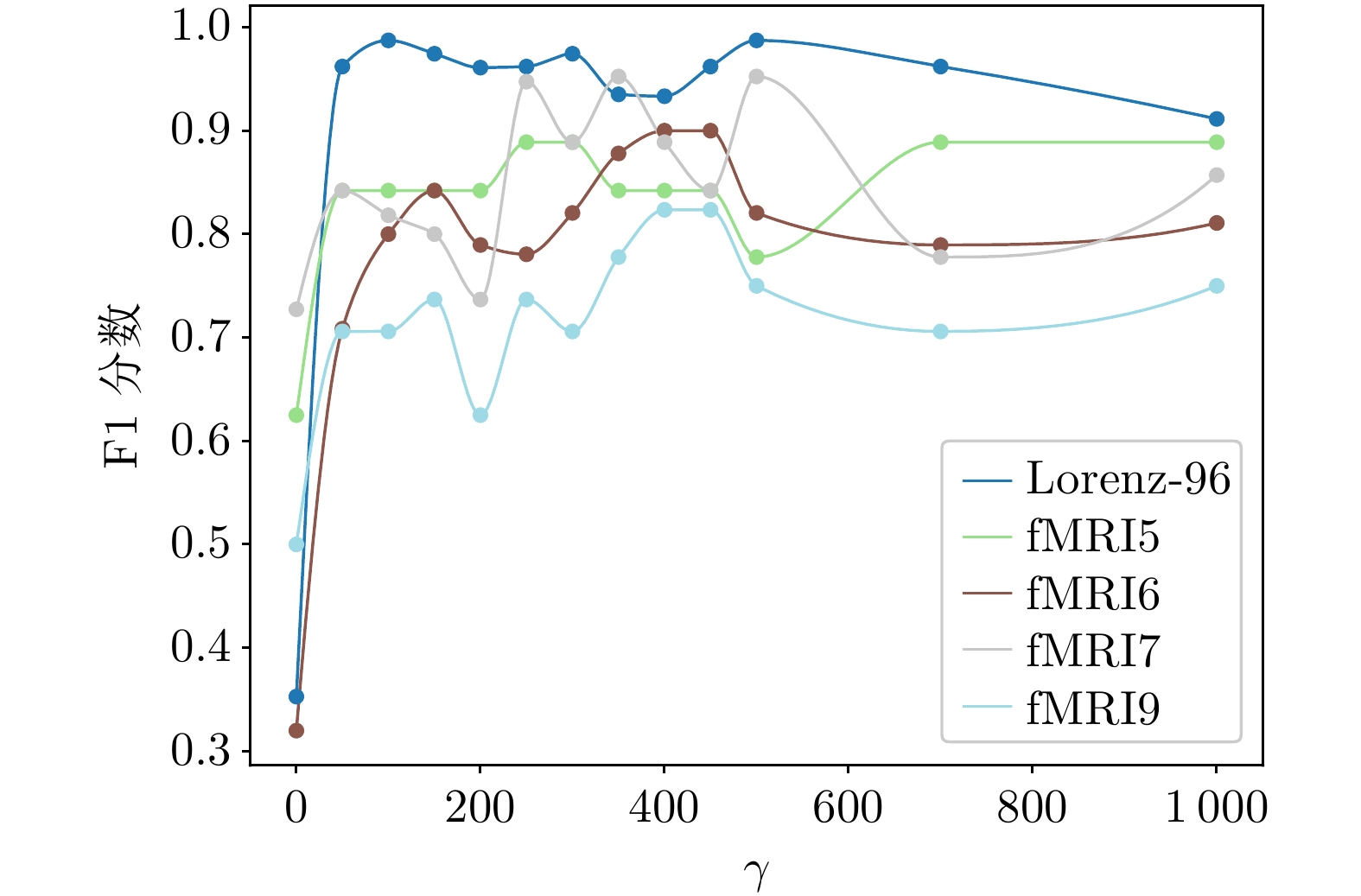
模型	VAR		Lorenz-96		fMRI5		fMRI6		fMRI7		fMRI9
模型	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1
TCDF	96	0.8235	72	0.4528	76	0.6250	86	0.6667	68	0.5000	56	0.4211
PCMCI	96	0.9091	81	0.6250	60	0.6667	82	0.7000	80	0.8000	56	0.6452
eSRU	90	0.7222	83	0.7792	72	0.6316	88	0.6250	68	0.5556	68	0.6363
NGC	98	0.9523	97	0.9630	84	0.7500	92	0.8000	84	0.7500	68	0.5000
GVAR	99	0.9756	98	0.9756	76	0.7692	90	0.6875	88	0.8235	80	0.8059
CRVAE	91	0.8000	96	0.9478	80	0.7619	94	0.8500	80	0.7619	72	0.6923
KTFCDN	100	1.0000	99	0.9873	92	0.8889	96	0.9000	96	0.9524	88	0.8235
注: 加粗字体表示最优结果.

下载: 导出CSV

表 2 时延发现比较实验

Table 2 Time delay discovery comparison experiment

模型	VAR-10	VAR-50	VAR-70	VAR-100	fMRI5	fMRI6	fMRI7	fMRI9
TCDF	1.000	0.9861	0.9327	0.8894	0.8609	0.8805	0.8925	0.9063
PCMCI	1.000	0.9856	0.9830	0.9466	0.8795	0.8962	0.9063	0.9160
NGC	1.000	0.9855	0.9760	0.9020	0.8610	0.8689	0.8570	0.9310
KTFCDN	1.000	1.0000	1.0000	1.0000	0.8972	0.9439	0.9695	0.9975

下载: 导出CSV

表 3 KTFCDN消融研究结果

Table 3 Ablation study results of KTFCDN

模型	VAR		Lorenz-96		fMRI5		fMRI6		fMRI7		fMRI9
模型	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1	Acc (%)	F1
cLSTM	98	0.95	97	0.96	84	0.75	92	0.80	84	0.75	68	0.50
TFCDN	100	1.00	98	0.95	84	0.75	94	0.84	88	0.82	80	0.71
KCDN	100	1.00	94	0.93	88	0.84	94	0.86	92	0.89	84	0.75
KTFCDN	100	1.00	99	0.99	92	0.89	96	0.90	96	0.95	88	0.82

下载: 导出CSV

表 4 KTFCDN运行效率分析

Table 4 Operational efficiency analysis of KTFCDN

节点数量	时间窗口长度	参数量(M)	FLOPs (MMac)	每epoch训练时间(s)
5	10	0.26	2.49	2.37
5	50	0.83	14.85	7.09
5	100	2.54	35.72	9.21
10	10	0.59	5.82	12.26
10	50	1.63	39.23	38.34
10	100	4.77	103.23	93.73
15	10	0.91	9.36	29.66
15	50	2.34	67.26	114.68
15	100	6.62	185.99	280.53

下载: 导出CSV

表 5 聚酯纤维酯化数据集预测实验结果

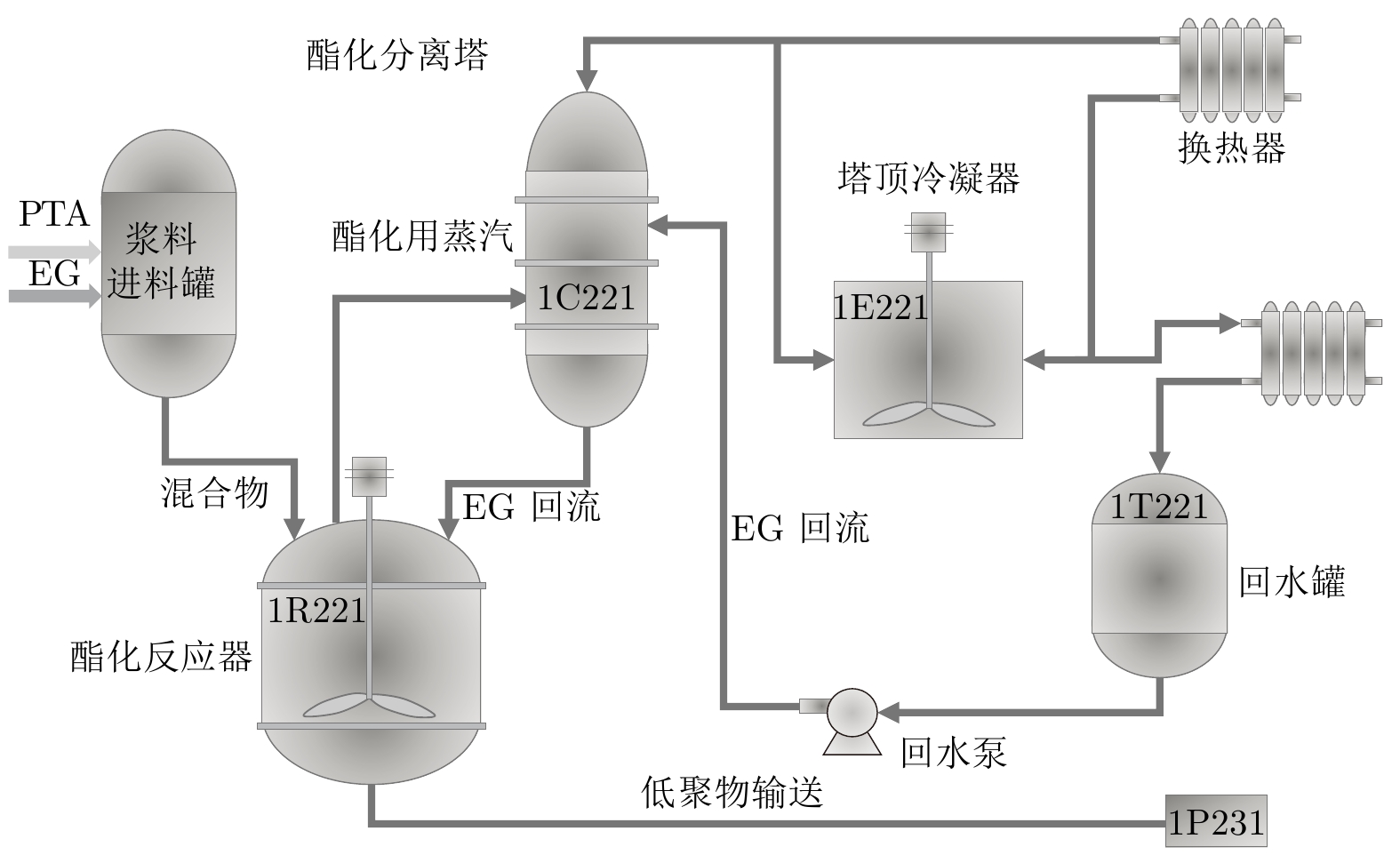
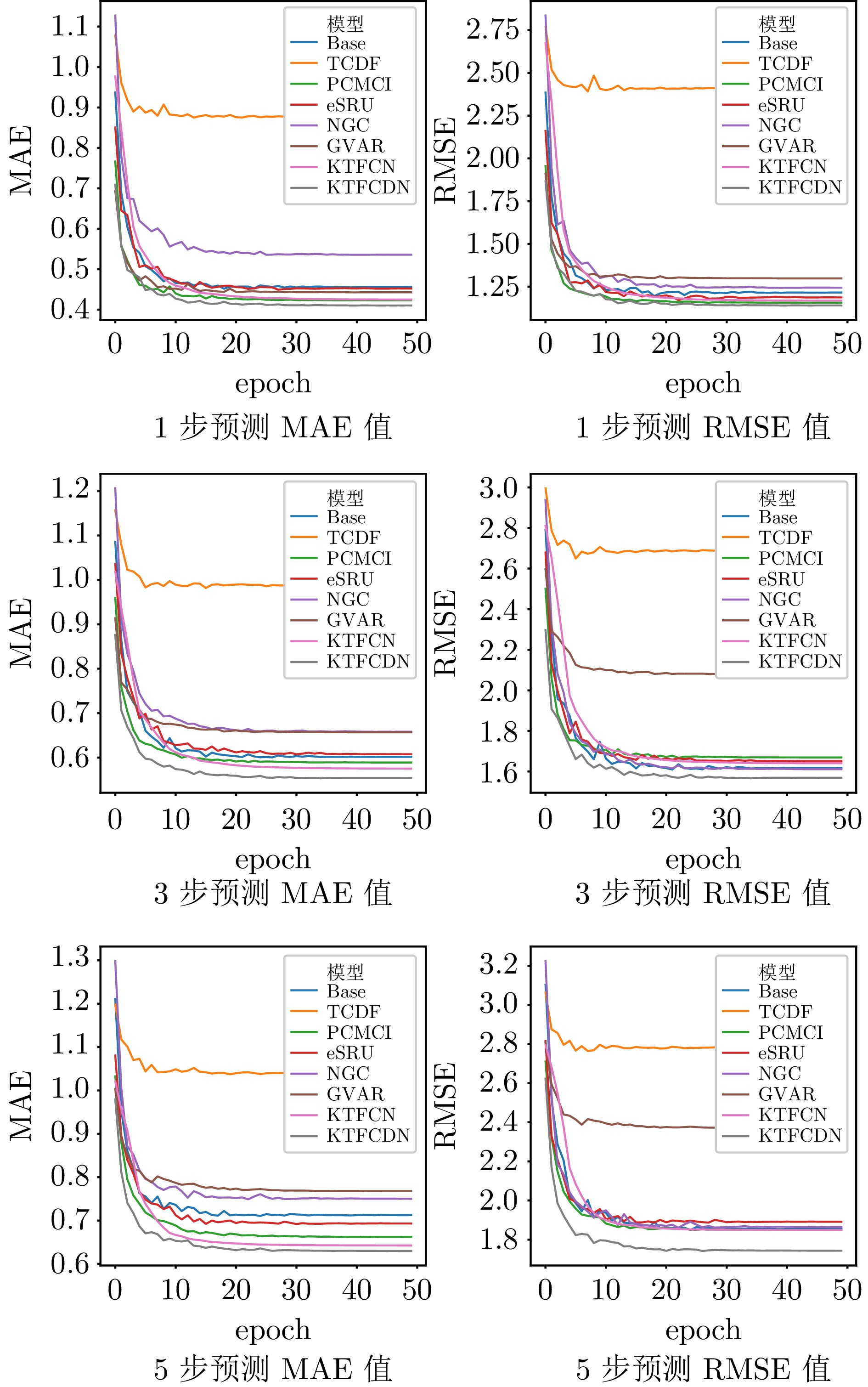
Table 5 Prediction experiment results on the polyester fiber esterification dataset

模型	1步预测		3步预测		5步预测
模型	MAE	RMSE	MAE	RMSE	MAE	RMSE
Base	0.4557	1.2153	0.6016	1.6172	0.7118	1.8534
TCDF	0.8770	2.4114	0.9875	2.6900	1.0401	2.7822
PCMCI	0.4230	1.1564	0.5887	1.6691	0.6623	1.8487
eSRU	0.4520	1.1873	0.6075	1.6512	0.6932	1.8914
GVAR	0.4429	1.2987	0.6568	2.0803	0.7680	2.3720
NGC	0.5360	1.2447	0.6580	1.6117	0.7503	1.8641
KTFCN	0.4250	1.1681	0.5751	1.6408	0.6425	1.8496
KTFCDN	0.4103	1.1403	0.5538	1.5691	0.6298	1.7433

下载: 导出CSV

参考文献(37)

[1]	赵健程, 赵春晖. 面向全量测点耦合结构分析与估计的工业过程监测方法. 自动化学报, 2024, 50(8): 1517−1538 Zhao Jian-Cheng, Zhao Chun-Hui. An industrial process monitoring method based on total measurement point coupling structure analysis and estimation. Acta Automatica Sinica, 2024, 50(8): 1517−1538
[2]	刘雨蒙, 郑旭, 田玲, 王宏安. 基于时序图推理的设备剩余使用寿命预测. 自动化学报, 2024, 50(1): 76−88 Liu Yu-Meng, Zheng Xu, Tian Ling, Wang Hong-An. Remaining useful life estimation of facilities based on reasoning over temporal graphs. Acta Automatica Sinica, 2024, 50(1): 76−88
[3]	唐鹏, 彭开香, 董洁. 一种新颖的深度因果图建模及其故障诊断方法. 自动化学报, 2022, 48(6): 1616−1624 Tang Peng, Peng Kai-Xiang, Dong Jie. A novel method for deep causality graph modeling and fault diagnosis. Acta Automatica Sinica, 2022, 48(6): 1616−1624
[4]	谭帅, 王一帆, 姜庆超, 侍洪波, 宋冰. 基于不同故障传播路径差异化的故障诊断方法. 自动化学报, 2025, 51(1): 161−173 Tan Shuai, Wang Yi-Fan, Jiang Qing-Chao, Shi Hong-Bo, Song Bing. Fault propagation path-aware network: A fault diagnosis method. Acta Automatica Sinica, 2025, 51(1): 161−173
[5]	任伟杰, 韩敏. 多元时间序列因果关系分析研究综述. 自动化学报, 2021, 47(1): 64−78 Ren Wei-Jie, Han Min. Survey on causality analysis of multivariate time series. Acta Automatica Sinica, 2021, 47(1): 64−78
[6]	孙悦雯, 柳文章, 孙长银. 基于因果建模的强化学习控制: 现状及展望. 自动化学报, 2023, 49(3): 661−677 Sun Yue-Wen, Liu Wen-Zhang, Sun Chang-Yin. Causality in reinforcement learning control: The state of the art and prospects. Acta Automatica Sinica, 2023, 49(3): 661−677
[7]	Spirtes P, Glymour C. An algorithm for fast recovery of sparse causal graphs. Social Science Computer Review, 1991, 9(1): 62−72 doi: 10.1177/089443939100900106
[8]	Malinsky D, Spirtes P. Causal structure learning from multivariate time series in settings with unmeasured confounding. In: Proceedings of the ACM SIGKDD Workshop on Causal Discovery. PMLR, 2018. 23−47
[9]	Runge J, Nowack P, Kretschmer M, Flaxman S, Sejdinovic D. Detecting and quantifying causal associations in large nonlinear time series datasets. Science Advances, 2019, 5(11): Article No. eaau4996 doi: 10.1126/sciadv.aau4996
[10]	Runge J. Discovering contemporaneous and lagged causal relations in autocorrelated nonlinear time series datasets. In: Proceedings of the 36th Conference on Uncertainty in Artificial Intelligence (UAI). PMLR, 2020. 1388−1397
[11]	Assaad C K, Devijver E, Gaussier E. Discovery of extended summary graphs in time series. In: Proceedings of the 38th Conference on Uncertainty in Artificial Intelligence. Eindhoven, The Netherlands: PMLR, 2022. 96−106
[12]	Shimizu S, Hoyer P O, Hyvärinen A, Kerminen A. A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 2006, 7: 2003−2030
[13]	Hyvärinen A, Shimizu S, Hoyer P O. Causal modelling combining instantaneous and lagged effects: An identifiable model based on non-Gaussianity. In: Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland: Association for Computing Machinery, 2008. 424−431
[14]	Hyvärinen A, Zhang K, Shimizu S, Hoyer P O. Estimation of a structural vector autoregression model using non-Gaussianity. Journal of Machine Learning Research, 2010, 11: 1709−1731
[15]	Zheng X, Aragam B, Ravikumar P, Xing E P. DAGs with no TEARS: Continuous optimization for structure learning. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc., 2018. 9492−9503
[16]	Pamfil R, Sriwattanaworachai N, Desai S, Pilgerstorfer P, Beaumont P, Georgatzis K, et al. DYNOTEARS: Structure learning from time-series data. In: Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS). Palermo, Italy: PMLR, 2020. 1595−1605
[17]	Sun X Y, Schulte O, Liu G L, Poupart P. NTS-NOTEARS: Learning nonparametric DBNs with prior knowledge. In: Proceedings of the 26th International Conference on Artificial Intelligence and Statistics. Valencia, Spain: PMLR, 2023. 1942−1964
[18]	Kaiser M, Sipos M. Unsuitability of NOTEARS for causal graph discovery when dealing with dimensional quantities. Neural Processing Letters, 2022, 54(3): 1587−1595 doi: 10.1007/s11063-021-10694-5
[19]	Granger C W J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 1969, 37(3): 424−438 doi: 10.2307/1912791
[20]	Nauta M, Bucur D, Seifert C. Causal discovery with attention-based convolutional neural networks. Machine Learning and Knowledge Extraction, 2019, 1(1): 312−340
[21]	Liang X X, Hao K R, Chen L, Cai X, Hao L G. Causal inference of multivariate time series in complex industrial systems. Advanced Engineering Informatics, 2024, 59: Article No. 102320 doi: 10.1016/j.aei.2023.102320
[22]	Tank A, Covert I, Foti N, Shojaie A, Fox E B. Neural granger causality. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 44(8): 4267−4279
[23]	Marinazzo D, Pellicoro M, Stramaglia S. Kernel method for nonlinear Granger causality. Physical Review Letters, 2008, 100(14): Article No. 144103 doi: 10.1103/PhysRevLett.100.144103
[24]	Ren W J, Li B S, Han M. A novel Granger causality method based on HSIC-Lasso for revealing nonlinear relationship between multivariate time series. Physica A: Statistical Mechanics and Its Applications, 2020, 541: Article No. 123245 doi: 10.1016/j.physa.2019.123245
[25]	Gu A, Dao T, Ermon S, Rudra A, Ré C. HiPPO: Recurrent memory with optimal polynomial projections. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc., 2020. Article No. 125
[26]	Gu A, Gupta A, Goel K, Ré C. On the parameterization and initialization of diagonal state space models. In: Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans, USA: Curran Associates Inc., 2022. Article No. 2607
[27]	Gu A, Dao T. Mamba: Linear-time sequence modeling with selective state spaces. In: Proceedings of the 1st Conference on Language Modeling. Philadelphia, USA: OpenReview.net, 2023.
[28]	张宪法, 郝矿荣, 陈磊. 免疫多域特征融合的多核学习SVM运动想象脑电信号分类. 自动化学报, 2020, 46(11): 2417−2426 Zhang Xian-Fa, Hao Kuang-Rong, Chen Lei. Motor imagery EEG classification based on immune multi-domain-feature fusion and multiple kernel learning SVM. Acta Automatica Sinica, 2020, 46(11): 2417−2426
[29]	Korda M, Mezić I. Optimal construction of Koopman eigenfunctions for prediction and control. IEEE Transactions on Automatic Control, 2020, 65(12): 5114−5129 doi: 10.1109/TAC.2020.2978039
[30]	Bevanda P, Beier M, Lederer A, Lederer S, Hüllermeier E, Hirche S. Koopman kernel regression. In: Proceedings of the 37th International Conference on Neural Information Processing Systems. New Orleans, USA: Curran Associates Inc., 2024. Article No. 713
[31]	Micchelli C A, Pontil M. On learning vector-valued functions. Neural Computation, 2005, 17(1): 177−204 doi: 10.1162/0899766052530802
[32]	Karimi A, Paul M R. Extensive chaos in the Lorenz-96 model. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2010, 20(4): Article No. 043105 doi: 10.1063/1.3496397
[33]	Smith S M, Miller K L, Salimi-Khorshidi G, Webster M, Beckmann C F, Nichols T E, et al. Network modelling methods for fMRI. Neuroimage, 2011, 54(2): 875−891 doi: 10.1016/j.neuroimage.2010.08.063
[34]	Khanna S, Tan V Y F. Economy statistical recurrent units for inferring nonlinear Granger causality. In: Proceedings of the 8th International Conference on Learning Representations. Addis Ababa, Ethiopia: OpenReview.net, 2020.
[35]	Marcinkevičs R, Vogt J E. Interpretable models for Granger causality using self-explaining neural networks. In: Proceedings of the International Conference on Learning Representations. Vienna, Austria: OpenReview.net, 2021.
[36]	Li H M, Yu S J, Principe J. Causal recurrent variational autoencoder for medical time series generation. In: Proceedings of the 37th AAAI Conference on Artificial Intelligence. Washington, USA: AAAI Press, 2023. Article No. 962
[37]	Ding H, Hao K R, Chen L, Shi X. Feature structured domain adaptation for quality prediction of cross working conditions in industrial processes. Journal of Manufacturing Systems, 2024, 74: 887−900 doi: 10.1016/j.jmsy.2024.05.011