Two-population Co-evolutionary Algorithm for Constrained Multi-objective Optimization Problems in Complex Feasible Domains
-
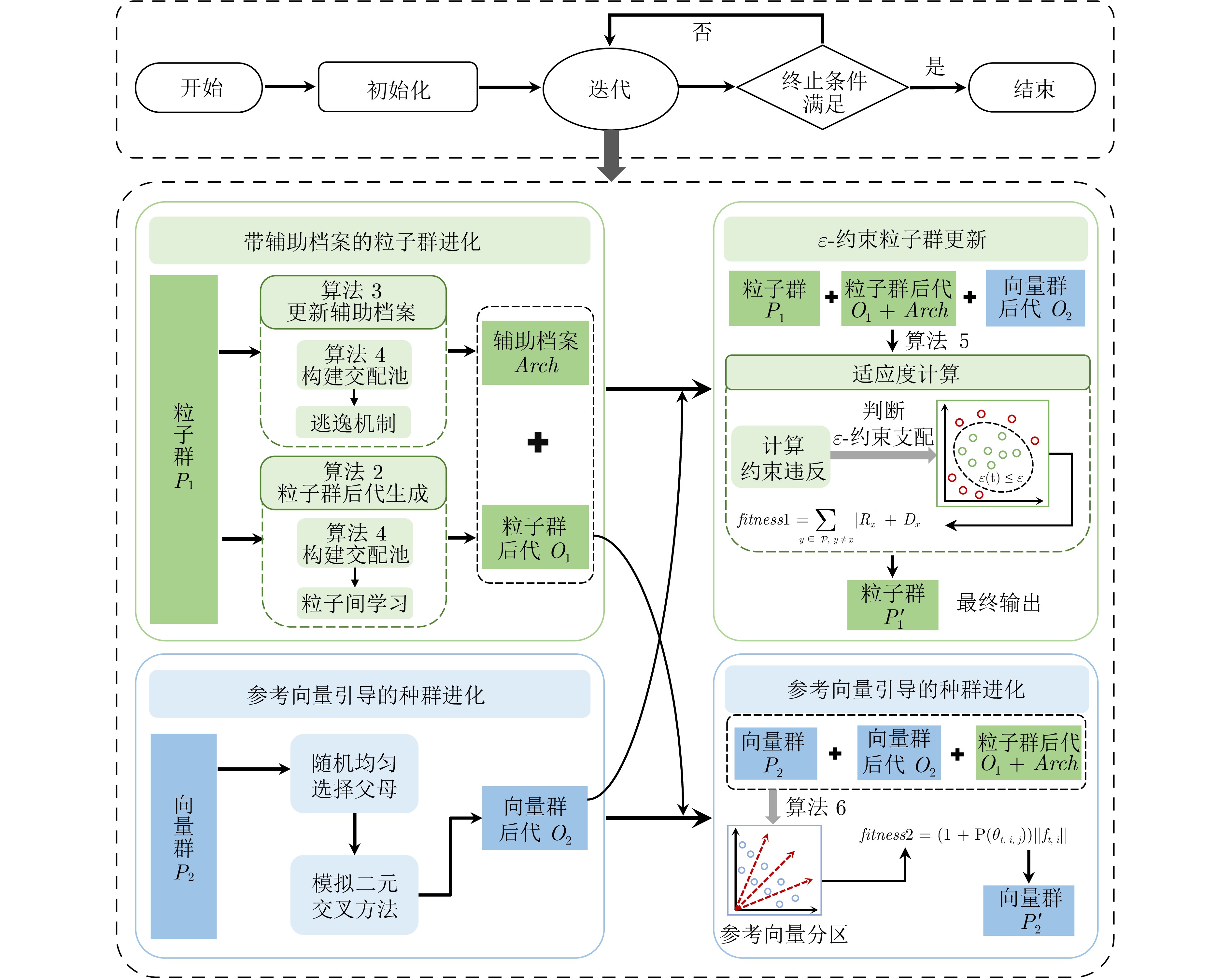
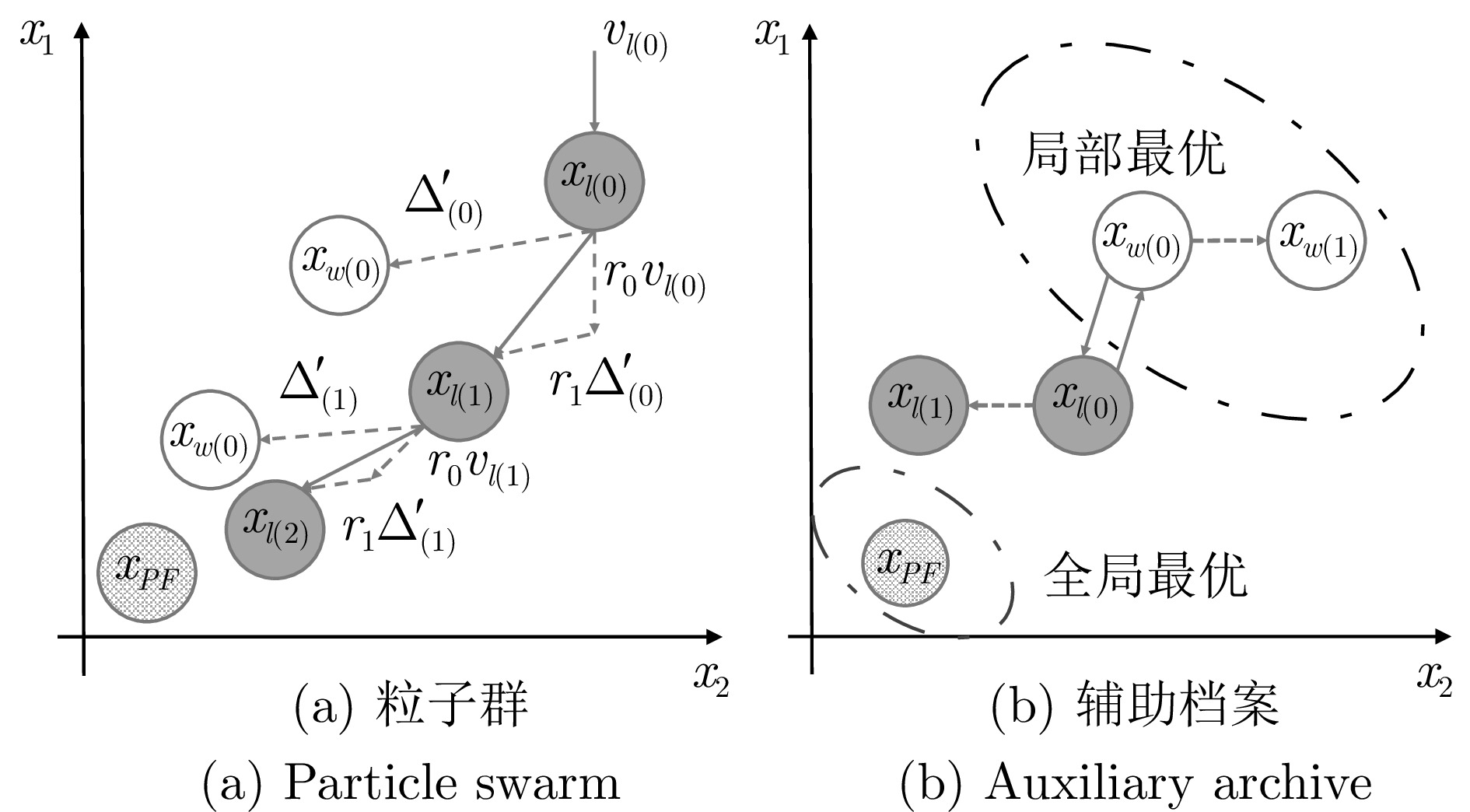
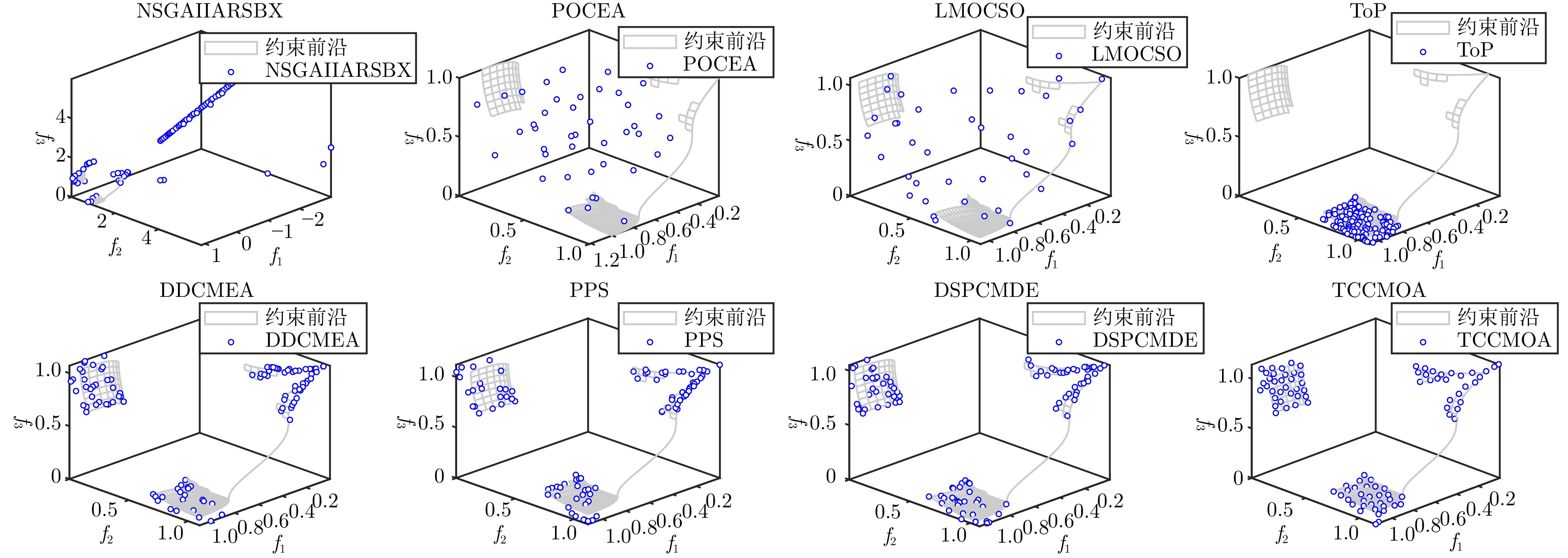
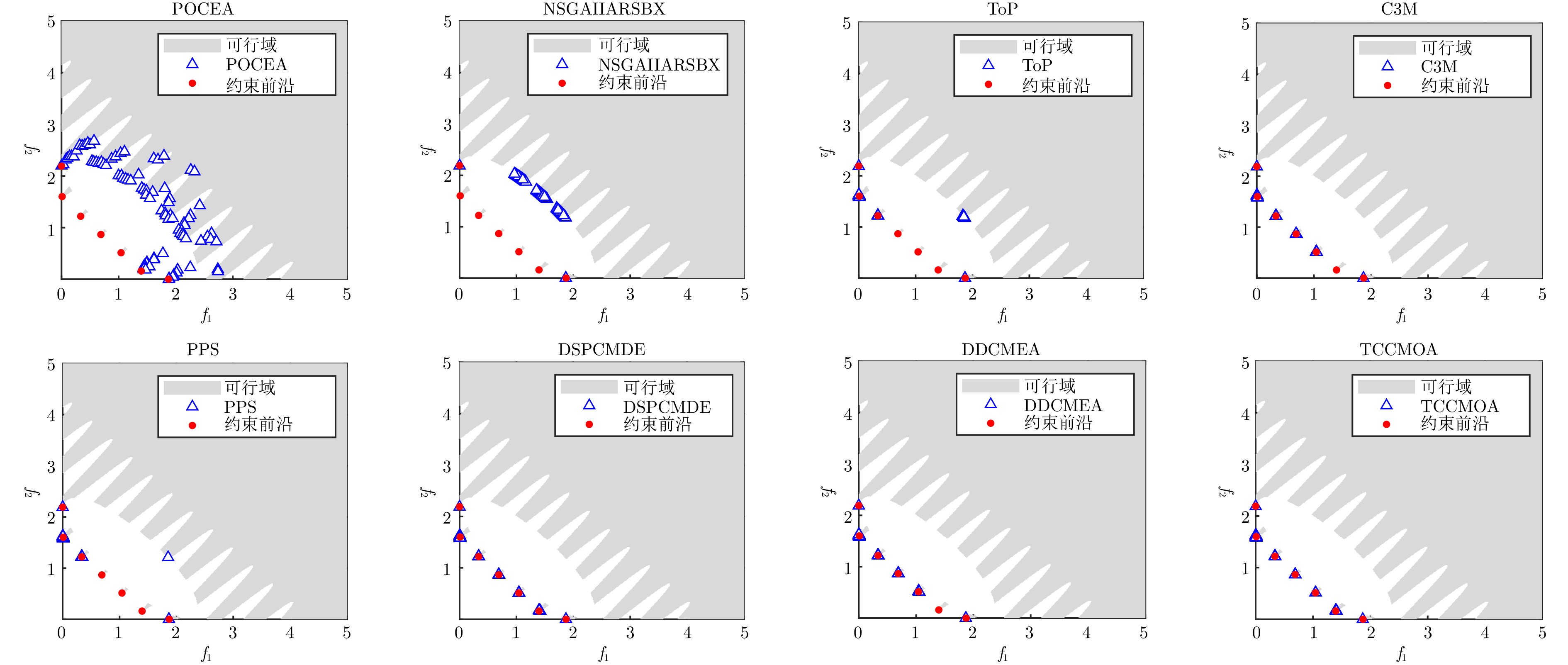
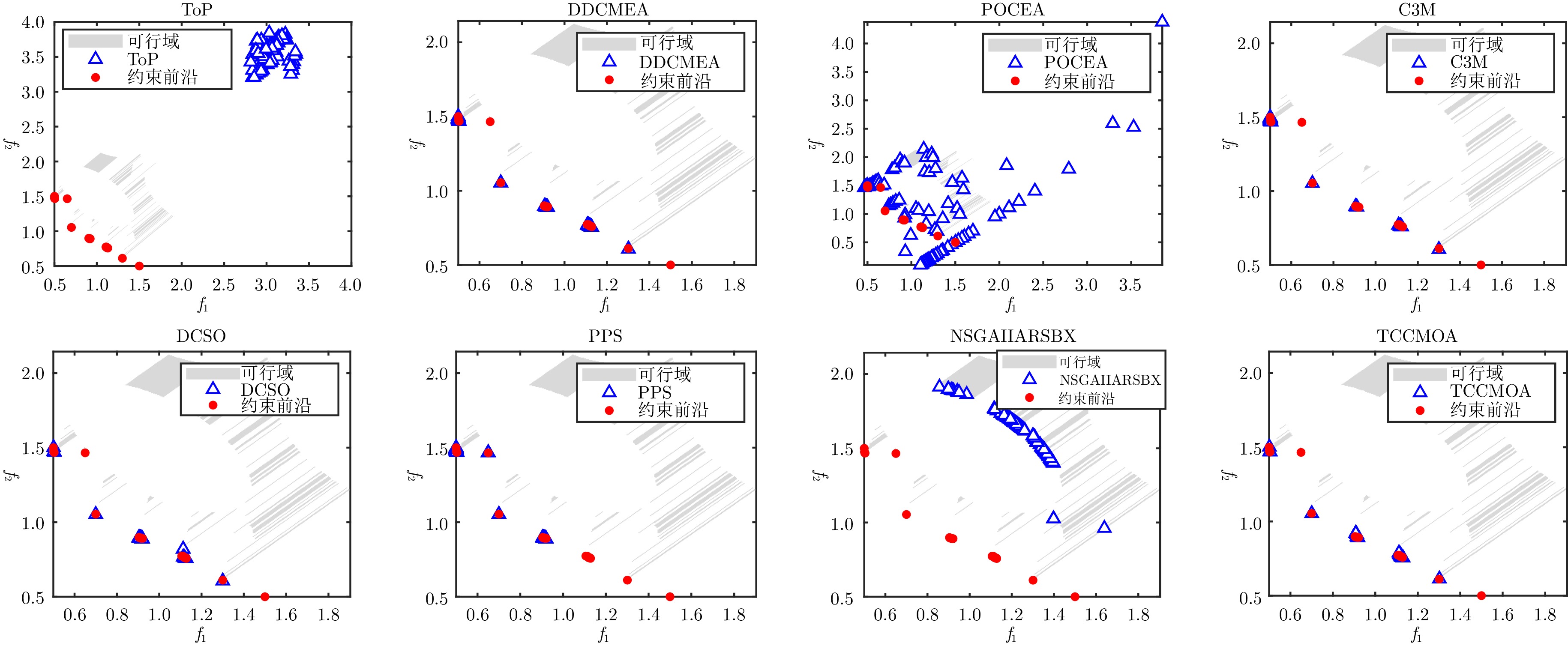
摘要: 约束多目标优化问题主要考虑如何在复杂约束条件下同时优化多个相互冲突的目标, 其广泛存在于工程实践中. 解决约束多目标优化问题的关键在于约束满足和目标优化之间的平衡. 然而, 当问题具有复杂可行域时, 现有算法往往存在着选择压力大小的矛盾: 若算法的选择压力较大, 种群容易陷入局部最优; 若算法的选择压力较小, 种群则难以搜索到完整的约束前沿. 针对此, 提出一种面向复杂约束的双种群协同进化多目标优化算法. 所提算法采用双种群协同进化框架, 引入粒子群和向量群以实现种群间的信息共享和优势互补. 其中粒子群使用带有辅助档案的粒子群优化器, 通过粒子间的相互学习实现快速收敛, 而辅助档案则借助逃逸机制帮助粒子群跳出局部最优. 同时, 设计一种新的$\epsilon$-约束技术, 动态调整约束松弛因子, 使种群在进化初期注重不可行解的遗传信息, 跨越不可行区域. 向量群使用不考虑约束的参考向量法引导种群进化, 使得种群均匀分布于前沿面, 有效维护了种群的多样性. 在当前基准测试集和真实世界71个问题上的实验结果表明, 所提出的算法超越对比算法, 能够在保持种群多样性的同时快速收敛到约束前沿.Abstract: Constrained multi-objective optimization problems mainly consider simultaneously optimizing multiple conflicting objectives under complex constraint conditions, which are widely used in engineering practice. The key to solving multi-objective optimization problems lies in balancing constraint satisfaction with objective optimization. However, when tackling problems with complex feasible domains, existing algorithms often face a trade-off in selection pressure: Excessive pressure may lead to population convergence to local optima, while insufficient pressure can hinder the discovery of the complete constraint front. To address the above issues, this paper proposes a two-population co-evolutionary constrained multi-objective optimization algorithm (TCCMOA). The proposed algorithm adopts a two-population co-evolutionary framework and introduces particle swarm and vector swarm to achieve information sharing and complementary advantages between populations. The particle swarm uses a particle swarm optimizer with auxiliary files to achieve fast convergence through mutual learning between particles, while the auxiliary files help the particle swarm escape from local optima through escape mechanisms. Meanwhile, a new$\epsilon$-constraint technology is designed to dynamically adjust the constraint relaxation factor, so that the population pays attention to the infeasible genetic information in the early stage of evolution and crosses the infeasible domains. Vector swarm employs the unconstrained reference vector method to guide population evolution, resulting in a uniform distribution of the population on the frontier and effectively maintaining population diversity. The experimental results on 71 problems in benchmark and real-world sets show that TCCMOA outperforms the comparative algorithms and is able to quickly converge to the constrained frontier while maintaining the diversity of the population.
-
图 1 CMOEA解决约束多目标优化问题的两类典型场景
Fig. 1 Two typical scenarios for CMOEA to solve constrained multi-objective optimization problems
图 4 各算法在DC2-DTLZ3问题上的种群分布
Fig. 4 Population distribution of each algorithm on the DC2-DTLZ3 problem
图 5 各算法在ZXH-CF问题上的收敛曲线
Fig. 5 Convergence curve of each algorithm on the ZXH-CF problem
图 6 各算法在ZXH-CF9问题上的种群分布
Fig. 6 Population distribution of each algorithm on the ZXH-CF9 problem
图 7 各算法在LIRCMOP问题上的收敛曲线
Fig. 7 Convergence curve of each algorithm on the LIRCMOP problem
图 8 各算法在LIR-CMOP11问题上的种群分布
Fig. 8 Population distribution of each algorithm on the LIR-CMOP11 problem
图 9 各算法在DAS-CMOP6问题上的种群分布
Fig. 9 Population distribution of each algorithm on the DAS-CMOP6 problem
图 11 各算法在MW5问题上的种群分布
Fig. 11 Population distribution of each algorithm on the MW5 problem
图 12 由TCCMOA及其变体在测试问题上获得的IGD+ 值
Fig. 12 IGD+ values obtained by TCCMOA and its variants on test problems
图 13 各算法在LIRCMOP7、LIRCMOP8、MW7和MW11问题上的收敛曲线
Fig. 13 Convergence curves of each algorithm on LIRCMOP7、LIRCMOP8、MW7 and MW11 problems
表 1 各测试问题的难度特征
Table 1 Difficulty characteristics of each test question
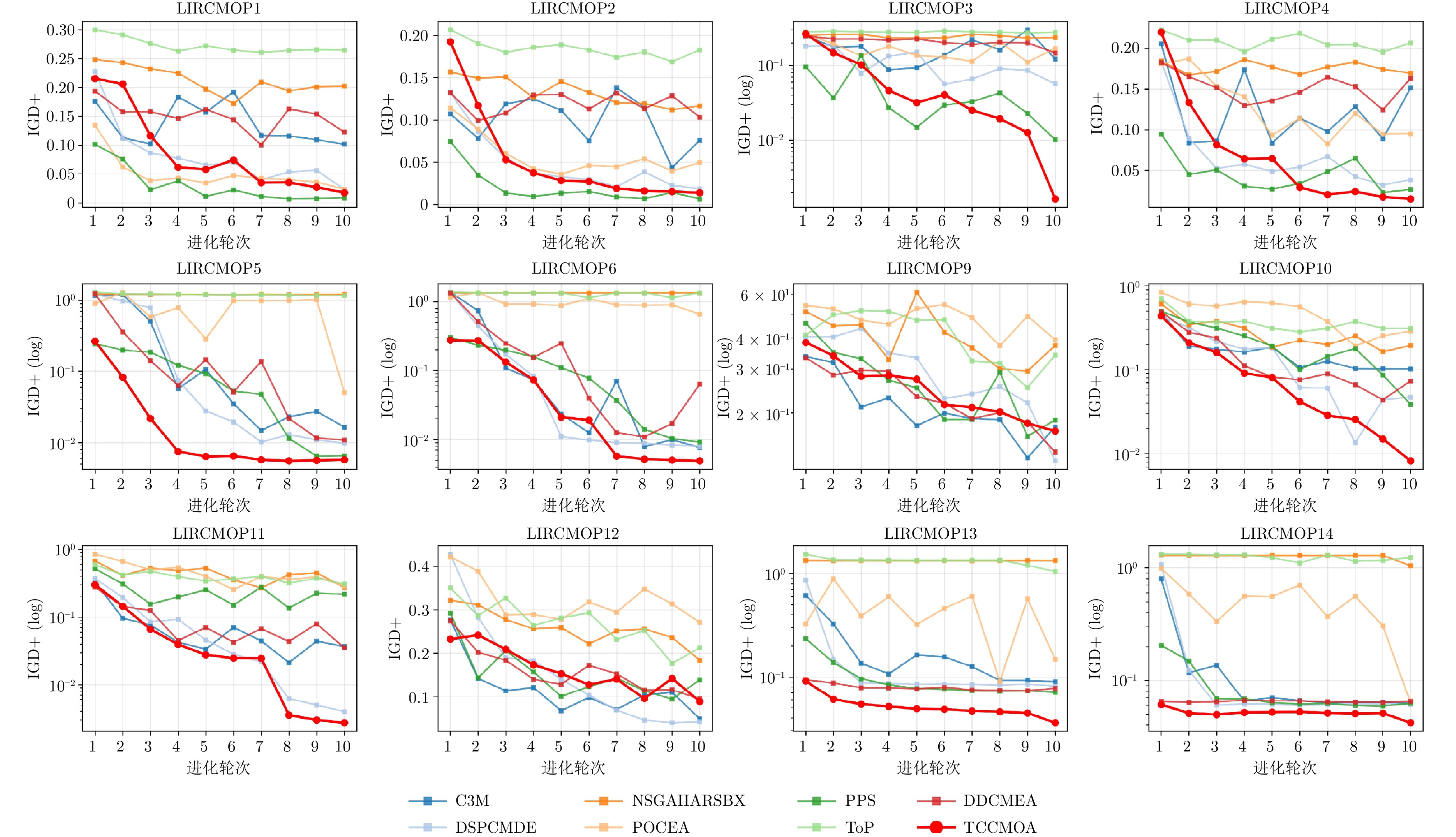
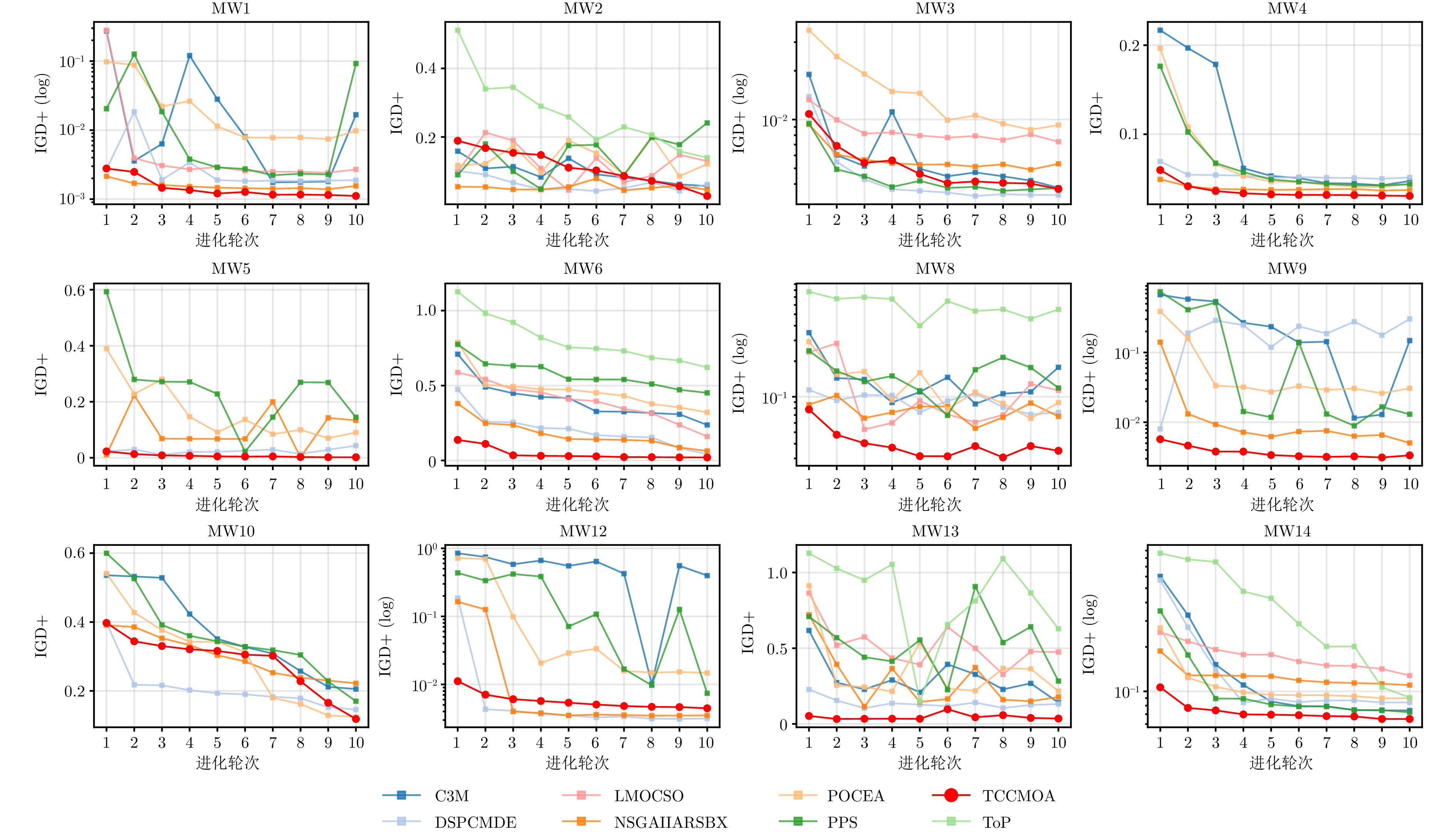
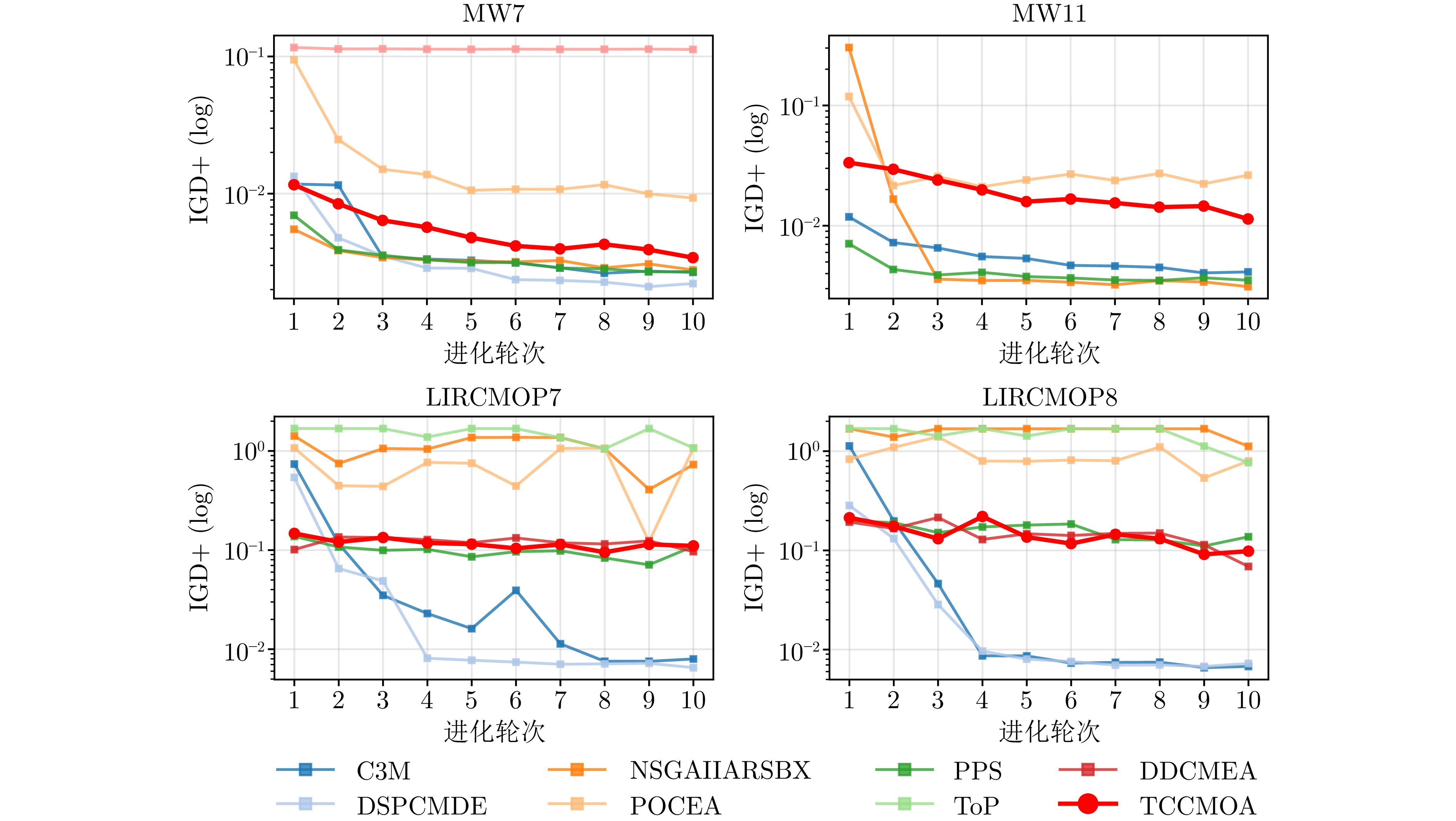
问题类型 问题集名 问题名 目标数 问题特征 基准问题 DTLZ[39] C1-DTLZ1、C1-DTLZ3、DC2-DTLZ1、DC2-DTLZ3 3 可行域连续、平面 DC2-DTLZ1、DC3-DTLZ1、DC3-DTLZ1 3 可行域不连续、平面 C2-DTLZ2、DC1-DTLZ3、DC3-DTLZ3 3 可行域不连续、凸面/凹面 ZXH-CF[40] ZXH-CF1 ~ ZXH-CF9 3 可行域连续、不规则凸面/凹面 ZXH-CF10 ~ ZXH-CF12 3 可行域较离散、凸面 ZXH-CF13 ~ ZXH-CF16 2 可行域不连续 LIR-CMOP[41] LIR-CMOP1 ~ LIR-CMOP4 2 可行域为线条、高度离散 LIR-CMOP5 ~ LIR-CMOP12 2 可行域不规则、跨度大、高度离散 LIR-CMOP13 ~ LIR-CMOP14 3 可行域连续、凸面 DAS-CMOP[42] DAS-CMOP1 ~ DAS-CMOP2 2 可行域不规则、跨度大 DAS-CMOP3 ~ DAS-CMOP6 2 可行域面积小、跨度大、高度离散 DAS-CMOP7 ~ DAS-CMOP9 3 可行域离散 MW[43] MW1 ~ MW7 2 可行域面积小、跨度大 MW8 ~ MW10 3 可行域不连续 MW11 ~ MW14 3 可行域高度离散 真实问题 RWMOP[38] RWMOP7、RWMOP9、RWMOP18 3 工艺设计和合成问题 RWMOP8、RWMOP11、RWMOP17 3、5 交通分配问题 RWMOP21、RWMOP23、RWMOP28、RWMOP50 2 工业实践问题 
下载: 导出CSV
表 2 各算法在DTLZ问题的IGD+ 和HV值
Table 2 IGD+ and HV value of each algorithm on DTLZ problem
测试问题 $M$ $D$ 评估指标 C3M DSPCMDE LMOCSO NSGAIIARSBX PPS ToP DDCMEA TCCMOA C1-DTLZ1 3 7 IGD+ 1.7509e−2
(4.55e−4) −2.1804e−2
(8.07e−4) −1.6772e−2
(9.39e−4) −1.7833e−2
(5.74e−4) −1.8637e−2
(6.10e−4) −2.6791e−1
(0.00e+0) =1.9936e−2
(8.96e−4) −1.4899e−2
(1.41e−4)HV 8.2479e−1
(3.01e−3) −8.1413e−1
(3.88e−3) −8.2411e−1
(6.22e−3) −8.2414e−1
(4.74e−3) −8.1887e−1
(4.14e−3) −2.0265e−1
(0.00e+0) =8.1663e−1
(4.27e−3) −8.3958e−1
(7.68e−4)C1-DTLZ3 3 12 IGD+ 5.7411e−1
(1.46e+0) −5.1905e−1
(3.10e−1) −2.4319e+0
(2.65e+0) −8.0242e+0
(3.50e−3) −2.4378e+0
(3.72e+0) −6.4953e−1
(2.02e+0) −7.5252e−2
(6.73e−2) −3.9000e−2
(4.31e−2)HV 3.1257e−1
(2.30e−1) −8.5935e−2
(1.22e−1) −6.9245e−3
(3.51e−2) −0.0000e+0
(0.00e+0) −3.5977e−1
(2.40e−1) −3.9272e−1
(1.76e−1) −4.6661e−1
(1.03e−1) −5.3301e−1
(7.01e−2)C2-DTLZ2 3 12 IGD+ 3.0515e−2
(1.26e−3) −2.9212e−2
(1.21e−3) −2.0933e−2
(5.59e−5) −2.5483e−2
(1.57e−3) −2.4649e−2
(8.15e−4) −3.7790e−2
(9.99e−3) −2.9711e−2
(9.61e−4) −1.9637e−2
(5.23e−4)HV 4.9210e−1
(3.19e−3) −4.8276e−1
(4.74e−3) −5.1353e−1
(1.10e−4) −4.8684e−1
(5.78e−3) −4.9930e−1
(3.07e−3) −4.6411e−1
(2.20e−2) −4.8491e−1
(4.02e−3) −5.1512e−1
(1.30e−3)C3-DTLZ4 3 12 IGD+ 7.5829e−2
(3.37e−3) −8.6626e−2
(4.89e−3) −1.3588e+0
(2.59e−1) −9.1908e−2
(6.47e−3) −9.1537e−2
(3.29e−2) −1.0547e−1
(6.46e−3) −1.0289e−1
(6.91e−3) −6.9539e−2
(3.13e−3)HV 7.7709e−1
(2.31e−3) −7.6844e−1
(3.69e−3) −5.9995e−2
(8.38e−2) −7.6295e−1
(4.50e−3) −7.6019e−1
(2.79e−2) −7.5560e−1
(4.82e−3) −7.5770e−1
(3.62e−3) −7.8085e−1
(2.06e−3)DC1-DTLZ1 3 7 IGD+ 2.6581e−2
(4.64e−2) −3.0582e−1
(3.95e−1) −1.9135e−2
(2.68e−3) −9.9365e−3
(5.11e−4) −1.9375e−2
(5.51e−3) −1.8548e−2
(4.14e−3) −1.3418e−2
(6.75e−4) −8.9133e−3
(4.10e−4)HV 5.7172e−1
(7.71e−2) −2.4009e−1
(2.71e−1) −5.7778e−1
(1.23e−2) −6.1418e−1
(3.74e−3) −5.7806e−1
(2.70e−2) −5.7923e−1
(2.47e−2) −6.0775e−1
(3.42e−3) −6.2870e−1
(1.62e−3)DC1-DTLZ3 3 12 IGD+ 9.6777e−1
(9.42e−1) −4.1637e−1
(3.02e−1) −1.4113e+0
(9.35e−1) −2.5727e−2
(2.91e−2) =2.0563e−1
(1.81e−1) −1.1143e+0
(1.82e+0) −2.8828e−2
(2.90e−2) =3.9102e−2
(5.21e−2)HV 9.9370e−2
(1.52e−1) −8.9387e−2
(9.92e−2) −2.1911e−4
(9.25e−4) −4.4500e−1
(5.42e−2) =3.0973e−1
(1.27e−1) −1.5810e−1
(1.75e−1) −4.3930e−1
(5.24e−2) +4.2518e−1
(9.04e−2)DC2-DTLZ1 3 7 IGD+ 2.1651e−2
(9.50e−4) −2.5152e−2
(8.33e−4) −4.5109e−2
(9.46e−2) −NaN
(NaN)2.1542e−2
(1.09e−3) −NaN
(NaN)2.1560e−2
(9.93e−4) −1.5149e−2
(1.99e−4)HV 8.2594e−1
(2.15e−3) −8.1577e−1
(2.27e−3) −7.7358e−1
(2.06e−1) −NaN
(NaN)8.0975e−1
(5.18e−3) −NaN
(NaN)8.2251e−1
(2.28e−3) −8.4013e−1
(4.52e−4)DC2-DTLZ3 3 12 IGD+ 3.8084e−1
(2.52e−1) −5.3330e−1
(1.59e−1) −7.9948e−1
(7.45e−2) −5.6957e−1
(0.00e+0) =3.6856e−1
(2.61e−1) −NaN
(NaN)4.7017e−1
(2.26e−1) −4.3270e−2
(3.28e−2)HV 1.9504e−1
(2.42e−1) −5.3927e−2
(1.38e−1) −1.1416e−3
(1.05e−3) −1.0912e−2
(0.00e+0) =2.0265e−1
(2.48e−1) −NaN
(NaN)1.1604e−1
(2.17e−1) −5.2582e−1
(5.41e−2)DC3-DTLZ1 3 7 IGD+ 8.1686e−1
(6.08e−1) −3.0707e−1
(2.78e−1) −1.9788e−2
(1.24e−2) −1.7092e−1
(1.54e−1) −4.3902e−1
(8.48e−1) −3.2743e+0
(4.48e+0) −8.4586e−3
(3.94e−4) −5.7955e−3
(8.07e−4)HV 6.4447e−2
(1.64e−1) −2.1234e−1
(2.65e−1) −4.6399e−1
(3.39e−2) −2.0666e−1
(2.19e−1) −2.1950e−1
(2.07e−1) −1.9181e−2
(6.68e−2) −5.2439e−1
(2.37e−3) −5.3011e−1
(3.67e−3)DC3-DTLZ3 3 12 IGD+ 2.0297e+0
(1.85e+0) −6.1418e−1
(2.28e−1) −2.2840e+0
(1.18e+0) −2.1112e+0
(5.94e−1) −2.4475e+0
(2.15e+0) −7.7391e+0
(3.47e+0) −6.0506e−1
(2.58e−1) −9.7950e−2
(1.62e−1)HV 4.3100e−2
(1.04e−1) −7.4984e−3
(3.90e−2) −0.0000e+0
(0.00e+0) −0.0000e+0
(0.00e+0) −0.0000e+0
(0.00e+0) −0.0000e+0
(0.00e+0) −2.3808e−2
(9.06e−2) −2.6226e−1
(1.13e−1)+/−/= 0/20/0 0/20/0 0/19/1 1/17/2 0/20/0 0/18/2 1/18/1
下载: 导出CSV
表 3 各算法在DAS-CMOP问题的IGD+和HV值
Table 3 IGD+ and HV value of each algorithm in the DAS-CMOP problem
测试问题 $M$ $D$ 评估指标 C3M DCSO NSGAIIARSBX POCEA PPS ToP DDCMEA TCCMOA DASCMOP1 2 30 IGD+ 2.1124e−3
(2.01e−4) +2.7371e−2
(2.48e−1) −2.0231e−1
(2.90e−1) =3.0176e−2
(5.85e−3) −1.6893e−1
(1.97e−1) =6.8835e−1
(2.05e−1) −4.1346e−1
(3.39e−1) −3.3086e−3
(4.77e−4)HV 2.1197e−1
(6.94e−4) +1.2892e−1
(7.40e−2) −1.5182e−1
(8.68e−2) =1.8749e−1
(5.80e−3) −1.6336e−1
(5.79e−2) −2.3376e−2
(5.10e−2) −9.4062e−2
(9.56e−2) −2.1082e−1
(9.98e−4)DASCMOP2 2 30 IGD+ 3.5343e−3
(1.05e−4) +4.7369e−2
(6.13e−2)+8.8214e−2
(4.47e−2) −3.1520e−2
(4.19e−3) −4.0212e−3
(1.42e−4) +5.3699e−1
(3.20e−1) −1.2465e−1
(2.65e−2) −4.7645e−3
(3.11e−4)HV 3.5497e−1
(9.73e−5) +3.2547e−1
(4.10e−2) =2.9288e−1
(3.22e−2) −3.3423e−1
(3.27e−3) −3.5478e−1
(8.31e−5) +1.1005e−1
(1.15e−1) −2.6924e−1
(1.90e−2) −3.5401e−1
(2.46e−4)DASCMOP3 2 30 IGD+ 4.0398e−2
(4.66e−2) =8.2903e−2
(2.20e−2) −1.8725e−1
(1.26e−2) −7.6793e−2
(6.67e−2) −1.4703e−1
(7.53e−2) −7.1133e−1
(1.08e−1) −1.9098e−1
(7.95e−3) −1.0704e−2
(1.44e−2)HV 2.9554e−1
(2.36e−2) =2.6387e−1
(5.98e−3) −2.1044e−1
(8.24e−3) −2.7256e−1
(3.04e−2) −2.3264e−1
(4.25e−2) −2.9380e−2
(3.53e−2) −2.0885e−1
(1.42e−3) −3.0822e−1
(9.07e−3)DASCMOP4 2 30 IGD+ 6.2087e−2
(2.01e−1) −1.1484e−3
(5.63e−4) +2.3649e−1
(1.23e−1) −9.6946e−2
(1.03e−1) −1.5221e−1
(6.88e−2) −NaN
(NaN)1.5878e−3
(1.00e−3) +6.7979e−3
(1.46e−3)HV 1.8470e−1
(5.26e−2) −2.0357e−1
(5.33e−4) +1.0540e−1
(4.84e−2) −1.5360e−1
(3.19e−2) −1.6916e−1
(1.65e−2) −NaN
(NaN)2.0295e−1
(1.86e−3) +1.9320e−1
(4.15e−3)DASCMOP5 2 30 IGD+ 5.6953e−2
(1.97e−1) −2.9481e−3
(2.38e−4) +2.9456e−1
(1.99e−1) −3.8230e−2
(1.67e−2) −1.5977e−2
(4.26e−2) −NaN
(NaN)3.3727e−3
(7.66e−4) +6.8424e−3
(1.08e−3)HV 3.2660e−1
(8.24e−2) −3.5044e−1
(1.45e−4) +1.7887e−1
(1.13e−1) −3.2540e−1
(9.42e−3) −3.4174e−1
(3.01e−2) −NaN
(NaN)3.5043e−1
(7.16e−4) +3.4702e−1
(8.41e−4)DASCMOP6 2 30 IGD+ 6.8374e−2
(2.16e−1) −1.3818e−2
(1.08e−2) −5.8030e−1
(9.20e−2) −7.4900e−2
(3.75e−2) −2.9387e−1
(3.17e−1) −NaN
(NaN)2.5512e−1
(2.29e−1) =1.1388e−2
(1.77e−3)HV 2.8710e−1
(7.90e−2) =3.0659e−1
(1.13e−2) =4.5735e−2
(1.67e−2) −2.6878e−1
(2.05e−2) −1.8412e−1
(1.33e−1) −NaN
(NaN)1.8346e−1
(1.14e−1) =3.0801e−1
(1.32e−3)DASCMOP7 3 30 IGD+ 5.4260e−2
(1.65e−2) −3.7220e−2
(7.02e−4) −3.7285e−2
(2.77e−3) −6.7471e−2
(2.45e−2) −9.8420e−2
(8.77e−2) −NaN
(NaN)4.9529e−2
(4.15e−3) −3.5298e−2
(2.68e−3)HV 2.6937e−1
(1.14e−2) −2.8387e−1
(5.11e−4) +2.8468e−1
(1.21e−3) +2.6339e−1
(1.35e−2) −2.5409e−1
(4.07e−2) −NaN
(NaN)2.7750e−1
(1.65e−3) −2.8100e−1
(1.49e−3)DASCMOP8 3 30 IGD+ 4.9027e−2
(3.07e−2) −2.8592e−2
(1.22e−3) −2.9713e−2
(2.59e−3) −3.3574e−1
(1.38e−1) −4.8457e−2
(3.47e−2) −NaN
(NaN)3.6650e−2
(2.27e−3) −2.7787e−2
(2.54e−3)HV 1.8963e−1
(1.30e−2) −2.0385e−1
(5.99e−4) =1.9956e−1
(1.70e−3) −7.5943e−2
(3.27e−2) −1.8823e−1
(2.09e−2) −NaN
(NaN)1.9566e−1
(1.57e−3) −2.0070e−1
(1.25e−3)DASCMOP9 3 30 IGD+ 5.6865e−2
(7.11e−2) −9.0672e−2
(9.83e−2) −1.5676e−1
(9.03e−2) −4.0339e−1
(2.75e−1) −1.3968e−1
(1.03e−1) −4.3114e−1
(1.16e−1) −1.6828e−1
(9.02e−2) −2.1593e−2
(6.94e−4) +HV 1.9154e−1
(2.38e−2) =1.8219e−1
(3.29e−2) −1.5641e−1
(2.99e−2) −6.9845e−2
(5.37e−2) −1.6104e−1
(3.16e−2) −7.1861e−2
(2.98e−2) −1.5291e−1
(2.96e−2) −2.0470e−1
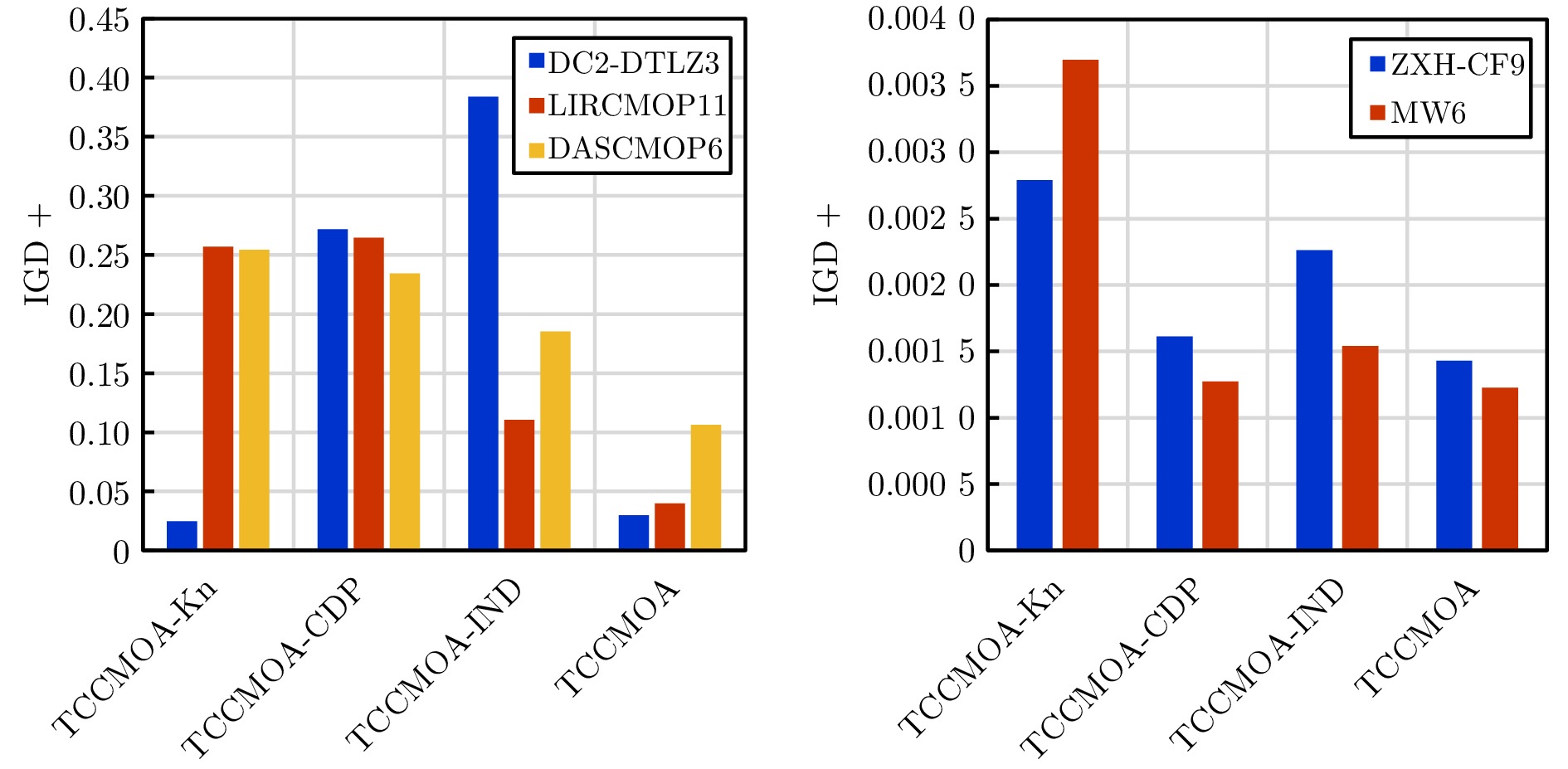
(4.26e−4) ++/−/= 4/10/4 6/9/3 1/15/2 0/18/0 2/15/1 0/18/0 4/12/2
下载: 导出CSV
表 4 参数分析
Table 4 Parameter analysis
TCCMOA vs $\alpha$ $\tau$ HV (+/−/=) IGD+ (+/−/=) TCCMOA1 0.95 0.05 4/8/51 5/12/46 TCCMOA2 0.70 0.05 2/11/50 6/14/43 TCCMOA3 0.50 0.05 3/4/56 4/8/51 TCCMOA4 0.95 0.20 0/8/55 1/6/56 TCCMOA5 0.70 0.20 1/14/48 2/12/49 TCCMOA6 0.50 0.20 4/5/54 3/9/51 TCCMOA7 0.95 0.10 4/11/48 4/11/48 TCCMOA8 0.50 0.10 3/6/54 3/9/51
下载: 导出CSV
表 5 各算法在RWCMOP问题的HV值
Table 5 HV value of each algorithm on the RWCMOP problem
测试问题 $M$ $D$ DCSO DDCMEA DSPCMDE LMOCSO POCEA PPS ToP TCCMOA RWMOP7 2 4 4.8472e−1 (2.17e−5) = 4.8435e−1 (3.10e−5) − 4.8441e−1 (2.56e−5) − 4.8245e−1 (5.35e−5) − 4.8052e−1 (1.08e−3) − 4.8438e−1 (9.20e−5) − 4.8440e−1 (5.11e−5) − 4.8469e−1 (4.43e−5) RWMOP8 3 7 2.5924e−2 (4.30e−5) = 2.5871e−2 (6.39e−5) = 2.5884e−2 (6.08e−5) = 2.1528e−2 (7.62e−4) − 2.0866e−2 (2.11e−3) − 2.4433e−2 (1.04e−3) − 2.5847e−2 (1.04e−4) = 2.5970e−2 (5.08e−5) RWMOP9 2 4 4.0970e−1 (7.69e−5) = 4.0910e−1 (6.18e−5) − 4.0924e−1 (1.94e−4) − 5.4748e−2 (1.62e−3) − 4.0804e−1 (6.49e−4) − 3.8381e−1 (3.85e−3) − 4.0935e−1 (1.33e−4) − 4.0982e−1 (1.20e−4) RWMOP11 5 3 9.2460e−2 (1.40e−3) − 9.2958e−2 (1.24e−3) − 9.6659e−2 (1.17e−3) = 1.8192e−2 (4.24e−3) − 5.9615e−2 (6.51e−3) − 9.7899e−2 (4.15e−4) + 8.9949e−2 (1.20e−3) − 9.5170e−2 (1.66e−3) RWMOP17 3 6 4.0857e−1 (6.38e−4) + 2.6609e−1 (4.10e−3) = 2.6352e−1 (1.23e−2) = 1.3309e−1 (8.79e−2) = 2.3556e−1 (3.54e−2) = 1.7163e−1 (2.81e−2) = 2.2694e−1 (4.61e−2) = 2.0382e−1 (6.14e−2) RWMOP18 2 3 4.0516e−2 (2.80e−6) − 4.0494e−2 (3.03e−6) − 4.0496e−2 (5.15e−6) − 4.0385e−2 (9.89e−5) − 4.0254e−2 (4.83e−5) − 4.0480e−2 (7.78e−6) − 4.0494e−2 (4.75e−6) − 4.0522e−2 (3.25e−6) RWMOP21 2 6 3.1757e−2 (1.37e−6) − 3.1756e−2 (9.66e−7) − 3.1757e−2 (8.28e−7) − 2.9352e−2 (1.84e−5) − 3.1728e−2 (7.89e−6) − 3.1630e−2 (2.51e−5) − 3.1756e−2 (1.17e−6) − 3.1762e−2 (8.52e−7) RWMOP23 2 6 6.8732e−1 (2.34e−1) − 9.0073e−1 (2.24e−1) = NaN (NaN) NaN (NaN) 9.1298e−1 (4.01e−2) = 8.5640e−1 (8.91e−3) = 6.0346e−1 (3.75e−1) = 9.5068e−1 (8.37e−2) RWMOP28 2 7 1.5876e−2 (3.31e−3) = 1.4693e−2 (1.61e−2) = NaN (NaN) NaN (NaN) NaN (NaN) 1.8276e−2 (6.63e−3) = NaN (NaN) 3.3407e−2 (0.00e+0) RWMOP50 2 6 7.5498e−3 (5.95e−4) = 8.0262e−3 (5.33e−4) = 4.7465e−3 (2.58e−3) − NaN (NaN) NaN (NaN) 4.8280e−3 (1.19e−3) − 7.6154e−3 (7.03e−4) = 8.1628e−3 (2.28e−4) +/−/= 1/4/5 0/5/5 0/7/3 0/9/1 0/8/2 1/6/3 0/5/5
下载: 导出CSV
-
[1] Chen Y F, Wang R, Ming M J, Cheng S, Bao Y P, Zhang W S, et al. Constraint multi-objective optimal design of hybrid renewable energy system considering load characteristics. Complex Intelligent Systems, 2022, 8(2): 803−817 doi: 10.1007/s40747-021-00363-4 [2] Hou Y, Shen Y, Han H, Wu Y, Huang Y. Adaptive constrained multi-objective differential evolution algorithm for vehicle routing problem considering crowdsourcing delivery. Applied Soft Computing, 2025, 169: Article No. 112517 doi: 10.1016/j.asoc.2024.112517 [3] Boeckmann J, Thielen C, Pferschy U. Approximating single- and multi-objective nonlinear sum and product knapsack problems. Discrete Optimization, 2023, 48: Article No. 100771 doi: 10.1016/j.disopt.2023.100771 [4] Zhang X, Ma Z B, Ding B W, Fang W, Qian P J. A coevolutionary algorithm based on the auxiliary population for constrained large-scale multi-objective supply chain network. Mathematical Biosciences and Engineering, 2022, 19(1): 271−286 doi: 10.3934/mbe.2022014 [5] Zhang X, Han Z, Wang Z, Zhao J, Wang W. Ingredient planning for copper Industry: A deep reinforcement learning-based ϵ-constrained multi-objective optimization framework. In: Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC). Yokohama, Japan: IEEE, 2024. 1−8 [6] Hua Y, Liao B, Zhang H, Liu L, Li Y, Yang Y. Optimal scheduling of microgrid using constrained multi-objective optimization with additional objectives. In: Proceedings of the 6th International Conference on Data-driven Optimization of Complex Systems (DOCS). Hangzhou, China: IEEE, 2024. 501−506 [7] Liang J, Ban X, Yu K, Qu B, Qiao K, Yue C, et al. A survey on evolutionary constrained multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2023, 27(2): 201−221 doi: 10.1109/TEVC.2022.3155533 [8] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197 doi: 10.1109/4235.996017 [9] Jia W, Huang T, Qin S. A collective neurodynamic penalty approach to nonconvex distributed constrained optimization. Neural Networks, 2024, 171: 145−158 doi: 10.1016/j.neunet.2023.12.011 [10] Fan Z, Li W, Cai X, Li H, Wei C, Zhang Q, et al. Push and pull search for solving constrained multi-objective optimization problems. Swarm and Evolutionary Computation, 2019, 44: 665−679 doi: 10.1016/j.swevo.2018.08.017 [11] Tian Y, Wang R, Zhang Y, Zhang X. Adaptive population sizing for multi-population based constrained multi-objective optimization. Neurocomputing, 2025, 621: Article No. 129296 doi: 10.1016/j.neucom.2024.129296 [12] Zhao S, Hao X, Chen L, Yu T, Li X, Liu W. Two-stage bidirectional coevolutionary algorithm for constrained multi-objective optimization. Swarm and Evolutionary Computation, 2025, 92: Article No. 101784 doi: 10.1016/j.swevo.2024.101784 [13] Yu K, Liang J, Qu B, Luo Y, Yue C. Dynamic selection preference-assisted constrained multiobjective differential evolution. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 52(5): 2954−2965 [14] Yu Q Q, Yang C, Dai G M, Peng L, Li J. A novel penalty function-based interval constrained multi-objective optimization algorithm for uncertain problems. Swarm and Evolutionary Computation, 2024, 88: Article No. 101584 doi: 10.1016/j.swevo.2024.101584 [15] Zhou P, Zhang S, Chai T. Adaptive constraint penalty-based multiobjective operation optimization of an industrial dynamic system with complex multiconstraint. IEEE Transactions on Cybernetics, 2024, 54(8): 4724−4737 doi: 10.1109/TCYB.2023.3341982 [16] Song S, Zhang K, Zhang L, Wu N. A dual-population algorithm based on self-adaptive epsilon method for constrained multi-objective optimization. Information Sciences, 2024, 655: Article No. 119906 doi: 10.1016/j.ins.2023.119906 [17] Ji J Y, Zeng S, Wong M L. ϵ-constrained multiobjective differential evolution using linear population size expansion. Information Sciences, 2022, 609: 445−464 doi: 10.1016/j.ins.2022.07.108 [18] Wang Y, Wang H, Razzaghi R, Jalili M, Liebman A. Multi-objective coordinated EV charging strategy in distribution networks using an improved augmented epsilon-constrained method. Applied Energy, 2024, 39: Article No. 123547 [19] Qiao K, Liang J, Liu Z, Yu K, Yue C, Qu B. Evolutionary multitasking with global and local auxiliary tasks for constrained multi-objective optimization. IEEE/CAA Journal of Automatica Sinica, 2023, 10(10): 1951−1964 doi: 10.1109/JAS.2023.123336 [20] Che W, Zheng J, Hu Y, Zou J, Yang S. Dynamic constrained multi-objective optimization algorithm based on co-evolution and diversity enhancement. Swarm and Evolutionary Computation, 2024, 89: Article No. 101639 doi: 10.1016/j.swevo.2024.101639 [21] Long W, Dong H, Wang P, Huang Y, Li J, Yang X, et al. A constrained multi-objective optimization algorithm using an efficient global diversity strategy. Complex & Intelligent Systems, 2023, 9(2): 1455−1478 [22] Ming F, Gong W, Wang L, Lu C. A tri-population based co-evolutionary framework for constrained multi-objective optimization problems. Swarm and Evolutionary Computation, 2022, 70: Article No. 101055 doi: 10.1016/j.swevo.2022.101055 [23] Zou J, Sun R, Yang S, Zheng J. A dual-population algorithm based on alternative evolution and degeneration for solving constrained multi-objective optimization problems. Information Sciences, 2021, 579: 89−102 doi: 10.1016/j.ins.2021.07.078 [24] 慈雨, 荣淼, 彭晨. 基于双重距离的多目标粒子群优化算法. 控制与决策, 2024, 39(6): 1801−1809Ci Yu, Rong Miao, Peng Chen. Multi-objective particle awarm optimization algorithm based on dual distances. Control and Decision, 2024, 39(6): 1801−1809 [25] 张伟, 黄卫民. 基于种群分区的多策略自适应多目标粒子群算法. 自动化学报, 2022, 48(10): 2585−2599Zhang Wei, Huang Wei-Min. Multi-strategy adaptive multi-objective particle swarm optimization algorithm based on swarm partition. Acta Automatica Sinica, 2022, 48(10): 2585−2599 [26] 陈莹, 黄佩萱, 陈锦萍, 王祖怡, 沈映珊, 樊小毛. 基于分层学习和差分进化的混合PSO算法求解车辆路径问题. 计算机科学, 2022, 49(S2): 188−194Chen Ying, Huang Pei-Xuan, Chen Jin-Ping, Wang Zu-Yi, Shen Ying-Shan, Fan Xiao-Mao. Hybrid particle swarm optimization algorithm based on hierarchical learning and different evolution for solving capacitated vehicle routing problem. Computer Science, 2022, 49(S2): 188−194 [27] Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization. IEEE Transactions on Cybernetics, 2014, 45(2): 191−204 [28] Tian Y, Zheng X, Zhang X, Jin Y. Efficient large-scale multiobjective optimization based on a competitive swarm optimizer. IEEE Transactions on Cybernetics, 2019, 50(8): 3696−3708 [29] Li K, Chen R, Fu G, Yao X. Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2018, 23(2): 303−315 [30] 袁志超, 杨磊, 田井林, 魏晓威, 李康顺. 面向复杂约束多目标优化问题的双种群双阶段进化算法. 计算机应用, DOI: 10.11772/j.issn.1001-9081.2024081130Yuan Zhi-Chao, Yang Lei, Tian Jing-Lin, Wei Xiao-Wei, Li Kang-Shun. Dual-population dual-stage evolutionary algorithm for complex constrained multiobjective optimization problems. Journal of Computer Applications, DOI: 10.11772/j.issn.1001-9081.2024081130 [31] Li W, Gong W, Ming F, Wang L. Constrained multi-objective evolutionary algorithm with an improved two-archive strategy. Knowledge-Based Systems, 2022, 246: Article No. 108732 doi: 10.1016/j.knosys.2022.108732 [32] Wang Q, Li Y, Hou Z, Zou J, Zheng J. A novel multi-population evolutionary algorithm based on hybrid collaboration for constrained multi-objective optimization. Swarm and Evolutionary Computation, 2024, 87: Article No. 101581 doi: 10.1016/j.swevo.2024.101581 [33] Ming M J, Trivedi A, Wang R, Srinivasan D, Zhang T. A dual-population-based evolutionary algorithm for constrained multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2021, 25(4): 739−753 doi: 10.1109/TEVC.2021.3066301 [34] Liu Z Z, Wang B C, Tang K. Handling constrained multiobjective optimization problems via bidirectional coevolution. IEEE Transactions on Cybernetics, 2021, 52(10): 10163−10176 [35] Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Report, 2001, 103: 1−22 [36] Cui X, Zhang H, He J. Multi-subpopulation coevolutionary algorithm with adaptive Cauchy-Polynomial mutation. In: Proceedings of the 40th Chinese Control Conference (CCC). Shanghai, China: IEEE, 2021. 1651−1656 [37] Cheng R, Jin Y, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773−791 doi: 10.1109/TEVC.2016.2519378 [38] Kumar A, Wu G, Ali M Z, Luo Q, Mallipeddi R, Suganthan P N, et al. A benchmark-suite of real-world constrained multi-objective optimization problems and some baseline results. Swarm and Evolutionary Computation, 2021, 67: Article No. 100961 doi: 10.1016/j.swevo.2021.100961 [39] Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. Evolutionary Multiobjective Optimization: Theoretical Advances and Applications. London: Springer, 2005. 105−145 [40] Zhou Y, Xiang Y, He X. Constrained multiobjective optimization: Test problem construction and performance evaluations. IEEE Transactions on Evolutionary Computation, 2020, 25(1): 172−186 [41] Fan Z, Li W, Cai X, Huang H, Fang Y, You Y, et al. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions. Soft Computing, 2019, 23: 12491−12510 doi: 10.1007/s00500-019-03794-x [42] Fan Z, Li W, Cai X, Li H, Wei C, Zhang Q, et al. Difficulty adjustable and scalable constrained multiobjective test problem toolkit. Evolutionary Computation, 2020, 28(3): 339−378 doi: 10.1162/evco_a_00259 [43] Ma Z, Wang Y. Evolutionary constrained multiobjective optimization: Test suite construction and performance comparisons. IEEE Transactions on Evolutionary Computation, 2019, 23(6): 972−986 doi: 10.1109/TEVC.2019.2896967 [44] Ishibuchi H, Masuda H, Tanigaki Y, Nojima Y. Modified distance calculation in generational distance and inverted generational distance. In: Proceedings of the 8th International Conference on Evolutionary Multi-Criterion Optimization. Guimares, Portugal: IEEE, 2015. 110−125 [45] Zitzler E, Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257−271 doi: 10.1109/4235.797969 [46] Wilcoxon F, Bulletin S B, Dec N. Individual comparisons by ranking methods. Springer New York, 1992, DOI: 10.1007/978-1-4612-4380-916 [47] Wang Y, Hu C, Gong W, Ming F. Constrained multi-objective optimization with dual-swarm assisted competitive swarm optimizer. Swarm and Evolutionary Computation, 2024, 86: Article No. 101496 doi: 10.1016/j.swevo.2024.101496 [48] Kong X, Yang Y, Lv Z, Zhao J, Fu R. A dynamic dual-population co-evolution multi-objective evolutionary algorithm for constrained multi-objective optimization problems. Applied Soft Computing, 2023, 141: Article No. 110311 doi: 10.1016/j.asoc.2023.110311 [49] Sun R, Zou J, Liu Y, Yang S, Zheng J. A multistage algorithm for solving multiobjective optimization problems with multiconstraints. IEEE Transactions on Evolutionary Computation, 2022, 27(5): 1207−1219 [50] Liu Z Z, Wang Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Transactions on Evolutionary Computation, 2019, 23(5): 870−884 doi: 10.1109/TEVC.2019.2894743 [51] Pan L, Xu W, Li L, He C, Cheng R. Adaptive simulated binary crossover for rotated multi-objective optimization. Swarm and Evolutionary Computation, 2021, 60: Article No. 100759 doi: 10.1016/j.swevo.2020.100759 [52] He C, Cheng R, Tian Y, Zhang X, Tan K C, Jin Y. Paired offspring generation for constrained large-scale multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2020, 25(3): 448−462 -
计量
- 文章访问数: 4
- HTML全文浏览量: 2
- 被引次数: 0
