松弛图嵌入的判别宽度学习系统以及在视觉识别中的应用

金军委; 常少凯; 耿彪; 李艳婷; 赵孟; 王震; 陈俊龙; 李鹏

doi:10.16383/j.aas.c240734

松弛图嵌入的判别宽度学习系统以及在视觉识别中的应用

doi: 10.16383/j.aas.c240734 cstr: 32138.14.j.aas.c240734

金军委^1,,
常少凯^1,,
耿彪^1,,
李艳婷^2,,
赵孟^1,,
王震^3,,
陈俊龙^4,,
李鹏^5,

1.
河南工业大学人工智能与大数据学院郑州 450001
2.
郑州轻工业大学计算机科学与技术学院郑州 450001
3.
西北工业大学网络空间安全学院西安 710072
4.
华南理工大学计算机科学与工程学院广州 510641
5.
河南工业大学复杂性科学研究院郑州 450001

基金项目: 国家自然科学基金(62106068, 62106233, 62073123, 62375078, U1813203), 河南省科技攻关项目(222102210058, 232102210062, 232102210007)资助

详细信息

作者简介:
金军委：河南工业大学人工智能与大数据学院副教授. 主要研究方向为机器学习, 计算机视觉和神经网络. 本文通信作者. E-mail: jinjunwei24@163.com

常少凯：河南工业大学人工智能与大数据学院硕士研究生. 主要研究方向为计算机视觉, 标签增强和宽度学习. E-mail: csk4188@163.com

耿彪：河南工业大学人工智能与大数据学院本科生, 主要研究方向为神经网络, 机器学习和计算机视觉. E-mail: gengbiao2002@163.com

李艳婷：郑州轻工业大学计算机科学与技术学院讲师. 主要研究方向为函数逼近理论, 图像处理, 稀疏编码和机器学习. E-mail: ytli1227@126.com

赵孟：河南工业大学人工智能与大数据学院讲师. 主要研究方向为人机对话系统, 生成式人工智能和自然语言处理. E-mail: zm@haut.edu.cn

王震：西北工业大学网络空间安全学院教授. 主要研究方向为复杂网络, 进化博弈和数据科学. E-mail: w-zhen@nwpu.edu.cn

陈俊龙：华南理工大学计算机科学与工程学院教授. 主要研究方向为控制论, 系统和计算智能. E-mail: philip.chen@ieee.org

李鹏：河南工业大学复杂性科学研究院教授. 主要研究方向为中医大数据和人工智能. E-mail: lipeng@haut.edu.cn

计量
- 文章访问数: 98
- HTML全文浏览量: 47
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-13
- 录用日期: 2025-04-10
- 网络出版日期: 2025-05-01

Relaxed-graph Embedding Discriminative Broad Learning System andIts Application in Visual Recognition

1.
School of Artificial Intelligence and Big Data, Henan University of Technology, Zhengzhou 450001
2.
School of Computer Science and Technology, Zhengzhou University of Light Industry, Zhengzhou 450001
3.
School of Cybersecurity, Northwestern Polytechnical University, Xi＇an 710072
4.
School of Computer Science and Engineering, South China University of Technology, Guangzhou 510641
5.
Institute for Complexity Science, Henan University of Technology, Zhengzhou 450001

Funds: Supported by National Natural Science Foundation of China (62106068, 62106233, 62073123, 62375078, U1813203), and Science and Technology Research Project of Henan Province (222102210058, 232102210062, 232102210007)

More Information

Author Bio:
JIN Jun-Wei　Associate professor at the School of Artificial Intelligence and Big Data, Henan University of Technology. His research interest covers machine learning, computer vision, and neural networks. Corresponding author of this paper

CHANG Shao-Kai　Master student at the School of Artificial Intelligence and Big Data, Henan University of Technology. His research interest covers computer vision, label enhancement, and broad learning

GENG Biao　Undergraduate at the School of Artificial Intelligence and Big Data, Henan University of Technology. His research interest covers neural networks, machine learning, and computer vision

LI Yan-Ting　Lecturer at the School of Computer Science and Technology, Zhengzhou University of Light Industry. Her research interest covers function approximation theory, image processing, sparse coding, and machine learning

ZHAO Meng　Lecturer at the School of Artificial Intelligence and Big Data, Henan University of Technology. His main research interest is dialogue systems, generative artificial intelligence, and natural language processing

WANG Zhen　Professor at the School of Cybersecurity, Northwestern Polytechnical University. His research interest covers complex networks, evolutionary game, and data science

CHEN C. L. Philip　Professor at the School of Computer Science and Engineering, South China University of Technology. His research interest covers cybernetics, systems, and computational intelligence

LI Peng　Professor at the Institute for Complexity Science, Henan University of Technology. His research interest covers big data and artificial intelligence in traditional Chinese medicine

摘要

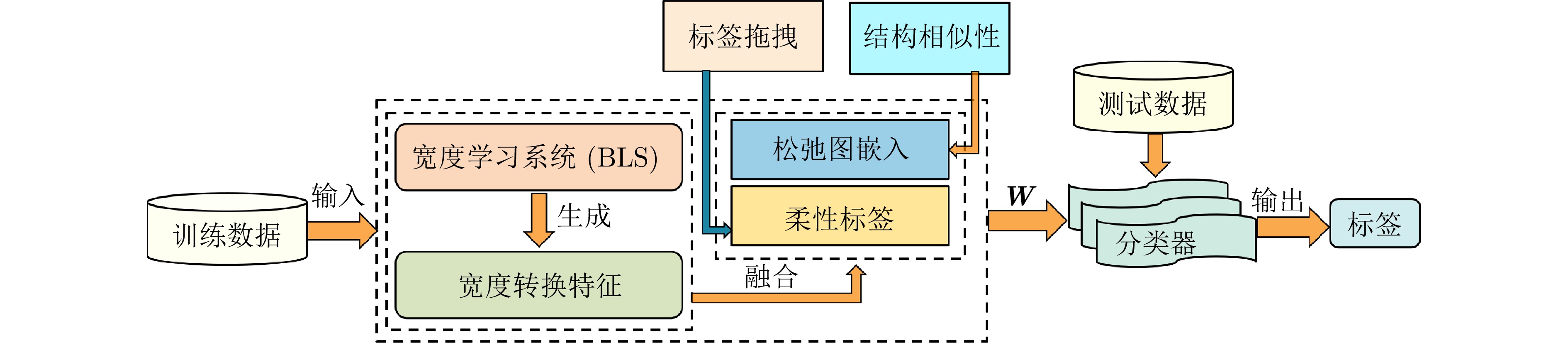
摘要: 宽度学习系统作为一种轻量级网络, 在效率和准确性之间实现了良好的平衡. 然而, 宽度学习系统主要依赖严苛的二元标签进行监督并且在数据变换过程中忽视局部结构信息, 这些问题限制了模型的性能. 为解决此问题, 提出一种松弛图嵌入的判别宽度学习系统模型并将其应用于视觉识别, 旨在通过松弛图结构与柔性标签的引入提升模型性能. 创新性如下: 1)创新地使用双变换矩阵构建松弛图, 将变换矩阵的责任分离, 减少变换矩阵的负担, 从而学习更加灵活的变换矩阵, 解决了模型过拟合问题; 2)引入柔性标签策略, 扩大不同类别标签之间的距离, 解决了严苛二元标签的问题, 提高了模型的判别能力; 3)提出一种基于交替方向乘子法的迭代优化算法, 实现了模型的高效优化. 在人脸图像数据集、物体图像数据集、场景图像数据集以及手写体图像数据集上的大量实验证明提出的模型与其他先进的识别算法相比具有优势.
- 宽度学习系统 /
- 松弛图 /
- 柔性标签 /
- 视觉识别
Abstract: The broad learning system, as a lightweight network, achieves a good balance between efficiency and accuracy. However, it primarily relies on strict binary labels for supervision and neglects local structural information during data transformation, limiting the model＇s performance. To address this issue, this paper proposes a relaxed-graph embedding discriminative broad learning system model and applies it to visual recognition, with the goal of enhancing model performance through the introduction of flexible labels and a relaxed-graph structure. The innovations of this paper are as follows: 1) We innovatively use double transformation matrices to construct the relaxed-graph, separating the responsibilities of the transformation matrix. This reduces the burden on the transformation matrix and allows for the learning of more flexible transformation matrix, thereby mitigating the overfitting problem; 2) We introduce a flexible label strategy that increases the distance between different categories labels, addressing the issue of strict binary labels, and thereby enhancing the model＇s discriminative ability; 3) An iterative optimization algorithm based on the alternating direction method of multipliers is proposed to achieve efficient model optimization. Extensive experiments on facial image datasets, object image datasets, scene image datasets, and handwritten character image datasets demonstrate that the proposed model outperforms other advanced recognition algorithms.
- Broad learning system /
- relaxed-graph /
- flexible label /
- visual recognition

HTML全文

图 1 标准宽度学习系统网络架构

Fig. 1 The network structure of the standard broad learning system

下载: 全尺寸图片幻灯片

图 2 DREBLS模型的流程图

Fig. 2 Flowchart of DREBLS model

下载: 全尺寸图片幻灯片

图 3 部分人脸数据集图像

Fig. 3 Some images of face datasets

下载: 全尺寸图片幻灯片

图 4 场景与物体数据集部分图像

Fig. 4 Some images of scene and object datasets

下载: 全尺寸图片幻灯片

图 5 手写体数据集部分图像

Fig. 5 Some images of handwritten character datasets

下载: 全尺寸图片幻灯片

图 6 分类准确率(%)和目标函数值随迭代次数的变化曲线

Fig. 6 Variation curves of the classification accuracy (%) and objective function values versus the number of iterations

下载: 全尺寸图片幻灯片

图 7 正则化参数$ \lambda_1 $和$ \lambda_2 $选用不同值时的分类准确率(%)

Fig. 7 Classification accuracy (%) of different values of regularization parameters $ \lambda_1 $ and $ \lambda_2 $

下载: 全尺寸图片幻灯片

图 8 矩阵$ \boldsymbol{T} $在不同数据集的可视化效果

Fig. 8 Visualization effects of matrix $ \boldsymbol{T} $ in different datasets

下载: 全尺寸图片幻灯片

图 9 不同算法在Fifteen Scenes数据集上的转换特征进行t-SNE可视化

Fig. 9 The t-SNE visualization of transformed features by different algorithms on the Fifteen Scenes dataset

下载: 全尺寸图片幻灯片

图 10 不同算法在AR数据集上的转换特征进行t-SNE可视化

Fig. 10 The t-SNE visualization of transformed features by different algorithms on the AR dataset

下载: 全尺寸图片幻灯片

图 11 Calinski-Harabasz与Davies-Bouldin指数量化分析

Fig. 11 Quantitative analysis using the Calinski-Harabasz index and Davies-Bouldin index

下载: 全尺寸图片幻灯片

表 1 实验中使用的6个数据集的简要信息

Table 1 The brief information of the 6 datasets used in the experiments

数据集	样本总数量	维度	类别数
Extended YaleB	$ 2\ 414 $	$ 1\ 024 $	$ 38 $
AR	$ 2\ 600 $	$ 540 $	$ 100 $
Fifteen Scenes	$ 4\ 485 $	$ 3\ 000 $	$ 15 $
COIL100	$ 7\ 200 $	$ 1\ 024 $	$ 100 $
MNIST	$ 70\ 000 $	$ 784 $	$ 10 $
USPS	$ 9\ 298 $	$ 256 $	$ 10 $

下载: 导出CSV

表 2 Extended YaleB数据集不同方法的分类准确率以及标准差

Table 2 Classification accuracy and standard deviation of different methods on the Extended YaleB dataset

算法	10 样本	15 样本	20 样本	25 样本
SRC	87.8 ± 0.3	92.6 ± 0.6	94.4 ± 0.6	96.7 ± 0.5
CRC	86.1 ± 0.5	90.7 ± 0.3	93.0 ± 0.2	94.1 ± 0.3
LRC	83.3 ± 0.4	89.4 ± 0.5	92.4 ± 0.2	93.6 ± 0.3
TDDL	84.3 ± 0.6	88.9 ± 0.3	92.5 ± 0.4	95.0 ± 0.6
Robust PCA	86.1 ± 0.2	90.5 ± 0.4	93.5 ± 0.6	95.4 ± 0.3
LatLRR	84.0 ± 0.5	88.8 ± 0.3	92.1 ± 0.5	93.8 ± 0.6
SVM	81.5 ± 1.4	89.2 ± 0.9	92.6 ± 0.7	94.5 ± 0.6
ELM	85.5 ± 0.2	91.2 ± 0.6	93.7 ± 0.4	95.2 ± 0.5
RF	83.4 ± 0.4	88.5 ± 0.3	91.1 ± 0.5	94.6 ± 0.4
RLR	88.4 ± 0.3	92.8 ± 0.4	96.1 ± 0.3	97.5 ± 0.2
DLSR	86.2 ± 0.9	92.3 ± 0.7	94.7 ± 0.7	95.8 ± 0.4
LRLR	78.2 ± 1.7	82.0 ± 0.9	83.8 ± 1.5	85.0 ± 1.0
SLRR	78.0 ± 1.7	82.3 ± 1.0	84.2 ± 0.7	85.1 ± 1.1
LRSI	87.1 ± 0.6	92.7 ± 0.5	94.2 ± 0.3	96.1 ± 0.5
CBDS	85.8 ± 1.8	93.1 ± 1.3	95.8 ± 1.0	96.3 ± 0.8
DRAGD	88.8 ± 0.7	94.2 ± 0.5	96.7 ± 0.4	97.6 ± 0.4
FRBLS	88.9 ± 1.4	93.0 ± 1.1	95.3 ± 0.6	96.2 ± 0.7
LDMBLS	88.1 ± 1.4	93.3 ± 0.9	96.6 ± 0.8	97.4 ± 1.2
DREBLS	89.0 ± 0.8	94.3 ± 0.6	97.0 ± 0.9	97.9 ± 0.6

下载: 导出CSV

表 3 AR数据集不同方法的分类准确率

Table 3 Classification accuracies of different methods on the AR dataset

算法	准确率(%)
K-SVD^[37] (每人5个样本)	86.5
D-SVD^[37] (每人5个样本)	88.8
CRC	97.3
LRC	94.5
LC-KSVD1^[37] (每人5个样本)	92.5
LC-KSVD2^[37] (每人5个样本)	93.7
LC-KSVD2^[37] (所有训练样本)	97.8
SVM	96.7
RLR	98.1
LatLRR	97.6
ELM	96.4
DLSR	97.6
DRAGD	99.0
FRBLS	99.0
LDMBLS	98.3
DREBLS	99.2

下载: 导出CSV

表 4 Fifteen Scenes数据集不同方法的分类准确率

Table 4 Classification accuracies of different methods on the Fifteen Scenes dataset

算法	准确率(%)	算法	准确率(%)
LLC	79.4	Robust PCA	92.1
LLC*^[37]	89.2	Lazebnik^[37]	81.4
LRC	91.9	SVM	93.6
LRSIC	92.4	RLR	96.8
LRRC	90.1	Yang^[37]	80.3
SLRRC	91.3	Lian^[37]	86.4
Boureau^[37]	84.3	LC-KSVD1^[37]	90.4
LC-KSVD2^[37]	92.9	DLSR	95.9
ELM	94.5	CBDS	95.7
Gemert^[37]	76.7	LRLR	94.5
LRRR	88.1	SLRR	89.6
DRAGD	98.4	FRBLS	98.4
LDMBLS	98.3	DREBLS	98.5

下载: 导出CSV

表 5 COIL100数据集不同方法的分类准确率以及标准差

Table 5 Classification accuracy and standard deviation of different methods on the COIL100 dataset

算法	10样本	15样本	20样本	25样本
SRC	80.4 ± 0.6	86.1 ± 0.8	89.4 ± 0.4	91.9 ± 0.4
CRC	76.2 ± 0.6	81.3 ± 0.4	84.2 ± 0.5	86.3 ± 0.5
LRC	79.9 ± 0.7	85.3 ± 0.6	88.7 ± 0.7	91.0 ± 0.5
TDDL	83.3 ± 0.6	87.9 ± 0.3	90.8 ± 0.4	90.0 ± 0.7
Robust PCA	82.5 ± 0.6	88.3 ± 0.8	91.7 ± 0.3	93.5 ± 0.3
LatLRR	79.6 ± 0.5	85.3 ± 0.4	88.4 ± 0.4	90.7 ± 0.4
SVM	79.2 ± 0.5	84.8 ± 0.6	88.1 ± 0.4	90.8 ± 0.6
ELM	81.2 ± 0.4	85.6 ± 0.7	89.7 ± 0.4	92.1 ± 0.6
RF	84.3 ± 0.5	88.3 ± 0.5	91.1 ± 0.5	93.3 ± 0.5
RLR	80.1 ± 0.6	83.4 ± 0.7	85.9 ± 0.8	87.2 ± 0.6
DLSR	84.8 ± 0.5	88.0 ± 0.5	90.1 ± 0.3	92.0 ± 0.4
LRLR	66.2 ± 0.8	71.2 ± 0.6	73.7 ± 0.8	75.7 ± 0.7
SLRR	69.1 ± 0.8	73.0 ± 0.6	74.5 ± 0.6	75.9 ± 0.7
LRSI	79.7 ± 0.5	87.8 ± 0.3	91.4 ± 0.4	93.6 ± 0.6
CBDS	73.7 ± 0.5	78.6 ± 0.8	80.9 ± 0.7	81.3 ± 0.5
DRAGD	83.5 ± 0.5	88.6 ± 0.4	94.8 ± 0.3	96.0 ± 0.3
FRBLS	84.8 ± 0.7	90.2 ± 0.6	94.7 ± 0.7	96.4 ± 0.5
LDMBLS	83.6 ± 1.1	89.3 ± 1.3	94.0 ± 0.9	96.1 ± 1.0
DREBLS	86.0 ± 0.5	91.0 ± 0.6	95.1 ± 0.6	97.2 ± 0.6

下载: 导出CSV

表 6 BLS、LDMBLS和DREBLS方法在USPS数据集上的分类准确率及标准差

Table 6 Classification accuracy and standard deviation of BLS, LDMBLS and DREBLS methods on the USPS dataset

样本数量	BLS				LDMBLS				DREBLS
样本数量	$ N_g $	$ N_f $	$ m $	准确率(%)	$ N_g $	$ N_f $	$ m $	准确率(%)	$ N_g $	$ N_f $	$ m $	准确率(%)
$ 100 $	$ 5 $	$ 15 $	$ 180 $	$ 90.88\pm0.56 $	$ 10 $	$ 10 $	$ 150 $	$ 94.45\pm0.65 $	$ 10 $	$ 15 $	$ 150 $	$ \boldsymbol{94.71\pm0.79} $
$ 150 $	$ 10 $	$ 20 $	$ 300 $	$ 92.62\pm0.87 $	$ 10 $	$ 15 $	$ 200 $	$ 95.38\pm0.37 $	$ 10 $	$ 20 $	$ 200 $	$ \boldsymbol{95.58\pm0.64} $
$ 200 $	$ 20 $	$ 30 $	$ 500 $	$ 93.37\pm0.68 $	$ 15 $	$ 20 $	$ 400 $	$ 96.23\pm0.31 $	$ 18 $	$ 25 $	$ 420 $	$ \boldsymbol{96.70\pm0.52} $
$ 250 $	$ 20 $	$ 40 $	$ 1\ 200 $	$ 94.08\pm0.50 $	$ 20 $	$ 30 $	$ 1\ 000 $	$ 96.99\pm0.59 $	$ 25 $	$ 30 $	$ 1\ 100 $	$ \boldsymbol{97.40\pm0.42} $

下载: 导出CSV

表 7 BLS、LDMBLS和DREBLS方法在MNIST数据集上的分类准确率及标准差

Table 7 Classification accuracy and standard deviation of BLS, LDMBLS and DREBLS methods on the MNIST dataset

样本数量	BLS				LDMBLS				DREBLS
样本数量	$ N_g $	$ N_f $	$ m $	准确率(%)	$ N_g $	$ N_f $	$ m $	准确率(%)	$ N_g $	$ N_f $	$ m $	准确率(%)
$ 100 $	$ 7 $	$ 15 $	$ 500 $	$ 90.80\pm0.85 $	$ 8 $	$ 10 $	$ 400 $	$ 92.16\pm0.41 $	$ 10 $	$ 10 $	$ 400 $	$ \boldsymbol{92.91\pm0.87} $
$ 300 $	$ 25 $	$ 40 $	$ 1\ 200 $	$ 94.04\pm0.88 $	$ 20 $	$ 35 $	$ 1\ 000 $	$ 94.95\pm0.51 $	$ 30 $	$ 30 $	$ 1\ 000 $	$ \boldsymbol{95.06\pm0.23} $
$ 500 $	$ 30 $	$ 40 $	$ 1\ 500 $	$ 95.94\pm0.52 $	$ 30 $	$ 35 $	$ 1\ 300 $	$ 96.06\pm0.19 $	$ 30 $	$ 38 $	$ 1\ 200 $	$ \boldsymbol{96.16\pm0.15} $
$ 800 $	$ 30 $	$ 50 $	$ 2\ 000 $	$ 96.96\pm0.47 $	$ 30 $	$ 45 $	$ 1\ 500 $	$ 96.67\pm0.11 $	$ 40 $	$ 40 $	$ 1\ 800 $	$ \boldsymbol{96.99\pm0.15} $

下载: 导出CSV

表 8 BLS、LDMBLS、DREBLS*及DREBLS方法在Fifteen Scenes数据集上的分类多指标评估

Table 8 Classification multi-metric evaluation of BLS, LDMBLS, DREBLS* and DREBLS methods on Fifteen Scenes dataset

指标	算法	类别1	类别2	类别3	类别4	类别5	类别6	类别7	类别8	类别9	类别10	平均值
准确率	BLS	93.2	94.4	88.3	92.9	86.5	92.4	95.9	96.3	83.6	100.0	92.0
	LDMBLS	98.6	95.9	95.8	90.8	100.0	97.5	98.5	99.3	89.3	98.5	95.5
	DREBLS*	96.4	92.9	88.3	93.8	99.0	92.1	97.0	97.4	92.2	97.4	94.5
	DREBLS	96.8	97.4	98.7	94.6	99.0	97.7	99.5	99.6	95.8	98.5	97.3
召回率	BLS	98.6	98.2	98.6	99.6	94.3	97.9	99.2	100.0	100.0	50.1	94.8
	LDMBLS	98.6	98.2	98.6	99.6	94.3	97.9	99.2	100.0	100.0	50.1	94.8
	DREBLS*	98.6	99.1	87.5	97.0	82.4	96.5	100.0	100.0	96.0	88.4	94.5
	DREBLS	99.1	98.2	95.3	100.0	92.5	97.7	99.2	100.0	98.8	99.0	98.0
F1分数	BLS	95.8	96.3	93.2	96.1	90.2	95.1	97.5	98.1	90.9	66.8	94.0
	LDMBLS	98.2	97.5	95.5	94.9	94.0	96.5	99.2	98.7	94.0	93.4	95.2
	DREBLS*	97.5	96.0	87.9	95.3	89.9	94.2	98.3	99.0	94.1	92.7	94.0
	DREBLS	97.9	97.8	97.0	97.0	95.6	97.7	99.4	100.0	97.3	98.7	98.0

下载: 导出CSV

表 9 算法运行的时间效率对比

Table 9 Time efficiency comparison of algorithm execution

数据集	算法	训练时间(s)	测试时间(s)	准确率(%)
AR	BLS	2.407 0	0.497 8	95.4
	LDMBLS	3.973 9	0.628 4	98.3
	DREBLS*	3.640 5	0.599 3	98.0
	DREBLS	3.847 8	0.598 9	99.2
COIL100	BLS	1.795 7	0.305 4	82.5
	LDMBLS	2.796 8	0.476 9	89.3
	DREBLS*	2.181 7	0.424 1	86.6
	DREBLS	2.872 8	0.432 3	91.0
USPS	BLS	1.692 4	0.342 4	92.6
	LDMBLS	2.873 9	0.448 8	95.4
	DREBLS*	2.556 1	0.401 5	93.7
	DREBLS	2.596 8	0.403 5	95.6

下载: 导出CSV

参考文献(38)

[1]	He M, Zhang J, Shan S, Chen X. Enhancing face recognition with detachable self-supervised bypass networks. IEEE Transactions on Image Processing, 2024, 33: 1588−1599 doi: 10.1109/TIP.2024.3364067
[2]	Sun Z, Ke Q, Rahmani H, Bennamoun M, Wang G, Liu J. Human action recognition from various data modalities: A review. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(3): 3200−3225
[3]	Huang H, Oh S K, Fu Z, Wu C, Pedrycz W, Kim J Y. FSCNN: Fuzzy channel filter-based separable convolution neural networks for medical imaging recognition. IEEE Transactions on Fuzzy Systems, 2024, 32(10): 5449−5461 doi: 10.1109/TFUZZ.2024.3450000
[4]	Cheng X, He X, Qiao M, Li P, Chang P, Zhang T, et al. Multi-view graph convolutional network with spectral component decompose for remote sensing images classification. IEEE Transactions on Circuits and Systems for Video Technology, 2025, 35(1): 3−18 doi: 10.1109/TCSVT.2022.3227172
[5]	Li X, Zhao C, Hu Y, Xie H, Wang Y, Zhao J. Precursor of privacy leakage detection for individual user. Computers & Security, 2024, 142: Article No. 103879
[6]	Chen C L P, Liu Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 10−24 doi: 10.1109/TNNLS.2017.2716952
[7]	Wang Z, Jusup M, Shi L, Lee J H, Iwasa Y, Boccaletti S. Exploiting a cognitive bias promotes cooperation in social dilemma experiments. Nature Communications, 2018, 9(1): Article No. 2954 doi: 10.1038/s41467-018-05259-5
[8]	Wu S, Wang J, Sun H, Zhang K, Pal N R. Fractional approximation of broad learning system. IEEE Transactions on Cybernetics, 2024, 54(2): 811−824 doi: 10.1109/TCYB.2021.3127152
[9]	赵慧敏, 郑建杰, 郭晨, 邓武. 基于流形正则化框架和MMD的域自适应BLS模型. 自动化学报, 2024, 50(7): 1458−1471 Zhao Hui-Min, Zheng Jian-Jie, Guo Chen, Deng Wu. Domain adaptive BLS model based on manifold regularization framework and MMD. Acta Automatica Sinica, 2024, 50(7): 1458−1471
[10]	Duan J, Yao S, Tan J, Liu Y, Chen L, Zhang Z, et al. Extreme fuzzy broad learning system: Algorithm, frequency principle, and applications in classification and regression. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(2): 2946−2957 doi: 10.1109/TNNLS.2023.3347888
[11]	Wang Z, Jusup M, Wang R W, Shi L, Iwasa Y, Moreno Y, et al. Onymitypromotes cooperation in social dilemma experiments. Science Advances, 2017, 3(3): Article No. e1601444 doi: 10.1126/sciadv.1601444
[12]	Liu L, Liu T, Chen C L P, Wang Y. Modal-regression-based broad learning system for robust regression and classification. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(9): 12344−12357 doi: 10.1109/TNNLS.2023.3256999
[13]	Shi M, Ding C, Wang R, Shen C, Huang W, Zhu Z. Semi-supervised class incremental broad network for continuous diagnosis of rotating machinery faults with limited labeled samples. Knowledge-Based Systems, 2024, 286: Article No. 111397 doi: 10.1016/j.knosys.2024.111397
[14]	Wang Z, Jusup M, Guo H, Shi L, Gecek S, Anand M, et al. Communicating sentiment and outlook reverses inaction against collective risks. Proceedings of the National Academy of Sciences of the United States of America, 2020, 117(30): 17650−17655 doi: 10.1073/pnas.1922345117
[15]	Jin J, Li Y, Chen C L P. Pattern classification with corrupted labeling via robust broad learning system. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(10): 4959−4971 doi: 10.1109/TKDE.2021.3049540
[16]	Jin J, Chang S, Duan J, Li Y, Ding W, Wang Z, et al. Groupwise label enhancement broad learning system for image classification. IEEE Transactions on Cybernetics, DOI: 10.1109/TCYB.2025.3550175
[17]	Wang Z, Mu C, Hu S, Chu C, Li X. Modelling the dynamics of regret minimization in large agent populations: A master equation approach. In: Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence. Vienna, Austria: Morgan Kaufmann, 2022. 534−540
[18]	Xiang S, Nie F, Meng G, Pan C, Zhang C. Discriminative least squares regression for multiclass classification and feature selection. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(11): 1738−1754 doi: 10.1109/TNNLS.2012.2212721
[19]	Jin J, Geng B, Li Y, Liang J, Xiao Y, Chen C L P. Flexible label-induced manifold broad learning system for multiclass recognition. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(11): 16076−16090 doi: 10.1109/TNNLS.2023.3291793
[20]	Rudin W. Principles of mathematical analysis. New York: McGraw-hill, 1976.
[21]	Zhang L, Yang M, Feng X, Ma Y, Zhang D. Collaborative representation based classification for face recognition. arXiv: 1204.2358, 2012.
[22]	Wang J, Yang J, Yu K, Lv F, Huang T, Gong Y. Locality-constrained linear coding for image classification. In: Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2010. 3360−3367
[23]	Naseem I, Togneri R, Bennamoun M. Linear regression for face recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(11): 2106−2112 doi: 10.1109/TPAMI.2010.128
[24]	Chen C, Wei C, Wang Y F. Low-rank matrix recovery with structural incoherence for robust face recognition. In: Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA: IEEE, 2012. 2618−2625
[25]	Zhang Y, Jiang Z, Davis L S. Learning structured low-rank representations for image classification. In: Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2013. 676−683
[26]	Julien M, Francis B, Jean P. Task-driven dictionary learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 791−804 doi: 10.1109/TPAMI.2011.156
[27]	Fang X, Xu Y, Li X, Lai Z, Wong W K, Fang B. Regularized label relaxation linear regression. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(4): 1006−1018 doi: 10.1109/TNNLS.2017.2648880
[28]	Candès E J, Li X, Ma Y, Wright J. Robust principal component analysis? Journal of the ACM (JACM), 2011, 58(3): 1−37
[29]	Liu G, Yan S. Latent low-rank representation for subspace segmentation and feature extraction. In: Proceedings of the 2011 International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011. 1615−1622
[30]	Cai X, Ding C, Nie F, Huang H. On the equivalent of low-rank linear regressions and linear discriminant analysis based regressions. In: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago, USA: ACM, 2013. 1124−1132
[31]	Wei C, Chen C, Wang Y. Robust face recognition with structurally incoherent low-rank matrix decomposition. IEEE Transactions on Image Processing, 2014, 23(8): 3294−3307 doi: 10.1109/TIP.2014.2329451
[32]	Li Y, Liu J, Lu H, Ma S. Learning robust face representation with classwise block-diagonal structure. IEEE Transactions on Information Forensics and Security, 2014, 9(12): 2051−2062 doi: 10.1109/TIFS.2014.2361936
[33]	Fernández-Delgado M, Cernadas E, Barro S, Amorim D. Do we need hundreds of classifiers to solve real world classification problems? The Journal of Machine Learning Research, 2014, 15(1): 3133−3181
[34]	Wen J, Deng S, Fei L, Zhang Z, Zhang B, Zhang Z, et al. Discriminative regression with adaptive graph diffusion. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(2): 1797−1809 doi: 10.1109/TNNLS.2022.3185408
[35]	Li X, Wei J, Jin J, Xu T, Yu D. Fisher regularized discriminative broad learning system for visual classification. Applied Soft Computing, 2024, 167: Article No. 112341 doi: 10.1016/j.asoc.2024.112341
[36]	Georghiades A S, Belhumeur P N, Kriegman D J. From few to many: Illumination cone models for face recognition under variable lighting and pose. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 643−660 doi: 10.1109/34.927464
[37]	Jiang Z, Lin Z, Davis L S. Label consistent K-SVD: Learning a discriminative dictionary for recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2651−2664 doi: 10.1109/TPAMI.2013.88
[38]	Mohan B C, Chaitanya T K, Tirupal T. Fast and accurate content based image classification and retrieval using gaussian hermite moments applied to coil 20 and coil 100. In: Proceedings of the 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT). Kanpur, India: IEEE, 2019: 1−5