-
摘要: 离线强化学习领域面临的核心挑战在于如何避免分布偏移并限制值函数的过估计问题. 尽管传统的TD3+BC算法通过引入行为克隆正则项, 有效地约束了习得策略, 使其更接近行为策略, 从而在一定程度上得到了有竞争力的性能, 但其策略稳定性在训练过程中仍有待提高. 尤其在现实世界中, 策略验证可能涉及高昂的成本, 因此提高策略稳定性尤为关键. 本研究受到深度学习中“平坦最小值”概念的启发, 旨在探索目标策略损失函数在动作空间中的平坦区域, 以得到稳定策略. 为此, 提出了一种梯度损失函数(Gradient Loss Function, GLF), 并基于此设计了一种新的离线强化学习算法—梯度损失离线强化学习算法 (Gradient Loss for Offline Reinforcement Learning, GLO). 在D4RL基准数据集上的实验结果表明, GLO算法在性能上超越了当前的主流算法. 此外, 还尝试将本研究的方法扩展到在线强化学习领域, 实验结果证明了该方法在在线强化学习环境下 的普适性和有效性.Abstract: Offline Reinforcement Learning faces the challenges of preventing distributional shifts and avoiding the overestimation of value functions. While the traditional TD3+BC algorithm achieves competitive performance by introducing behavioral cloning regularization to constrain the learned policy to be closer to the behavior policy, its policy stability during training still needs improvement. Especially in the real world, policy validation can be costly, making policy stability crucial. Inspired by the concept of “flat minima” in deep learning, this study aims to explore the flat regions of the target policy loss function in the action space to obtain a stable policy. To achieve this, a Gradient Loss Function (GLF) is proposed, and a new offline reinforcement learning algorithm called Gradient Loss for Offline Reinforcement Learning (GLO) is designed. Experimental results on the D4RL benchmark dataset show that the GLO algorithm outperforms current mainstream algorithms. Furthermore, we extend our approach to the online reinforcement learning domain, demonstrating its generalizability and effectiveness in online reinforcement learning environments.
-
图 1 hopper-medium环境下的标准化奖励分布直方图
Fig. 1 Histogram of normalized reward distribution for hopper-medium environment
表 1 实验中的超参数设置
Table 1 Hyperparameters in the experiment
超参数名称 值 描述 $ \gamma $ 0.99 折扣因子 max_timesteps 1e6 训练轮数 policy_freq 2 每过几轮更新策略 Q函数网络 FC(256,256,256) 全连接层(Fully connected layers,
FC), 加入标准化层,
激活函数为ReLUBC网络、残差
策略网络FC(256,256,256) 全连接层, 激活函数为ReLU 学习率 0.001 策略网络和Q函数网络学习率 优化器 Adam 策略网络和Q函数网络优化器 $ \tau _ q$ 见表2 Q函数网络更新系数 $ \tau _ {action}$ 见表2 策略网络更新系数 $ \lambda$ 见表2 梯度损失函数中梯度的系数 
下载: 导出CSV
表 2 实验中更新系数$ \tau $的设置
Table 2 Update rate $ \tau $ settings in the experiment
环境 $ \tau _ q$ $ \tau _ {\text{action}}$ $ \lambda$ halfcheetah-m 5e-3 5e-3 1.5e-1 halfcheetah-m-r 2e-3 1e-5 5e-2 halfcheetah-m-e 1e-3 1e-5 5e-3 walker2d-m 2e-3 1e-6 1e-1 walker2d-m-r 4e-4 1e-6 3e-2 walker2d-m-e 2e-3 2e-3 4e-2 hopper-m 2e-3 5e-7 5e-2 hopper-m-r 1e-3 1e-3 2e-2 hopper-m-e 2e-3 1e-5 1e-2 antmaze-umaze 2e-3 2e-3 1e-3 antmaze-umaze-diverse 5e-3 5e-3 1e1
下载: 导出CSV
表 3 GLO和主流算法得到的标准化奖励
Table 3 Normalized rewards achieved by GLO and mainstream algorithms
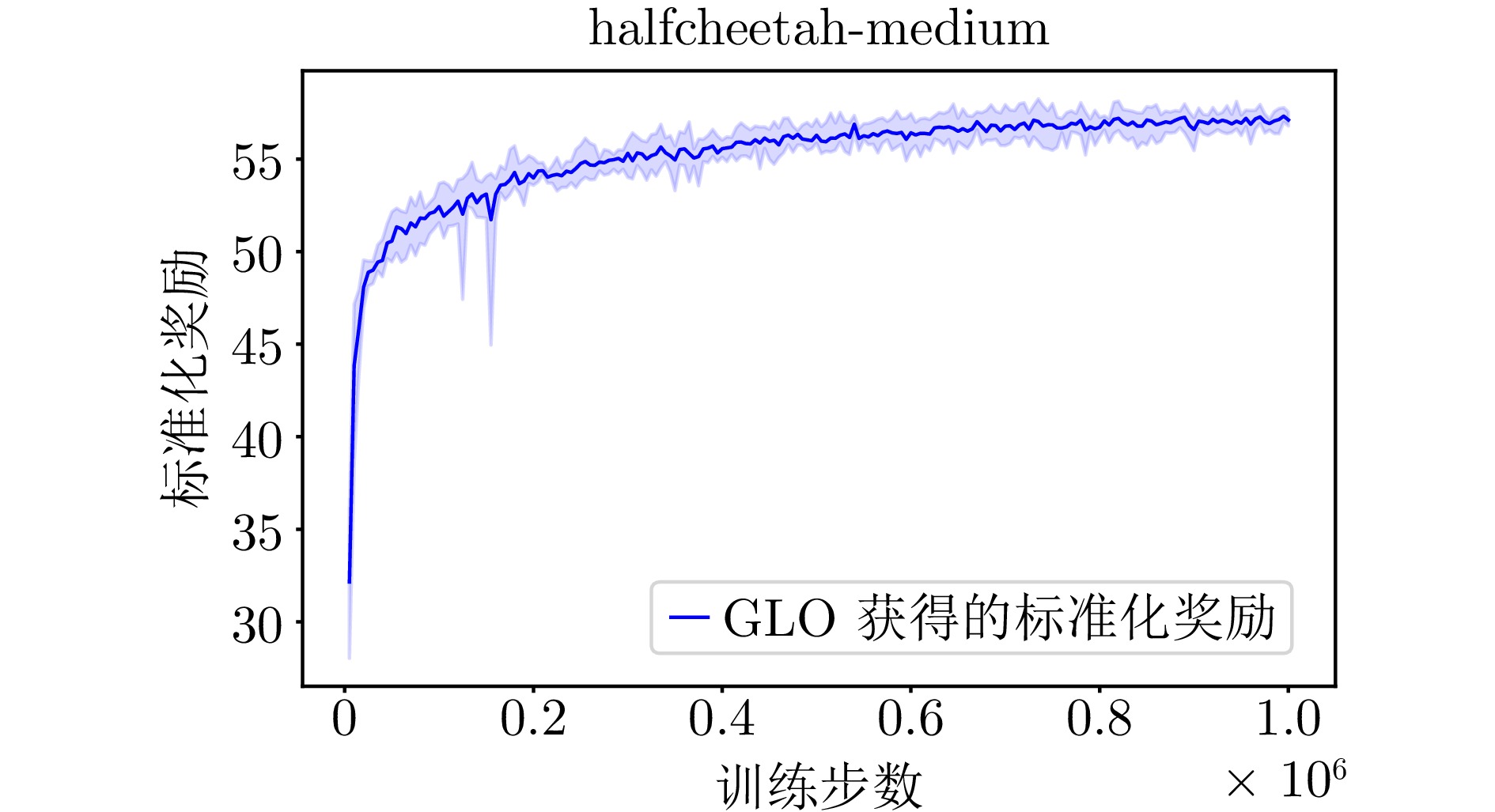
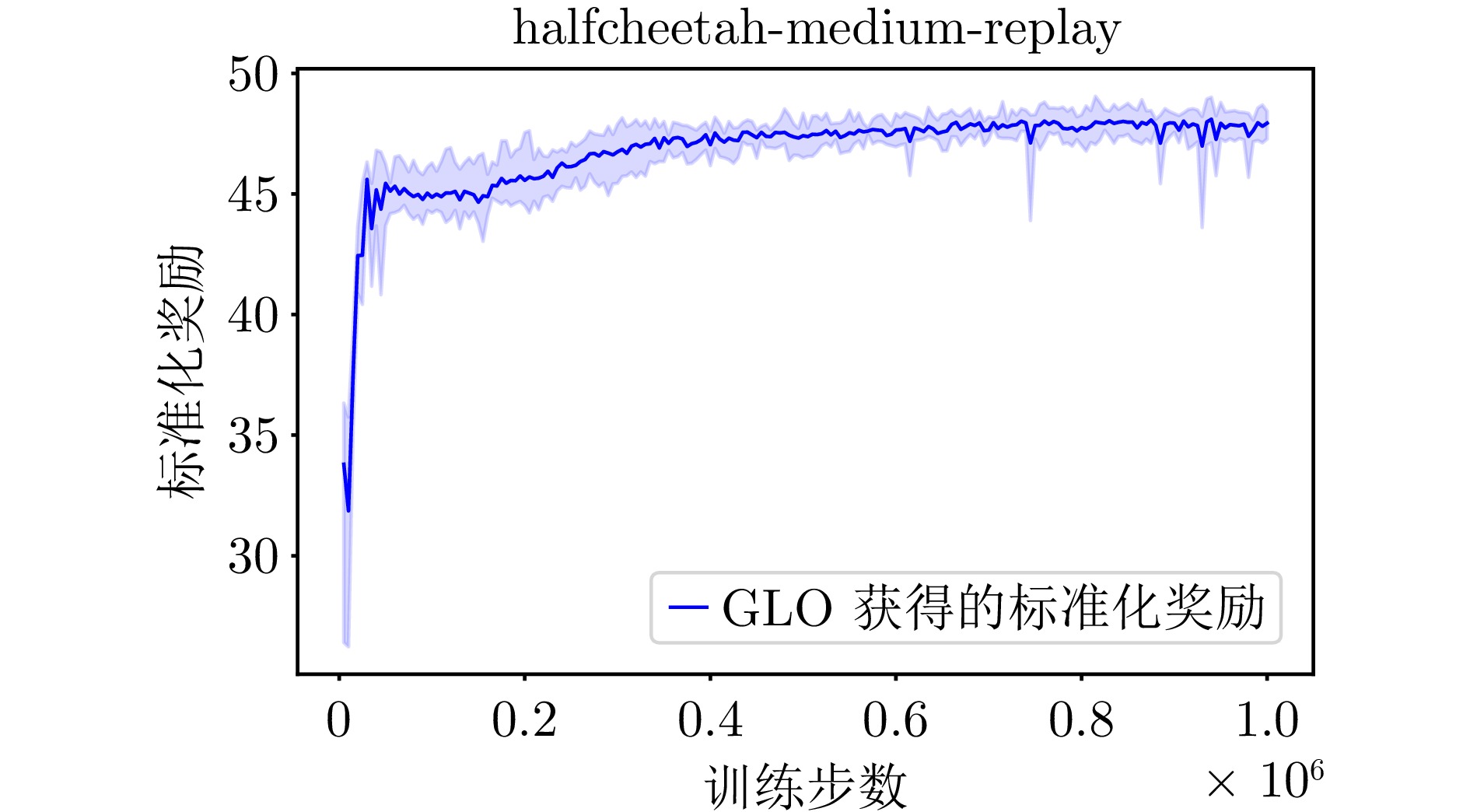
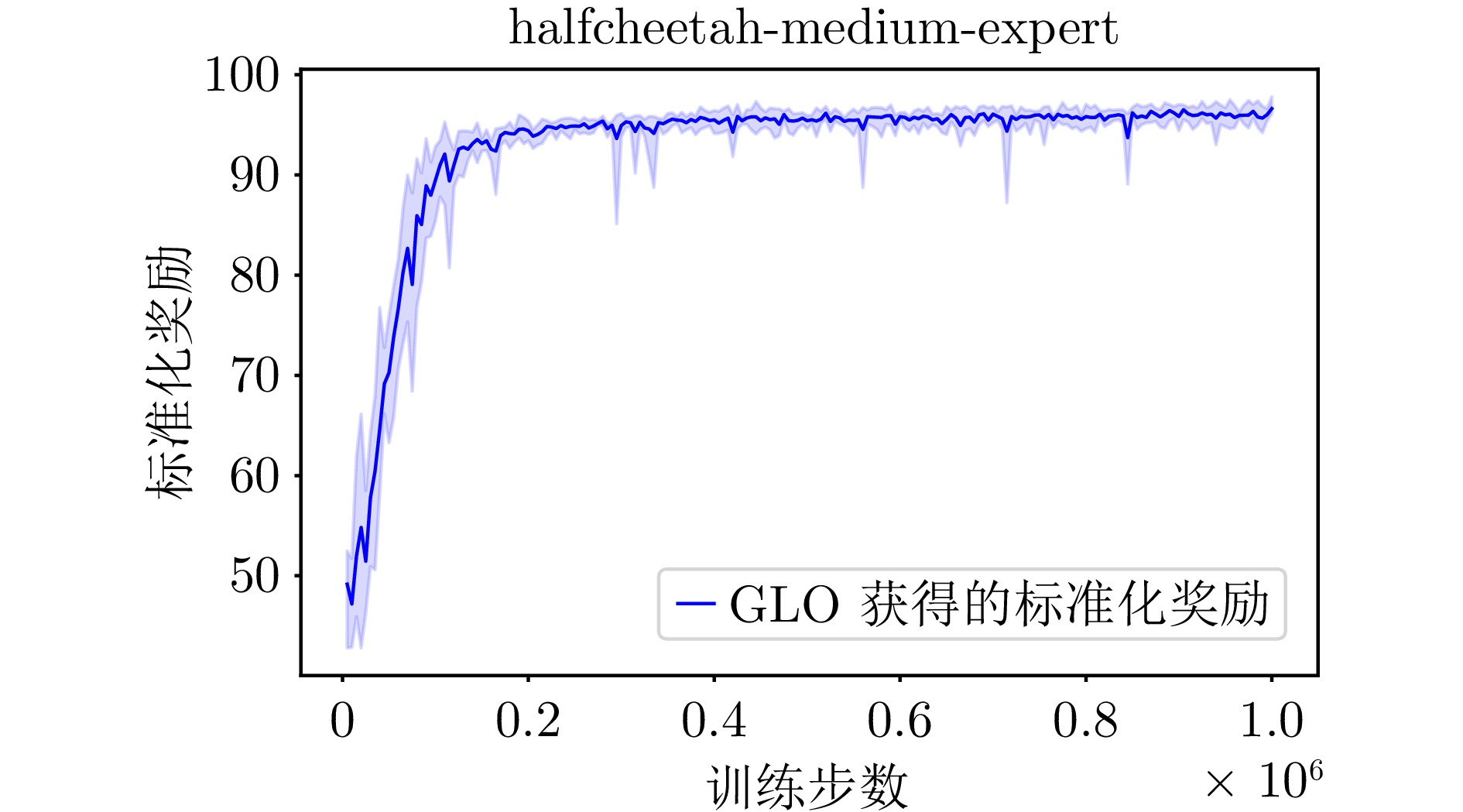
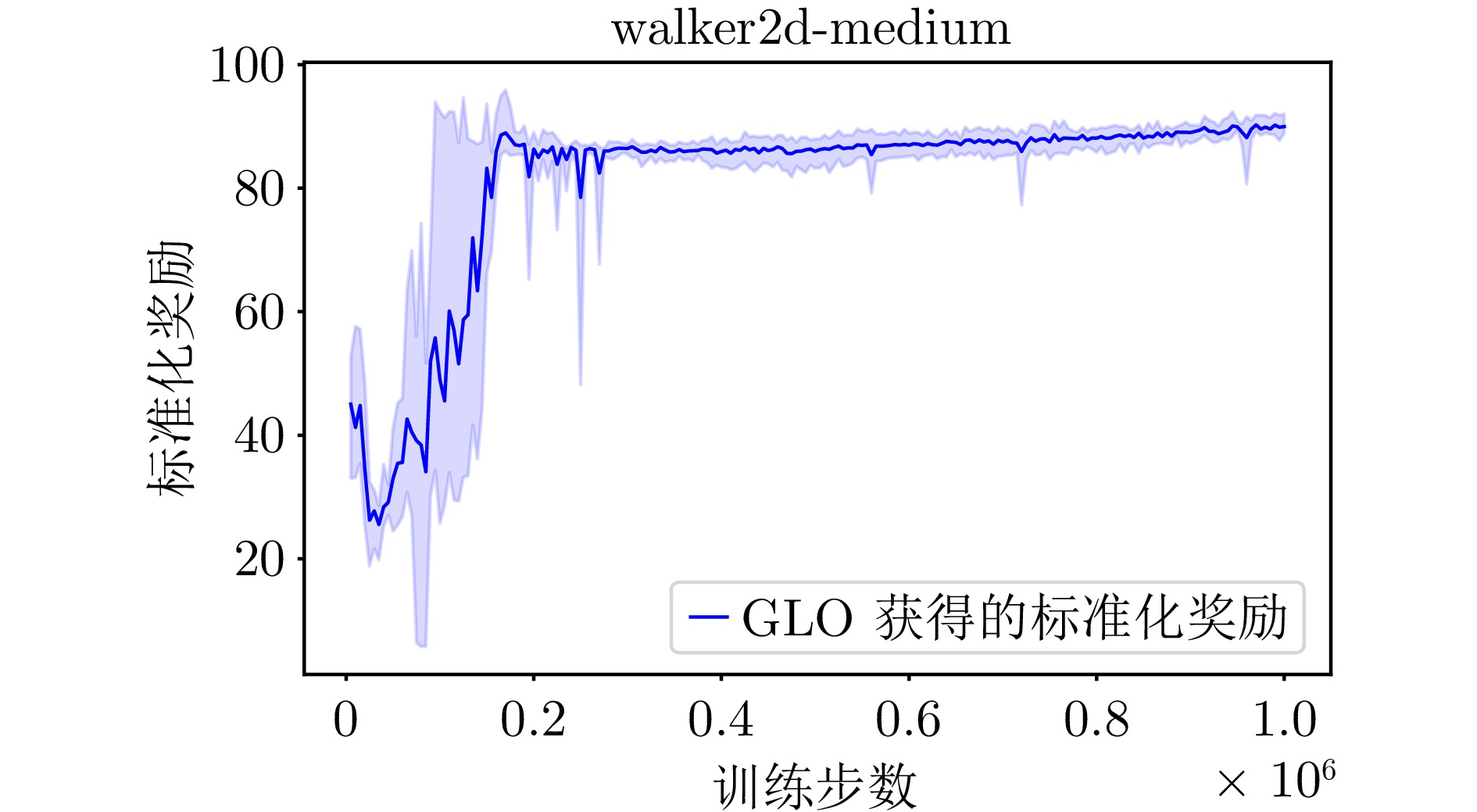
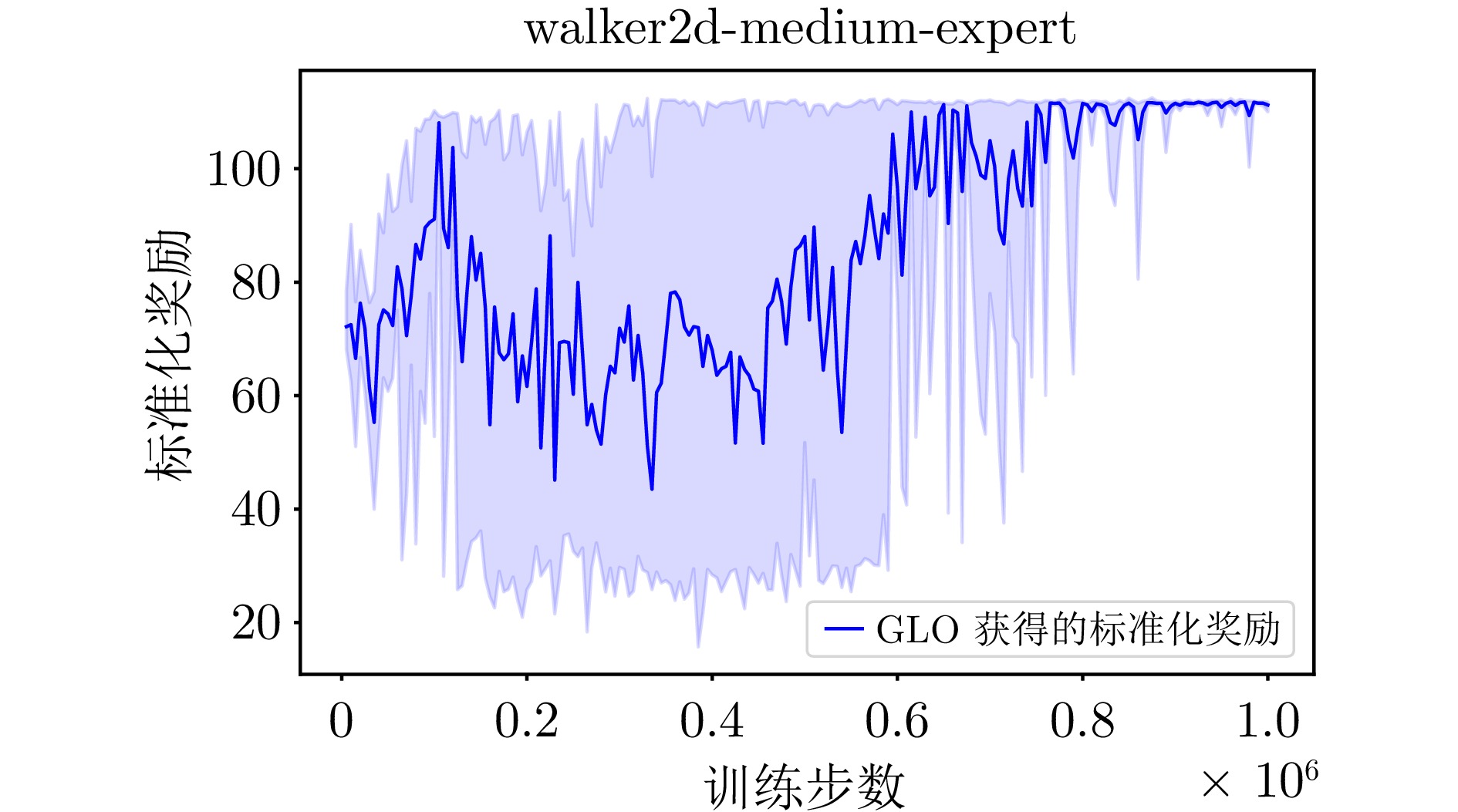
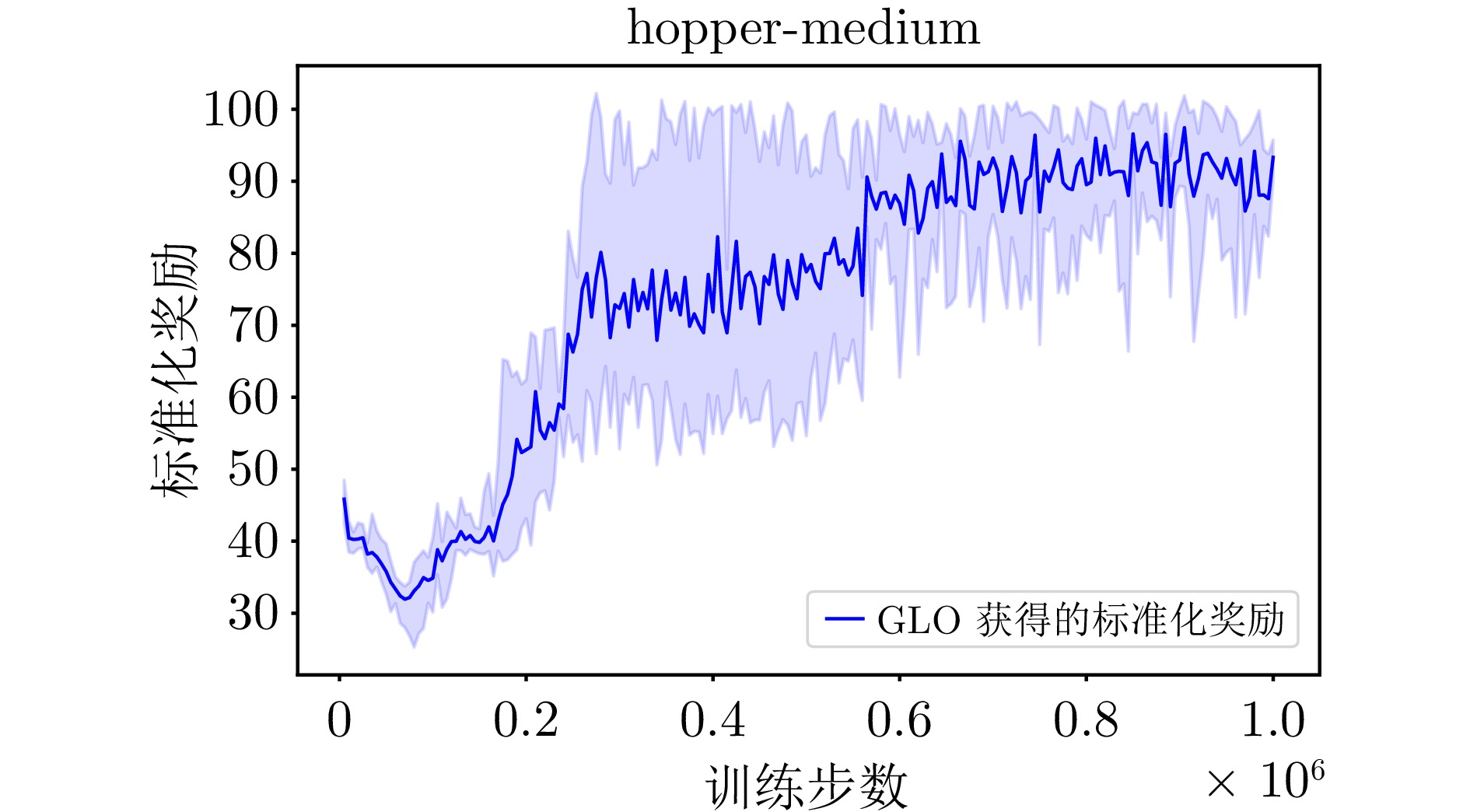
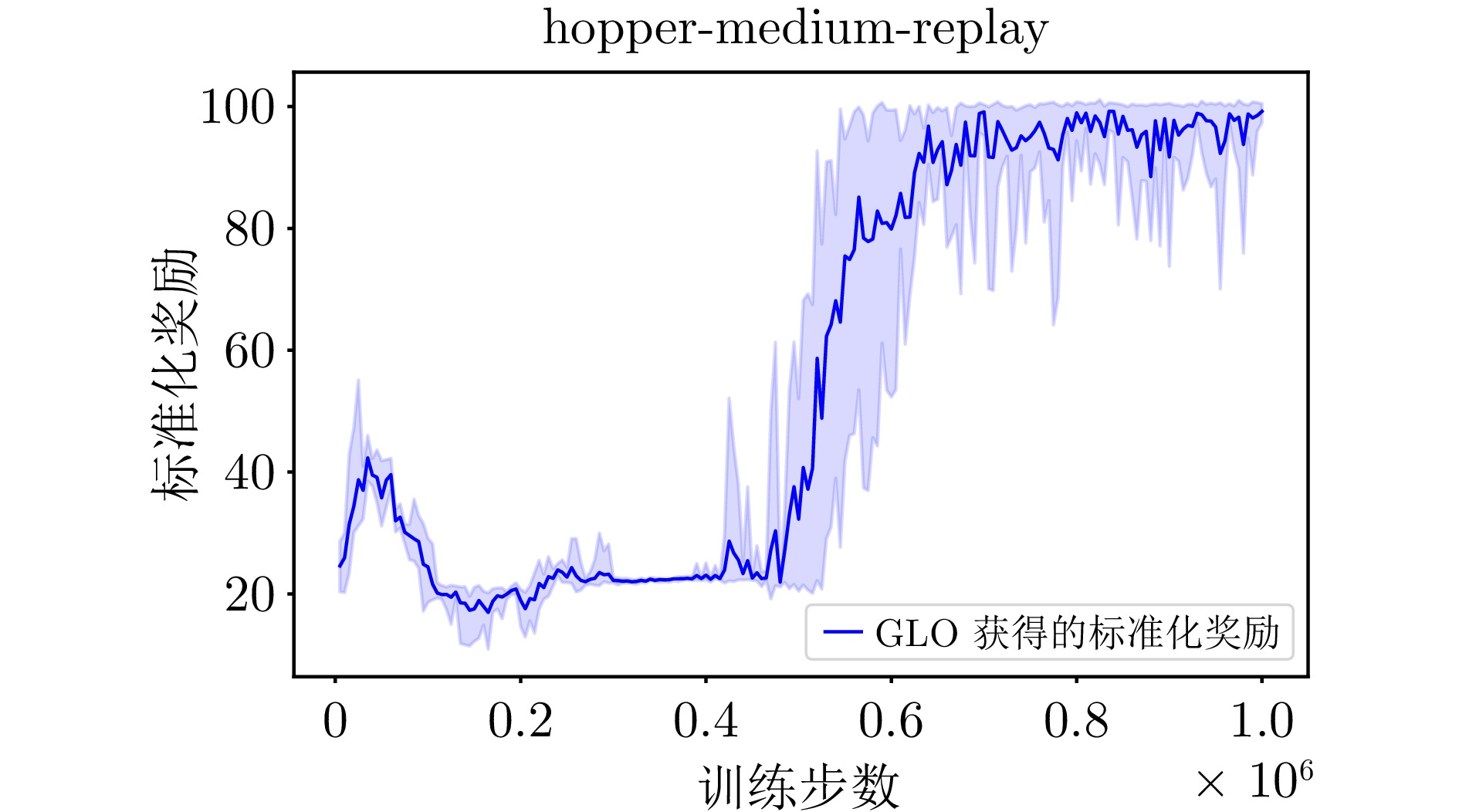
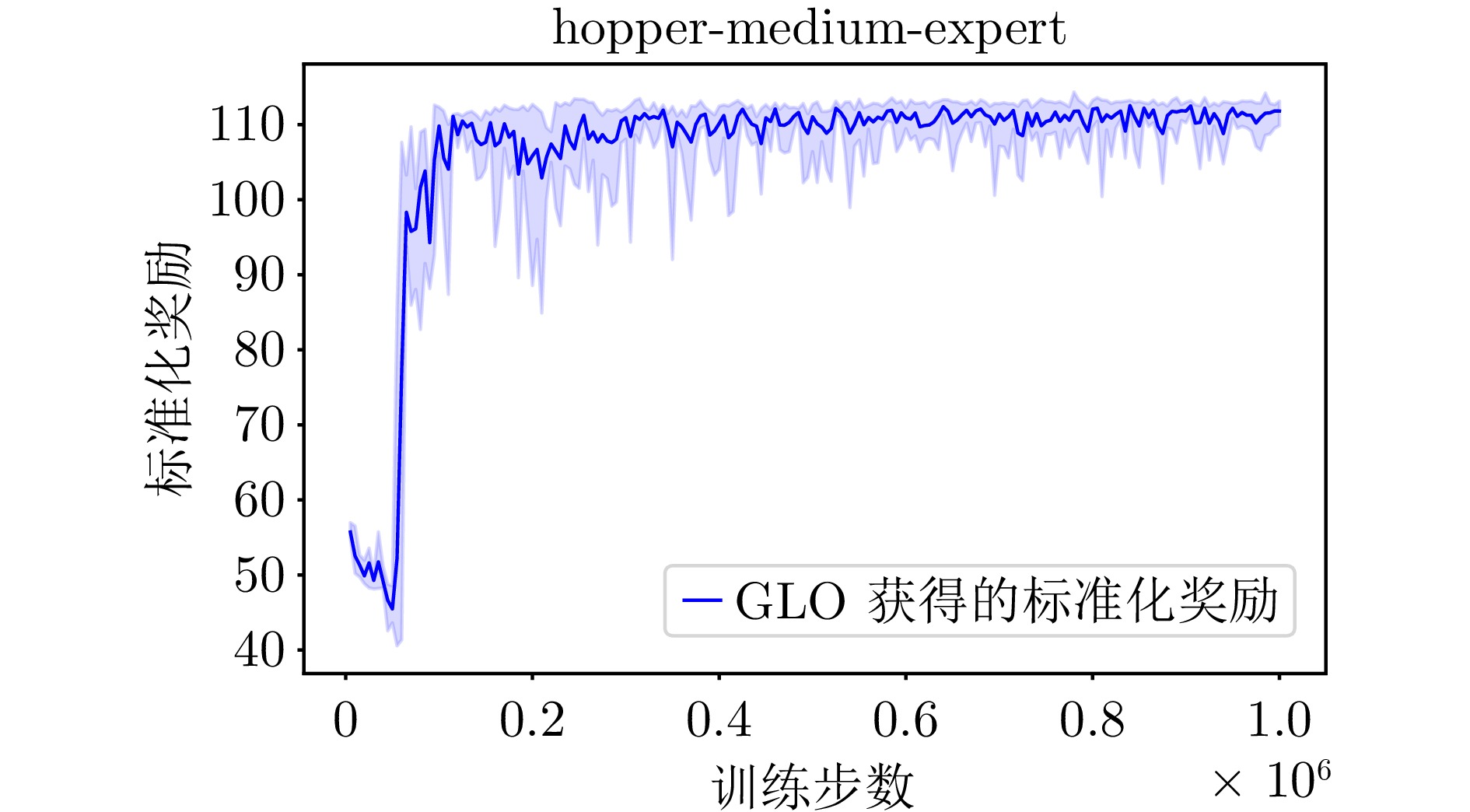
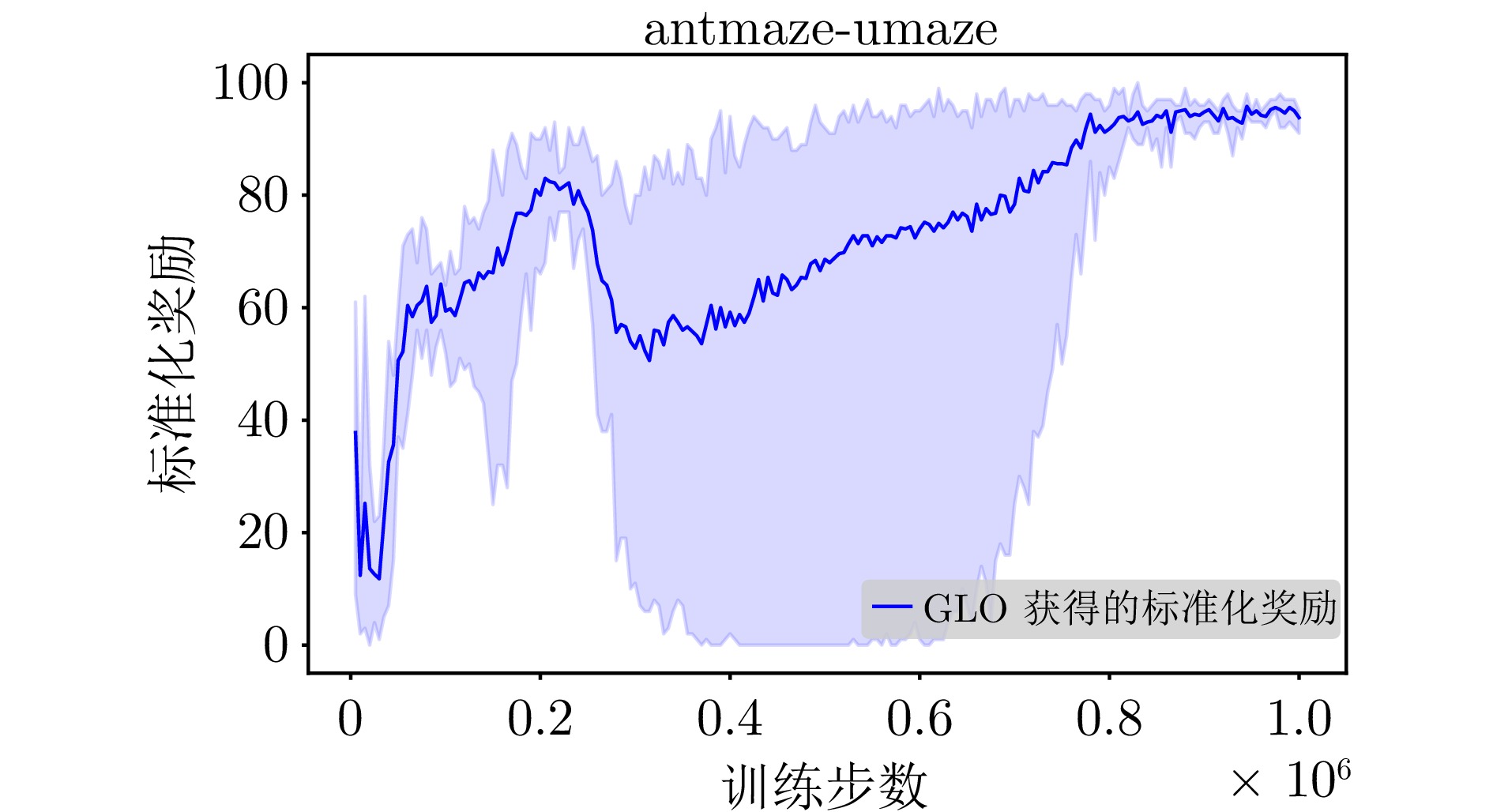
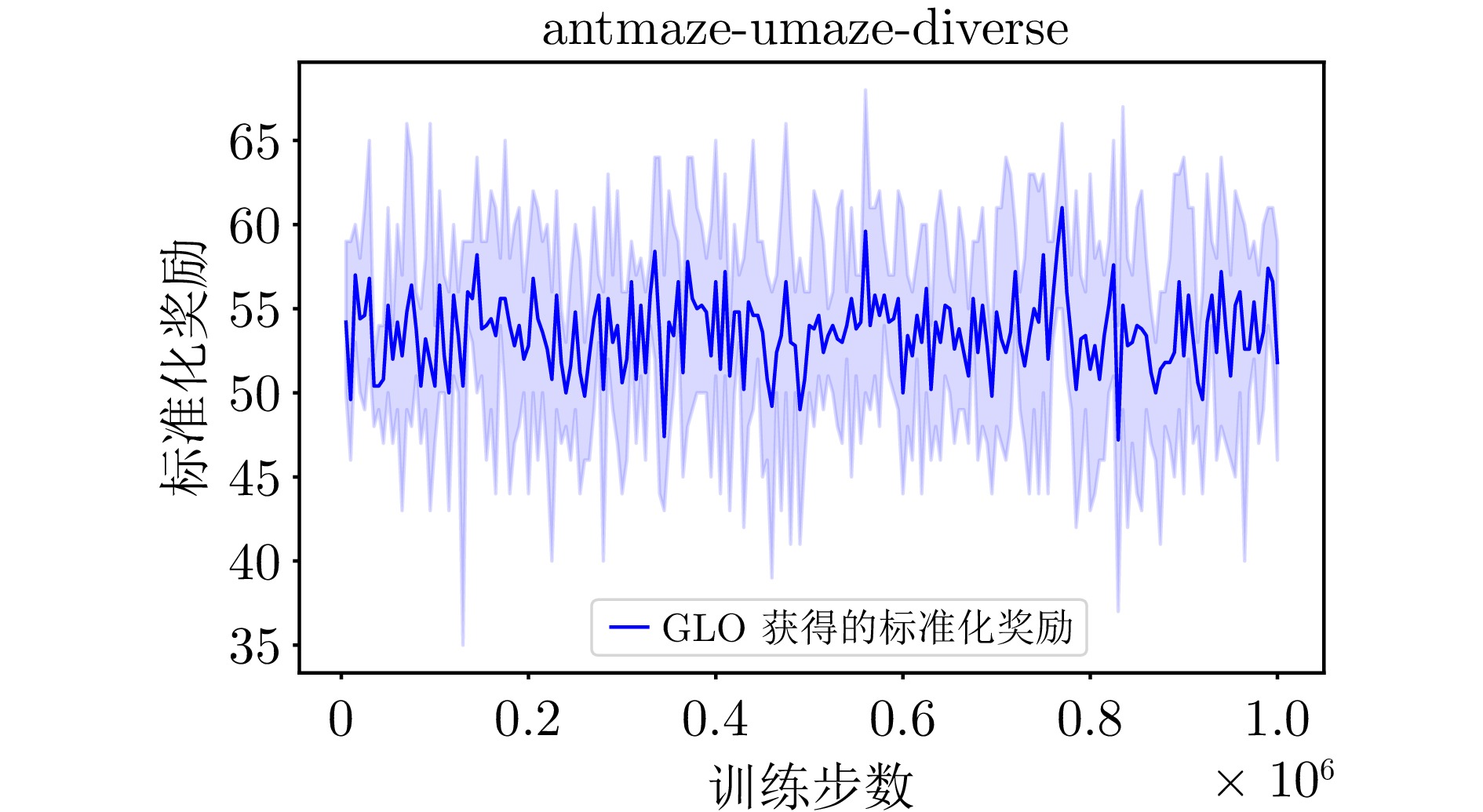
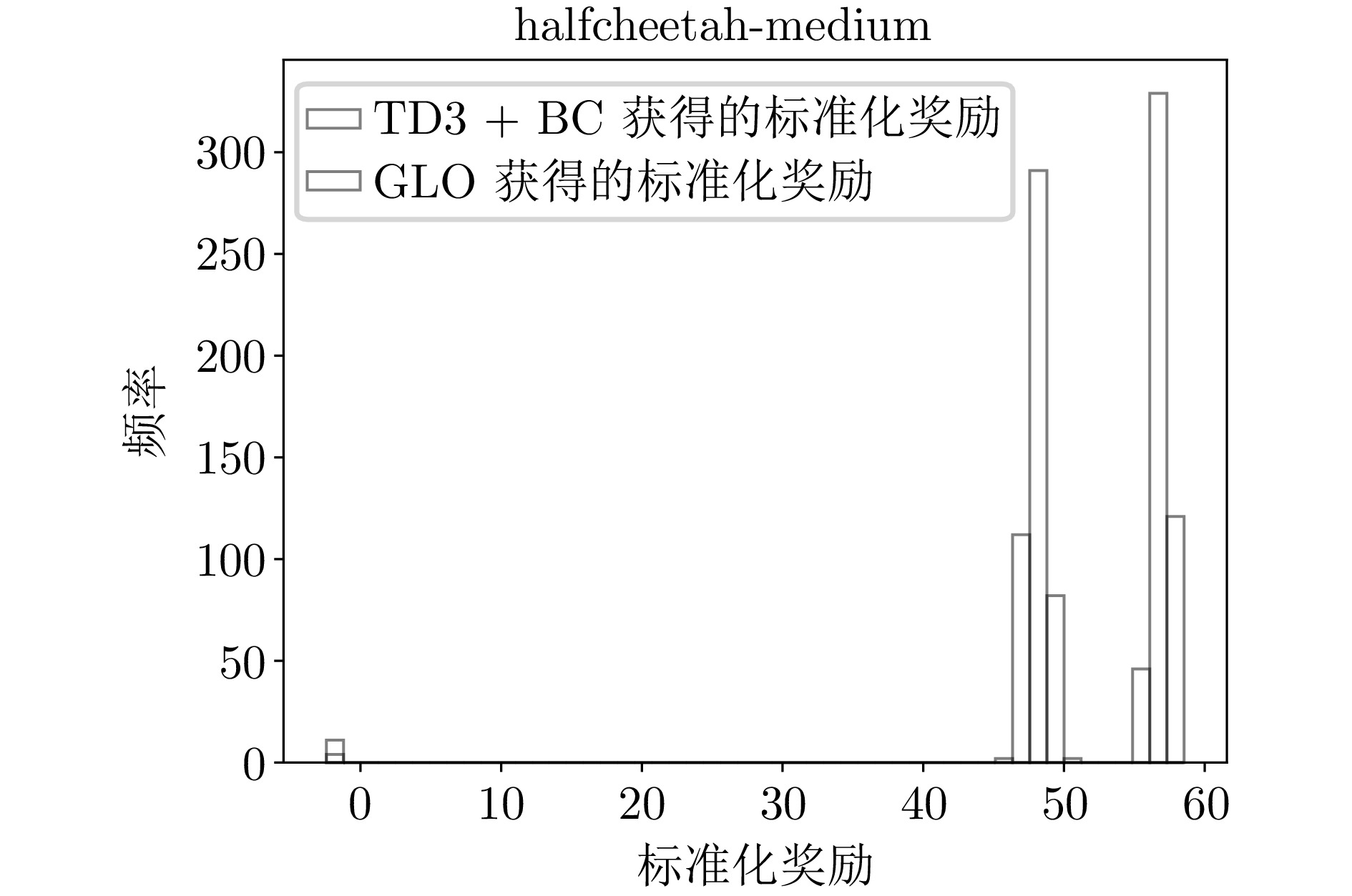
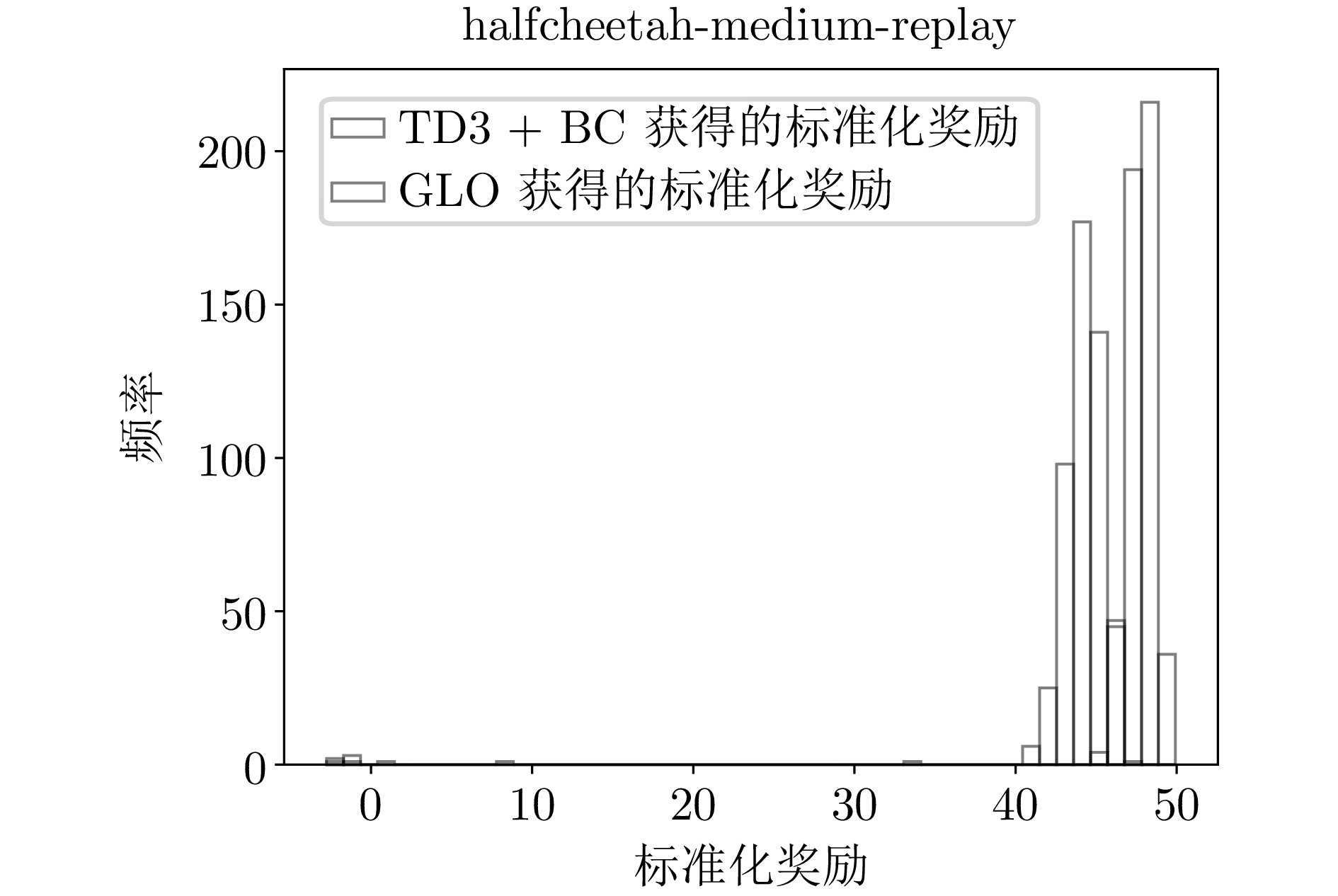
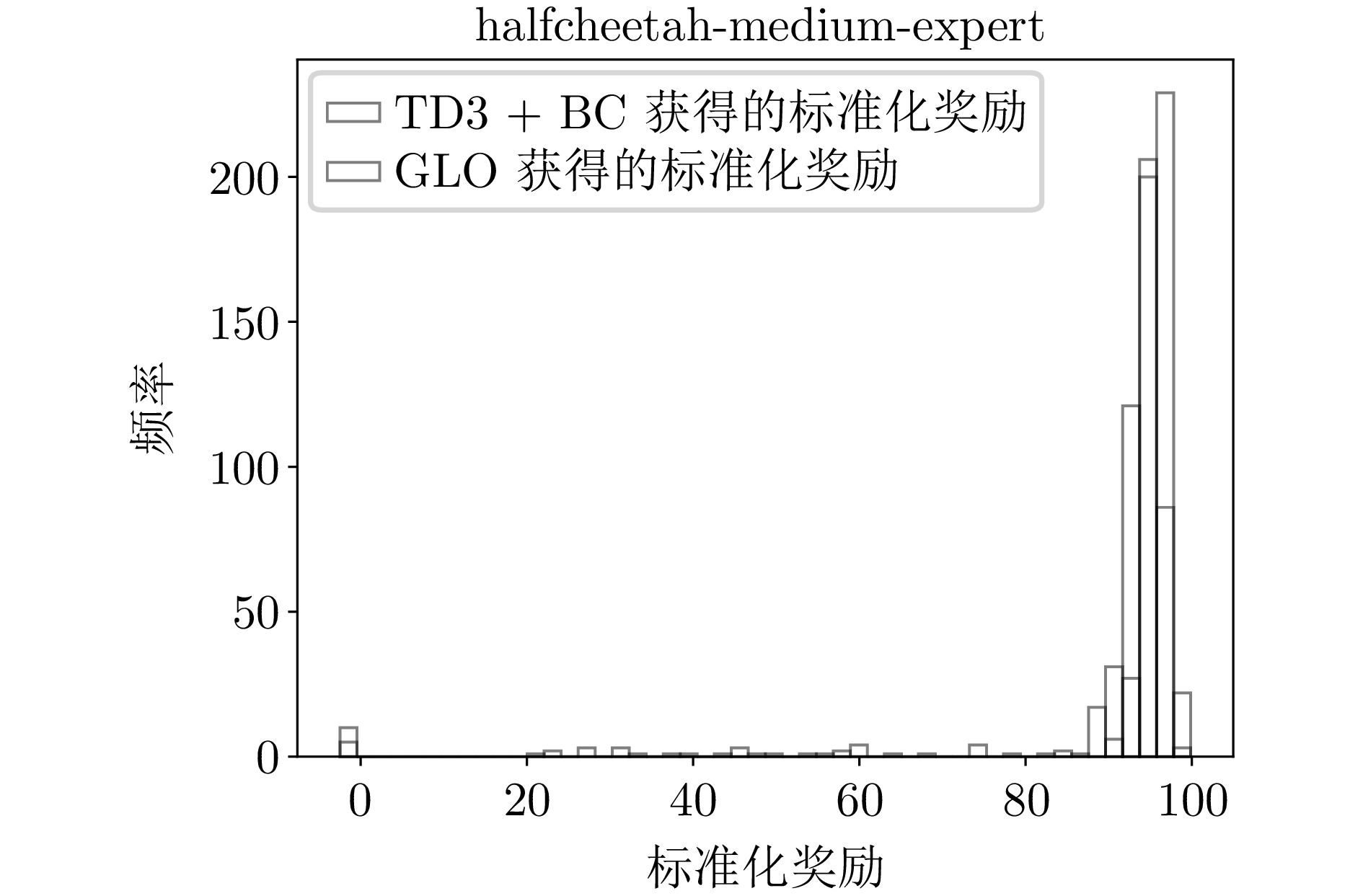
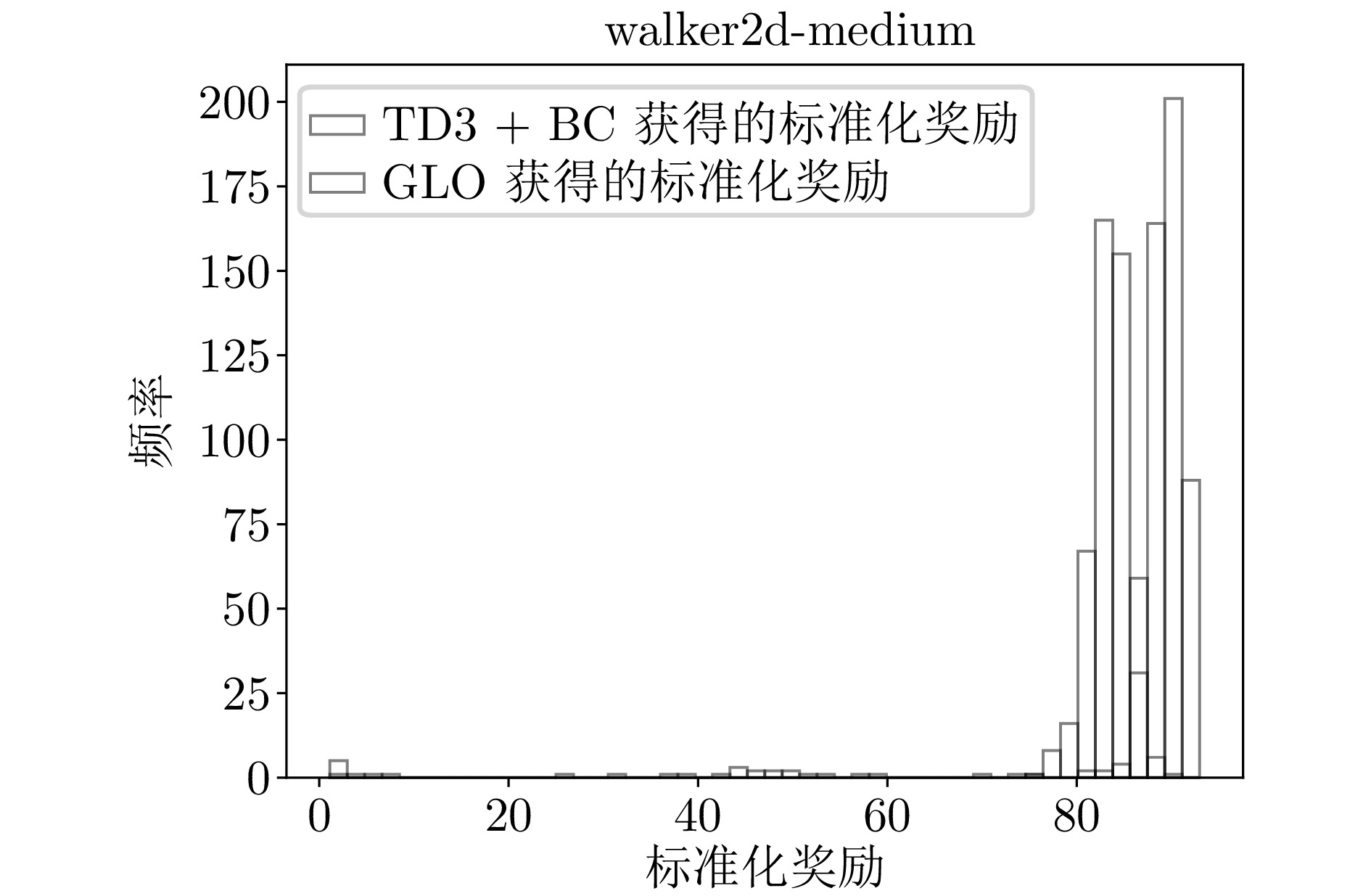
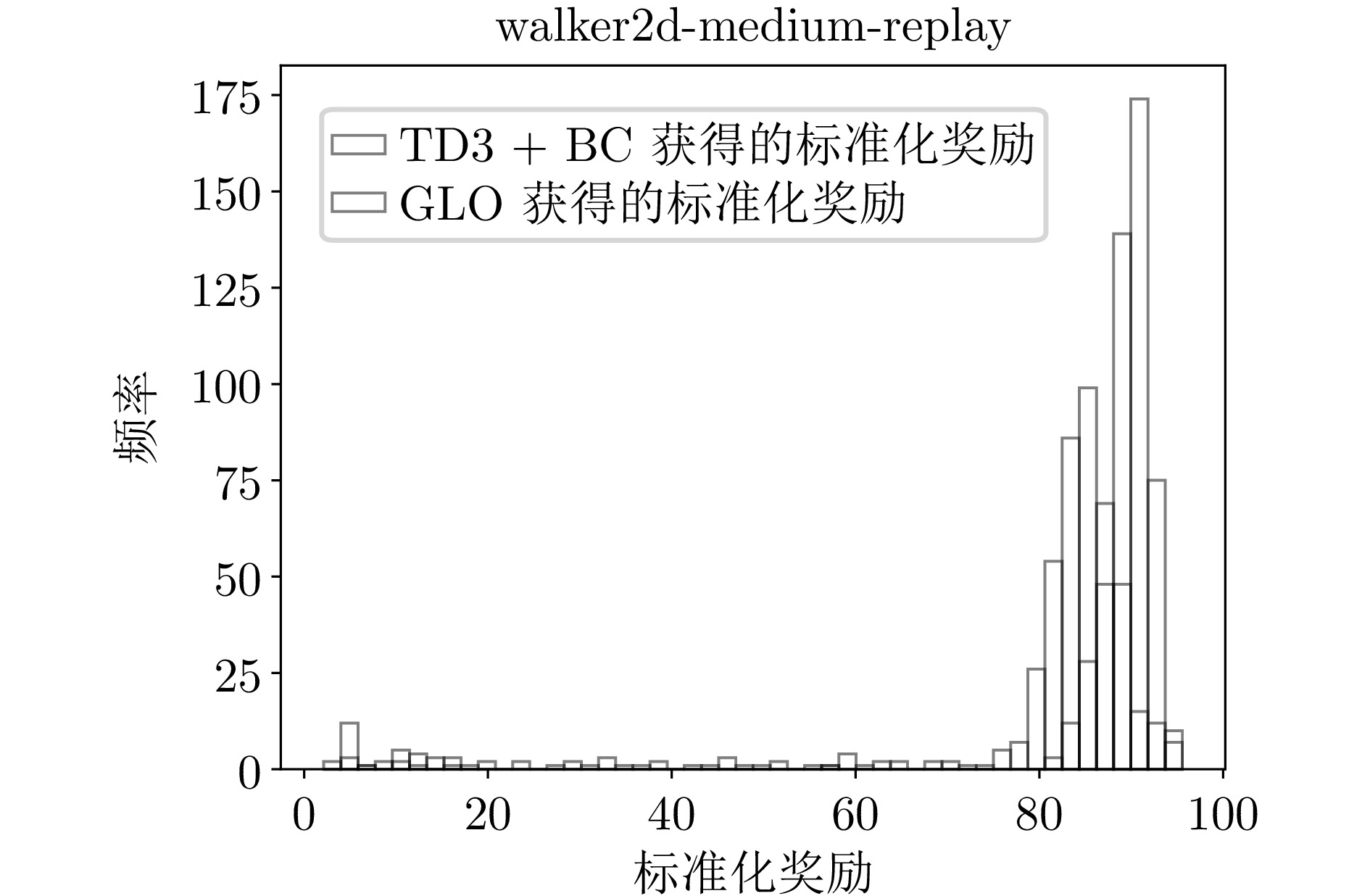
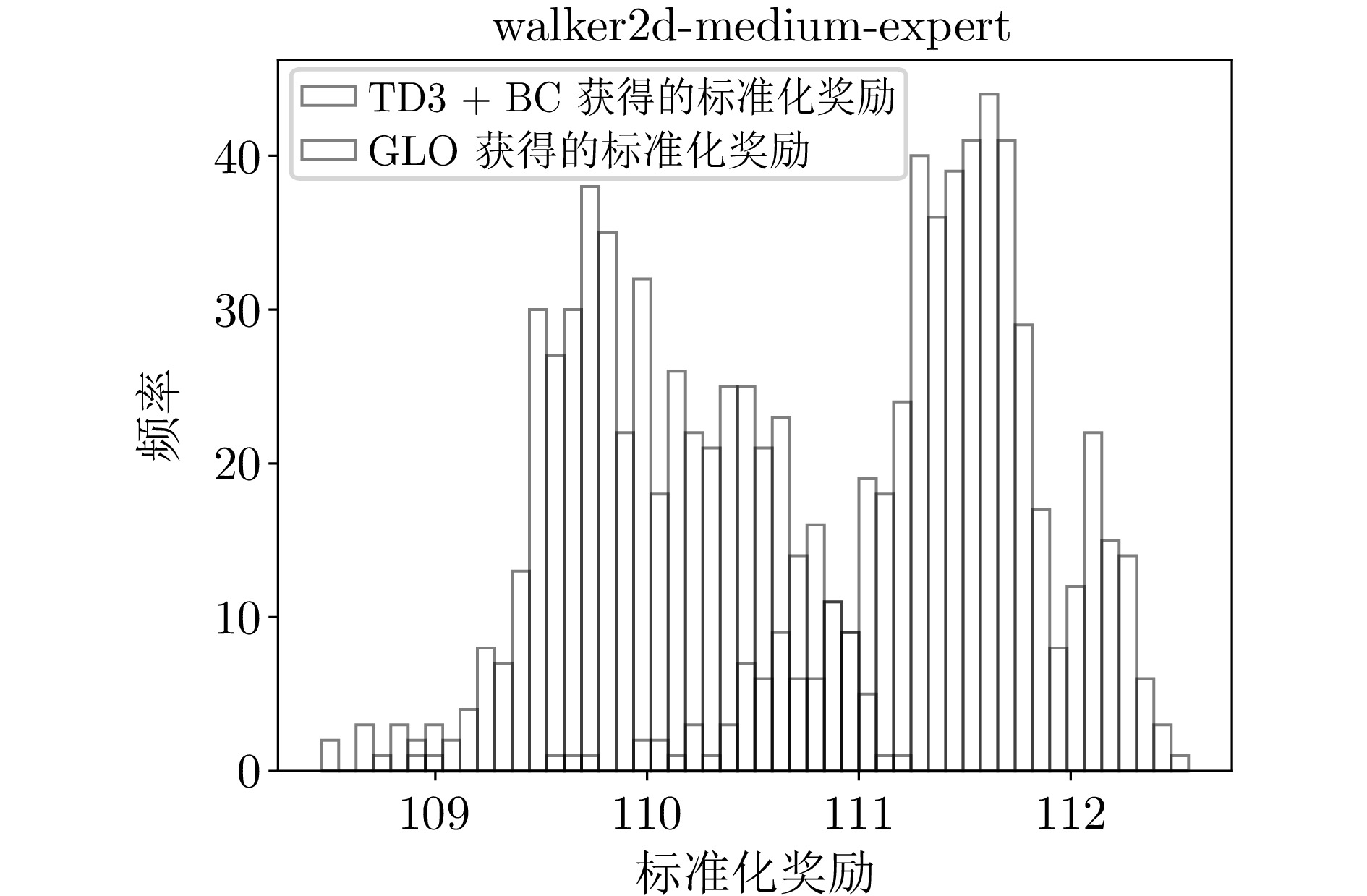
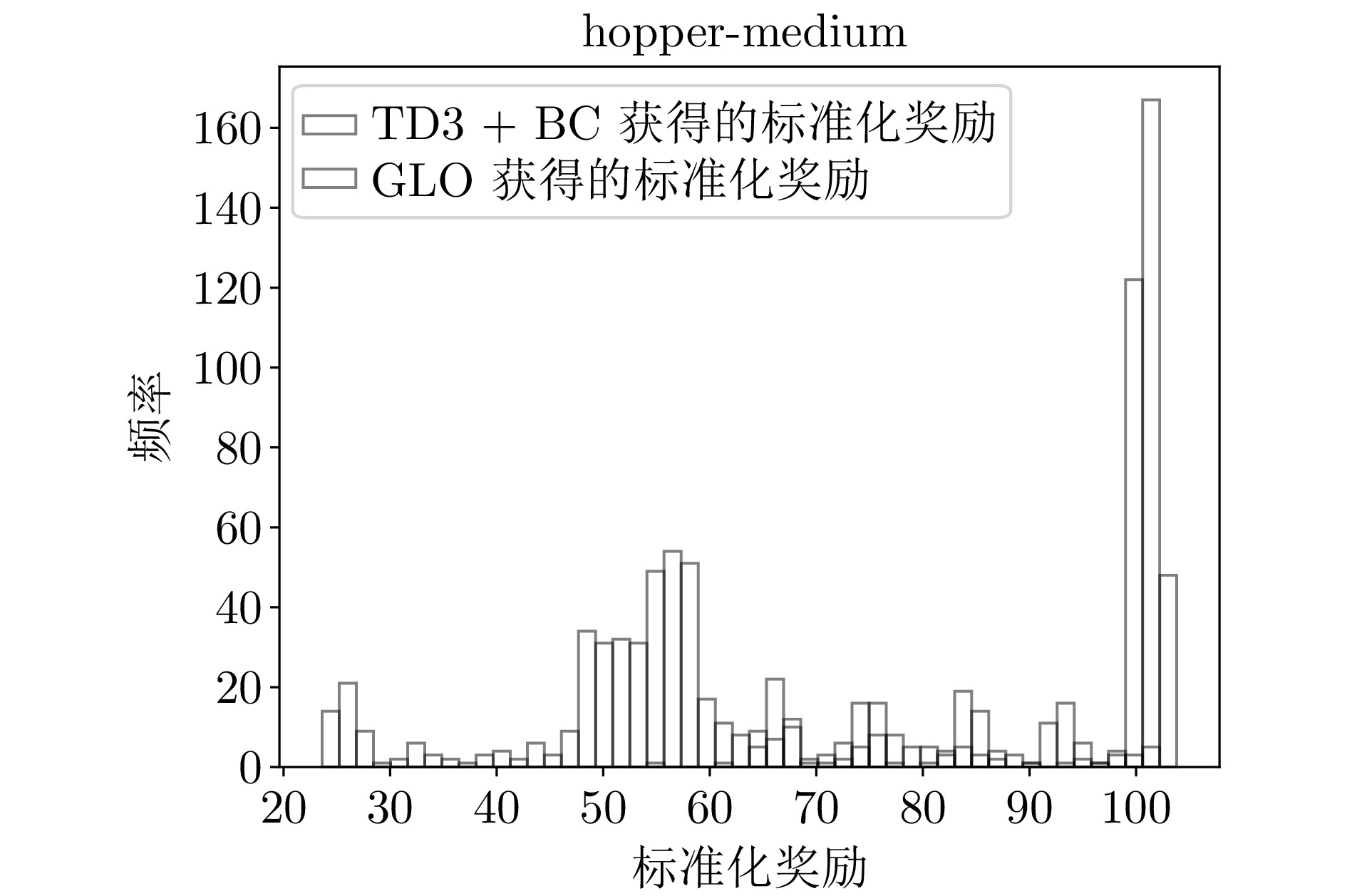
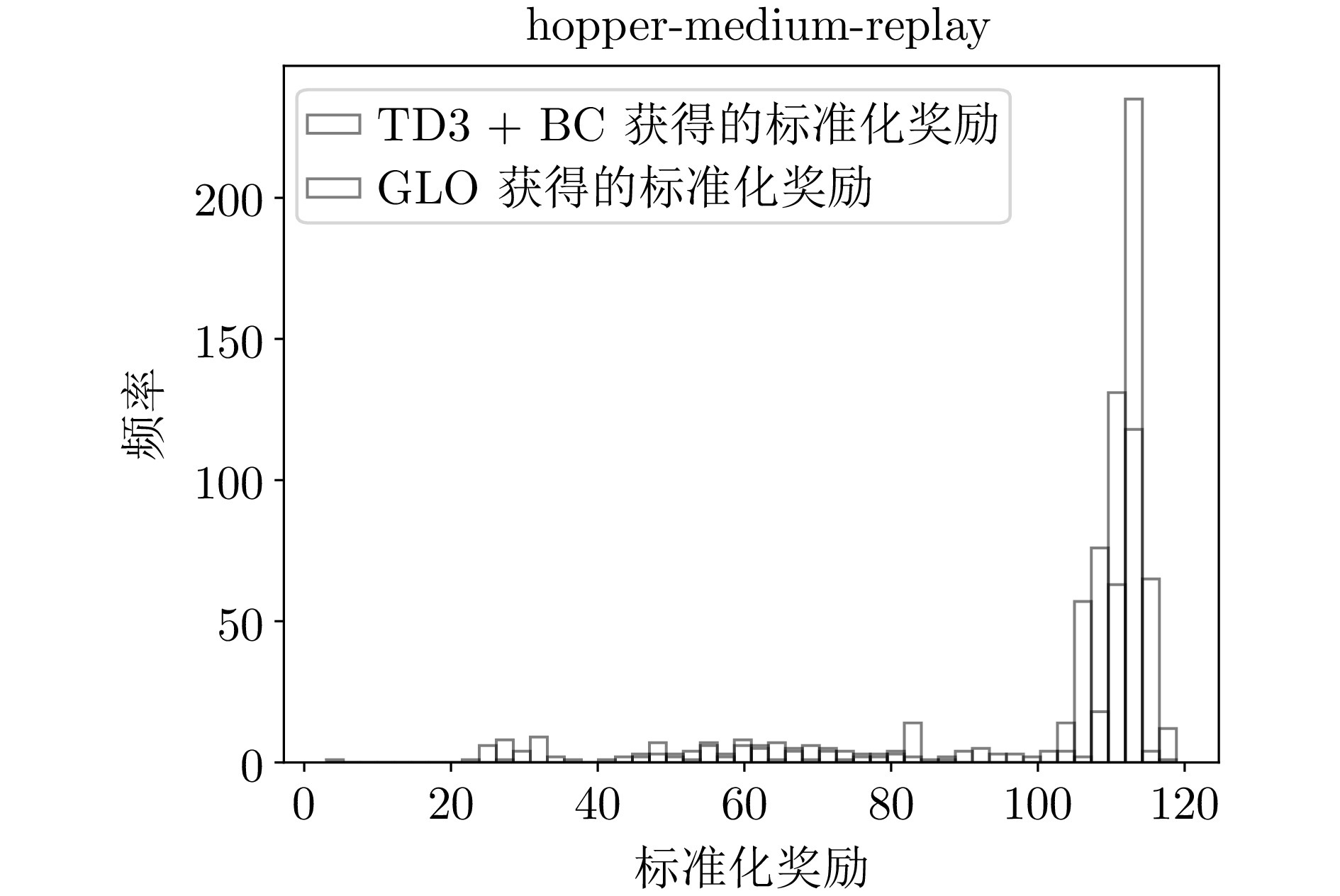
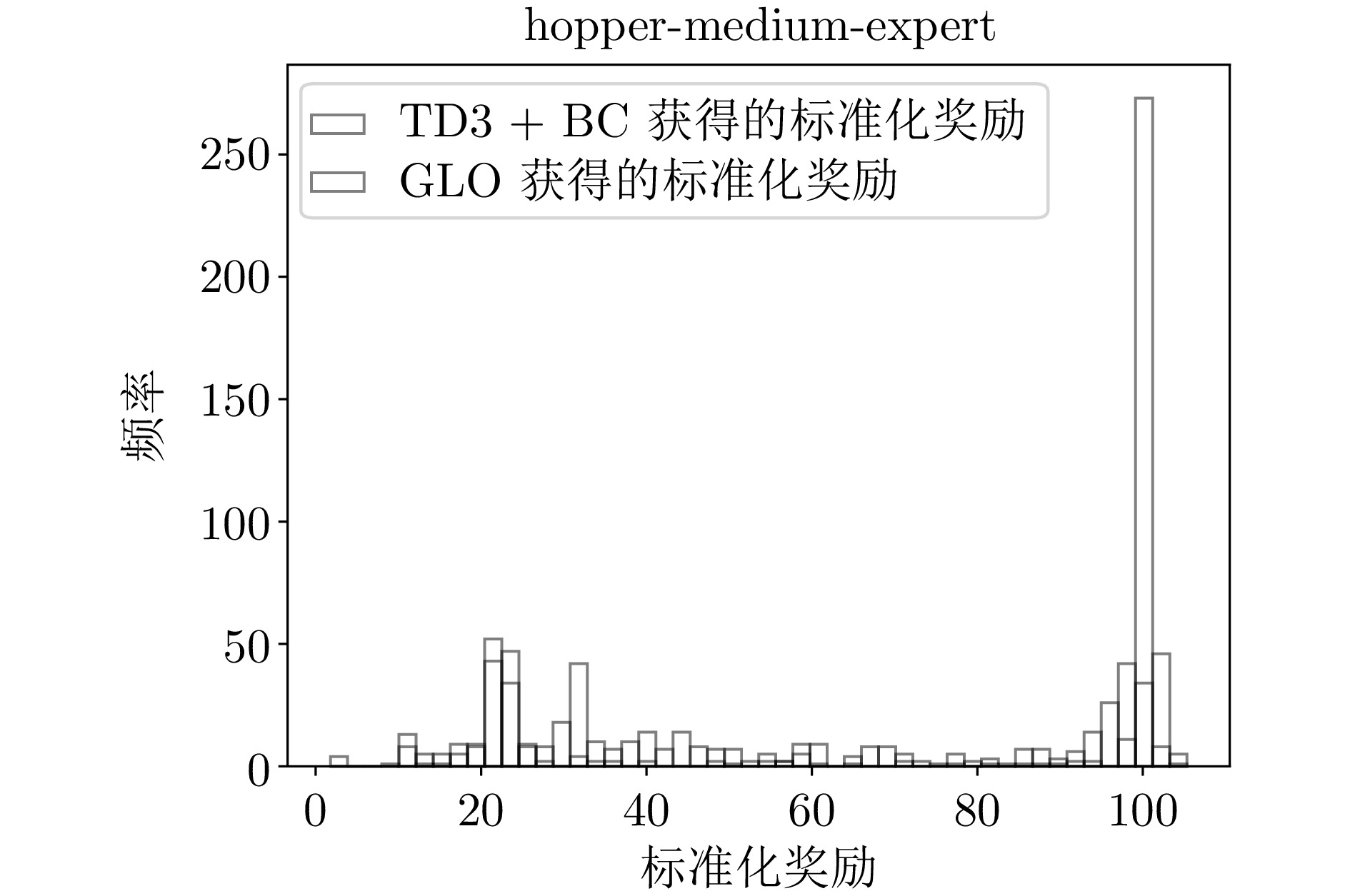
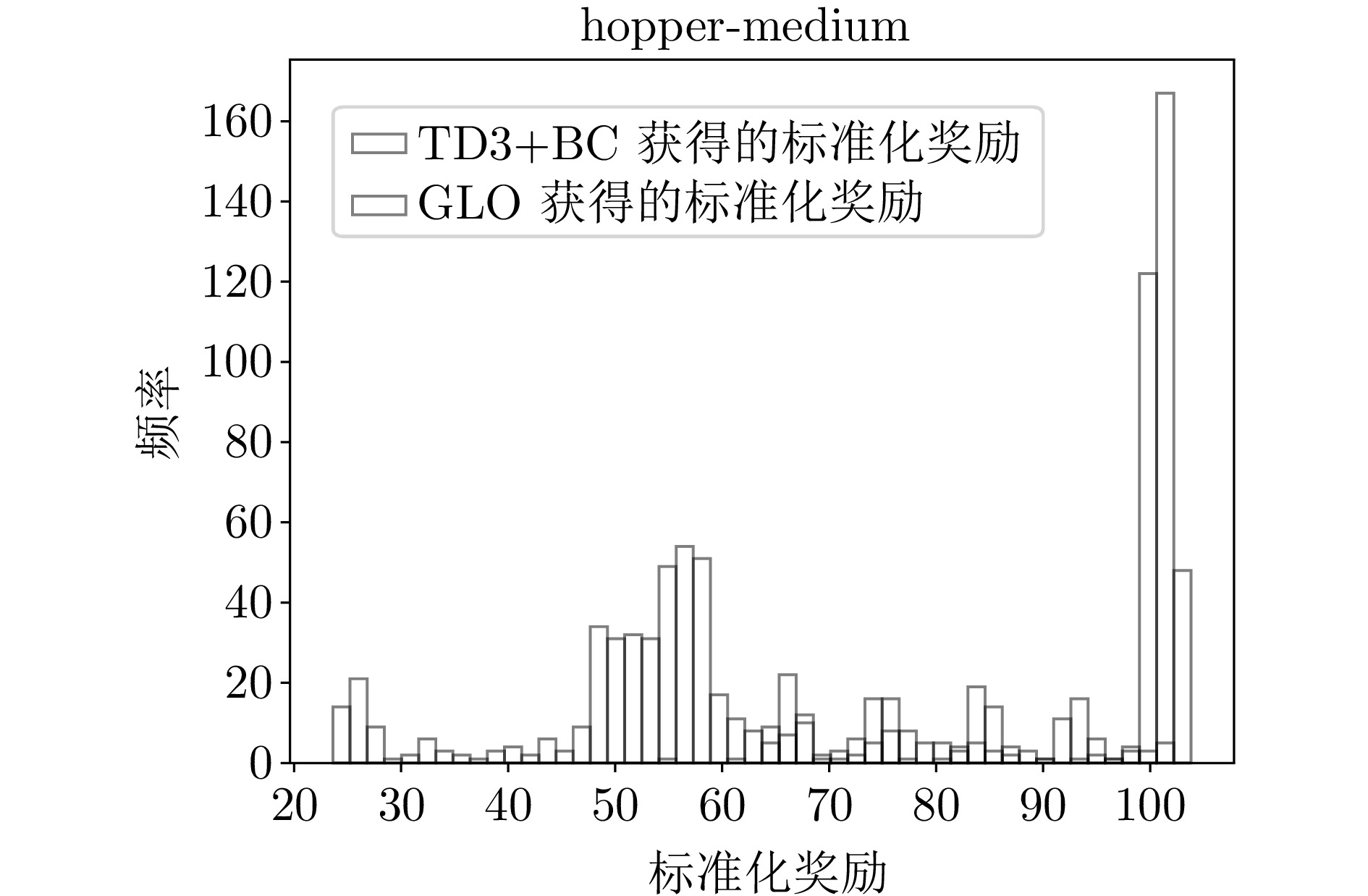
环境 TD3+BC IQL CQL Diffusion-QL SPOT wPC GLO halfcheetah-m 48.3±0.3 48.3±0.2 47.0±0.2 51.1±0.5 58.4±1.0 53.3 57.1±0.4 halfcheetah-m-r 44.6±0.5 44.5±0.2 45.0±0.3 47.8±0.3 52.2±1.2 48.3 48.0±0.3 halfcheetah-m-e 90.7±4.3 94.7±0.5 95.6±0.4 96.8±0.3 86.9±4.3 93.7 96.2±0.9 walker2d-m 83.7±2.1 80.9±3.2 80.7±3.3 87.0±0.9 86.4±2.7 86.0 90.2±1.3 walker2d-m-r 81.8±5.5 82.2±3.0 73.1±13.2 95.5±1.5 91.6±2.8 89.9 89.6±1.4 walker2d-m-e 110.1±0.5 111.7±0.9 109.6±0.4 110.1±0.3 112.1±0.5 110.1 111.8±1.2 hopper-m 59.3±4.2 67.5±3.8 59.1±3.8 90.5±4.6 86.0±8.7 86.5 94.1±1.7 hopper-m-r 60.9±18.8 97.4±6.4 95.1±5.3 101.3±0.6 100.2±1.9 97.0 99.2±1.6 hopper-m-e 98.4±9.4 107.4±7.8 99.3±10.9 111.1±1.3 99.3±7.1 95.7 111.7±1.4 平均 75.3 81.6 78.3 87.9 85.9 84.5 88.7 antmaze-umaze-v2 70.8±39.2 77.0±5.5 92.8±1.2 93.4±3.4 93.5±2.4 — 93.8±1.8 antmaze-umaze-diverse-v2 44.8±11.6 54.3±5.5 37.3±3.7 66.2±8.6 40.7±5.1 — 51.8±5.3 平均 55.0 65.7 65.0 79.8 67.1 — 72.8
下载: 导出CSV
表 4 不同算法对应的梯度范数
Table 4 The gradient norm of different algorithm
环境 TD3+BC GLO halfcheetah-m 2.0e-4 5.0e-5 halfcheetah-m-r 4.0e-4 1.2e-4 halfcheetah-m-e 2.2e-4 1.1e-4 walker2d-m 2.2e-4 8.7e-5 walker2d-m-r 4.1e-4 7.3e-4 walker2d-m-e 2.1e-4 3.0e-5 hopper-m 3.5e-4 5.2e-5 hopper-m-r 5.7e-4 1.0e-4 hopper-m-e 3.8e-4 3.0e-5 antmaze-umaze 1.6e-3 5.4e-4 antmaze-umaze-diverse 6.2e-4 2.9e-4
下载: 导出CSV
表 5 实验中初始状态的随机扰动设置
Table 5 Random noise settings for the initial state
环境 数据集随机扰动分布 测试随机扰动分布 halfcheetah [−0.1, 0.1] $ [-0.20,\;-0.15] \cup [0.15,\;0.20] $ walker2d [−0.005, 0.005] $ [-0.025,\;-0.01] \cup [0.01,\;0.025] $ hopper [−0.005, 0.005] $ [-0.025,\;-0.01] \cup [0.01,\;0.025] $
下载: 导出CSV
表 6 泛化能力测试时的平均标准化奖励
Table 6 Average normalized rewards in generalization testing
环境 TD3+BC GLO halfcheetah-m 47.0 56.4 halfcheetah-m-r 43.7 47.5 halfcheetah-m-e 89.9 93.8 walker2d-m 81.7 88.4 walker2d-m-r 77.9 87.6 walker2d-m-e 110.0 111.5 hopper-m 55.2 94.4 hopper-m-r 53.2 77.7 hopper-m-e 98.4 105.0 平均 73.0 84.7
下载: 导出CSV
表 7 消融实验实验结果
Table 7 Ablation experiment results
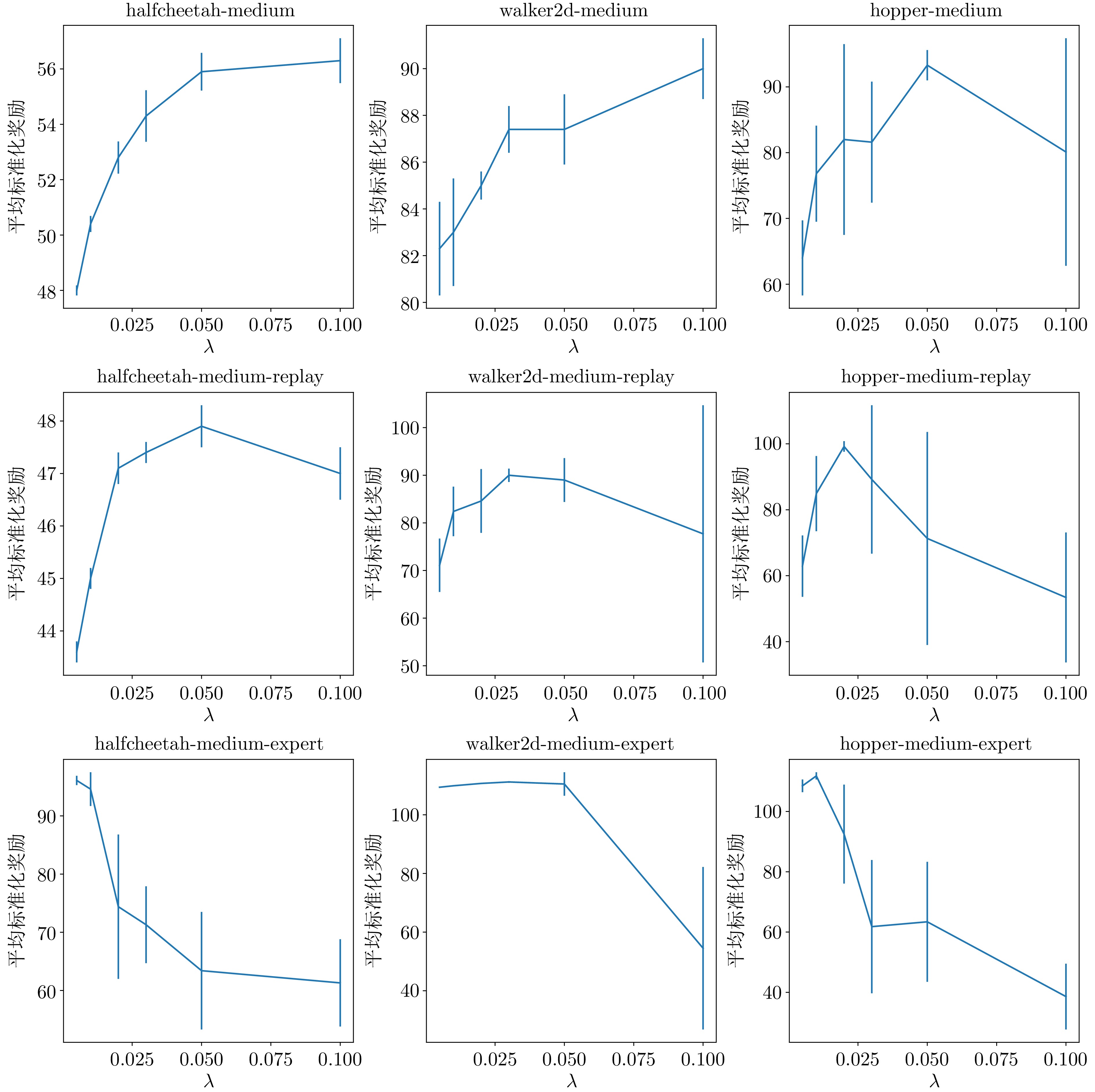
环境 TD3+BC 原损失函数(实验1) 无Q norm(实验2) 无反向软更新(实验3) GLO halfcheetah-m 48.3±0.3 49.5±0.2 57.5±1.2 58.0±0.3 57.1±0.4 halfcheetah-m-r 44.6±0.5 45.4±0.2 49.0±0.9 47.9±0.4 48.0±0.3 halfcheetah-m-e 90.7±4.3 96.3±0.5 87.7±4.5 96.1±0.8 96.2±0.9 walker2d-m 83.7±2.1 84.6±1.4 89.9±2.3 90.0±1.3 90.2±1.3 walker2d-m-r 81.8±5.5 66.8±30.7 85.6±2.6 89.6±1.3 89.6±1.4 walker2d-m-e 110.1±0.5 109.7±0.2 92.2±46.9 111.2±0.7 111.8±1.2 hopper-m 59.3±4.2 71.0±5.1 77.9±15.3 93.3±2.3 94.1±1.7 hopper-m-r 60.9±18.8 81.2±10.8 76.1±18.4 99.2±1.6 99.2±1.6 hopper-m-e 98.4±9.4 110.1±3.1 106.6±8.4 111.8±1.2 111.7±1.4 平均 75.3 79.4 80.3 88.5 88.7
下载: 导出CSV
表 8 不同数据集下拐点的$ \lambda$值
Table 8 The $\lambda$ corresponding to the inflection point in different datasets
环境 m m-r m-e halfcheetah 0.10 0.05 0.01 walker2d 0.10 0.03 0.03 Hopper 0.05 0.02 0.01
下载: 导出CSV
表 9 在线强化学习实验中设置的超参数
Table 9 Hyperparameters in online reinforcement learning experiments
环境 $ \alpha$ Ant 100 Halfcheetah 10 Hopper 10 invertedPendulum 1 reacher 100 inverteddoublePendulum 0.1 walker 0.1
下载: 导出CSV
表 10 在线强化学习中梯度损失函数的应用实验结果
Table 10 Experimental results of GLF in online reinforcement learning
环境 TD3 TD3+正则 ant 5094.5 ±1116.1 5340.0 ±343.8halfcheetah 9638.3 ±998.010577.1 ±660.0hopper 2427.3 ±1180.1 3371.6 ±142.0invertedPendulum 1000 1000 reacher −3.888±0.446 −3.896±0.433 inverteddoublePendulum 5765.2 ±4863.0 7480.4 ±4166.7 walker 3141.8 ±1142.6 4378.4 ±707.9
下载: 导出CSV
11 SPOT中梯度损失函数的应用实验结果
11 Experimental results of GLF in SPOT
环境 SPOT SPOT+正则 halfcheetah-m 58.4±1.0 60.1 ±1.2 halfcheetah-m-r 52.2±1.2 53.3±0.4 halfcheetah-m-e 86.9±4.3 92.8±0.6 walker2d-m 86.4±2.7 88.4±1.1 walker2d-m-r 91.6±2.8 92.7±2.4 walker2d-m-e 112.1±0.5 110.6±2.0 hopper-m 86.0±8.7 96.3±5.3 hopper-m-r 100.2±1.9 101.4±0.9 hopper-m-e 99.3±7.1 103.8±2.7 平均 85.9 88.8
下载: 导出CSV
-
[1] 刘全, 翟建伟, 章宗长, 钟珊, 周倩, 章鹏, 等. 深度强化学习综述. 计算机学报, 2018, 41(01): 1−27 doi: 10.11897/SP.J.1016.2018.00001Liu Quan, Zhai Jian-Wei, Zhang Zong-Chang, Zhong Shan, Zhou Qian, Zhang Peng, et al. A survey on deep reinforcement learning. Chinese Journal of Computers, 2018, 41(01): 1−27 doi: 10.11897/SP.J.1016.2018.00001 [2] 丁世飞, 杜威, 张健, 郭丽丽, 丁玲. 多智能体深度强化学习研究进展. 计算机学报, 2024, 47(7): 1547−1567Ding Shi-Fei, Du Wei, Zhang Jian, Guo Li-Li, Ding Ling. Research progress of multi-agent deep reinforcement learning. Chinese Journal of Computers, 2024, 47(7): 1547−1567 [3] 吴晓光, 刘绍维, 杨磊, 邓文强, 贾哲恒. 基于深度强化学习的双足机器人斜坡步态控制方法. 自动化学报, 2021, 47(8): 1974−1987Wu Xiao-Guang, Liu Shao-Wei, Yang Lei, Deng Wen-Qiang, Jia Zhe-Heng. A gait control method for biped robot on slope based on deep reinforcement learning. Acta Automatica Sinica, 2021, 47(8): 1974−1987 [4] 张威振, 何真, 汤张帆. 风扰下无人机栖落机动的强化学习控制设计. 上海交通大学学报, 2024, 58(11): 1753−1761Zhang Wei-Zhen, He Zhen, Tang Zhang-Fan. Reinforcement learning control design for perching maneuver of unmanned aerial vehicles with wind disturbances. Journal of Shanghai Jiao tong University, 2024, 58(11): 1753−1761 [5] Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guezet A, et al. Mastering the game of go without human knowledge. Nature, 2017, 550(7676): 354−359 doi: 10.1038/nature24270 [6] Vinyals O, Babuschkin I, Czarnecki W M, Mathieu M, Dudzik A, Chung J, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 2019, 575(7782): 350−354 doi: 10.1038/s41586-019-1724-z [7] 余宏晖, 林声宏, 朱建全, 陈浩悟. 基于深度强化学习的微电网在线优化. 电测与仪表, 2024, 61(4): 9−14Yu Hong-Hui, Lin Sheng-Hong, Zhu Jian-Quan, Chen Hao-Wu. On-line optimization of micro-grid based on deep reinforcement learning. Electric Measurement and Instrumentation, 2024, 61(4): 9−14 [8] 张沛, 陈玉鑫, 王光华, 李晓影. 基于图强化学习的配电网故障恢复决策. 电力系统自动化, 2024, 48(2): 151−158 doi: 10.7500/AEPS20230316001Zhang Pei, Chen Yu-Xin, Wang Guang-Hua, Li Xiao-Ying. Fault recovery decision of distribution network based on graph reinforcement learning. Automation of Electric Power Systems, 2024, 48(2): 151−158 doi: 10.7500/AEPS20230316001 [9] 刘健, 顾扬, 程玉虎, 王雪松. 基于多智能体强化学习的乳腺癌致病基因预测. 自动化学报, 2022, 48(5): 1246−1258Liu Jian, Gu Yang, Cheng Yu-Hu, Wang Xue-Song. Prediction of breast cancer pathogenic genes based on multi-agent reinforcement learning. Acta Automatica Sinica, 2022, 48(5): 1246−1258 [10] Choudhary K, Gupta D, Thomas P S. ICU-Sepsis: a benchmark MDP built from real medical data. arXiv preprint arXiv: 2406.05646, 2024. [11] 张兴龙, 陆阳, 李文璋, 徐昕. 基于滚动时域强化学习的智能车辆侧向控制算法. 自动化学报, 2023, 49(12): 2481−2492Zhang Xing-Long, Lu Yang, Li Wen-Zhang, Xu Xin. Receding horizon reinforcement learning algorithm for lateral control of intelligent vehicles. Acta Automatica Sinica, 2023, 49(12): 2481−2492 [12] 何逸煦, 林泓熠, 刘洋, 杨澜, 曲小波. 强化学习在自动驾驶技术中的应用与挑战. 同济大学学报(自然科学版), 2024, 52(4): 520−531 doi: 10.11908/j.issn.0253-374x.23397He Yi-Xu, Lin Hong-Yi, Liu Yang, Yang Lan, Qu Xiao-Bo. Application and challenges of reinforcement learning in autonomous driving technology. Journal of Tongji University (Natural Science), 2024, 52(4): 520−531 doi: 10.11908/j.issn.0253-374x.23397 [13] Vasco M, Seno T, Kawamoto K, Subramanian K, Wurman P R, Stone P. A super-human vision-based reinforcement learning agent for autonomous racing in gran turismo. arXiv preprint arXiv: 2406.12563, 2024. [14] 刘扬, 何泽众, 王春宇, 郭茂祖. 基于DDPG算法的末制导律设计研究. 计算机学报, 2021, 44(9): 1854−1865 doi: 10.11897/SP.J.1016.2021.01854Liu Yang, He Ze-Zhong, Wang Chun-Yu, Guo Mao-Zu. Terminal guidance law design based on DDPG algorithm. Chinese Journal of Computers, 2021, 44(9): 1854−1865 doi: 10.11897/SP.J.1016.2021.01854 [15] Levine S, Kumar A, Tucker G, Fu J. Offline reinforcement learning: tutorial, review, and perspectives on open problems. arXiv preprint arXiv: 2005.01643, 2020. [16] 王雪松, 王荣荣, 程玉虎. 安全强化学习综述. 自动化学报, 2023, 49(9): 1813−1835Wang Xue-Song, Wang Rong-Rong, Cheng Yu-Hu. Safe reinforcement learning: a survey. Acta Automatica Sinica, 2023, 49(9): 1813−1835 [17] Fujimoto S, Gu S S. A minimalist approach to offline reinforcement learning. Advances in neural information processing systems, 2021, 34: 20132−20145 [18] Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods. In: Proceedings of the 35th International Conference on Machine Learning. Stockholm Sweden: PMLR, 2018.1587−1596 [19] Torabi F, Warnell G, Stone P. Behavioral cloning from observation. arXiv preprint arXiv: 1805.01954, 2018. [20] Wu J, Wu H, Qiu Z, Wang J, Long M. Supported policy optimization for offline reinforcement learning. Advances in Neural Information Processing Systems, 2022, 35: 31278−31291 [21] Kingma D P, Welling M. Auto-encoding variational bayes. arXiv preprint arXiv: 1312.6114, 2013. [22] Wang Z, Hunt J J, Zhou M. Diffusion policies as an expressive policy class for offline reinforcement learning. arXiv preprint arXiv: 2208.06193, 2022. [23] Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models. Advances in neural information processing systems, 2020, 33: 6840−6851 [24] Tarasov D, Nikulin A, Akimov D, Kurenkov V, Kolesnikov S. CORL: Research-oriented deep offline reinforcement learning library. Advances in Neural Information Processing Systems, 2023, 36: 30997−31020 [25] Hochreiter S, Schmidhuber J. Flat minima. Neural computation, 1997, 9(1): 1−42 doi: 10.1162/neco.1997.9.1.1 [26] Zhao Y, Zhang H, Hu X. Penalizing gradient norm for efficiently improving generalization in deep learning. In: Proceedings of the 39th International Conference on Machine Learning. Baltimore, Maryland, USA: PMLR, 2022.26982−26992 [27] Gao C, Xu K, Liu L, Ye D, Zhao P, Xu Z. Robust Offline Reinforcement Learning with Gradient Penalty and Constraint Relaxation. arXiv preprint arXiv: 2210.10469, 2022. [28] Fu J, Kumar A, Nachum O, Tucker G, Levine S. D4rl: Datasets for deep data-driven reinforcement learning. arXiv preprint arXiv: 2004.07219, 2020. [29] Sutton R S, Barto A G. Reinforcement Learning: An Introduction (2nd edition). Cambridge: MIT Press, 2018 [30] Sutton R S, McAllester D, Singh S, Mansour Y. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems, 199912 [31] Kumar A, Zhou A, Tucker G, Levine S. Conservative q-learning for offline reinforcement learning. Advances in neural information processing systems, 2020, 33: 1179−1191 [32] Kostrikov I, Nair A, Levine S. Offline reinforcement learning with implicit q-learning. arXiv preprint arXiv: 2110.06169, 2021. [33] Peng Z, Han C, Liu Y, Zhou Z. Weighted policy constraints for offline reinforcement learning. In: Proceedings of the 37th AAAI Conference on Artificial Intelligence. Washington, USA: AAAI Press, 2023. 9435−9443 -
计量
- 文章访问数: 40
- HTML全文浏览量: 35
- 被引次数: 0
