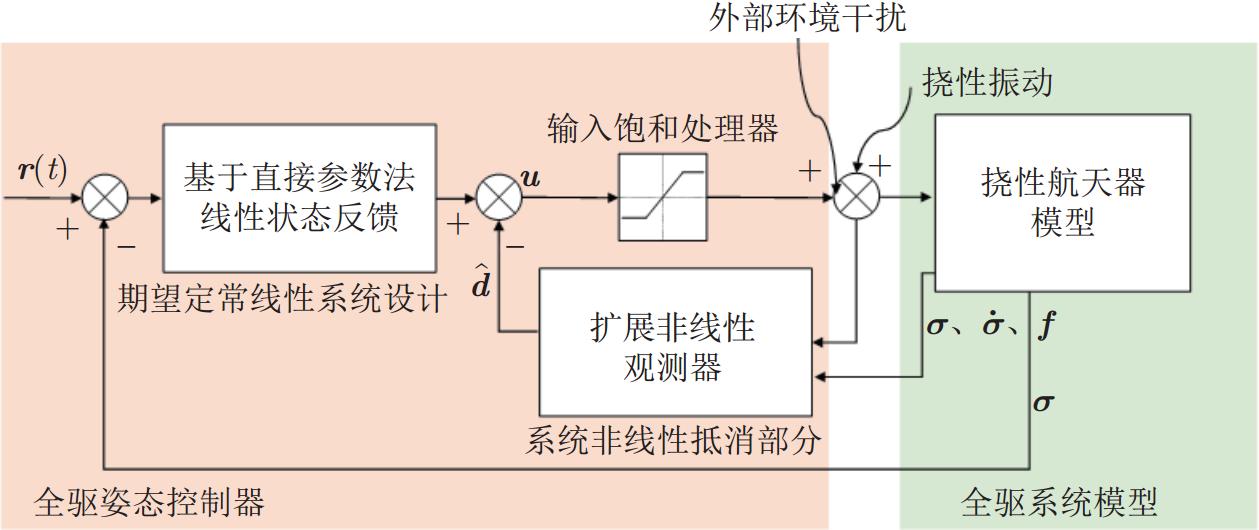
-
摘要: 面向空间攻防等任务的航天器通常安装微波、激光等大功率对抗载荷, 未来航天器需要装备大型挠性太阳能帆板. 针对挠性航天器姿态机动过程中存在外部干扰、执行机构饱和及挠性附件振动且挠性模态不易直接测量等问题, 提出带挠性附件航天器的全驱姿态控制方法. 首先, 建立挠性航天器全驱姿态控制模型. 其次, 基于扩展非线性观测器(Extended nonlinearity observer, ENO)与努斯鲍姆增益调节设计一种抗饱和的姿态控制鲁棒算法. 将外部扰动、挠性振动和输入饱和函数饱和估计误差作为复合干扰, 采用非线性干扰观测器对其进行有效补偿. 在直接参数设计线性控制参数基础上, 扩展非线性观测器负责对挠性航天器产生的挠性振动进行实时估计和补偿, 努斯鲍姆函数辅助控制器输出力矩避免饱和, 并利用李雅普诺夫方法严格证明闭环系统的稳定性. 最后通过数学仿真验证该方法不仅能够实现执行机构饱和约束条件下的姿态控制, 还能有效抑制挠性结构的振动, 为探索未来带有大型挠性附件航天器姿态控制新的方法提供参考.Abstract: For space missions such as space attack and defense, spacecrafts are usually equipped with high-power counter loads such as microwaves and lasers, thus future spacecrafts will need to be equipped with large-scale flexible solar panels. To solve the problems of external interference, actuator saturation, and vibration of flexible attachments difficult to measure directly during attitude maneuver of flexible spacecraft, a fully actuated-based attitude control method for flexible spacecraft is proposed. First, a fully actuated attitude model for flexible spacecraft is established. Second, a robust attitude control algorithm against saturation is designed based on the extended nonlinear observer (ENO) and Nussbaum gain adjustment. The external perturbation, flexible vibration, and the approximation error of the input saturation function are considered composite disturbances, which are efficiently compensated by the nonlinear disturbance observer. Based on the direct parametric design of linear control parameters, the ENO is responsible for the real-time estimation and compensation of flexural vibration generated by the flexible spacecraft. And the Nussbaum function is used for the adjustment of the controller output torque magnitude to avoid actuator saturation. The stability of the closed-loop system is rigorously demonstrated using the Lyapunov method. Finally, it is verified by mathematical simulation that this method can not only realize the attitude control under the actuator saturation constraint but also effectively suppress the flexible vibration, which contributes to exploring a novel method for the attitude control of spacecraft with large-scale flexural attachments in the future.
-
图 9 自适应参数${\boldsymbol{\chi}}$的时间响应
Fig. 9 Time response of adaptive parameter ${\boldsymbol{\chi}}$
表 1 仿真参数
Table 1 Simulation parameters
物理参数 值 转动惯量矩阵$ (\text{kg}\cdot\text{m}^{2}) $ ${\boldsymbol{J} }=\text{diag}\{40,\;150,\;160\}$ 耦合矩阵 $ {\boldsymbol{\delta}}= \left[\begin{array}{*{20}{r}} 1.352\ 3 & 1.278\ 4 & 2.155\ 3\\-1.151\ 9 & 1.017\ 6 & -1.272\ 4\\2.216\ 7 & 1.589\ 1 & -0.832\ 4\\1.236\ 4 & -1.653\ 7 & 1.225\ 1\end{array}\right] $ 挠性模态数 $ N=4 $ 固有频率(rad/s) $ {\boldsymbol{\Lambda}}=[1.20, \; 2.48 ,\; 3.37, \; 7.47] $ 阻尼比 $ \xi_1 = \xi_2 = \xi_3 = \xi_4 = 0.01 $ 外部干扰矩阵(N·m) $ d=10^{-4}\begin{bmatrix}3\cos(0.1t)+4\\1.5\sin(0.1t)+3\cos(0.1t)\\3\sin(0.1t)+1\end{bmatrix} $ 
下载: 导出CSV
表 2 各控制器参数
Table 2 Parameters of controllers
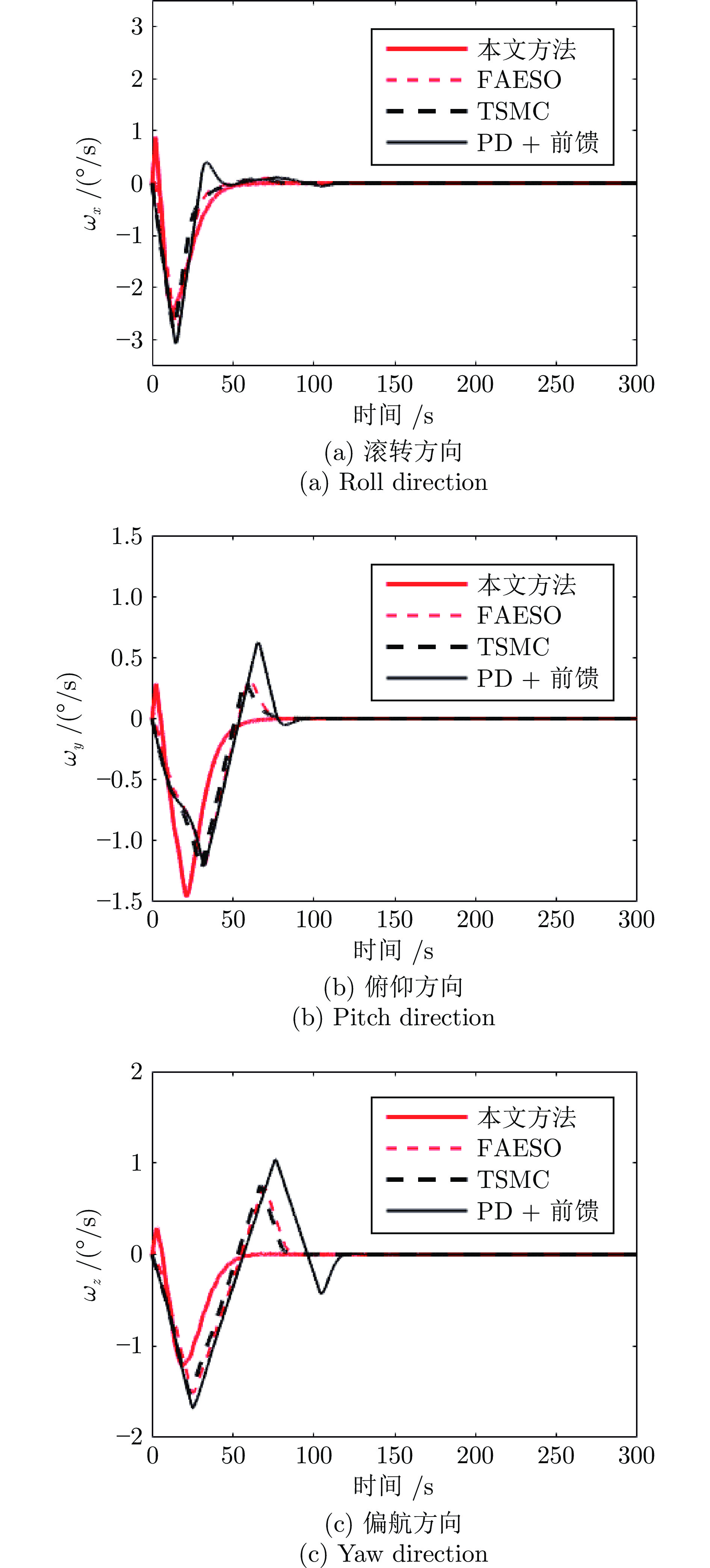
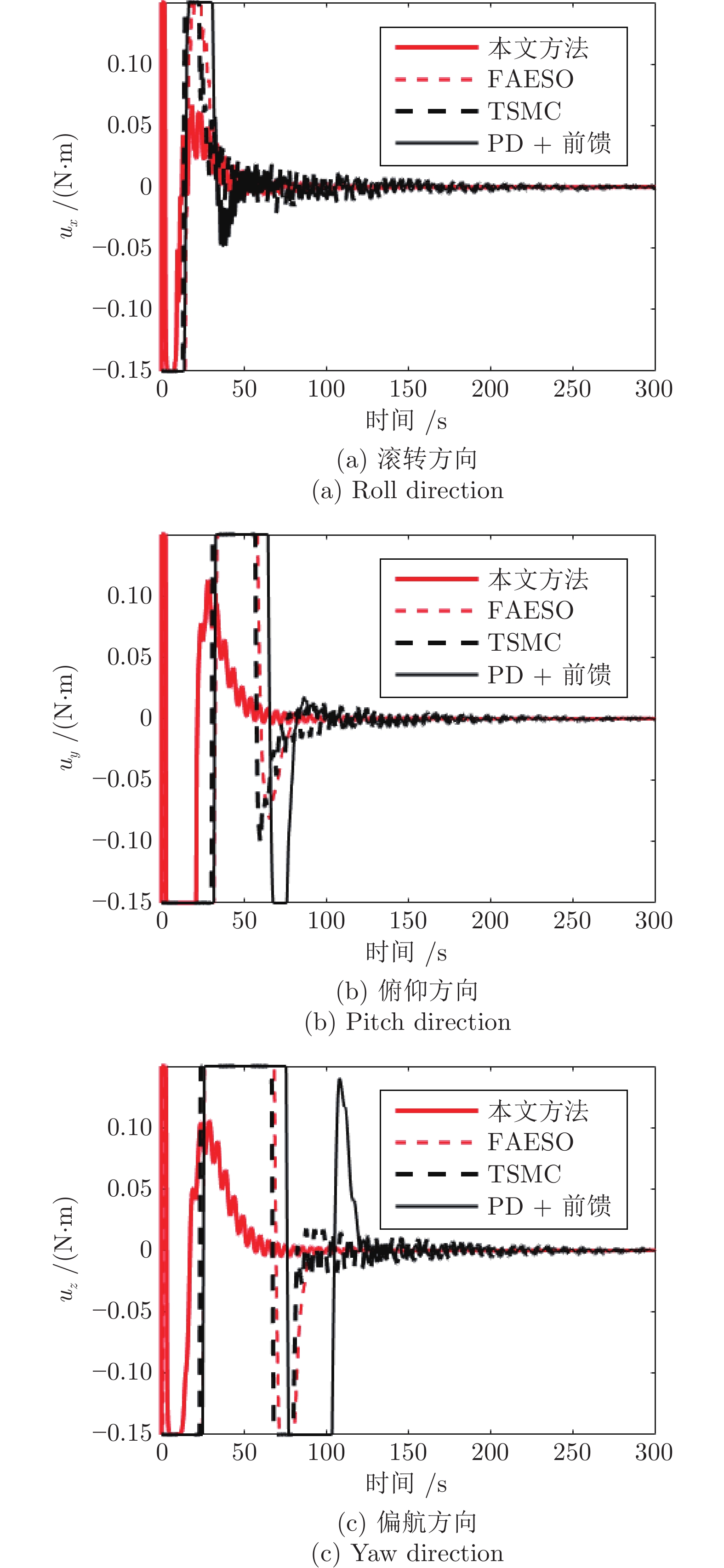
控制方法 控制律 控制参数 PD + 前馈补偿 $ {\boldsymbol{u}} = {{\boldsymbol{B}}^{ - 1}}({{\boldsymbol{A}}_p}{\boldsymbol{\sigma}} {\rm{ + }}{{\boldsymbol{A}}_d}\dot{{\boldsymbol{\sigma}}} ) - {{\boldsymbol{B}}^{ - 1}}({{\boldsymbol{f}}_{\rm{2}}} + {{\boldsymbol{f}}_{\rm{3}}}) $ $\begin{array}{l} { {\boldsymbol{A} }_p} = {\rm{diag}}\{ - 0 .12 ,\; - 0.12 ,\; - 0.12 \}\\ { {\boldsymbol{A} }_d} = {\rm{diag\{ - 0.7 ,\; - 0.7,\; - 0.7} }\} \end{array}$ TSMC $ {\boldsymbol{u}} = - { {{\beta q} \over p}}{{\boldsymbol{B}}^{ - 1}}{\dot{{\boldsymbol{\sigma}}} ^{{\rm{(2}} - { {p \over q}}{\rm{)}}}} - {{\boldsymbol{B}}^{ - 1}}({{\boldsymbol{f}}_{\rm{2}}} + {{\boldsymbol{f}}_{\rm{3}}}) + \varepsilon \text{sgn} (s) $ $ \beta = 0.8,\;\varepsilon = 0.002,\; p = 5,\;q = 3 $ FAESO $ {\boldsymbol{u}} {\rm{ = }}{{\boldsymbol{B}}^{ - 1}}{\boldsymbol{Z}}{{\boldsymbol{F}}^2}{{\boldsymbol{V}}^{ - 1}}{[\sigma, {\rm{ }}\dot \sigma ]^{\rm{T}}} - {{\boldsymbol{B}}^{ - 1}}{\rm{(}}{\hat {{\boldsymbol{z}}}_3}{\rm{ + }}{{\boldsymbol{f}}_1}{\rm{)}} $ $\begin{array}{c} {\boldsymbol{F} } = \left[ \begin{array}{l} {\rm{diag} }\{ - 0.09,\; - 0.1,\; - 0.08\}\quad\ { {\boldsymbol{O} }_{3 \times 3} } \\ { {\boldsymbol{O} }_{3 \times 3{\rm{ } } } }\quad {\rm{diag} }\{ - 0.35,\; - 0.4,\; - 0.35\} \end{array} \right] \\ {\boldsymbol{Z} } = [{ {\boldsymbol{I} }_{3 \times 3} },\;\ { {\boldsymbol{I} }_{3 \times 3} }],\;kv = 0.8,\;k = 0.6 \\ \left[\beta_1,\; \beta_2,\; \beta_3\right]=\left[50,\; 150,\; 500\right],\;{ {\boldsymbol{z} }_{\rm{1} } } = {\bf{0} },\; { {\boldsymbol{z} }_{\rm{2} } } = {\bf{0} },\; { {\boldsymbol{z} }_{\rm{3} } } = {\bf{0} } \end{array}$ 本文方法 式(15)$ \sim $式(17) $\begin{array}{c} {\boldsymbol{F} } = \left[ \begin{array}{l} {\rm{diag} }\{ - 0.09,\; - 0.1,\; - 0.08\}\; { {\boldsymbol{O} }_{3 \times 3} }\\{ {\boldsymbol{O} }_{3 \times 3{\rm{ } } } }\; {\rm{diag} }\{ - 0.35,\; - 0.4,\; - 0.35\} \end{array} \right]\\{\boldsymbol{P} } = \left[ {\begin{array}{*{20}{c} } { {\rm{diag} }\{35,\;35,\;35\}\; {\rm{diag} }\{80,\;80,\;70\}}\\{ {\rm{diag} }\{80,\;80,\;80\}\;{\rm{diag} }\{150,\;150,\;150\}} \end{array} } \right]\\kv = 0.8,\;k = 0.6,\;\varsigma = 0.6,\; {\boldsymbol{Z} } = [{ {\boldsymbol{I} }_{3 \times 3} }{\rm{ } },\; { {\boldsymbol{I} }_{3 \times 3} }],\; {\boldsymbol{\chi} } (0){\rm{ = } }{\bf{0} }\\ \left[\beta_1,\; \beta_2,\; \beta_3\right]=\left[50,\; 150,\; 500\right],\;{ {\boldsymbol{z} }_{\rm{1} } } = {\bf{0} },\; { {\boldsymbol{z} }_{\rm{2} } } = {\bf{0} },\; { {\boldsymbol{z} }_{\rm{3} } } = {\bf{0} } \end{array}$
下载: 导出CSV
-
[1] 杨广华, 王强, 陈国玖, 秘倩. 美国“星链”低轨星座军事应用前景探析. 中国航天, 2022 (9): 60−63Yang Guang-Hua, Wang Qiang, Chen Guo-Jiu, Mi Qian. Future military application of the US starlink LEO constellation. Aerospace China, 2022 (9): 60−63 [2] Gu D K, Liu G P, Duan G R. Parametric control to a type of quasi-linear second-order systems via output feedback. International Journal of Control, 2019, 92(2): 291−302 doi: 10.1080/00207179.2017.1350885 [3] Yao Q J, Li Q, Huang J C, Jahanshahi H. PDE-based prescribed performance adaptive attitude and vibration control of flexible spacecraft. Aerospace Science and Technology, 2023, 141: Article No. 108504 doi: 10.1016/j.ast.2023.108504 [4] Li A, Liu M, Shi Y. Adaptive sliding mode attitude tracking control for flexible spacecraft systems based on the Takagi-Sugeno fuzzy modelling method. Acta Astronautica, 2020, 175: 570−581 doi: 10.1016/j.actaastro.2020.05.041 [5] Ghorbani H, Vatankhah R, Farid M. Adaptive nonsingular fast terminal sliding mode controller design for a smart flexible satellite in general planar motion. Aerospace Science and Technology, 2021, 119: Article No. 107100 doi: 10.1016/j.ast.2021.107100 [6] Hasan M N, Haris M, Qin S Y. Flexible spacecraft's active fault-tolerant and anti-unwinding attitude control with vibration suppression. Aerospace Science and Technology, 2022, 122: Article No. 107397 doi: 10.1016/j.ast.2022.107397 [7] Xiao Y, de Ruiter A, Ye D, Sun Z W. Adaptive fault-tolerant attitude tracking control for flexible spacecraft with guaranteed performance bounds. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(3): 1922−1940 doi: 10.1109/TAES.2021.3123295 [8] 张慧凤, 董乐伟, 魏新江. 一类带有输入饱和的随机系统抗干扰控制. 自动化学报, 2021, 47(6): 1453−1459Zhang Hui-Feng, Dong Le-Wei, Wei Xin-Jiang. Anti-disturbance control for a class of stochastic systems with input saturation. Acta Automatica Sinica, 2021, 47(6): 1453−1459 [9] 高阳, 吴文海, 王子健. 具有输入约束和输出噪声的不确定系统级联线性自抗扰控制. 自动化学报, 2022, 48(3): 843−852Gao Yang, Wu Wen-Hai, Wang Zi-Jian. Cascaded linear active disturbance rejection control for uncertain systems with input constraint and output noise. Acta Automatica Sinica, 2022, 48(3): 843−852 [10] 彭秀艳, 贾书丽, 张彪. 一类具有执行器饱和的非线性系统抗饱和方法研究. 自动化学报, 2016, 42(5): 798−804Peng Xiu-Yan, Jia Shu-Li, Zhang Biao. Anti-saturation method for a class of nonlinear systems with actuator saturation. Acta Automatica Sinica, 2016, 42(5): 798−804 [11] Piltan F, Mirzaei M, Shahriari F, Nazari I, Emamzadeh S. Design baseline computed torque controller. International Journal of Engineering, 2012, 6(3): 129−141 [12] Sancak K V, Bayraktaroglu Z Y. Nonlinear computed torque control of 6-dof parallel manipulators. International Journal of Control, Automation and Systems, 2022, 20(7): 2297−2311 doi: 10.1007/s12555-021-0198-6 [13] 段广仁. 高阶系统方法——II. 能控性与全驱性. 自动化学报, 2020, 46(8): 1571−1581Duan Guang-Ren. High-order system approaches: II. Controllability and full-actuation. Acta Automatica Sinica, 2020, 46(8): 1571−1581 [14] Duan G R. High-order fully actuated system approaches: Part III. Robust control and high-order backstepping. International Journal of Systems Science, 2021, 52(5): 952−971 doi: 10.1080/00207721.2020.1849863 [15] Duan G R. High-order fully actuated system approaches: Part IV. Adaptive control and high-order backstepping. International Journal of Systems Science, 2021, 52(5): 972−989 doi: 10.1080/00207721.2020.1849864 [16] Duan G R. High-order fully actuated system approaches: Part V. Robust adaptive control. International Journal of Systems Science, 2021, 52(10): 2129−2143 doi: 10.1080/00207721.2021.1879964 [17] Duan G R. High-order fully actuated system approaches: Part VIII. Optimal control with application in spacecraft attitude stabilisation. International Journal of Systems Science, 2022, 53(1): 54−73 doi: 10.1080/00207721.2021.1937750 [18] Xiao F Z, Chen L Q. Attitude control of spherical liquid-filled spacecraft based on high-order fully actuated system approaches. Journal of Systems Science and Complexity, 2022, 35(2): 471−480 doi: 10.1007/s11424-022-2055-y [19] Liu X Q, Chen M Y, Sheng L, Zhou D H. Adaptive fault-tolerant control for nonlinear high-order fully-actuated systems. Neurocomputing, 2022, 495: 75−85 doi: 10.1016/j.neucom.2022.04.129 [20] Hu Q L, Shao X D, Guo L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Transactions on Mechatronics, 2018, 23(1): 331−341 doi: 10.1109/TMECH.2017.2775626 [21] Chen Z Y. Nussbaum functions in adaptive control with time-varying unknown control coefficients. Automatica, 2019, 102: 72−79 doi: 10.1016/j.automatica.2018.12.035 [22] Ioannou P A, Sun J. Robust Adaptive Control. Prentice Hall: Upper Saddle River, 1996. [23] Feng Z Y, Liu M, Cao X B. A fully-actuated system approach for spacecraft attitude control with input saturation. In: Proceedings of the 2nd Conference on Fully Actuated System Theory and Applications (CFASTA). Qingdao, China: IEEE, 2023. [24] 段广仁. 高阶系统方法——I. 全驱系统与参数化设计. 自动化学报, 2020, 46(7): 1333−1345Duan Guang-Ren. High-order system approaches: I. Fully-actuated systems and parametric designs. Acta Automatica Sinica, 2020, 46(7): 1333−1345 [25] Zhao Q, Duan G R. Fully actuated system approach for 6DOF spacecraft control based on extended state observer. Journal of Systems Science and Complexity, 2022, 35(2): 604−622 doi: 10.1007/s11424-022-1498-5 -
图(9) / 表(2)
计量
- 文章访问数: 143
- HTML全文浏览量: 121
- PDF下载量: 33
- 被引次数: 0
