Layer-wise Increment Decomposition-based Neuron Relevance Explanation for Deep Networks
-
摘要: 神经网络的黑箱特性严重阻碍了人们关于网络决策的直观分析与理解. 尽管文献报道了多种基于神经元贡献度分配的决策解释方法, 但是现有方法的解释一致性难以保证, 鲁棒性更是有待改进. 本文从神经元相关性概念入手, 提出一种基于逐层增量分解的神经网络解释新方法LID-Taylor (Layer-wise increment decomposition), 且在此基础上先后引入针对顶层神经元相关性的对比提升策略, 以及针对所有层神经元相关性的非线性提升策略, 最后利用交叉组合策略得到最终方法SIG-LID-IG, 实现了决策归因性能的鲁棒跃升. 通过热力图对现有工作与提出方法的决策归因性能做了定性定量评估. 结果显示, SIG-LID-IG在神经元的正、负相关性的决策归因合理性上均可媲美甚至优于现有工作. SIG-LID-IG在多尺度热力图下同样取得了精确性更高、鲁棒性更强的决策归因.Abstract: The black box nature of deep neural networks seriously hinders one＇s intuitive analysis and understanding of network decision-making. Although various decision explanation methods based on neural contribution allocation have been reported in the literature, the consistency of existing methods is difficult to ensure, and their robustness still needs improvement. This article starts with the concept of neuron relevance and proposes a new neural network explanation method LID-Taylor (layer-wise increment decomposition). Aiming at LID-Taylor, a contrast lifting strategy for top-layer neuron relevance and a non-linear lifting strategy for all-layer neuron relevance are introduced, respectively. Finally, a cross combination strategy is applied, obtaining the final method SIG-LID-IG and achieving a robust leap in decision attribution performance. Both qualitative and quantitative evaluation have been conducted via heatmaps on the decision attribution performance of existing works and the proposed method. Results show that SIG-LID-IG is comparable or even superior to existing works in the rationality of positive and negative relevance of neurons in decision-making attribution. SIG-LID-IG has also achieved better accuracy and stronger robustness in decision-making attribution in terms of multi-scale heatmaps.
-
图 2 增量相关性的逐层分配与吸收
Fig. 2 Layer-wise distribution and absorption of the increment relevance
图 3 本文神经元相关性解释方法的全景图
Fig. 3 Panorama of the neuron relevance explanation methods in this article
图 5 决策类别为牛獒时不同解释方法单尺度热力图展示 (从左至右: s5、s4、s3、s2、s1; 从上到下: SIG-LID-Taylor、LID-IG、SIG-LID-IG)
Fig. 5 Single-scale heatmaps of different explanation methods when the decision category is bull mastiff (From left to right: s5, s4, s3, s2, s1; From top to bottom: SIG-LID-Taylor, LID-IG, SIG-LID-IG)
图 6 决策类别为虎猫时不同解释方法单尺度热力图展示 (从左至右: s5、s4、s3、s2、s1; 从上到下: SIG-LID-Taylor、LID-IG、SIG-LID-IG)
Fig. 6 Single-scale heatmaps of different explanation methods when the decision category is tiger cat (From left to right: s5, s4, s3, s2, s1; From top to bottom: SIG-LID-Taylor, LID-IG, SIG-LID-IG)
图 7 不同方法的第5阶段单尺度热力图对比 (从左至右: GradCAM、LayerCAM、ScoreCAM、IG、LRP-0、SG-LRP-ZP、SIG-LID-Taylor、LID-IG、SIG-LID-IG)
Fig. 7 Comparison of stage 5 single-scale heatmaps for different methods (From left to right: GradCAM, LayerCAM, ScoreCAM, IG, LRP-0, SG-LRP-ZP, SIG-LID-Taylor, LID-IG, SIG-LID-IG)
图 9 LayerCAM与SIG-LID-IG在不同多尺度热力图下的PC评估折线图
Fig. 9 Line chart of PC evaluation between LayerCAM and SIG-LID-IG with different multi-scale heatmaps
图 13 SG-LRP-ZP和SIG-LID-IG的多尺度热力图对比
Fig. 13 Comparison of multi-scale heatmaps between SG-LRP-ZP and SIG-LID-IG
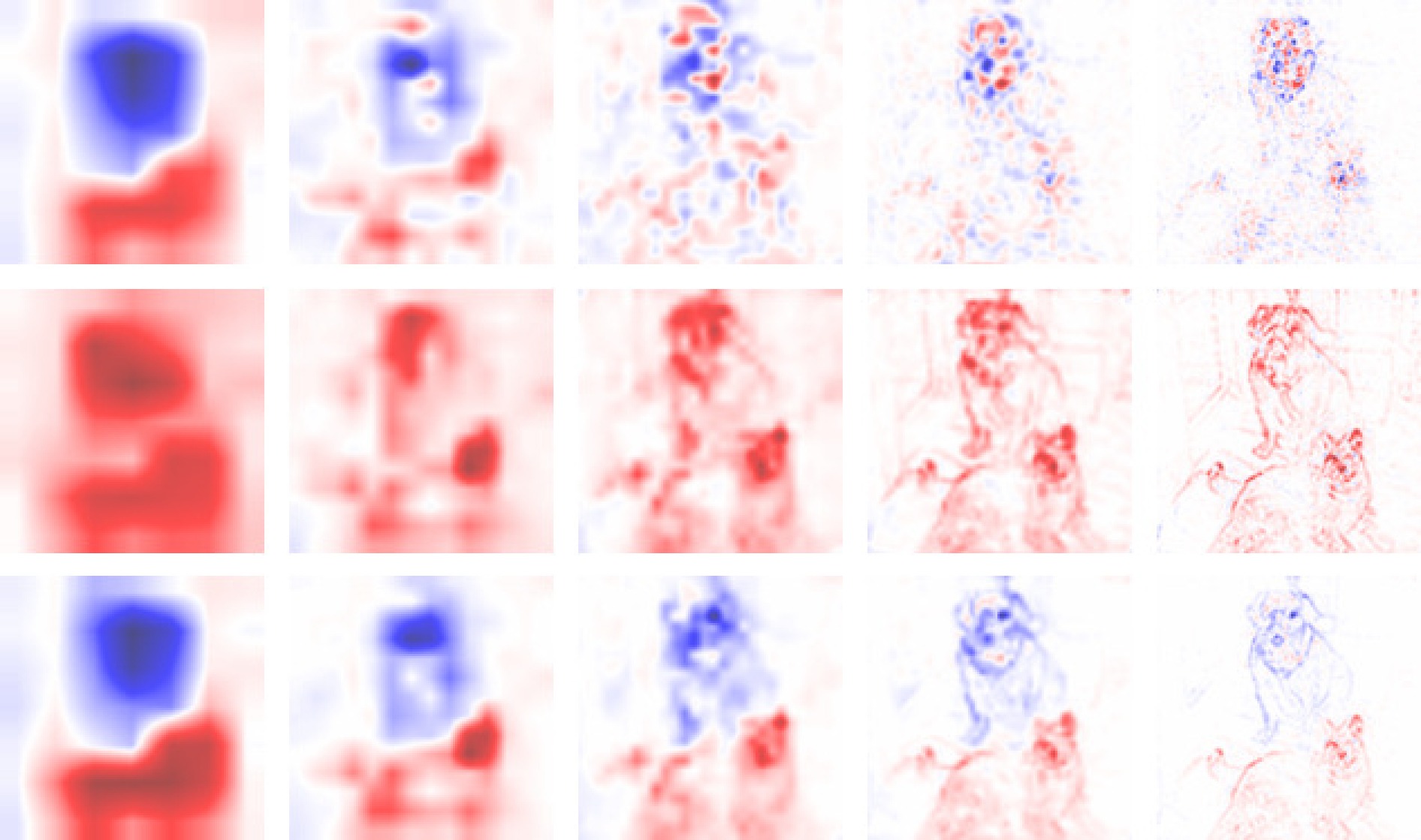
图 14 热力图的归因鲁棒性 (左, 右分别对应大灰猫头鹰和墨西哥鲵的两组平移缩放样本; 上、下分别为ST-LID-Taylor和SIG-LID-Taylor的热力图结果)
Fig. 14 Attribution robustness of heatmaps (Left and right correspond to the two groups of translation and scaling samples of great gray owl and Mexican salamander, respectively. The top and bottom show the heatmap results of ST-LID-Taylor and SIG-LID-Taylor, respectively)
表 1 不同方法的逐层规则对比
Table 1 Layer-wise rule comparison of different methods
方法名 LRP-0 LID-Taylor 顶层 $e_c\odot Z$ $e_c\odot\Delta Z$ 线性层 LRP-0 LID-Taylor 非线性层 Pass, WTA LID-Taylor 方法名 ST-LID-Taylor SIG-LID-IG 顶层 ST SIG 线性层 LID-Taylor LID-Taylor* 非线性层 LID-Taylor LID-IG 
下载: 导出CSV
表 2 顶层相关性对比
Table 2 Comparison of top layer relevance
方法名 顶层相关性 LRP-0 $e_c\odot Z$ LID-Taylor $e_c\odot \Delta Z$ SG-LRP $P_c'$ ST-LID-Taylor $P_c'\odot \Delta Z$ SIG-LID-IG $\bar{P}_c'\odot \Delta Z$
下载: 导出CSV
表 3 中间层规则对比
Table 3 Comparison of middle layer rule
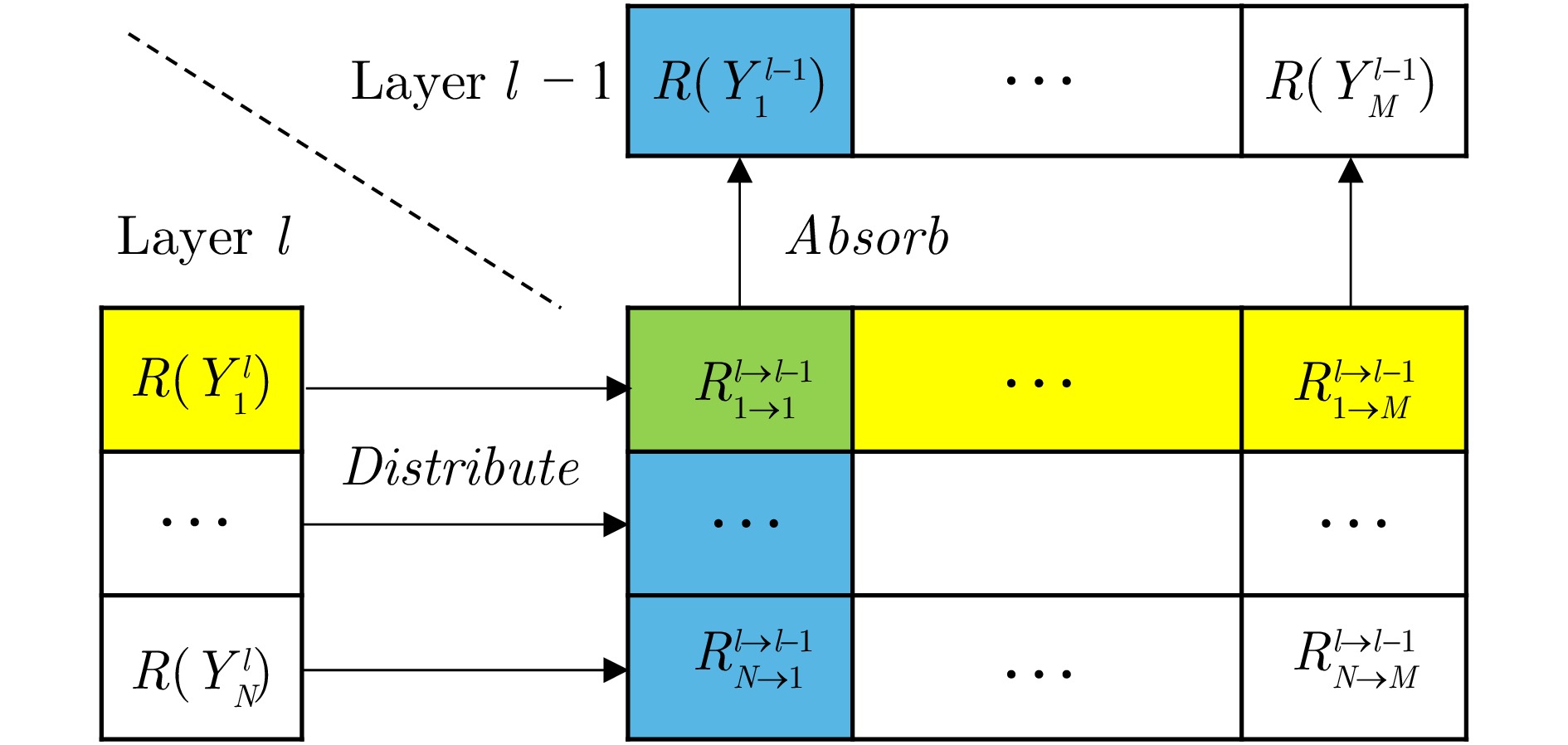
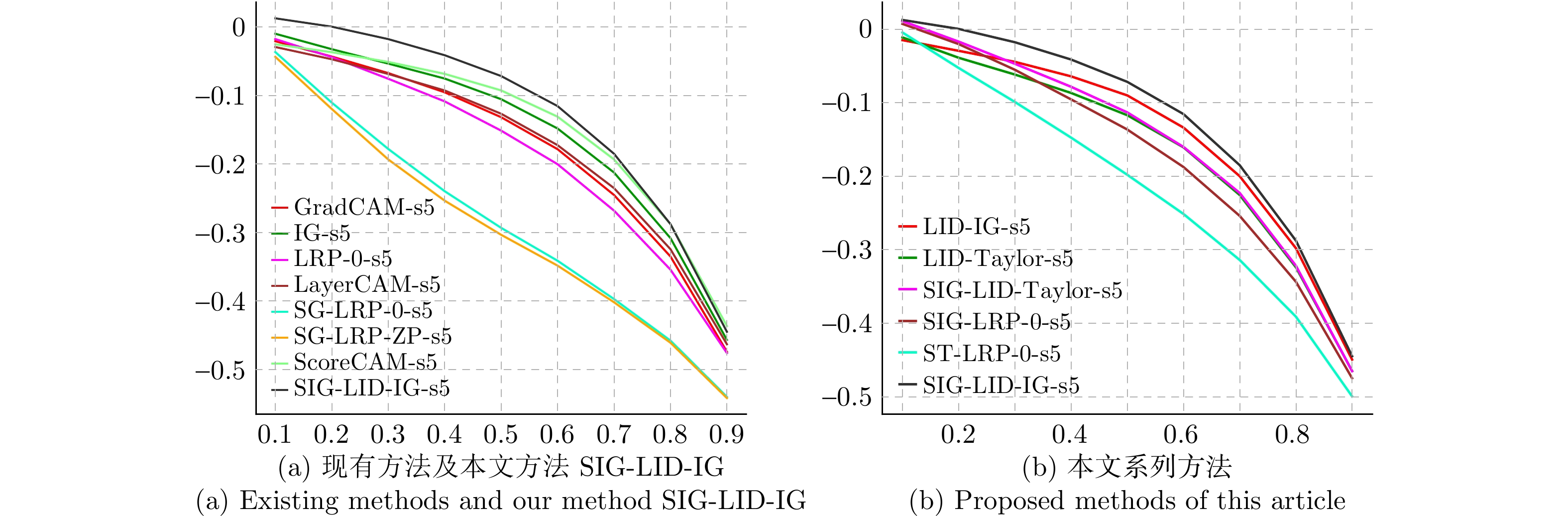
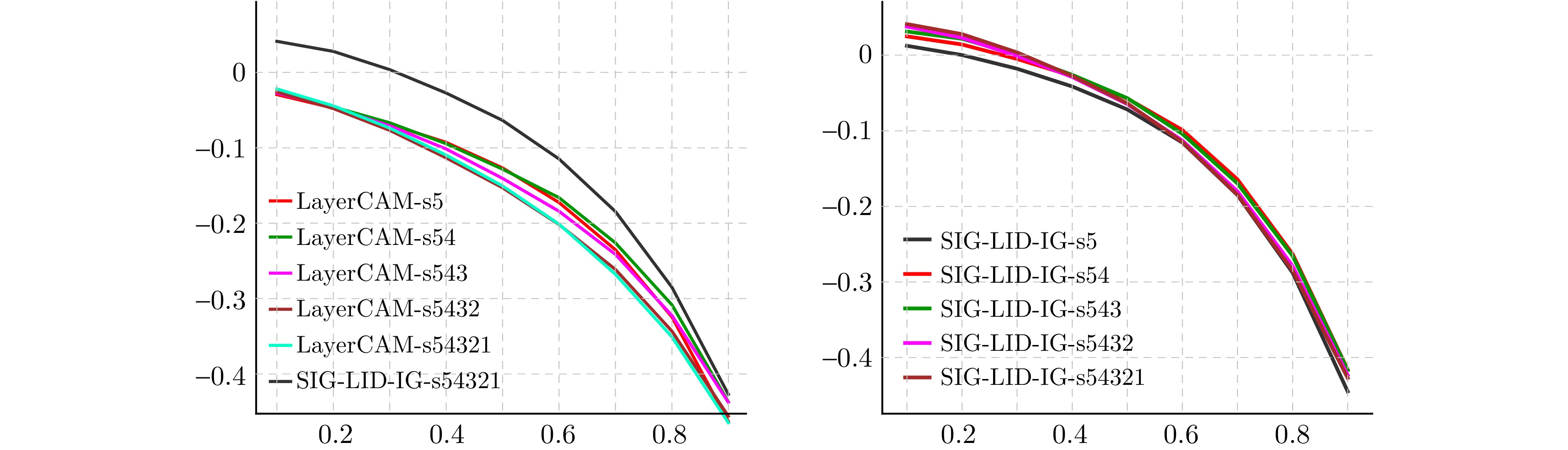
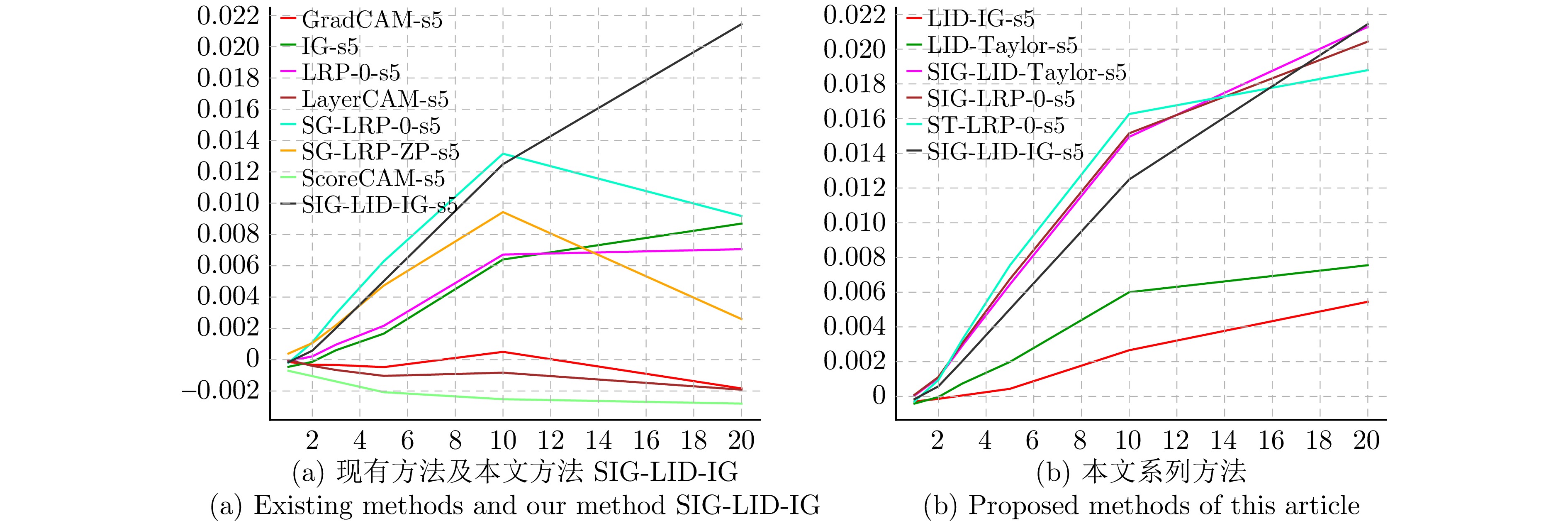
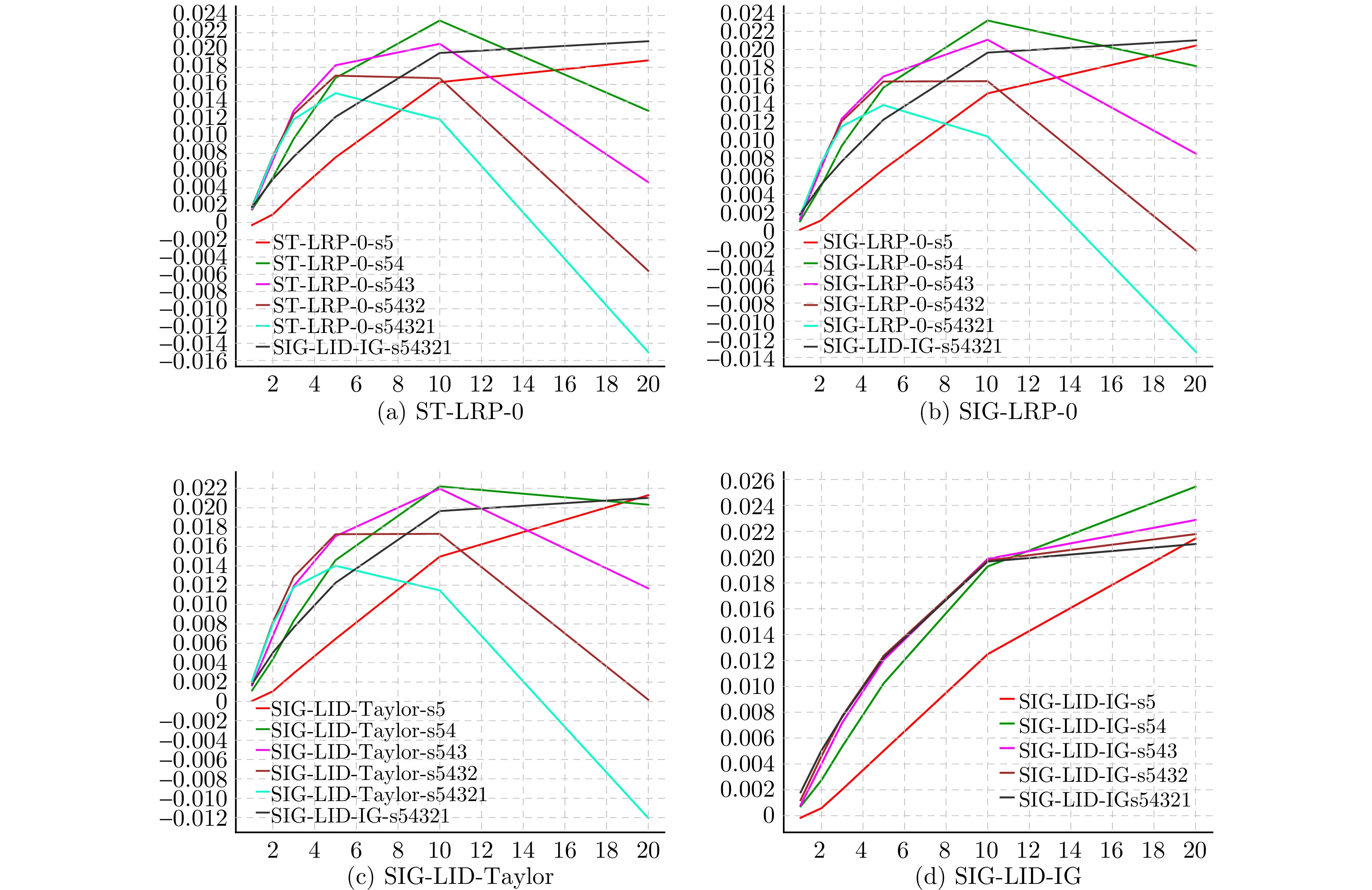
方法名 相关性计算规则 LRP-0 $R(Y^{l-1} )=\frac{R(Y^l)}{Y^l}\odot W^l\odot Y^{l-1}$ DeepLIFT $R(Y^{l-1} )=\frac{R(Y^l)}{\Delta Y^l}\odot W^l\odot \Delta Y^{l-1}$ LID-Taylor $R(Y^{l-1} )=\frac{R(Y^l)}{\Delta Y^l}\odot D^l\odot \Delta Y^{l-1}$ LID-IG $R(Y^{l-1} )=\frac{R(Y^l)}{\Delta Y^l}\odot \bar{D}^l\odot \Delta Y^{l-1}$
下载: 导出CSV
表 4 本文方法SIG-LID-Taylor、LID-IG、SIG-LID-IG与ScoreCAM、IG的PC实验数值比较
Table 4 Comparison of PC experimental values between the proposed methods SIG-LID-Taylor, LID-IG, SIG-LID-IG and ScoreCAM, IG
比例 IG ScoreCAM SIG-LID-Taylor LID-IG SIG-LID-IG 0.1 −0.010 06 −0.025 44 0.010 88 −0.015 03 0.012 43 0.2 −0.032 59 −0.037 00 −0.017 05 −0.029 54 0.000 25 0.3 −0.053 58 −0.051 20 −0.047 14 −0.044 54 −0.017 88 0.4 −0.075 42 −0.068 61 −0.078 46 −0.064 28 −0.041 39 0.5 −0.105 52 −0.092 72 −0.113 35 −0.090 19 −0.071 76 0.6 −0.148 30 −0.131 05 −0.160 32 −0.133 97 −0.115 59 0.7 −0.212 55 −0.193 31 −0.222 92 −0.200 09 −0.185 15 0.8 −0.308 24 −0.287 81 −0.321 89 −0.298 01 −0.287 73 0.9 −0.456 71 −0.436 46 −0.465 28 −0.449 57 −0.444 88
下载: 导出CSV
-
[1] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6): 84−90 doi: 10.1145/3065386 [2] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. In: Proceedings of the 3rd International Conference on Learning Representations. San Diego, USA: ICLR, 2014. 1−14 [3] Szegedy C, Liu W, Jia Y Q, Sermanet P, Reed S, Anguelov D, et al. Going deeper with convolutions. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 1−9 [4] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 770−778 [5] Girshick R, Donahue J, Darrell T, Malik J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(1): 142−158 doi: 10.1109/TPAMI.2015.2437384 [6] Girshick R. Fast R-CNN. In: Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 1440−1448 [7] Szegedy C, Zaremba W, Sutskever I, Bruna J, Erhan D, Goodfellow I J, et al. Intriguing properties of neural networks. In: Proceedings of the 2nd International Conference on Learning Representations. Banff, Canada: ICLR, 2014. [8] Zeiler M D, Fergus R. Visualizing and understanding convolutional networks. In: Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014. 818−833 [9] Erhan D, Bengio Y, Courville A, Vincent P. Visualizing Higher-layer Features of a Deep Network, Technical Report 1341, University of Montreal, Canada, 2009. [10] Zhou B L, Khosla A, Lapedriza A, Oliva A, Torralba A. Learning deep features for discriminative localization. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 2921−2929 [11] Selvaraju R R, Cogswell M, Das A, Vedantam R, Parikh D, Batra D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In: Proceedings of the IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017. 618−626 [12] Jiang P T, Zhang C B, Hou Q B, Cheng M M, Wei Y C. LayerCAM: Exploring hierarchical class activation maps for localization. IEEE Transactions on Image Processing, 2021, 30: 5875−5888 doi: 10.1109/TIP.2021.3089943 [13] Wang H F, Wang Z F, Du M N, Yang F, Zhang Z J, Ding S R, et al. Score-CAM: Score-weighted visual explanations for convolutional neural networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Seattle, USA: IEEE, 2020. 111−119 [14] Bach S, Binder A, Montavon G, Klauschen F, Müller K R, Samek W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One, 2015, 10(7): Article No. e0130140 doi: 10.1371/journal.pone.0130140 [15] Montavon G, Binder A, Lapuschkin S, Samek W, Müller K R. Layer-wise relevance propagation: An overview. Explainable AI: Interpreting, Explaining and Visualizing Deep Learning. Cham: Springer, 2019. 193−209 [16] Samek W, Montavon G, Lapuschkin S, AndersC J, Müller K R. Explaining deep neural networks and beyond: A review of methods and applications. Proceedings of the IEEE, 2021, 109(3): 247−278 doi: 10.1109/JPROC.2021.3060483 [17] Montavon G, Samek W, Müller K R. Methods for interpreting and understanding deep neural networks. Digital Signal Processing, 2018, 73: 1−15 doi: 10.1016/j.dsp.2017.10.011 [18] Montavon G, Lapuschkin S, Binder A, Samek W, Müller K R. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognition, 2017, 65: 211−222 doi: 10.1016/j.patcog.2016.11.008 [19] Gu J D, Yang Y C, Tresp V. Understanding individual decisions of CNNs via contrastive backpropagation. In: Proceedings of the 14th Asian Conference on Computer Vision. Perth, Australia: Springer, 2018. 119−134 [20] Iwana B K, Kuroki R, Uchida S. Explaining convolutional neural networks using softmax gradient layer-wise relevance propagation. In: Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop. Seoul, Korea (South): IEEE, 2019. 4176−4185 [21] Sundararajan M, Taly A, Yan Q Q. Axiomatic attribution for deep networks. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: PMLR, 2017. 3319−3328 [22] Lundberg S M, Lee S I. A unified approach to interpreting model predictions. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 4768−4777 [23] Shrikumar A, Greenside P, Kundaje A. Learning important features through propagating activation differences. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: PMLR, 2017. 3145−3153 [24] Colley S J. Vector Calculus (Fourth edition). Boston: Pearson, 2011. -
计量
- 文章访问数: 238
- HTML全文浏览量: 80
- PDF下载量: 57
- 被引次数: 0
