-
摘要: Schnakenberg系统是一类典型的化学反应扩散控制系统. 目前国内外研究仅局限于Schnakenberg系统的Turing不稳定与分岔, 而关于其化学斑图演化机理的报道较少. 斑图机理分析可以准确揭示化学反应中自组织现象的产生和空间模式的演化规律. 本文研究交叉扩散驱动下Schnakenberg系统斑图的结构蜕变、演化速度及时间依赖性, 重点探讨交叉扩散对其动力学与斑图演化的响应机制. 研究发现, 当自扩散诱导的系统稳定时, 交叉扩散可以激发斑图的产生; 当自扩散诱导的系统不稳定时, 交叉扩散可以实现斑图结构的蜕变; 对于环波结构, 不同组分的交叉扩散可以影响其演化速度; 对于时间依赖性, 交叉扩散可以激发随时间周期变化的斑图产生, 并可将此类斑图转换为随时间相对稳定的斑图. 因此, 交叉扩散对于Schnakenberg系统的斑图产生、蜕变、演化速度及时间依赖性都起着至关重要的作用.
-
关键词:
- 交叉扩散 /
- Schnakenberg系统 /
- 时空斑图 /
- 稳定性 /
- 环波
Abstract: Schnakenberg system is a typical chemical reaction-diffusion control system. Currently, research both domestically and internationally is limited to Turing instability and bifurcation of such system, with relatively fewer reports on the evolution mechanism of its chemical patterns. Pattern mechanism analysis can accurately reveal the generation of self-organization phenomena and the evolution of spatial patterns in chemical reactions. This paper investigates the structural transformation, evolution speed, and time-dependence of patterns of Schnakenberg system under cross-diffusion driving, and focuses on exploring the response mechanism of cross-diffusion to its kinetics and pattern evolution. The findings indicate that when a system induced by self-diffusion is stable, cross-diffusion can trigger pattern formation. When a system induced by self-diffusion is unstable, cross-diffusion can lead to the transformation of pattern structures. For circular wave structures, different components of cross-diffusion can influence their evolution speed. In the context of temporal dependence, cross-diffusion can trigger the generation of patterns that vary periodically with time and can transform such patterns into relatively stable ones over time. Therefore, cross-diffusion plays a crucial role in the pattern generation, transformation, evolution speed, and temporal dependence of Schnakenberg system.-
Key words:
- Cross-diffusion /
- Schnakenberg system /
- spatiotemporal patterns /
- stability /
- circular wave
-
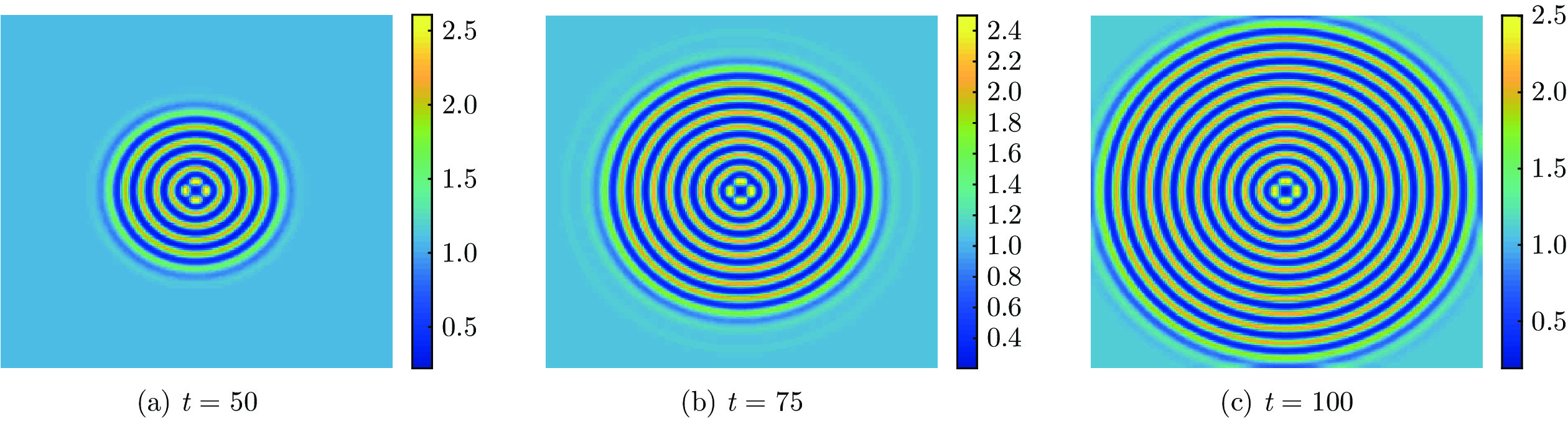
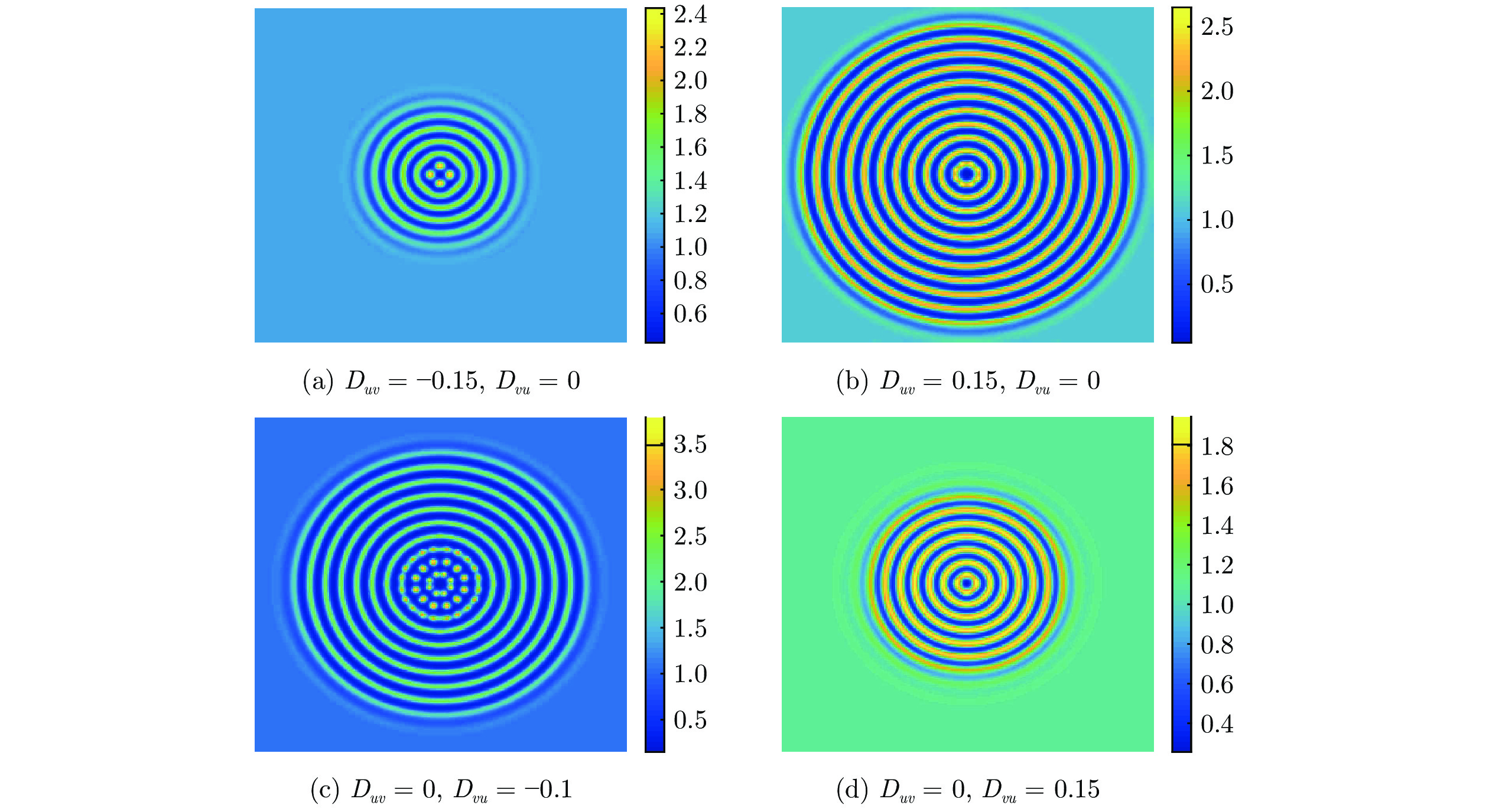
表 1 不同交叉扩散系数取值的12环成型时间$(a = 0.1$, $b = 1.0$, $D_u = 0.1$, $D_v = 2.0)$
Table 1 Formation times of 12-ring patterns with different cross-diffusion coefficient values $(a = 0.1$, $b = 1.0$, $D_u = 0.1$, $D_v = 2.0)$
$D_{uv}$ $D_{vu}$ $t=75$ 时环数 12环成型时间 0 0 9 100 −0.15 0 6 155 0.15 0 11 85 0 −0.10 10 95 0 0.15 7 125 -
[1] Turing A M. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society B: Biological Sciences, 1952, 237(641): 37−72 [2] Page K M, Maini P K, Monk N A M. Complex pattern formation in reaction-diffusion systems with spatially varying parameters. Physica D: Nonlinear Phenomena, 2005, 202(1−2): 95−115 doi: 10.1016/j.physd.2005.01.022 [3] 齐洁, 齐金鹏. 具有对称初始数据的二维反应扩散方程的边界镇定. 自动化学报, 2015, 41(1): 209−214Qi Jie, Qi Jin-Peng. Boundary stabilization for a 2-D reaction-diffusion equation with symmetrical initial data. Acta Automatica Sinica, 2015, 41(1): 209−214 [4] 齐洁, 王川, 潘峰. 球对称n维反应扩散方程的边界观测与输出反馈控制. 自动化学报, 2015, 41(7): 1356−1364Qi Jie, Wang Chuan, Pan Feng. Boundary observer and output-feedback control for a class of n-dimensional symmetric advection-diffusion equations. Acta Automatica Sinica, 2015, 41(7): 1356−1364 [5] 庄波, 崔宝同, 楼旭阳, 陈娟. 基于反步法的耦合分数阶反应扩散系统边界输出反馈控制. 自动化学报, 2022, 48(11): 2729−2743Zhuang Bo, Cui Bao-Tong, Lou Xu-Yang, Chen Juan. Backstepping-based output feedback boundary control for coupled fractional reaction-diffusion systems. Acta Automatica Sinica, 2022, 48(11): 2729−2743 [6] Du L L. Blow-up for a degenerate reaction-diffusion system with nonlinear nonlocal sources. Journal of Computational and Applied Mathematics, 2007, 202(2): 237−247 doi: 10.1016/j.cam.2006.02.028 [7] Yang R. Cross-diffusion induced spatiotemporal patterns in Schnakenberg reaction-diffusion model. Nonlinear Dynamics, 2022, 110(2): 1753−1766 doi: 10.1007/s11071-022-07691-1 [8] Lu Y X, Xiao M, Huang C D, Cheng Z S, Wang Z X, Cao J D. Early warning of tipping in a chemical model with cross-diffusion via spatiotemporal pattern formation and transition. Chaos, 2023, 33(7): Article No. 073120 doi: 10.1063/5.0152241 [9] Al Saadi F, Champneys A. Unified framework for localized patterns in reaction-diffusion systems; the Gray-Scott and Gierer-Meinhardt cases. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2021, 379(2213): Article No. 20200277 doi: 10.1098/rsta.2020.0277 [10] 黄曙磬, 程代展. 微分几何方法及其在化学反应器控制中的应用. 自动化学报, 1988, 14(5): 329−336Huang Shu-Qing, Cheng Dai-Zhan. Differential geometric method and its application in chemical reactor control. Acta Automatica Sinica, 1988, 14(5): 329−336 [11] 吴坚刚, 刘仁华, 张素贞. 乙苯脱氢反应器系统的广义预测控制. 自动化学报, 1991, 17(2): 174−181Wu Jian-Gang, Liu Ren-Hua, Zhang Su-Zhen. Generalized predictive control of ethylbenzene dehydrogenation reactor system. Acta Automatica Sinica, 1991, 17(2): 174−181 [12] Ghosh M K, Sardar T, Cao X B, Roy P K. Mathematical study of a memory induced biochemical system. IEEE/CAA Journal of Automatica Sinica, 2018, 5(6): 1142−1149 doi: 10.1109/JAS.2018.7511234 [13] Schnakenberg J. Simple chemical reaction systems with limit cycle behaviour. Journal of Theoretical Biology, 1979, 81(3): 389−400 doi: 10.1016/0022-5193(79)90042-0 [14] Ishii Y. Stability of multi-peak symmetric stationary solutions for the Schnakenberg model with periodic heterogeneity. Communications on Pure and Applied Analysis, 2020, 19(6): 2965−3031 doi: 10.3934/cpaa.2020130 [15] Doelman A, Kaper T J. Semistrong pulse interactions in a class of coupled reaction-diffusion equations. SIAM Journal on Applied Dynamical Systems, 2003, 2(1): 53−96 doi: 10.1137/S1111111102405719 [16] Iron D, Wei J C, Winter M. Stability analysis of Turing patterns generated by the Schnakenberg model. Journal of Mathematical Biology, 2004, 49(4): 358−390 doi: 10.1007/s00285-003-0258-y [17] Gomez D, Mei L F, Wei J C. Stable and unstable periodic spiky solutions for the Gray-Scott system and the Schnakenberg system. Journal of Dynamics and Differential Equations, 2020, 32(1): 441−481 doi: 10.1007/s10884-019-09736-3 [18] Ishii Y, Kurata K. Existence of multi-peak solutions to the Schnakenberg model with heterogeneity on metric graphs. Communications on Pure and Applied Analysis, 2021, 20(4): 1633−1679 doi: 10.3934/cpaa.2021035 [19] Ishii Y. The effect of heterogeneity on one-peak stationary solutions to the Schnakenberg model. Journal of Differential Equations, 2021, 285: 321−382 doi: 10.1016/j.jde.2021.03.007 [20] Ishii Y, Kurata K. Existence and stability of one-peak symmetric stationary solutions for the Schnakenberg model with heterogeneity. Discrete and Continuous Dynamical Systems, 2019, 39(5): 2807−2875 doi: 10.3934/dcds.2019118 [21] Al Noufaey K S. Semi-analytical solutions of the Schnakenberg model of a reaction-diffusion cell with feedback. Results in Physics, 2018, 9: 609−614 doi: 10.1016/j.rinp.2018.03.017 [22] Kaper H G, Wang S H, Yari M. Dynamical transitions of Turing patterns. Nonlinearity, 2009, 22(3): 601−626 doi: 10.1088/0951-7715/22/3/006 [23] Xu C, Wei J J. Hopf bifurcation analysis in a one-dimensional Schnakenberg reaction-diffusion model. Nonlinear Analysis: Real World Applications, 2012, 13(4): 1961−1977 doi: 10.1016/j.nonrwa.2012.01.001 [24] Jiang W H, Wang H B, Cao X. Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay. Journal of Dynamics and Differential Equations, 2019, 31(4): 2223−2247 doi: 10.1007/s10884-018-9702-y [25] Garzón-Alvarado D A, García-Aznar J M, Doblaré M. A reaction-diffusion model for long bones growth. Biomechanics and Modeling in Mechanobiology, 2009, 8(5): 381−395 doi: 10.1007/s10237-008-0144-z [26] Liu P, Shi J P, Wang Y W, Feng X H. Bifurcation analysis of reaction-diffusion Schnakenberg model. Journal of Mathematical Chemistry, 2013, 51(8): 2001−2019 doi: 10.1007/s10910-013-0196-x [27] Chaplain M A J, Ganesh M, Graham I G. Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumour growth. Journal of Mathematical Biology, 2001, 42(5): 387−423 doi: 10.1007/s002850000067 [28] Ricard M R, Mischler S. Turing instabilities at Hopf bifurcation. Journal of Nonlinear Science, 2009, 19(5): 467−496 doi: 10.1007/s00332-009-9041-6 [29] Fragnelli G, Mugnai D. Turing patterns for a coupled two-cell generalized Schnakenberg model. Complex Variables and Elliptic Equations, 2020, 65(8): 1343−1359 doi: 10.1080/17476933.2019.1631291 [30] Khudhair H K, Zhang Y Z, Fukawa N. Pattern selection in the Schnakenberg equations: From normal to anomalous diffusion. Numerical Methods for Partial Differential Equations, 2022, 38(6): 1843−1860 doi: 10.1002/num.22842 [31] Liu G Q, Wang Y W. Pattern formation of a coupled two-cell Schnakenberg model. Discrete and Continuous Dynamical Systems-S, 2017, 10(5): 1051−1062 doi: 10.3934/dcdss.2017056 [32] Wong T, Ward M J. Spot patterns in the 2-D Schnakenberg model with localized heterogeneities. Studies in Applied Mathematics, 2021, 146(4): 779−833 doi: 10.1111/sapm.12361 [33] Maini P K, Woolley T E, Baker R E, Gaffney E A, Lee S S. Turing's model for biological pattern formation and the robustness problem. Interface Focus, 2012, 2(4): 487−496 doi: 10.1098/rsfs.2011.0113 [34] Kerner E H. A statistical mechanics of interacting biological species. The Bulletin of Mathematical Biophysics, 1957, 19(2): 121−146 doi: 10.1007/BF02477883 [35] Sherratt J A. Wavefront propagation in a competition equation with a new motility term modelling contact inhibition between cell populations. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2000, 456(2002): 2365−2386 doi: 10.1098/rspa.2000.0616 [36] Galiano G. On a cross-diffusion population model deduced from mutation and splitting of a single species. Computers & Mathematics With Applications, 2012, 64(6): 1927−1936 [37] Yizhaq H, Portnov B A, Meron E. A mathematical model of segregation patterns in residential neighbourhoods. Environment and Planning A: Economy and Space, 2004, 36(1): 149−172 doi: 10.1068/a35274 [38] Vanag V K, Epstein I R. Cross-diffusion and pattern formation in reaction-diffusion systems. Physical Chemistry Chemical Phy sics, 2009, 11(6): 897−912 doi: 10.1039/B813825G [39] De Decker Y, Marbach H, Hinz M, Günther S, Kiskinova M, Mikhailov A S, et al. Promoter-induced reactive phase separation in surface reactions. Physical Review Letters, 2004, 92(19): Article No. 198305 doi: 10.1103/PhysRevLett.92.198305 [40] Vanag V K, Rossi F, Cherkashin A, Epstein I R. Cross-diffusion in a water-in-oil microemulsion loaded with malonic acid or ferroin. Taylor dispersion method for four-component systems. The Journal of Physical Chemistry B, 2008, 112(30): 9058−9070 doi: 10.1021/jp800525w [41] Currò C, Valenti G. Subcritical Turing patterns in hyperbolic models with cross-diffusion. Ricerche di Matematica, 2021, 71(1): 147−167 [42] Madzvamuse A, Ndakwo H S, Barreira R. Cross-diffusion-driven instability for reaction-diffusion systems: Analysis and simulations. Journal of Mathematical Biology, 2015, 70(4): 709−743 doi: 10.1007/s00285-014-0779-6 [43] Miller D G. Some comments on multicomponent diffusion: Negative main term diffusion coefficients, second law constraints, solvent choices, and reference frame transformations. The Journal of Physical Chemistry, 1986, 90(8): 1509−1519 doi: 10.1021/j100399a010 -




 下载:
下载: