-
摘要: 近年来, 人工智能(Artificial intelligence, AI)技术在棋牌游戏、计算机视觉、自然语言处理和蛋白质结构解析与预测等研究领域取得了众多突破性进展, 传统学科之间的固有壁垒正在被逐步打破, 多学科深度交叉融合的态势变得越发明显. 作为现代智能科学的三个重要组成部分, 博弈论、多智能体学习与控制论自诞生之初就逐渐展现出一种“你中有我, 我中有你” 的关联关系. 特别地, 近年来在AI技术的促进作用下, 这三者间的交叉研究成果正呈现出一种井喷式增长的态势. 为及时反映这一学术动态和趋势, 本文对这三者的异同、联系以及最新的研究进展进行了系统梳理. 首先, 介绍了作为纽带连接这三者的四种基本博弈形式, 进而论述了对应于这四种基本博弈形式的多智能体学习方法; 然后, 按照不同的专题, 梳理了这三者交叉研究的最新进展; 最后, 对这一新兴交叉研究领域进行了总结与展望.Abstract: In recent years, along with some ground-breaking advances made by artificial intelligence (AI) in Go, chess, video games, computer vision, natural language processing, and the analysis and prediction of protein structures, the inherent barriers of traditional disciplines are gradually being broken, and a cross-discipline wave is steadily underway in academia. As three important components of modern intelligent science, game theory, multi-agent learning, and control theory have witnessed a closely interrelated relationship from the very beginning of their establishments. Especially, with the aid of the great development of AI technologies in recent years, their interactions are becoming closer and closer, and the relevant interdisciplinary research is showing a blowout growth. To reflect this trend, in this paper, we provide a comprehensive survey of the connections, distinctions, and latest interdisciplinary research progress of games, multi-agent learning, and control. Specifically, we first introduce four different types of games, which are normally used to connect these three fields. Then, corresponding to these four types of games, some multi-agent learning methods are reviewed. Subsequently, following different research topics, we survey the latest interdisciplinary research progress of games, learning, and control. Finally, we provide a summary and an outlook for this emerging interdisciplinary field.
-
Key words:
- Game theory /
- multi-agent learning /
- control theory /
- reinforcement learning /
- artificial intelligence
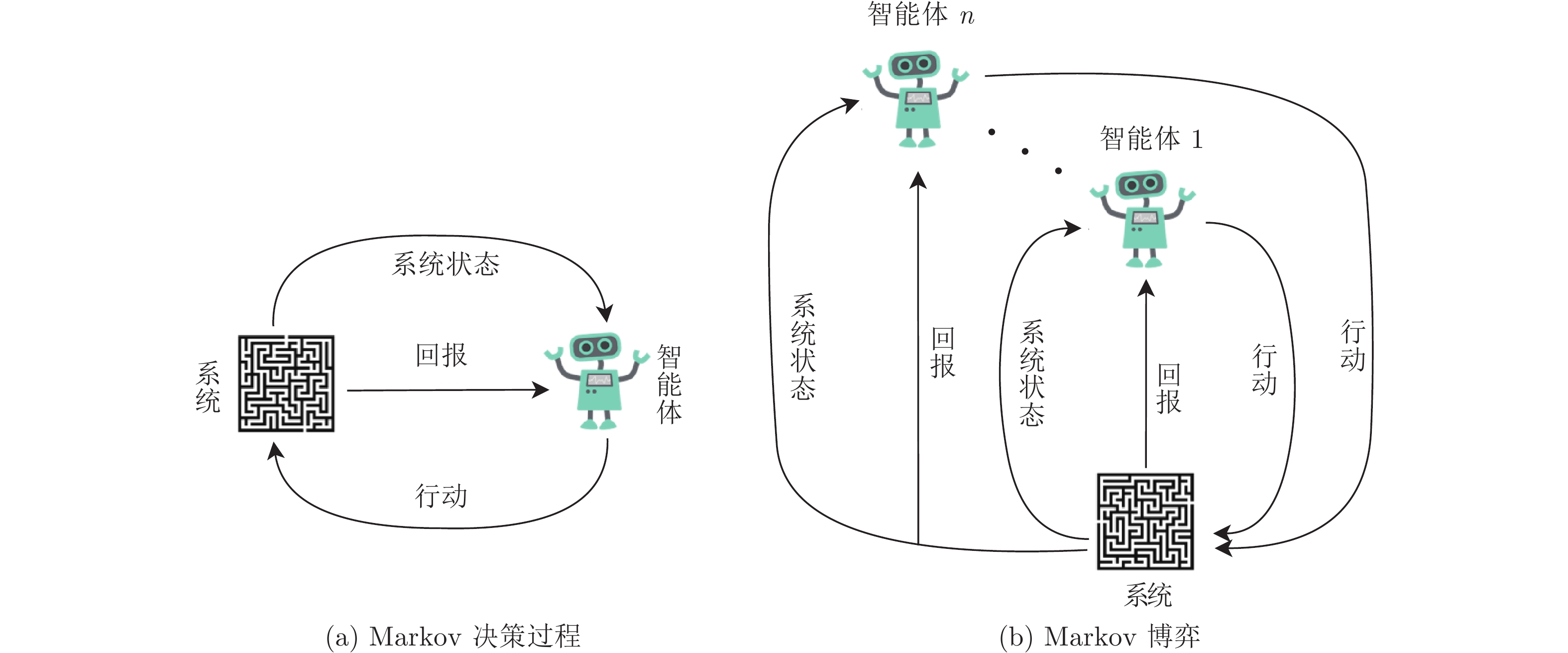
1) 1 在本文中, 智能体也称为博弈者(Player)或决策者(Decision-maker).2) 2 在理性人的假设下, 博弈者最大化收益函数等价于最小化成本函数.3) 3 期刊Artificial Intelligence在2007年组织的一个关于博弈论与多智能体学习的专刊中, 专门对Nash均衡在现实应用中的局限性进行了讨论[44, 62]. 另外, 文献[63−64]从实证等角度对Nash均衡进行了重新审视并提出了一些可能的替代概念.5) 5 除非特别说明, 本文只讨论$ \Gamma $ 为离散无穷的情况, 即随机博弈在离散时间集上进行无穷轮.6 随机博弈中所说的“策略” (Policy)与演化博弈中所说的“策略” (Strategy)不是完全等同的概念. 在随机博弈中, 博弈者的策略是指行动集(或纯策略集)上的一个概率分布(也称为混合策略); 而在演化博弈中, 个体的策略通常隐含地假定是一个确定性的纯策略. 因此, 演化博弈中所说的策略实质上是等同于随机博弈中的某一个具体的行动(或纯策略). 另外, 为了叙述方便, 本文只讨论确定性的策略; 而对于随机性的策略$ \pi_i(\cdot|s): {\cal{S}}\rightarrow \Delta({\cal{A}}_i) $ ,$ \forall i\in{\cal{N}} $ , 本文中的相关结果可类似地得到.6) 随机博弈中所说的“策略” (Policy)与演化博弈中所说的“策略” (Strategy)不是完全等同的概念. 在随机博弈中, 博弈者的策略是指行动集(或纯策略集)上的一个概率分布(也称为混合策略); 而在演化博弈中, 个体的策略通常隐含地假定是一个确定性的纯策略. 因此, 演化博弈中所说的策略实质上是等同于随机博弈中的某一个具体的行动(或纯策略). 另外, 为了叙述方便, 本文只讨论确定性的策略; 而对于随机性的策略$ \pi_i(\cdot|s): {\cal{S}}\rightarrow \Delta({\cal{A}}_i) $ ,$ \forall i\in{\cal{N}} $ , 本文中的相关结果可类似地得到.7) 7 文献[169]也对其他形式的计算方式进行了分析和讨论.8$ \gamma $ 的另外一种解释是: 在一轮博弈结束之后, 下一轮博弈继续进行的概率.8)$ \gamma $ 的另外一种解释是: 在一轮博弈结束之后, 下一轮博弈继续进行的概率.10) 10 从控制论的角度上讲, Markov决策过程中的智能体一般被视为是控制器, 而“系统” (或“环境”)则被视为是受控对象. 因此, Markov决策过程也称为“受控Markov过程”[209].11) 11 文献[197]将目前的强化学习方法划分为表格解方法(Tabular solution method)和近似解方法(Approximate solution method).12 在强化学习算法中, 函数$ r(\cdot) $ 的具体形式并不需要明确的已知, 它的某一个取值$ r(s, a, s') $ 是系统(或环境)反馈给智能体的, 并且智能体并不知道$ r(\cdot) $ 的具体形式. 为了行文简洁, 本文并没有在符号形式上突出这一点.12) 在强化学习算法中, 函数$ r(\cdot) $ 的具体形式并不需要明确的已知, 它的某一个取值$ r(s, a, s') $ 是系统(或环境)反馈给智能体的, 并且智能体并不知道$ r(\cdot) $ 的具体形式. 为了行文简洁, 本文并没有在符号形式上突出这一点.13) 13 本文这部分主要专注介绍鲁棒强化学习, 未涉及鲁棒学习中的诸如鲁棒深度学习等其他内容.14) 14 除非特别说明, 本节中的符号$ t $ 专指连续时间, 而不再表示博弈进行的轮次.15) 15 文献[305]也证明了非遍历情况下该平稳分布的存在性. -
表 1 几类典型的两人两策略对称博弈
Table 1 Some representative examples of two-player two-strategy symmetric games
博弈类型 收益值大小关系 博弈类型 收益值大小关系 囚徒困境 (Prisoner's dilemma) $\left\{\begin{aligned} &{\mathfrak{a}}_{21} > {\mathfrak{a}}_{11} > {\mathfrak{a}}_{22} > {\mathfrak{a}}_{12}\\ & 2{\mathfrak{a}}_{11} > {\mathfrak{a}}_{12}+{\mathfrak{a}}_{21} \end{aligned}\right.$ 和谐博弈 (Harmony game) ${\mathfrak{a}}_{11} > {\mathfrak{a}}_{21}, {\mathfrak{a}}_{12} > {\mathfrak{a}}_{22}$ 雪堆博弈 (Snowdrift game) ${\mathfrak{a}}_{21} > {\mathfrak{a}}_{11},\ {\mathfrak{a}}_{12} > {\mathfrak{a}}_{22}$ 猎鹿博弈 (Stag-hunt game) $\mathfrak{a}_{11}>\mathfrak{a}_{21},\ \mathfrak{a}_{22}>\mathfrak{a}_{12}$ 表 2
$d$ 人随机博弈的收益表Table 2 The payoff table of d-player stochastic games
$d-1$个共同博弈者中行动为 C 的博弈者个数 $d-1$ ··· $\jmath$ ··· $0$ 行动为 C 的博弈者的收益 ${\mathfrak{a}}_{d-1}(s)$ ··· ${\mathfrak{a}}_{\jmath}(s)$ ··· ${\mathfrak{a}}_0(s)$ 行动为 D 的博弈者的收益 ${\mathfrak{b}}_{d-1}(s)$ ··· ${\mathfrak{b}}_{\jmath}(s)$ ··· ${\mathfrak {b}}_0(s)$ -
[1] McDonald K R, Pearson J M. Cognitive bots and algorithmic humans: Toward a shared understanding of social intelligence. Current Opinion in Behavioral Sciences, 2019, 29: 55-62 doi: 10.1016/j.cobeha.2019.04.013 [2] Silver D, Singh S, Precup D, Sutton R S. Reward is enough. Artificial Intelligence, 2021, 299: 103535 [3] Rahwan I, Cebrian M, Obradovich N, Bongard J, Bonnefon J F, Breazeal C, et al. Machine behaviour. Nature, 2019, 568(7753): 477-486 doi: 10.1038/s41586-019-1138-y [4] Dafoe A, Bachrach Y, Hadfield G, Horvitz E, Larson K, Graepel T. Cooperative AI: Machines must learn to find common ground. Nature, 2021, 593(7857): 33-36 doi: 10.1038/d41586-021-01170-0 [5] Russell S, Dewey D, Tegmark M. Research priorities for robust and beneficial artificial intelligence. AI Magazine, 2015, 36(4): 105-114 doi: 10.1609/aimag.v36i4.2577 [6] Amodei D, Olah C, Steinhardt J, Christiano P, Schulman J, Mané D. Concrete problems in AI safety. arXiv: 1606.06565, 2016. [7] Bonnefon J F, Shariff A, Rahwan I. The social dilemma of autonomous vehicles. Science, 2016, 352(6293): 1573-1576 doi: 10.1126/science.aaf2654 [8] Jobin A, Ienca M, Vayena E. The global landscape of AI ethics guidelines. Nature Machine Intelligence, 2019, 1(9): 389-399 doi: 10.1038/s42256-019-0088-2 [9] Myerson R B. Game Theory: Analysis of Conflict. Cambridge, USA: Harvard University Press, 1997. [10] von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton, USA: Princeton University Press, 1944. [11] Wooldridge M, Jennings N R. Intelligent agents: Theory and practice. The Knowledge Engineering Review, 1995, 10(2): 115-152 doi: 10.1017/S0269888900008122 [12] Sen S. Multiagent systems: Milestones and new horizons. Trends in Cognitive Sciences, 1997, 1(9): 334-340 doi: 10.1016/S1364-6613(97)01100-5 [13] Weiss G. Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence. Cambridge, USA: MIT Press, 1999. [14] Brown G W. Iterative solution of games by fictitious play. In: T.C. Koopmans, editor, Activity Analysis of Production and Allocation. New York: Wiley, 1951. 374–376 [15] Tuyls K, Weiss G. Multiagent learning: Basics, challenges, and prospects. AI Magazine, 2012, 33(3): Article No. 41 doi: 10.1609/aimag.v33i3.2426 [16] Moravčík M, Schmid M, Burch N, Lisý V, Morrill D, Bard N, et al. DeepStack: Expert-level artificial intelligence in heads-up no-limit poker. Science, 2017, 356(6337): 508-513 doi: 10.1126/science.aam6960 [17] Brown N, Sandholm T. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals. Science, 2018, 359(6374): 418-424 doi: 10.1126/science.aao1733 [18] Brown N, Sandholm T. Superhuman AI for multiplayer poker. Science, 2019, 365(6456): 885-890 doi: 10.1126/science.aay2400 [19] Vinyals O, Babuschkin I, Czarnecki W M, Mathieu M, Dudzik A, Chung J, et al. Grandmaster level in StarCraft Ⅱ using multi-agent reinforcement learning. Nature, 2019, 575(7782): 350-354 doi: 10.1038/s41586-019-1724-z [20] Jaderberg M, Czarnecki W M, Dunning I, Marris L, Lever G, Castañeda A G, et al. Human-level performance in 3D multiplayer games with population-based reinforcement learning. Science, 2019, 364(6443): 859-865 doi: 10.1126/science.aau6249 [21] Wurman P R, Barrett S, Kawamoto Kenta, MacGlashan J, Subramanian K, Walsh T J, et al. Outracing champion Gran Turismo drivers with deep reinforcement learning. Nature, 2022, 602(7896): 223-228 doi: 10.1038/s41586-021-04357-7 [22] Bennett S. A brief history of automatic control. IEEE Control Systems Magazine, 1996, 16(3): 17-25 doi: 10.1109/37.506394 [23] Wiener N. Cybernetics or Control and Communication in the Animal and the Machine. Cambridge, USA: MIT Press, 1948. [24] 郭雷. 不确定性动态系统的估计、控制与博弈. 中国科学: 信息科学, 2020, 50(9): 1327-1344 doi: 10.1360/SSI-2020-0277Guo Lei. Estimation, control, and games of dynamical systems with uncertainty. Scientia Sinica Informationis, 2020, 50(9): 1327-1344 doi: 10.1360/SSI-2020-0277 [25] Marschak J. Elements for a theory of teams. Management Science, 1955, 1(2): 127-137 doi: 10.1287/mnsc.1.2.127 [26] Ho Y C. Team decision theory and information structures in optimal control problems—Part I. IEEE Transactions on Automatic Control, 1972, 17(1): 15−22 doi: 10.1109/TAC.1972.1099850 [27] Boutilier C. Planning, learning and coordination in multiagent decision processes. In: Proceedings of the 6th Conference on Theoretical Aspects of Rationality and Knowledge. De Zeeuwse Stromen, The Netherlands: Morgan Kaufmann Publishers Inc, 1996. 195−210 [28] Wang X F, Sandholm T. Reinforcement learning to play an optimal Nash equilibrium in team Markov games. In: Proceedings of the 15th International Conference on Neural Information Processing Systems. Vancouver, Canada: MIT Press, 2002. 1603−1610 [29] Witsenhausen H S. A counterexample in stochastic optimum control. SIAM Journal on Control, 1968, 6(1): 131-147 doi: 10.1137/0306011 [30] Marden J R, Shamma J S. Game theory and control. Annual Review of Control, Robotics, and Autonomous Systems, 2018, 1: 105-134 doi: 10.1146/annurev-control-060117-105102 [31] Lewis F L, Zhang H W, Hengster-Movric K, Das A. Cooperative Control of Multi-Agent Systems: Optimal and Adaptive Design Approaches. New York, USA: Springer, 2013. [32] Bauso D, Pesenti R. Team theory and person-by-person optimization with binary decisions. SIAM Journal on Control and Optimization, 2012, 50(5): 3011-3028 doi: 10.1137/090769533 [33] Nayyar A, Teneketzis D. Common knowledge and sequential team problems. IEEE Transactions on Automatic Control, 2019, 64(12): 5108-5115 doi: 10.1109/TAC.2019.2912536 [34] Yongacoglu B, Arslan G, Yüksel S. Decentralized learning for optimality in stochastic dynamic teams and games with local control and global state information. IEEE Transactions on Automatic Control, 2022, 67(10): 5230-5245 doi: 10.1109/TAC.2021.3121228 [35] Littman M L. Markov games as a framework for multi-agent reinforcement learning. In: Proceedings of the 11th International Conference on Machine Learning. New Brunswick, USA: Morgan Kaufmann Publishers Inc, 1994. 157−163 [36] Başar T, Bernhard P. H∞ Optimal Control and Related Minimax Design Problems: A Dynamic Game Approach (Second edition). New York: Springer, 2008. [37] Başar T, Olsder G J. Dynamic Noncooperative Game Theory (Second edition). Philadelphia: SIAM, 1998. [38] Nash Jr J F. Equilibrium points in n-person games. Proceedings of the National Academy of Sciences of the United States of America, 1950, 36(1): 48-49 doi: 10.1073/pnas.36.1.48 [39] Hu J L, Wellman M P. Nash Q-learning for general-sum stochastic games. Journal of Machine Learning Research, 2003, 4: 1039-1069 [40] Lowe R, Wu Y, Tamar A, Harb J, Abbeel P, Mordatch I. Multi-agent actor-critic for mixed cooperative-competitive environments. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc, 2017. 6382−6393 [41] Li N, Marden J R. Designing games for distributed optimization. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(2): 230-242 doi: 10.1109/JSTSP.2013.2246511 [42] 钱学森 [著], 戴汝为 [译]. 工程控制论. 北京: 科学出版社, 1958.Tsien Hsue-Shen. Engineering Cybernetics. New York: McGraw Hill Book, 1954 [43] Lamnabhi-Lagarrigue F, Annaswamy A, Engell S, Isaksson A, Khargonekar P, Murray R M, et al. Systems & control for the future of humanity, research agenda: Current and future roles, impact and grand challenges. Annual Reviews in Control, 2017, 43: 1-64 doi: 10.1016/j.arcontrol.2017.04.001 [44] Shoham Y, Powers R, Grenager T. If multi-agent learning is the answer, what is the question? Artificial Intelligence, 2007, 171(7): 365-377 doi: 10.1016/j.artint.2006.02.006 [45] Fudenberg D, Levine D K. The Theory of Learning in Games. Cambridge, USA: MIT Press, 1998. [46] Young H P. Strategic Learning and Its Limits. Oxford: Oxford University Press, 2004. [47] Busoniu L, Babuska R, De Schutter B. A comprehensive survey of multiagent reinforcement learning. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2008, 38(2): 156-172 doi: 10.1109/TSMCC.2007.913919 [48] Nowé A, Vrancx P, De Hauwere Y M. Game theory and multi-agent reinforcement learning. In: Marco Wiering and Martijn van Otterlo, editors, Reinforcement Learning: State-of-the-Art, Berlin: Heidelberg, 2012. 441–470 [49] Zhang K Q, Yang Z R, Başar T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In: Kyriakos G. Vamvoudakis, Yan Wan, Frank L. Lewis, and Derya Cansever, editors, Handbook of reinforcement learning and control, Cham, Switzerland: Springer, 2021. 321–384 [50] Yang Y D, Wang J. An overview of multi-agent reinforcement learning from game theoretical perspective. arXiv: 2011.00583, 2021. [51] Ocampo-Martinez C, Quijano N. Game-theoretical methods in control of engineering systems: An introduction to the special issue. IEEE Control Systems Magazine, 2017, 37(1): 30-32 doi: 10.1109/MCS.2016.2621403 [52] Riehl J, Ramazi P, Cao M. A survey on the analysis and control of evolutionary matrix games. Annual Reviews in Control, 2018, 45: 87-106 doi: 10.1016/j.arcontrol.2018.04.010 [53] Zhang J F. Preface to special topic on games in control systems. National Science Review, 2020, 7(7): 1115-1115 doi: 10.1093/nsr/nwaa118 [54] Kiumarsi B, Vamvoudakis K G, Modares H, Lewis F L. Optimal and autonomous control using reinforcement learning: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(6): 2042-2062 doi: 10.1109/TNNLS.2017.2773458 [55] Buşoniu L, de Bruin T, Tolić D, Kober J, Palunko I. Reinforcement learning for control: Performance, stability, and deep approximators. Annual Reviews in Control, 2018, 46: 8-28 doi: 10.1016/j.arcontrol.2018.09.005 [56] Annaswamy A, Morari M, Pappas G J, Tomlin C, Vidal R, Zellinger M. Special issue on learning and control. IEEE Transactions on Automatic Control, 2022. [57] Giordano G. Tamer Başar [people in control]. IEEE Control Systems Magazine, 2021, 41(6): 28−33 [58] 程代展, 付世华. 博弈控制论简述. 控制理论与应用, 2018, 35(5): 588-592 doi: 10.7641/CTA.2017.60952Cheng Dai-Zhan, Fu Shi-Hua. A survey on game theoretical control. Control Theory & Applications, 2018, 35(5): 588-592 doi: 10.7641/CTA.2017.60952 [59] Fudenberg D, Tirole J. Game Theory. Cambridge, USA: MIT Press, 1991. [60] Osborne M J, Rubinstein A. A Course in Game Theory. Cambridge, USA: MIT Press, 1994. [61] Nash J. Non-cooperative games. Annals of Mathematics, 1951, 54(2): 286-295 doi: 10.2307/1969529 [62] Fudenberg D, Levine D K. An economist’s perspective on multi-agent learning. Artificial Intelligence, 2007, 171(7): 378-381 doi: 10.1016/j.artint.2006.11.006 [63] Camerer C F. Behavioral Game Theory: Experiments in Strategic Interaction. Princeton, USA: Princeton University Press, 2003. [64] Rubinstein A. Modeling Bounded Rationality. Cambridge, USA: MIT Press, 1998. [65] Williamson O E. Transaction-cost economics: The governance of contractual relations. The Journal of Law and Economics, 1979, 22(2): 233-261 doi: 10.1086/466942 [66] Smith J M, Price G R. The logic of animal conflict. Nature, 1973, 246(5427): 15-18 doi: 10.1038/246015a0 [67] Maynard Smith J. Evolution and the Theory of Games. Cambridge, UK: Cambridge University Press, 1982. [68] Mayr E. Populations, Species, and Evolution: An Abridgment of Animal Species and Evolution. Cambridge, USA: Harvard University Press, 1970. [69] Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge, USA: Cambridge University Press, 1998. [70] Sandholm W H. Population Games and Evolutionary Dynamics. Cambridge, USA: MIT Press, 2010. [71] Simon H A. A behavioral model of rational choice. The Quarterly Journal of Economics, 1955, 69(1): 99-118 doi: 10.2307/1884852 [72] Szabó G, Fáth G. Evolutionary games on graphs. Physics Reports, 2007, 446(4-6): 97-216 doi: 10.1016/j.physrep.2007.04.004 [73] Weibull J W. Evolutionary Game Theory. Cambridge, USA: MIT Press, 1995. [74] Nowak M A. Evolutionary Dynamics: Exploring the Equations of Life. Cambridge, USA: Harvard University Press, 2006. [75] Hofbauer J, Sigmund K. Evolutionary game dynamics. Bulletin of the American Mathematical Society, 2003, 40(4): 479-519 doi: 10.1090/S0273-0979-03-00988-1 [76] Taylor P D, Jonker L B. Evolutionary stable strategies and game dynamics. Mathematical Biosciences, 1978, 40(1-2): 145-156 doi: 10.1016/0025-5564(78)90077-9 [77] Schuster P, Sigmund K. Replicator dynamics. Journal of Theoretical Biology, 1983, 100(3): 533-538 doi: 10.1016/0022-5193(83)90445-9 [78] Brown G W, von Neumann J. Solutions of games by differential equations. In: H.W. Kuhn and A.W. Tucker, editors, Contributions to the Theory of Games (AM-24), Volume I. Princeton: Princeton University Press, 1950. 73–79 [79] Smith M J. The stability of a dynamic model of traffic assignment-an application of a method of Lyapunov. Transportation Science, 1984, 18(3): 245-252 doi: 10.1287/trsc.18.3.245 [80] Helbing D. A mathematical model for behavioral changes by pair interactions. In: Günter Haag, Ulrich Mueller, and Klaus G. Troitzsch, editors, Economic Evolution and Demographic Change: Formal Models in Social Sciences. Berlin, Heidelberg: Springer, 1992. 330−348 [81] Schlag K H. Why imitate, and if so, how?: A boundedly rational approach to multi-armed bandits. Journal of Economic Theory, 1998, 78(1): 130-156 doi: 10.1006/jeth.1997.2347 [82] Hofbauer J. On the occurrence of limit cycles in the Volterra-Lotka equation. Nonlinear Analysis: Theory, Methods & Applications, 1981, 5(9): 1003-1007 [83] Dugatkin L A, Reeve H K. Game Theory and Animal Behavior. New York: Oxford University Press, 2000. [84] Cross J G. A stochastic learning model of economic behavior. The Quarterly Journal of Economics, 1973, 87(2): 239-266 doi: 10.2307/1882186 [85] Watkins C J C H. Learning from Delayed Rewards [Ph.D. dissertation], King's College, UK, 1989 [86] Watkins C J C H, Dayan P. Q-learning. Machine Learning, 1992, 8(3): 279-292 [87] Börgers T, Sarin R. Learning through reinforcement and replicator dynamics. Journal of Economic Theory, 1997, 77(1): 1-14 doi: 10.1006/jeth.1997.2319 [88] Sato Y, Crutchfield J P. Coupled replicator equations for the dynamics of learning in multiagent systems. Physical Review E, 2003, 67(1): Article No. 015206(R) [89] Tuyls K, Verbeeck K, Lenaerts T. A selection-mutation model for Q-learning in multi-agent systems. In: Proceedings of the 2nd International Joint Conference on Autonomous Agents and MultiAgent Systems. Melbourne, Australia: International Foundation for Autonomous Agents and Multiagent Systems, 2003. 693−700 [90] Mnih V, Kavukcuoglu K, Silver D, Rusu A A, Veness J, Bellemare M G, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533 doi: 10.1038/nature14236 [91] Schrittwieser J, Antonoglou I, Hubert T, Simonyan K, Sifre L, Schmitt S, et al. Mastering Atari, Go, chess and shogi by planning with a learned model. Nature, 2020, 588(7839): 604-609 doi: 10.1038/s41586-020-03051-4 [92] Silver D, Huang A, Maddison C J, Guez A, Sifre L, Van Den driessche G, et al. Mastering the game of Go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489 doi: 10.1038/nature16961 [93] Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, et al. Mastering the game of Go without human knowledge. Nature, 2017, 550(7676): 354-359 doi: 10.1038/nature24270 [94] Tuyls K, Parsons S. What evolutionary game theory tells us about multiagent learning. Artificial Intelligence, 2007, 171(7): 406-416 doi: 10.1016/j.artint.2007.01.004 [95] Bloembergen D, Tuyls K, Hennes D, Kaisers M. Evolutionary dynamics of multi-agent learning: A survey. Journal of Artificial Intelligence Research, 2015, 53: 659-697 doi: 10.1613/jair.4818 [96] Mertikopoulos P, Sandholm W H. Learning in games via reinforcement and regularization. Mathematics of Operations Research, 2016, 41(4): 1297-1324 doi: 10.1287/moor.2016.0778 [97] Omidshafiei S, Tuyls K, Czarnecki W M, Santos F C, Rowland M, Connor J, et al. Navigating the landscape of multiplayer games. Nature Communications, 2020, 11(1): Article No. 5603 doi: 10.1038/s41467-020-19244-4 [98] Leonardos S, Piliouras G. Exploration-exploitation in multi-agent learning: Catastrophe theory meets game theory. Artificial Intelligence, 2022, 304: 103653 doi: 10.1016/j.artint.2021.103653 [99] Hauert C, De Monte S, Hofbauer J, Sigmund K. Replicator dynamics for optional public good games. Journal of Theoretical Biology, 2002, 218(2): 187-194 doi: 10.1006/jtbi.2002.3067 [100] Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science, 2002, 296(5570): 1129-1132 doi: 10.1126/science.1070582 [101] Pacheco J M, Santos F C, Souza M O, Skyrms B. Evolutionary dynamics of collective action in N-person stag hunt dilemmas. Proceedings of the Royal Society B: Biological Sciences, 2009, 276(1655): 315-321 doi: 10.1098/rspb.2008.1126 [102] Wang J, Fu F, Wu T, Wang L. Emergence of social cooperation in threshold public goods games with collective risk. Physical Review E, 2009, 80(1): Article No. 016101 [103] Souza M O, Pacheco J M, Santos F C. Evolution of cooperation under N-person snowdrift games. Journal of Theoretical Biology, 2009, 260(4): 581-588 doi: 10.1016/j.jtbi.2009.07.010 [104] Wang J, Fu F, Wang L. Effects of heterogeneous wealth distribution on public cooperation with collective risk. Physical Review E, 2010, 82(1): Article No. 016102 [105] 王龙, 丛睿, 李昆. 合作演化中的反馈机制. 中国科学: 信息科学, 2014, 44(12): 1495-1514 doi: 10.1360/N112013-00184Wang Long, Cong Rui, Li Kun. Feedback mechanism in cooperation evolving. Scientia Sinica Informationis, 2014, 44(12): 1495-1514 doi: 10.1360/N112013-00184 [106] Chen X J, Sasaki T, Brännström Å, Dieckmann U. First carrot, then stick: How the adaptive hybridization of incentives promotes cooperation. Journal of the Royal Society Interface, 2015, 12(102): Article No. 20140935 doi: 10.1098/rsif.2014.0935 [107] Huang F, Chen X J, Wang L. Conditional punishment is a double-edged sword in promoting cooperation. Scientific Reports, 2018, 8(1): Article No. 528 doi: 10.1038/s41598-017-18727-7 [108] Huang F, Chen X J, Wang L. Evolution of cooperation in a hierarchical society with corruption control. Journal of Theoretical Biology, 2018, 449: 60-72 doi: 10.1016/j.jtbi.2018.04.018 [109] Ohtsuki H, Nowak M A. The replicator equation on graphs. Journal of Theoretical Biology, 2006, 243(1): 86-97 doi: 10.1016/j.jtbi.2006.06.004 [110] Foster D, Young P. Stochastic evolutionary game dynamics. Theoretical Population Biology, 1990, 38(2): 219-232 doi: 10.1016/0040-5809(90)90011-J [111] Imhof L A. The long-run behavior of the stochastic replicator dynamics. The Annals of Applied Probability, 2005, 15(1B): 1019-1045 [112] Cressman R. Stability of the replicator equation with continuous strategy space. Mathematical Social Sciences, 2005, 50(2): 127-147 doi: 10.1016/j.mathsocsci.2005.03.001 [113] Galstyan A. Continuous strategy replicator dynamics for multi-agent Q-learning. Autonomous Agents and Multi-agent Systems, 2013, 26(1): 37-53 doi: 10.1007/s10458-011-9181-6 [114] LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444 doi: 10.1038/nature14539 [115] Nedić A, Liu J. Distributed optimization for control. Annual Review of Control, Robotics, and Autonomous Systems, 2018, 1: 77-103 doi: 10.1146/annurev-control-060117-105131 [116] 王龙, 田野, 杜金铭. 社会网络上的观念动力学. 中国科学: 信息科学, 2018, 48(1): 3-23 doi: 10.1360/N112017-00096Wang Long, Tian Ye, Du Jin-Ming. Opinion dynamics in social networks. Scientia Sinica Informationis, 2018, 48(1): 3-23 doi: 10.1360/N112017-00096 [117] Wu B, Du J M, Wang L. Bridging the gap between opinion dynamics and evolutionary game theory: Some equivalence results. In: Proceedings of the 39th Chinese Control Conference. Shenyang, China: IEEE, 2020. 6707−6714 [118] Levins R. Evolution in Changing Environments: Some Theoretical Explorations. Princeton, USA: Princeton University Press, 1968. [119] Hennes D, Morrill D, Omidshafiei S, Munos R, Perolat J, Lanctot M, et al. Neural replicator dynamics: Multiagent learning via hedging policy gradients. In: Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems. Auckland, New Zealand: International Foundation for Autonomous Agents and Multiagent Systems, 2020. 492−501 [120] Pantoja A, Quijano N, Passino K M. Dispatch of distributed generators using a local replicator equation. In: Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, USA: IEEE, 2011. 7494−7499 [121] Barreiro-Gomez J, Obando G, Quijano N. Distributed population dynamics: Optimization and control applications. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(2): 304-314 [122] Mei W J, Friedkin N E, Lewis K, Bullo F. Dynamic models of appraisal networks explaining collective learning. IEEE Transactions on Automatic Control, 2018, 63(9): 2898-2912 doi: 10.1109/TAC.2017.2775963 [123] Weitz J S, Eksin C, Paarporn K, Brown S P, Ratcliff W C. An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(47): E7518-E7525 [124] Chen X J, Szolnoki A. Punishment and inspection for governing the commons in a feedback-evolving game. PLoS Computational Biology, 2018, 14(7): Article No. e1006347 doi: 10.1371/journal.pcbi.1006347 [125] Wang X, Zheng Z M, Fu F. Steering eco-evolutionary game dynamics with manifold control. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2020, 476(2233): Article No. 20190643 doi: 10.1098/rspa.2019.0643 [126] Tilman A R, Plotkin J B, Akçay E. Evolutionary games with environmental feedbacks. Nature Communications, 2020, 11(1): Article No. 915 doi: 10.1038/s41467-020-14531-6 [127] Traulsen A, Hauert C. Stochastic evolutionary game dynamics. In: Heinz Georg Schuster, editor, Reviews of Nonlinear Dynamics and Complexity. Weinheim: Wiley-VCH, 2009. 25−61 [128] Moran P A P. The Statistical Processes of Evolutionary Theory. Oxford: Clarendon Press, 1962. [129] Nowak M A, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature, 2004, 428(6983): 646-650 doi: 10.1038/nature02414 [130] Taylor C, Fudenberg D, Sasaki A, Nowak M A. Evolutionary game dynamics in finite populations. Bulletin of Mathematical Biology, 2004, 66(6): 1621-1644 doi: 10.1016/j.bulm.2004.03.004 [131] Traulsen A, Shoresh N, Nowak M A. Analytical results for individual and group selection of any intensity. Bulletin of Mathematical Biology, 2008, 70(5): 1410-1424 doi: 10.1007/s11538-008-9305-6 [132] Claussen J C, Traulsen A. Cyclic dominance and biodiversity in well-mixed populations. Physical Review Letters, 2008, 100(5): Article No. 058104 [133] Wild G, Traulsen A. The different limits of weak selection and the evolutionary dynamics of finite populations. Journal of Theoretical Biology, 2007, 247(2): 382-390 doi: 10.1016/j.jtbi.2007.03.015 [134] Wu B, Altrock P M, Wang L, Traulsen A. Universality of weak selection. Physical Review E, 2010, 82(4): Article No. 046106 [135] Fudenberg D, Nowak M A, Taylor C, Imhof L A. Evolutionary game dynamics in finite populations with strong selection and weak mutation. Theoretical Population Biology, 2006, 70(3): 352-363 doi: 10.1016/j.tpb.2006.07.006 [136] Antal T, Nowak M A, Traulsen A. Strategy abundance in 2×2 games for arbitrary mutation rates. Journal of Theoretical Biology, 2009, 257(2): 340-344 doi: 10.1016/j.jtbi.2008.11.023 [137] Wu B, Traulsen A, Gokhale C S. Dynamic properties of evolutionary multi-player games in finite populations. Games, 2013, 4(2): 182-199 doi: 10.3390/g4020182 [138] Traulsen A, Pacheco J M, Nowak M A. Pairwise comparison and selection temperature in evolutionary game dynamics. Journal of Theoretical Biology, 2007, 246(3): 522-529 doi: 10.1016/j.jtbi.2007.01.002 [139] Traulsen A, Claussen J C, Hauert C. Coevolutionary dynamics: From finite to infinite populations. Physical Review Letters, 2005, 95(23): Article No. 238701 doi: 10.1103/PhysRevLett.95.238701 [140] Traulsen A, Claussen J C, Hauert C. Coevolutionary dynamics in large, but finite populations. Physical Review E, 2006, 74(1): Article No. 011901 [141] Huang F, Chen X J, Wang L. Role of the effective payoff function in evolutionary game dynamics. EPL (Europhysics Letters), 2018, 124(4): Article No. 40002 doi: 10.1209/0295-5075/124/40002 [142] Huang F, Chen X J, Wang L. Evolutionary dynamics of networked multi-person games: Mixing opponent-aware and opponent-independent strategy decisions. New Journal of Physics, 2019, 21(6): Article No. 063013 [143] 王龙, 伏锋, 陈小杰, 王靖, 李卓政, 谢广明, 等. 复杂网络上的演化博弈. 智能系统学报, 2007, 2(2): 1-10Wang Long, Fu Feng, Chen Xiao-Jie, Wang Jing, Li Zhuo-Zheng, Xie Guang-Ming, et al. Evolutionary games on complex networks. CAAI Transactions on Intelligent Systems, 2007, 2(2): 1-10 [144] 王龙, 武斌, 杜金铭, 魏钰婷, 周达. 复杂动态网络上的传播行为分析. 中国科学: 信息科学, 2020, 50(11): 1714-1731 doi: 10.1360/SSI-2020-0087Wang Long, Wu Bin, Du Jin-Ming, Wei Yu-Ting, Zhou Da. Spreading dynamics on complex dynamical networks. Scientia Sinica Informationis, 2020, 50(11): 1714-1731 doi: 10.1360/SSI-2020-0087 [145] Lieberman E, Hauert C, Nowak M A. Evolutionary dynamics on graphs. Nature, 2005, 433(7023): 312-316 doi: 10.1038/nature03204 [146] Ohtsuki H, Hauert C, Lieberman E, Nowak M A. A simple rule for the evolution of cooperation on graphs and social networks. Nature, 2006, 441(7092): 502-505 doi: 10.1038/nature04605 [147] Taylor P D, Day T, Wild G. Evolution of cooperation in a finite homogeneous graph. Nature, 2007, 447(7143): 469-472 doi: 10.1038/nature05784 [148] Su Q, Li A M, Wang L. Evolutionary dynamics under interactive diversity. New Journal of Physics, 2017, 19(10): Article No. 103023 doi: 10.1088/1367-2630/aa8feb [149] Su Q, Zhou L, Wang L. Evolutionary multiplayer games on graphs with edge diversity. PLoS Computational Biology, 2019, 15(4): Article No. e1006947 doi: 10.1371/journal.pcbi.1006947 [150] Su Q, McAvoy A, Wang L, Nowak M A. Evolutionary dynamics with game transitions. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(51): 25398-25404 doi: 10.1073/pnas.1908936116 [151] Li A, Cornelius S P, Liu Y Y, Wang L, Barabási A L. The fundamental advantages of temporal networks. Science, 2017, 358(6366): 1042-1046 doi: 10.1126/science.aai7488 [152] Li A M, Zhou L, Su Q, Cornelius S P, Liu Y Y, Wang L, Levin S A. Evolution of cooperation on temporal networks. Nature Communications, 2020, 11(1): Article No. 2259 doi: 10.1038/s41467-020-16088-w [153] 王龙, 吴特, 张艳玲. 共演化博弈中的反馈机制. 控制理论与应用, 2014, 31(7): 823-836 doi: 10.7641/CTA.2014.40059Wang Long, Wu Te, Zhang Yan-Ling. Feedback mechanism in coevolutionary games. Control Theory & Applications, 2014, 31(7): 823-836 doi: 10.7641/CTA.2014.40059 [154] 王龙, 杜金铭. 多智能体协调控制的演化博弈方法. 系统科学与数学, 2016, 36(3): 302-318 doi: 10.12341/jssms12735Wang Long, Du Jin-Ming. Evolutionary game theoretic approach to coordinated control of multi-agent systems. Journal of Systems Science and Mathematical Sciences, 2016, 36(3): 302-318 doi: 10.12341/jssms12735 [155] Wu T, Fu F, Wang L. Evolutionary games and spatial periodicity. arXiv: 2209.08267, 2022. [156] Axelrod R, Hamilton W D. The evolution of cooperation. Science, 1981, 211(4489): 1390-1396 doi: 10.1126/science.7466396 [157] Nowak M, Sigmund K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner’s dilemma game. Nature, 1993, 364(6432): 56-58 doi: 10.1038/364056a0 [158] Blume L E. The statistical mechanics of strategic interaction. Games and Economic Behavior, 1993, 5(3): 387-424 doi: 10.1006/game.1993.1023 [159] Lessard S. Long-term stability from fixation probabilities in finite populations: New perspectives for ESS theory. Theoretical Population Biology, 2005, 68(1): 19-27 doi: 10.1016/j.tpb.2005.04.001 [160] Imhof L A, Nowak M A. Evolutionary game dynamics in a Wright-Fisher process. Journal of Mathematical Biology, 2006, 52(5): 667-681 doi: 10.1007/s00285-005-0369-8 [161] Du J M, Wu B, Altrock P M, Wang L. Aspiration dynamics of multi-player games in finite populations. Journal of the Royal Society Interface, 2014, 11(94): Article No. 20140077 doi: 10.1098/rsif.2014.0077 [162] Du J M, Wu B, Wang L. Aspiration dynamics in structured population acts as if in a well-mixed one. Scientific Reports, 2015, 5: Article No. 8014 doi: 10.1038/srep08014 [163] Wu B, Zhou L. Individualised aspiration dynamics: Calculation by proofs. PLoS Computational Biology, 2018, 14(9): Article No. e1006035 doi: 10.1371/journal.pcbi.1006035 [164] Zhou L, Wu B, Vasconcelos V V, Wang L. Simple property of heterogeneous aspiration dynamics: Beyond weak selection. Physical Review E, 2018, 98(6): Article No. 062124 [165] Zhou L, Wu B, Du J M, Wang L. Aspiration dynamics generate robust predictions in heterogeneous populations. Nature Communications, 2021, 12(1): Article No. 3250 doi: 10.1038/s41467-021-23548-4 [166] Shapley L S. Stochastic games. Proceedings of the National Academy of Sciences of the United States of America, 1953, 39(10): 1095-1100 doi: 10.1073/pnas.39.10.1095 [167] Solan E, Vieille N. Stochastic games. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(45): 13743-13746 doi: 10.1073/pnas.1513508112 [168] Bellman R. A markovian decision process. Journal of Mathematics and Mechanics, 1957, 6(5): 679-684 [169] Puterman M L. Markov Decision Processes: Discrete Stochastic Dynamic Programming. New York: John Wiley & Sons, 2014. [170] Fink A M. Equilibrium in a stochastic n-person game. Journal of Science of the Hiroshima University, Series A-I Mathematics, 1964, 28(1): 89-93 [171] Maskin E, Tirole J. Markov perfect equilibrium: I. Observable actions. Journal of Economic Theory, 2001, 100(2): 191-219 doi: 10.1006/jeth.2000.2785 [172] Daskalakis C, Goldberg P W, Papadimitriou C H. The complexity of computing a Nash equilibrium. SIAM Journal on Computing, 2009, 39(1): 195-259 doi: 10.1137/070699652 [173] Harsanyi J C. Games with incomplete information played by “Bayesian” players, I-Ⅲ. Management Science, 1967, 14(3, 5, 7): 159–182, 320–334, 486–502 [174] Gibbons R. A Primer in Game Theory. Hoboken: Prentice Hall, 1992. [175] Dekel E, Fudenberg D. Rational behavior with payoff uncertainty. Journal of Economic Theory, 1990, 52(2): 243-267 doi: 10.1016/0022-0531(90)90033-G [176] Morris S. The common prior assumption in economic theory. Economics & Philosophy, 1995, 11(2): 227-253 [177] Mertens J F, Zamir S. Formulation of Bayesian analysis for games with incomplete information. International Journal of Game Theory, 1985, 14(1): 1-29 doi: 10.1007/BF01770224 [178] Holmström B, Myerson R B. Efficient and durable decision rules with incomplete information. Econometrica, 1983, 51(6): 1799-1819 doi: 10.2307/1912117 [179] Ben-Tal A, El Ghaoui L, Nemirovski A. Robust Optimization. Princeton, USA: Princeton University Press, 2009. [180] Aghassi M, Bertsimas D. Robust game theory. Mathematical Programming, 2006, 107(1): 231-273 [181] Kardeş E, Ordóñez F, Hall R W. Discounted robust stochastic games and an application to queueing control. Operations Research, 2011, 59(2): 365-382 doi: 10.1287/opre.1110.0931 [182] 黄锋. 博弈系统动力学与学习理论研究 [博士学位论文], 北京大学, 中国, 2022Huang Feng. System Dynamics and Learning Theory in Games [Ph.D. dissertation], Peking University, China, 2022 [183] Hardin G. The tragedy of the commons: The population problem has no technical solution; it requires a fundamental extension in morality. Science, 1968, 162(3859): 1243-1248 doi: 10.1126/science.162.3859.1243 [184] Robinson J. An iterative method of solving a game. Annals of Mathematics, 1951, 54(2): 296-301 doi: 10.2307/1969530 [185] Berger U. Brown’s original fictitious play. Journal of Economic Theory, 2007, 135(1): 572-578 doi: 10.1016/j.jet.2005.12.010 [186] Hernandez-Leal P, Kaisers M, Baarslag T, de Cote E M. A survey of learning in multiagent environments: Dealing with non-stationarity. arXiv: 1707.09183, 2017. [187] Albrecht S V, Stone P. Autonomous agents modelling other agents: A comprehensive survey and open problems. Artificial Intelligence, 2018, 258: 66-95 doi: 10.1016/j.artint.2018.01.002 [188] Li T, Zhao Y H, Zhu Q Y. The role of information structures in game-theoretic multi-agent learning. Annual Reviews in Control, 2022, 53: 296-314 doi: 10.1016/j.arcontrol.2022.03.003 [189] Marden J R, Arslan G, Shamma J S. Joint strategy fictitious play with inertia for potential games. IEEE Transactions on Automatic Control, 2009, 54(2): 208-220 doi: 10.1109/TAC.2008.2010885 [190] Swenson B, Kar S, Xavier J. Empirical centroid fictitious play: An approach for distributed learning in multi-agent games. IEEE Transactions on Signal Processing, 2015, 63(15): 3888-3901 doi: 10.1109/TSP.2015.2434327 [191] Eksin C, Ribeiro A. Distributed fictitious play for multiagent systems in uncertain environments. IEEE Transactions on Automatic Control, 2018, 63(4): 1177-1184 doi: 10.1109/TAC.2017.2747767 [192] Swenson B, Kar S, Xavier J. Single sample fictitious play. IEEE Transactions on Automatic Control, 2017, 62(11): 6026-6031 doi: 10.1109/TAC.2017.2709548 [193] Heinrich J, Silver D. Deep reinforcement learning from self-play in imperfect-information games. arXiv: 1603.01121, 2016. [194] Sayin M O, Parise F, Ozdaglar A. Fictitious play in zero-sum stochastic games. SIAM Journal on Control and Optimization, 2022, 60(4): 2095-2114 doi: 10.1137/21M1426675 [195] Perrin S, Perolat J, Laurière M, Geist M, Elie R, Pietquin O. Fictitious play for mean field games: Continuous time analysis and applications. In: Proceedings of the 34th Conference on Neural Information Processing Systems. Vancouver, Canada: MIT Press, 2020. 13199−13213 [196] Thorndike E L. Animal Intelligence: Experimental Studies. New York, USA: Macmillan, 1911. [197] Sutton R S, Barto A G. Reinforcement Learning: An Introduction. Cambridge, USA: MIT Press, 2018. [198] Sato Y, Akiyama E, Crutchfield J P. Stability and diversity in collective adaptation. Physica D: Nonlinear Phenomena, 2005, 210(1-2): 21-57 doi: 10.1016/j.physd.2005.06.031 [199] Galla T, Farmer J D. Complex dynamics in learning complicated games. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(4): 1232-1236 doi: 10.1073/pnas.1109672110 [200] Barfuss W, Donges J F, Kurths J. Deterministic limit of temporal difference reinforcement learning for stochastic games. Physical Review E, 2019, 99(4): Article No. 043305 [201] Kianercy A, Galstyan A. Dynamics of Boltzmann Q learning in two-player two-action games. Physical Review E, 2012, 85(4): Article No. 041145 [202] Galla T. Intrinsic noise in game dynamical learning. Physical Review Letters, 2009, 103(19): Article No. 198702 doi: 10.1103/PhysRevLett.103.198702 [203] Kaisers M, Tuyls K. Frequency adjusted multi-agent Q-learning. In: Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems. Toronto, Canada: International Foundation for Autonomous Agents and Multiagent Systems, 2010. 309−316 [204] Abdallah S, Lesser V. A multiagent reinforcement learning algorithm with non-linear dynamics. Journal of Artificial Intelligence Research, 2008, 33: 521-549 doi: 10.1613/jair.2628 [205] Klos T, van Ahee G J, Tuyls K. Evolutionary dynamics of regret minimization. In: Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Barcelona, Spain: Springer, 2010. 82−96 [206] Huang F, Cao M, Wang L. Learning enables adaptation in cooperation for multi-player stochastic games. Journal of the Royal Society Interface, 2020, 17(172): Article No. 20200639 doi: 10.1098/rsif.2020.0639 [207] Sutton R S, McAllester D, Singh S, Mansour Y. Policy gradient methods for reinforcement learning with function approximation. In: Proceedings of the 12th International Conference on Neural Information Processing Systems. Denver, USA: MIT Press, 1999. 1057−1063 [208] Konda V R, Tsitsiklis J N. Actor-critic algorithms. In: Proceedings of the 12th International Conference on Neural Information Processing Systems. Denver, USA: MIT Press, 1999. 1008−1014 [209] Arapostathis A, Borkar V S, Fernández-Gaucherand E, Ghosh M K, Marcus S I. Discrete-time controlled Markov processes with average cost criterion: A survey. SIAM Journal on Control and Optimization, 1993, 31(2): 282-344 doi: 10.1137/0331018 [210] Bellman R E. Dynamic Programming. Princeton, USA: Princeton University Press, 1957. [211] Bertsekas D P, Tsitsiklis J N. Neuro-Dynamic Programming. Belmont, USA: Athena Scientific, 1996. [212] Kaelbling L P, Littman M L, Moore A W. Reinforcement learning: A survey. Journal of Artificial Intelligence Research, 1996, 4: 237-285 doi: 10.1613/jair.301 [213] Hessel M, Modayil J, van Hasselt H, Schaul T, Ostrovski G, Dabney W, et al. Rainbow: Combining improvements in deep reinforcement learning. In: Proceedings of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. New Orleans, USA: AAAI Press, 2018. 3215−3222 [214] Kocsis L, Szepesvári C. Bandit based Monte-Carlo planning. In: Proceedings of the 17th European Conference on Machine Learning. Berlin, Germany: Springer, 2006. 282−293 [215] Coulom R. Efficient selectivity and backup operators in Monte-Carlo tree search. In: Proceedings of the 5th International Conference on Computers and Games. Turin, Italy: Springer, 2006. 72−83 [216] Silver D, Lever G, Heess N, Degris T, Wierstra D, Riedmiller M. Deterministic policy gradient algorithms. In: Proceedings of the 31st International Conference on Machine Learning. Beijing, China: JMLR.org, 2014. 387−395 [217] Lillicrap T P, Hunt J J, Pritzel A, Heess N, Erez T, Tassa Y, et al. Continuous control with deep reinforcement learning. In: Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico: OpenReview.net, 2016. 1−10 [218] Schulman J, Levine S, Moritz P, Jordan M, Abbeel P. Trust region policy optimization. In: Proceedings of the 32nd International Conference on Machine Learning. Lille, France: JMLR.org, 2015. 1889−1897 [219] Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. arXiv: 1707.06347, 2017. [220] Mnih V, Badia A P, Mirza M, Graves A, Harley T, Lillicrap T P, et al. Asynchronous methods for deep reinforcement learning. In: Proceedings of the 33rd International Conference on Machine Learning. New York, USA: JMLR.org, 2016. 1928−1937 [221] Haarnoja T, Zhou A, Abbeel P, Levine S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In: Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden: PMLR, 2018. 1861−1870 [222] Claus C, Boutilier C. The dynamics of reinforcement learning in cooperative multiagent systems. In: Proceedings of the 15th National Conference on Artificial Intelligence and 10th Innovative Applications of Artificial Intelligence. Madison, USA: AAAI Press, 1998. 746−752 [223] Littman M L. Value-function reinforcement learning in Markov games. Cognitive Systems Research, 2001, 2(1): 55-66 doi: 10.1016/S1389-0417(01)00015-8 [224] Foerster J N, Assael Y M, de Freitas N, Whiteson S. Learning to communicate with deep multi-agent reinforcement learning. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: MIT Press, 2016. 2145−2153 [225] García J, Fernández F. A comprehensive survey on safe reinforcement learning. Journal of Machine Learning Research, 2015, 16(1): 1437-1480 [226] Hernandez-Leal P, Kartal B, Taylor M E. A survey and critique of multiagent deep reinforcement learning. Autonomous Agents and Multi-Agent Systems, 2019, 33(6): 750-797 doi: 10.1007/s10458-019-09421-1 [227] Da Silva F L, Costa A H R. A survey on transfer learning for multiagent reinforcement learning systems. Journal of Artificial Intelligence Research, 2019, 64: 645-703 doi: 10.1613/jair.1.11396 [228] Oroojlooy A, Hajinezhad D. A review of cooperative multi-agent deep reinforcement learning. Applied Intelligence, 2022. [229] Nguyen T T, Nguyen N D, Nahavandi S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE Transactions on Cybernetics, 2020, 50(9): 3826-3839 doi: 10.1109/TCYB.2020.2977374 [230] Heuillet A, Couthouis F, Díaz-Rodríguez N. Explainability in deep reinforcement learning. Knowledge-Based Systems, 2021, 214: Article No. 106685 doi: 10.1016/j.knosys.2020.106685 [231] Dulac-Arnold G, Levine N, Mankowitz D J, Li J, Paduraru C, Gowal S, et al. Challenges of real-world reinforcement learning: Definitions, benchmarks and analysis. Machine Learning, 2021, 110(9): 2419-2468 doi: 10.1007/s10994-021-05961-4 [232] Parker-Holder J, Rajan R, Song X Y, Biedenkapp A, Miao Y J, Eimer T, et al. Automated reinforcement learning (AutoRL): A survey and open problems. Journal of Artificial Intelligence Research , 2022, 74: 517-568 doi: 10.1613/jair.1.13596 [233] Morimoto J, Doya K. Robust reinforcement learning. Neural Computation, 2005, 17(2): 335-359 doi: 10.1162/0899766053011528 [234] Moos J, Hansel K, Abdulsamad H, Stark S, Clever D, Peters J. Robust reinforcement learning: A review of foundations and recent advances. Machine Learning and Knowledge Extraction, 2022, 4(1): 276-315 doi: 10.3390/make4010013 [235] Satia J K, Lave R E Jr. Markovian decision processes with uncertain transition probabilities. Operations Research, 1973, 21(3): 728-740 doi: 10.1287/opre.21.3.728 [236] White Ⅲ C C, Eldeib H K. Markov decision processes with imprecise transition probabilities. Operations Research, 1994, 42(4): 739-749 doi: 10.1287/opre.42.4.739 [237] Zhou K, Doyle J C, Glover K. Robust and Optimal Control. Upper Saddle River, USA: Prentice Hall, 1996. [238] Nilim A, El Ghaoui L. Robust control of Markov decision processes with uncertain transition matrices. Operations Research, 2005, 53(5): 780-798 doi: 10.1287/opre.1050.0216 [239] Iyengar G N. Robust dynamic programming. Mathematics of Operations Research, 2005, 30(2): 257-280 doi: 10.1287/moor.1040.0129 [240] Goodfellow I J, Pouget-Abadie J, Mirza M, Xu M, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 2672−2680 [241] Kaufman D L, Schaefer A J. Robust modified policy iteration. INFORMS Journal on Computing, 2013, 25(3): 396-410 doi: 10.1287/ijoc.1120.0509 [242] Xu H, Mannor S. The robustness-performance tradeoff in Markov decision processes. In: Proceedings of the 19th International Conference on Neural Information Processing Systems. Vancouver, Canada: MIT Press, 2006. 1537−1544 [243] Delage E, Mannor S. Percentile optimization for Markov decision processes with parameter uncertainty. Operations Research, 2010, 58(1): 203-213 doi: 10.1287/opre.1080.0685 [244] Turchetta M, Krause A, Trimpe S. Robust model-free reinforcement learning with multi-objective Bayesian optimization. In: Proceedings of IEEE International Conference on Robotics and Automation (ICRA). Paris, France: IEEE, 2020. 10702−10708 [245] Mannor S, Mebel O, Xu H. Robust MDPs with k-rectangular uncertainty. Mathematics of Operations Research, 2016, 41(4): 1484-1509 doi: 10.1287/moor.2016.0786 [246] Goyal V, Grand-Clément J. Robust Markov decision processes: Beyond rectangularity. Mathematics of Operations Research, 2022. [247] Gilboa I, Schmeidler D. Maxmin expected utility with non-unique prior. Journal of Mathematical Economics, 1989, 18(2): 141-153 doi: 10.1016/0304-4068(89)90018-9 [248] Xu H, Mannor S. Distributionally robust Markov decision processes. Mathematics of Operations Research, 2012, 37(2): 288-300 doi: 10.1287/moor.1120.0540 [249] Tamar A, Mannor S, Xu H. Scaling up robust MDPs using function approximation. In: Proceedings of the 31st International Conference on Machine Learning. Beijing, China: JMLR.org, 2014. 181−189 [250] Scherrer B, Ghavamzadeh M, Gabillon V, Lesner B, Geist M. Approximate modified policy iteration and its application to the game of Tetris. The Journal of Machine Learning Research, 2015, 16(1): 1629-1676 [251] Badrinath K P, Kalathil D. Robust reinforcement learning using least squares policy iteration with provable performance guarantees. In: Proceedings of the 38th International Conference on Machine Learning. Virtual: PMLR, 2021. 511−520 [252] Pinto L, Davidson J, Sukthankar R, Gupta A. Robust adversarial reinforcement learning. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: JMLR.org, 2017. 2817−2826 [253] Phan T, Belzner L, Gabor T, Sedlmeier A, Ritz F, Linnhoff-Popien C. Resilient multi-agent reinforcement learning with adversarial value decomposition. In: Proceedings of the 35th AAAI Conference on Artificial Intelligence. Virtual: AAAI Press, 2021. 11308−11316 [254] Everett M, Lütjens B, How J P. Certifiable robustness to adversarial state uncertainty in deep reinforcement learning. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(9): 4184-4198 doi: 10.1109/TNNLS.2021.3056046 [255] Mankowitz D J, Levine N, Jeong R, Abdolmaleki A, Springenberg J T, Shi Y Y, et al. Robust reinforcement learning for continuous control with model misspecification. In: Proceedings of the 8th International Conference on Learning Representations. Addis Ababa, Ethiopia: OpenReview.net, 2020. 1−11 [256] Si N, Zhang F, Zhou Z Y, Blanchet J. Distributionally robust policy evaluation and learning in offline contextual bandits. In: Proceedings of the 37th International Conference on Machine Learning. Vienna, Austria: JMLR.org, 2020. 8884−8894 [257] Zhou Z Q, Bai Q X, Zhou Z Y, Qiu L H, Blanchet J H, Glynn P W. Finite-sample regret bound for distributionally robust offline tabular reinforcement learning. In: Proceedings of the 24th International Conference on Artificial Intelligence and Statistics. San Diego, USA: PMLR, 2021. 3331−3339 [258] Zhang K Q, Sun T, Tao Y Z, Genc S, Mallya S, Başar T. Robust multi-agent reinforcement learning with model uncertainty. In: Proceedings of the 34th Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc, 2020. 10571–10583 [259] Huang F, Cao M, Wang L. Robust optimal policies for team Markov games. arXiv: 2105.07405, 2021. [260] Lewis F L, Vrabie D L, Syrmos V L. Optimal Control. Hoboken, USA: John Wiley & Sons, 2012. [261] Bertsekas D P. Reinforcement Learning and Optimal Control. Belmont, USA: Athena Scientific, 2019. [262] Bryson A E. Optimal control-1950 to 1985. IEEE Control Systems Magazine, 1996, 16(3): 26-33 doi: 10.1109/37.506395 [263] Doya K. Reinforcement learning in continuous time and space. Neural Computation, 2000, 12(1): 219-245 doi: 10.1162/089976600300015961 [264] Liu D R, Wei Q L, Wang D, Yang X, Li H L. Adaptive Dynamic Programming with Applications in Optimal Control. Cham, Switzerland: Springer, 2017. [265] Jiang Z P, Jiang Y. Robust adaptive dynamic programming for linear and nonlinear systems: An overview. European Journal of Control, 2013, 19(5): 417-425 doi: 10.1016/j.ejcon.2013.05.017 [266] Fu K S. Learning control systems-review and outlook. IEEE Transactions on Automatic Control, 1970, 15(2): 210-221 doi: 10.1109/TAC.1970.1099405 [267] Vrabie D, Lewis F. Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Networks, 2009, 22(3): 237-246 doi: 10.1016/j.neunet.2009.03.008 [268] Modares H, Lewis F L, Naghibi-Sistani M B. Integral reinforcement learning and experience replay for adaptive optimal control of partially-unknown constrained-input continuous-time systems. Automatica, 2014, 50(1): 193-202 doi: 10.1016/j.automatica.2013.09.043 [269] Jiang Y, Jiang Z P. Robust adaptive dynamic programming and feedback stabilization of nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(5): 882-893 doi: 10.1109/TNNLS.2013.2294968 [270] Isaacs R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization. Mineola, USA: Dover Publications, 1999. [271] Ho Y, Bryson A, Baron S. Differential games and optimal pursuit-evasion strategies. IEEE Transactions on Automatic Control, 1965, 10(4): 385-389 doi: 10.1109/TAC.1965.1098197 [272] Starr A W, Ho Y C. Nonzero-sum differential games. Journal of Optimization Theory and Applications, 1969, 3(3): 184-206 doi: 10.1007/BF00929443 [273] Vamvoudakis K G, Lewis F L. Multi-player non-zero-sum games: Online adaptive learning solution of coupled Hamilton-Jacobi equations. Automatica, 2011, 47(8): 1556-1569 doi: 10.1016/j.automatica.2011.03.005 [274] Vamvoudakis K G, Lewis F L, Hudas G R. Multi-agent differential graphical games: Online adaptive learning solution for synchronization with optimality. Automatica, 2012, 48(8): 1598-1611 doi: 10.1016/j.automatica.2012.05.074 [275] Kamalapurkar R, Klotz J R, Walters P, Dixon W E. Model-based reinforcement learning in differential graphical games. IEEE Transactions on Control of Network Systems, 2018, 5(1): 423-433 doi: 10.1109/TCNS.2016.2617622 [276] Li M, Qin J H, Freris N M, Ho D W C. Multiplayer Stackelberg-Nash game for nonlinear system via value iteration-based integral reinforcement learning. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(4): 1429-1440 doi: 10.1109/TNNLS.2020.3042331 [277] 郭雷. 关于控制理论发展的某些思考. 系统科学与数学, 2011, 31(9): 1014−1018Guo Lei. Some thoughts on the development of control theory. Journal of Systems Science and Mathematical Sciences, 2011, 31(9): 1014−1018 [278] Zhang R R, Guo L. Controllability of Nash equilibrium in game-based control systems. IEEE Transactions on Automatic Control, 2019, 64(10): 4180-4187 doi: 10.1109/TAC.2019.2893150 [279] Zhang R R, Guo L. Controllability of stochastic game-based control systems. SIAM Journal on Control and Optimization, 2019, 57(6): 3799-3826 doi: 10.1137/18M120854X [280] Zhang R R, Guo L. Stabilizability of game-based control systems. SIAM Journal on Control and Optimization, 2021, 59(5): 3999-4023 doi: 10.1137/20M133587X [281] Simaan M, Cruz Jr J B. On the Stackelberg strategy in nonzero-sum games. Journal of Optimization Theory and Applications, 1973, 11(5): 533-555 doi: 10.1007/BF00935665 [282] Li Y, Guo L. Towards a theory of stochastic adaptive differential games. In: Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, USA: IEEE, 2011. 5041−5046 [283] 袁硕, 郭雷. 随机自适应动态博弈. 中国科学: 数学, 2016, 46(10): 1367-1382Yuan Shuo, Guo Lei. Stochastic adaptive dynamical games. Scientia Sinica Mathematica, 2016, 46(10): 1367-1382 [284] Liu N, Guo L. Stochastic adaptive linear quadratic differential games. arXiv: 2204.08869, 2022. [285] Cheng D Z, Qi H S, Zhao Y. An Introduction to Semi-Tensor Product of Matrices and Its Applications. Singapore: World Scientific, 2012. [286] Cheng D Z, Qi H S, Li Z Q. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach. London: Springer, 2011. [287] Cheng D Z. On finite potential games. Automatica, 2014, 50(7): 1793-1801 doi: 10.1016/j.automatica.2014.05.005 [288] Cheng D Z, Wu Y H, Zhao G D, Fu S H. A comprehensive survey on STP approach to finite games. Journal of Systems Science and Complexity, 2021, 34(5): 1666-1680 doi: 10.1007/s11424-021-1232-8 [289] Cheng D Z, He F H, Qi H S, Xu T T. Modeling, analysis and control of networked evolutionary games. IEEE Transactions on Automatic Control, 2015, 60(9): 2402-2415 doi: 10.1109/TAC.2015.2404471 [290] Monderer D, Shapley L S. Potential games. Games and Economic Behavior, 1996, 14(1): 124-143 doi: 10.1006/game.1996.0044 [291] Cheng D Z, Liu T. From Boolean game to potential game. Automatica, 2018, 96: 51-60 doi: 10.1016/j.automatica.2018.06.028 [292] Li C X, Xing Y, He F H, Cheng D Z. A strategic learning algorithm for state-based games. Automatica, 2020, 113: Article No. 108615 doi: 10.1016/j.automatica.2019.108615 [293] Yang T, Yi X L, Wu J F, Yuan Y, Wu D, Meng Z Y, et al. A survey of distributed optimization. Annual Reviews in Control, 2019, 47: 278-305 doi: 10.1016/j.arcontrol.2019.05.006 [294] 王龙, 卢开红, 关永强. 分布式优化的多智能体方法. 控制理论与应用, 2019, 36(11): 1820-1833 doi: 10.7641/CTA.2019.90502Wang Long, Lu Kai-Hong, Guan Yong-Qiang. Distributed optimization via multi-agent systems. Control Theory & Applications, 2019, 36(11): 1820-1833 doi: 10.7641/CTA.2019.90502 [295] Facchinei F, Kanzow C. Generalized Nash equilibrium problems. Annals of Operations Research, 2010, 175(1): 177-211 doi: 10.1007/s10479-009-0653-x [296] Scutari G, Palomar D P, Facchinei F, Pang J S. Convex optimization, game theory, and variational inequality theory. IEEE Signal Processing Magazine, 2010, 27(3): 35-49 doi: 10.1109/MSP.2010.936021 [297] Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementarity Problems. New York, USA: Springer, 2003. [298] Nagurney A, Zhang D. Projected Dynamical Systems and Variational Inequalities with Applications. New York, USA: Springer, 1996. [299] Salehisadaghiani F, Pavel L. Distributed Nash equilibrium seeking: A gossip-based algorithm. Automatica, 2016, 72: 209-216 doi: 10.1016/j.automatica.2016.06.004 [300] Gadjov D, Pavel L. A passivity-based approach to Nash equilibrium seeking over networks. IEEE Transactions on Automatic Control, 2019, 64(3): 1077-1092 doi: 10.1109/TAC.2018.2833140 [301] Ye M J, Hu G Q. Distributed Nash equilibrium seeking by a consensus based approach. IEEE Transactions on Automatic Control, 2017, 62(9): 4811-4818 doi: 10.1109/TAC.2017.2688452 [302] Liang S, Yi P, Hong Y G. Distributed Nash equilibrium seeking for aggregative games with coupled constraints. Automatica, 2017, 85: 179-185 doi: 10.1016/j.automatica.2017.07.064 [303] Lu K H, Jing G S, Wang L. Distributed algorithms for searching generalized Nash equilibrium of noncooperative games. IEEE Transactions on Cybernetics, 2019, 49(6): 2362-2371 doi: 10.1109/TCYB.2018.2828118 [304] Lu K H, Li G Q, Wang L. Online distributed algorithms for seeking generalized Nash equilibria in dynamic environments. IEEE Transactions on Automatic Control, 2021, 66(5): 2289-2296 doi: 10.1109/TAC.2020.3002592 [305] Press W H, Dyson F J. Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(26): 10409-10413 doi: 10.1073/pnas.1206569109 [306] Stewart A J, Plotkin J B. Extortion and cooperation in the prisoner’s dilemma. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(26): 10134-10135 doi: 10.1073/pnas.1208087109 [307] Stewart A J, Plotkin J B. From extortion to generosity, evolution in the iterated prisoner's dilemma. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(38): 15348-15353 doi: 10.1073/pnas.1306246110 [308] Akin E. The iterated prisoner's dilemma: Good strategies and their dynamics. In: Assani Idris, editor, Ergodic Theory: Advances in Dynamical Systems. Berlin: De Gruyter, 2016. 77−107 [309] Hilbe C, Traulsen A, Sigmund K. Partners or rivals? Strategies for the iterated prisoner’s dilemma. Games and Economic Behavior, 2015, 92: 41-52 doi: 10.1016/j.geb.2015.05.005 [310] McAvoy A, Hauert C. Autocratic strategies for iterated games with arbitrary action spaces. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(13): 3573-3578 doi: 10.1073/pnas.1520163113 [311] Hilbe C, Wu B, Traulsen A, Nowak M A. Cooperation and control in multiplayer social dilemmas. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111(46): 16425-16430 doi: 10.1073/pnas.1407887111 [312] Pan L M, Hao D, Rong Z H, Zhou T. Zero-determinant strategies in iterated public goods game. Scientific Reports, 2015, 5: Article No. 13096 doi: 10.1038/srep13096 [313] Govaert A, Cao M. Zero-determinant strategies in repeated multiplayer social dilemmas with discounted payoffs. IEEE Transactions on Automatic Control, 2021, 66(10): 4575-4588 doi: 10.1109/TAC.2020.3032086 [314] Tan R F, Su Q, Wu B, Wang L. Payoff control in repeated games. In: Proceedings of the 33rd Chinese Control and Decision Conference. Kunming, China: Editorial Department of Control and Decision, 2021. 997−1005 [315] Chen J, Zinger A. The robustness of zero-determinant strategies in iterated prisoner’s dilemma games. Journal of Theoretical Biology, 2014, 357: 46-54 doi: 10.1016/j.jtbi.2014.05.004 [316] Adami C, Hintze A. Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nature Communications, 2013, 4(1): Article No. 2193 doi: 10.1038/ncomms3193 [317] Hilbe C, Nowak M A, Sigmund K. Evolution of extortion in iterated prisoner’ dilemma games. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(17): 6913-6918 doi: 10.1073/pnas.1214834110 [318] Chen F, Wu T, Wang L. Evolutionary dynamics of zero-determinant strategies in repeated multiplayer games. Journal of Theoretical Biology, 2022, 549: Article No. 111209 doi: 10.1016/j.jtbi.2022.111209 [319] Cheng Z Y, Chen G P, Hong Y G. Misperception influence on zero-determinant strategies in iterated prisoner’s dilemma. Scientific Reports, 2022, 12(1): Article No. 5174 doi: 10.1038/s41598-022-08750-8 [320] Barto A G. Reinforcement learning: Connections, surprises, and challenge. AI Magazine, 2019, 40(1): 3-15 doi: 10.1609/aimag.v40i1.2844 [321] Huang X W, Kroening D, Ruan W J, Sharp J, Sun Y C, Thamo E, et al. A survey of safety and trustworthiness of deep neural networks: Verification, testing, adversarial attack and defence, and interpretability. Computer Science Review, 2020, 37: Article No. 100270 doi: 10.1016/j.cosrev.2020.100270 [322] Kuhn H W. Extensive games and the problem of information. In: Kuhn H W and Tucker A W, editors, Contributions to the Theory of Games (AM-28), Volume Ⅱ. Princeton, USA: Princeton University Press, 1953. 193−216 [323] Bai Y, Jin C, Mei S, Yu T C. Near-optimal learning of extensive-form games with imperfect information. In: Proceedings of the 39th International Conference on Machine Learning. Baltimore, USA: PMLR, 2022. 1337−1382 [324] Spence M. Job market signaling. The Quarterly Journal of Economics, 1973, 87(3): 355-374 doi: 10.2307/1882010 [325] Meyer D A. Quantum strategies. Physical Review Letters, 1999, 82(5): 1052-1055 doi: 10.1103/PhysRevLett.82.1052 [326] Eisert J, Wilkens M, Lewenstein M. Quantum games and quantum strategies. Physical Review Letters, 1999, 83(15): 3077-3080 doi: 10.1103/PhysRevLett.83.3077 [327] Khan F S, Solmeyer N, Balu R, Humble T S. Quantum games: A review of the history, current state, and interpretation. Quantum Information Processing, 2018, 17(11): Article No. 309 doi: 10.1007/s11128-018-2082-8 [328] Huang M Y, Malhamé R P, Caines P E. Large population stochastic dynamic games: Closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Communications in Information and Systems, 2006, 6(3): 221-252 doi: 10.4310/CIS.2006.v6.n3.a5 [329] Lasry J M, Lions P L. Mean field games. Japanese Journal of Mathematics, 2007, 2(1): 229-260 doi: 10.1007/s11537-007-0657-8 [330] Weinan E. A proposal on machine learning via dynamical systems. Communications in Mathematics and Statistics, 2017, 5(1): 1-11 doi: 10.1007/s40304-017-0103-z [331] Chen R T Q, Rubanova Y, Bettencourt J, Duvenaud D. Neural ordinary differential equations. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc, 2018. 6572−6583 [332] Kidger P. On Neural Differential Equations [Ph.D. dissertation], University of Oxford, UK, 2022 -
















 下载:
下载: