A Multi-objective Internal Preload Optimization Method of Redundantly Actuated Parallel Robots Based on Variable Impedance Control
-
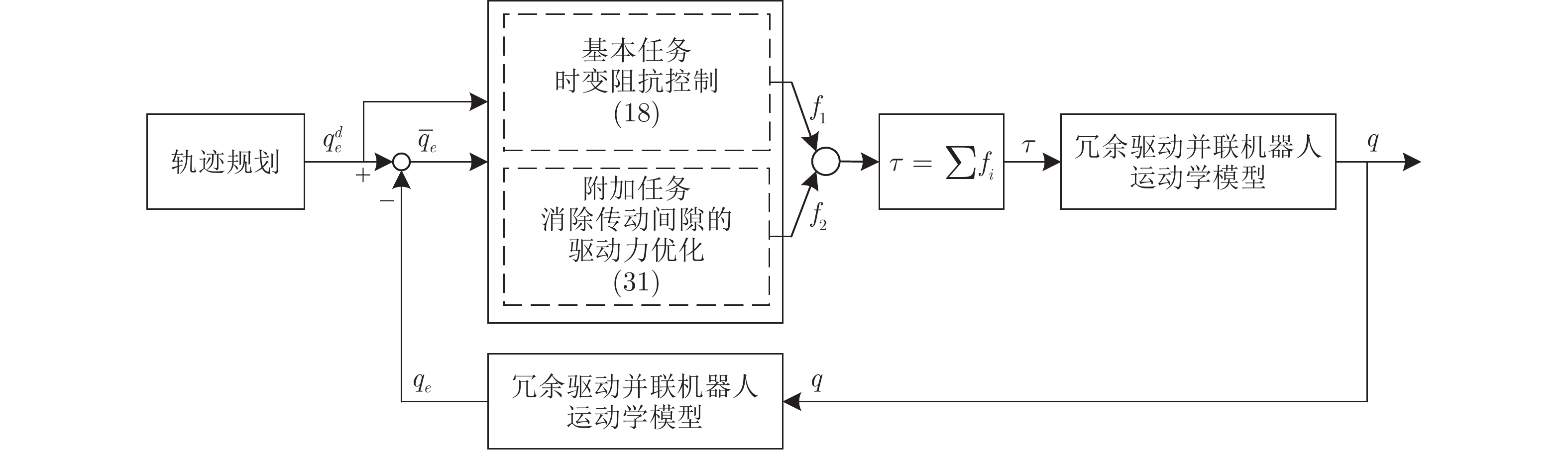
摘要: 由于冗余驱动的存在, 冗余驱动并联机器人系统逆动力学模型存在无限组可跟踪期望轨迹的控制力矩解, 这使得机器人在运行过程中具有完成附加任务的能力. 以实现骨科机器人的安全精准操控为目的, 提出了基于变阻抗控制的冗余驱动并联机器人多目标内力优化方法. 首先, 采用支链分解法对冗余驱动并联机器人的动力学进行建模. 其次, 为实现机器人的安全操作, 设计了冗余驱动并联机器人时变阻抗控制器, 利用李雅普诺夫理论分析了系统的稳定性; 在此基础上, 以消除冗余驱动并联机器人运动过程中的传动间隙为附加任务, 提出了一种以力矩传递性能、驱动功率和控制力为优化目标的多目标融合驱动力优化方法. 最后, 通过仿真实验与对比分析, 验证了所提方法的有效性, 实现了机器人系统传动间隙的消除.Abstract: Due to the existence of redundant actuation, the inverse dynamics model of the robot system has an infinite set of control torque solutions that can track the desired trajectory, which makes the redundantly actuated parallel manipulators capable of completing additional tasks during operation. In order to realize safe and precise operation of orthopedic robot, a multi-objective internal preload optimization method of redundantly actuated parallel robots based on variable impedance control is proposed in this paper. First, the dynamics of redundantly actuated parallel manipulator is modeled by using the branch chain decomposition method. Second, in order to realize safe operation, a time-varying impedance controller for redundantly actuated parallel robot is designed, and the stability of the robot system is analyzed by using the Lyapunov theory. On this basis, a multi-objective fusion internal preload optimization method is proposed, which takes torque transmission performance, driving power and control force as optimization objectives, to eliminate the backlash during the movement of redundantly actuated parallel robot. Finally, the effectiveness of the proposed method is verified through simulation experiments and comparative analysis, and the backlash of the robot system is eliminated.
-
图 1 平面二自由度冗余驱动并联机器人结构简图
Fig. 1 Schematic of the planar 2-DOF redundantly actuated parallel robot
图 6
$s = (1,1,1)$ 时预载力矩优化参数曲线Fig. 6 Internal preload optimization parameter curve when
$s = (1,1,1)$ 
图 7
$s = (1,1,1)$ 时机器人主动关节力矩曲线Fig. 7 Torque curve of the robot in joint space when
$s = (1,1,1)$ 
图 8
$s = (-1,-1,-1)$ 时预载力矩优化参数曲线Fig. 8 Internal preload optimization parameter curve when
$s = (-1,-1,-1)$ 
图 9
$s = (-1,-1,-1)$ 时机器人主动关节力矩曲线Fig. 9 Torque curve of the robot in joint space when
$s = (-1,-1,-1)$ 
图 10 本文所提方法与固定阻抗控制方法的机器人末端位置误差曲线
Fig. 10 Position error curve of the robot of the proposed method and the fixed impedance control method
图 11 本文所提方法与固定阻抗控制方法的机器人末端交互力曲线
Fig. 11 Interaction force curve of the robot of the proposed method and the fixed impedance control method
图 12 时变阻抗控制方法的机器人主动关节力矩曲线
Fig. 12 Torque curve of the robot in joint space based on time-varying impedance control method
图 13 未考虑消除传动间隙的机器人主动关节力矩曲线
Fig. 13 Torque curve of the robot in joint space without consideration of elimination of backlash
图 14
$s = (1,1,1)$ 时多目标加权归一化内力优化方法下预载力矩优化参数曲线Fig. 14 Internal preload optimization parameter curve under the multi-objective weighted normalized optimization method when
$s = (1,1,1)$ 
图 15
$s = (1,1,1)$ 时多目标加权归一化内力优化方法下机器人主动关节力矩曲线Fig. 15 Torque curve of the robot in joint space under the multi-objective weighted normalized optimization method when
$s = (1,1,1)$ 
图 16
$s = (-1,-1,-1)$ 时多目标加权归一化内力优化方法下预载力矩优化参数曲线Fig. 16 Internal preload optimization parameter curve under the multi-objective weighted normalized optimization method when
$s = (-1,-1,-1)$ 
图 17
$s = (-1,-1,-1)$ 时多目标加权归一化内力优化方法下机器人主动关节力矩曲线Fig. 17 Torque curve of the robot in joint space under the multi-objective weighted normalized optimization method when
$s = (-1,-1,-1)$ 
图 19
$s = (-1,-1,-1)$ 时多目标加权归一化内力优化方法下机器人笛卡尔空间位置曲线Fig. 19 Position curve of the robot in Cartesian space under the multi-objective weighted normalized optimization method when
$s = (-1,-1,-1)$ 
图 20
$s = (-1,-1,-1)$ 时多目标加权归一化内力优化方法下机器人关节空间位置曲线Fig. 20 Position curve of the robot in joint space under the multi-objective weighted normalized optimization method when
$s = (-1,-1,-1)$ 
图 21
$s = (-1,-1,-1)$ 时本文所提方法与串联机器人时变阻抗控制方法的机器人末端位置曲线Fig. 21 Position curve of the robot of the method proposed in this paper and the time-varying impedance control method of the serial robot when s = (−1, −1, −1)
表 1 冗余驱动并联机器人物理参数
Table 1 Physical parameters of redundantly actuated parallel robots
$m_{i1}$ $m_{i2}$ $l_{i1}$ $l_{i2}$ $r_{i1}$ $r_{i2}$ ${I_{i1}} = {m_{i1}}r_{i1}^2$ ${I_{i2}} = {m_{i2}}r_{i2}^2$ 2.0 kg 2.0 kg 0.50 m 0.60 m 0.25 m 0.30 m $0.125\;{\rm{kg} } \cdot {\rm{m} }^2$ $0.180\;{\rm{kg} } \cdot {\rm{m} }^2$ 
下载: 导出CSV
表 2 本文所提方法误差对比分析
Table 2 Comparison and analysis of the error of the proposed method
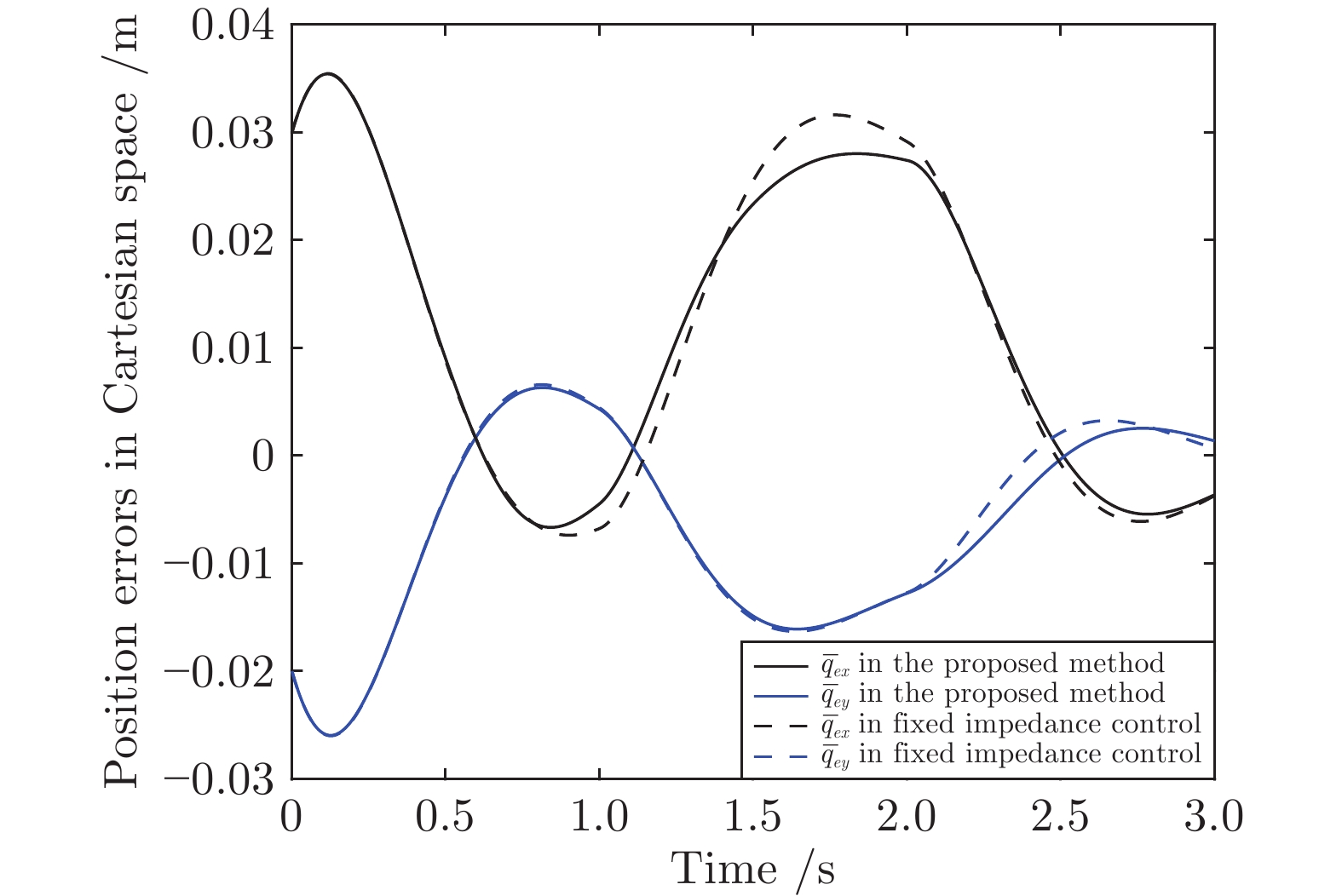
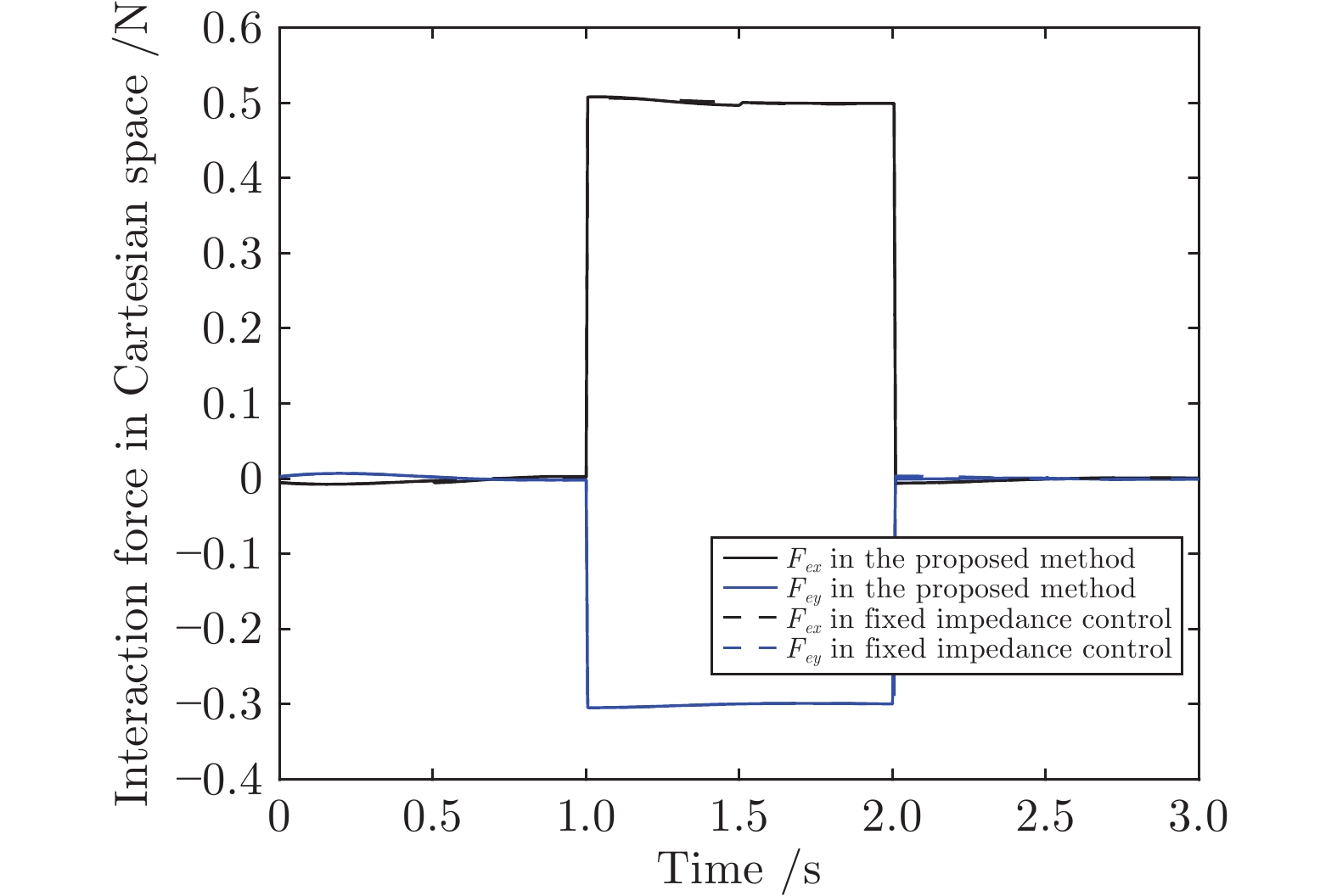
轨迹(m) ${\bar q_e}\;(\text{m})$ ${\dot {\bar q}_e}\;({\text{m/s}})$ ${F_e}\;({\text{N}})$ ${\bar d_x}\;(\text{m})$ ${\bar d_y}\; (\text{m})$ $\text{RMSE}\; (\text{m})$ $\text{JRMSE}\; (\text{rad})$ 式(34) ${[ {0.03} \;\;{ - 0.02} ]^{\rm{T}}}$ ${[{0.10}\;\;{ - 0.10}]^{\rm{T}}}$ 式(33) 0.0148 0.0090 0.0217 0.1141 式(37) ${[ {0.03}\;\;{ - 0.02} ]^{\rm{T}}}$ ${[ {0.10}\;\;{ - 0.10} ]^{\rm{T}}}$ 式(33) 0.0148 0.0090 0.0217 0.1113 式(34) ${[ {-0.02}\;\;{0.01} ]^{\rm{T}}}$ ${[{ - 0.05}\;\;{0.05}]^{\rm{T}}}$ 式(33) 0.0123 0.0069 0.0176 0.0954 式(37) ${[ {-0.02}\;\;{0.01} ]^{\rm{T}}}$ ${[ { - 0.05}\;\;{0.05} ]^{\rm{T}}}$ 式(33) 0.0123 0.0069 0.0176 0.0835 式(34) ${[ {0.05}\;\;{-0.03} ]^{\rm{T}}}$ ${[ { 0.20}\;\;{-0.15} ]^{\rm{T}}}$ 式(33) 0.0193 0.0110 0.0294 0.1508 式(37) ${[ {0.05}\;\;{-0.03} ]^{\rm{T}}}$ ${[ { 0.20}\;\;{-0.15} ]^{\rm{T}}}$ 式(33) 0.0193 0.0110 0.0294 0.1708 式(34) ${[ {0.03}\;\;{ - 0.02} ]^{\rm{T}}}$ ${[ {0.10}\;\;{ - 0.10} ]^{\rm{T}}}$ 式(38) 0.0107 0.0055 0.0166 0.0809 式(37) ${[ {0.03}\;\;{ - 0.02} ]^{\rm{T}}}$ ${[ {0.10}\;\;{ - 0.10} ]^{\rm{T}}}$ 式(38) 0.0107 0.0055 0.0166 0.0927 式(34) ${[ {0.03}\;\;{ - 0.02} ]^{\rm{T}}}$ ${[ {0.10}\;\;{ - 0.10} ]^{\rm{T}}}$ 式(39) 0.0092 0.0054 0.0161 0.0770 式(37) ${[ {0.03}\;\;{ - 0.02} ]^{\rm{T}}}$ ${[ {0.10}\;\;{ - 0.10} ]^{\rm{T}}}$ 式(39) 0.0092 0.0054 0.0161 0.0898
下载: 导出CSV
-
[1] Laura M B, Gehrig M D. Orthopedic surgery. The American Journal of Surgery, 2011, 202(3): 364-368 doi: 10.1016/j.amjsurg.2011.06.007 [2] Yen P L, Ho T H. Shared control for a handheld orthopedic surgical robot. IEEE Robotics and Automation Letters, 2021, 6(4): 8394-8400 doi: 10.1109/LRA.2021.3108522 [3] Saeedi-Hosseiny M S, Alruwaili F, McMillan S, Iordachita I, Abedin-Nasab M H. A surgical robotic system for long-bone fracture alignment: Prototyping and cadaver study. IEEE Transactions on Medical Robotics and Bionics, 2022, 4(1): 172-182 doi: 10.1109/TMRB.2021.3129277 [4] Sun T, Lian B B, Yang S F, Song Y M. Kinematic calibration of serial and parallel robots based on finite and instantaneous screw theory. IEEE Transactions on Robotics, 2020, 36(3): 816-834 doi: 10.1109/TRO.2020.2969028 [5] Koessler A, Goldsztejn A, Briot S, Bouton N. Dynamics-based algorithm for reliable assembly mode tracking in parallel robots. IEEE Transactions on Robotics, 2020, 36(3): 937-950 doi: 10.1109/TRO.2020.2987855 [6] Lipiński K. Modeling and control of a redundantly actuated variable mass 3RRR planar manipulator controlled by a model-based feedforward and a model-based-proportional-derivative feedforward-feedback controller. Mechatronics, 2016, 37: 42-53 doi: 10.1016/j.mechatronics.2015.12.002 [7] Sun T, Yang S F. An approach to formulate the hessian matrix for dynamic control of parallel robots. IEEE/ASME Transactions on Mechatronics, 2019, 24(1): 271-281 doi: 10.1109/TMECH.2019.2891297 [8] Liang X, Su T T. Quintic Pythagorean-Hodograph curves based trajectory planning for Delta robot with a prescribed geometrical constraint. Applied Sciences, 2019, 9(21): Article No. 4491 [9] Su T T, Cheng L, Wang Y K, Liang X, Zheng J, Zhang H J. Time-optimal trajectory planning for Delta robot based on quintic Pythagorean-Hodograph curves. IEEE Access, 2018, 6: 28530-28539 doi: 10.1109/ACCESS.2018.2831663 [10] 孔令富, 张世辉, 赵立强, 窦燕. 并联机器人视觉技术及应用. 北京: 机械工业出版社, 2012.Kong Ling-Fu, Zhang Shi-Hui, Zhao Li-Qiang, Dou Yan. Vision Technologies and Application of Parallel Robot. Beijing: China Machine Press, 2012. [11] Shang W W, Cong S. Robust nonlinear control of a planar 2-DOF parallel manipulator with redundant actuation. Robotics and Computer-Integrated Manufacturing, 2014, 30(6): 597-604 doi: 10.1016/j.rcim.2014.04.004 [12] Gomes P. Surgical robotics: Reviewing the past, analysing the present, imagining the future. Robotics and Computer-Integrated Manufacturing, 2011, 27(2): 261-266 doi: 10.1016/j.rcim.2010.06.009 [13] Ghasem A, Sharma A, Greif D N, Alam M, Maaieh M A. The arrival of robotics in spine surgery a review of the literature. SPINE, 2018, 43(23): 1670-1677 doi: 10.1097/BRS.0000000000002695 [14] Lin H, Wang J Q, Han W. Parallel manipulator robot assisted femoral fracture reduction on traction table. In: Proceedings of the 35th International Conference of the IEEE Engineering in Medicine and Biology Society. Osaka, Japan: IEEE, 2013. 4847−4850 [15] Tang P F, Hu L, Du H L, Gong M L, Zhang L H. Novel 3D hexapod computer-assisted orthopaedic surgery system for closed diaphyseal fracture reduction. The International Journal of Medical Robotics and Computer Assisted Surgery, 2012, 8(1): 17-24 doi: 10.1002/rcs.417 [16] Du H L, Hu L, Li C S, Wang T M, Zhao L, Li Y, et al. Advancing computer-assisted orthopaedic surgery using a hexapod device for closed diaphyseal fracture reduction. The International Journal of Medical Robotics and Computer Assisted Surgery, 2015, 11(3): 348-359 doi: 10.1002/rcs.1614 [17] 王豫, 贠超, 张丰全, 杨闯. 双平面导航机器人系统在不同骨科适应症中的应用研究. 机器人, 2007, 29(3): 200-206 doi: 10.3321/j.issn:1002-0446.2007.03.002Wang Yu, Yun Chao, Zhang Feng-Quan, Yang Chuang. Application of the bi-planar navigation robot system in different orthopedic indications. Robot, 2007, 29(3): 200-206 doi: 10.3321/j.issn:1002-0446.2007.03.002 [18] Theodore N, Ahmed A K. The history of robotics in spine surgery. SPINE, 2018, 43(7S): Article No. S23 doi: 10.1097/BRS.0000000000002553 [19] Phillips F M, Lieberman I H, Polly D W J, Wang M Y. Minimally Invasive Spine Surgery: Surgical Techniques and Disease Management (Second edition). New York: Springer, 2014. [20] Ma J H, Sefati S, Taylor R H, Armand M. An active steering hand-held robotic system for minimally invasive orthopaedic surgery using a continuum manipulator. IEEE Robotics and Automation Letters, 2021, 6(2): 1622-1629 doi: 10.1109/LRA.2021.3059634 [21] 周东生. 数字创伤骨科学. 济南: 山东科学技术出版社, 2019.Zhou Dong-Sheng. Digital Traumatic Orthopaedics. Jinan: Shandong Science and Technology Press, 2019. [22] Brandt G, Zimolong A, Carrat L, Merloz P, Staudte H W, Lavallee S, et al. CRIGOS: A compact robot for image-guided orthopedic surgery. IEEE Transactions on Information Technology in Biomedicine, 1999, 3(4): 252-260 doi: 10.1109/4233.809169 [23] Müller A. Consequences of geometric imperfections for the control of redundantly actuated parallel manipulators. IEEE Transactions on Robotics, 2010, 26(1): 21-31 doi: 10.1109/TRO.2009.2035742 [24] Wen H Y, Xu W L, Cong M. Kinematic model and analysis of an actuation redundant parallel robot with higher kinematic pairs for jaw movement. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1590-1598 doi: 10.1109/TIE.2014.2365432 [25] Liang D, Song Y M, Sun T, Dong G. Optimum design of a novel redundantly actuated parallel manipulator with multiple actuation modes for high kinematic and dynamic performance. Nonlinear Dynamics, 2016, 83(1-2): 631-658 doi: 10.1007/s11071-015-2353-1 [26] Su H, Yang C G, Ferrigno G, Momi E D. Improved human-robot collaborative control of redundant robot for teleoperated minimally invasive surgery. IEEE Robotics and Automation Letters, 2019, 4(2): 1447-1453 doi: 10.1109/LRA.2019.2897145 [27] Muller A. Internal preload control of redundantly actuated parallel manipulators-its application to backlash avoiding control. IEEE Transactions on Robotics, 2005, 21(4): 668-677 doi: 10.1109/TRO.2004.842341 [28] Ding B Y, Cazzolato B S, Grainger S, Stanley R M, Costi J J. Active preload control of a redundantly actuated Stewart platform for backlash prevention. Robotics and Computer-Integrated Manufacturing, 2015, 32: 11-24 doi: 10.1016/j.rcim.2014.09.005 [29] Wen S H, Qin G Q, Zhang B W, Lam H K, Zhao Y S, Wang H B. The study of model predictive control algorithm based on the force/position control scheme of the 5-DOF redundant actuation parallel robot. Robotics and Autonomous Systems, 2016, 79: 12-25 doi: 10.1016/j.robot.2016.02.002 [30] Liang X, He G P, Su T T, Wang W Q, Huang C, Zhao Q L, et al. Finite-time observer-based variable impedance control of cable-driven continuum manipulators. IEEE Transactions on Human-Machine Systems, 2022, 52(1): 26-40 doi: 10.1109/THMS.2021.3129708 [31] Dong Y T, Ren B B. UDE-based variable impedance control of uncertain robot systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(12): 2487-2498 doi: 10.1109/TSMC.2017.2767566 [32] Murray R M, Li Z X, Sastry S. A Mathematical Introduction to Robotic Manipulation. Boca Raton: CRC Press, 1994. [33] Cheng H, Yiu Y K, Li Z X. Dynamics and control of redundantly actuated parallel manipulators. IEEE/ASME Transactions on Mechatronics, 2003, 8(4): 483-491 doi: 10.1109/TMECH.2003.820006 [34] Su T T, Niu L Z, He G P, Liang X, Zhao L, Zhao Q L. Coordinated variable impedance control for multi-segment cable-driven continuum manipulators. Mechanism and Machine Theory, 2020, 153: Article No. 103969 doi: 10.1016/j.mechmachtheory.2020.103969 [35] He G P, Fan Y N, Su T T, Zhao L, Zhao Q L. Variable impedance control of cable actuated continuum manipulators. International Journal of Control, Automation, and Systems, 2020, 18(7): 1839-1852 doi: 10.1007/s12555-019-0449-y [36] Kronander K, Billard A. Stability considerations for variable impedance control. IEEE Transactions on Robotics, 2016, 32(5): 1298-1305 doi: 10.1109/TRO.2016.2593492 [37] Slotine J J, Li W P. Applied Nonlinear Control. New Jersey: Prentice Hall, 1991. [38] Cui Y F, Geng Z Q, Zhu Q X, Han Y M. Review: Multi-objective optimization methods and application in energy saving. Energy, 2017, 125: 681-704 doi: 10.1016/j.energy.2017.02.174 [39] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197 doi: 10.1109/4235.996017 [40] 崔志华, 张茂清, 常宇, 张江江, 王晖, 张文生. 基于平均距离聚类的NSGA-II. 自动化学报, 2021, 47(5): 1171-1182Cui Zhi-Hua, Zhang Mao-Qing, Chang Yu, Zhang Jiang-Jiang, Wang Hui, Zhang Wen-Sheng. NSGA-II with average distance clustering. Acta Automatica Sinica, 2021, 47(5): 1171-1182 [41] 王成焘, 苏秀云. 数字骨科学基础. 济南: 山东科学技术出版社, 2019.Wang Cheng-Tao, Su Xiu-Yun. The Basis of Digital Orthopaedics. Jinan: Shandong Science and Technology Press, 2019. [42] Qiao H, Chen J H, Huang X. A survey of brain-inspired intelligent robots: Integration of vision, decision, motion control, and musculoskeletal systems. IEEE Transactions on Cybernetics, 2022, 52(10): 11267-11280 doi: 10.1109/TCYB.2021.3071312 [43] Qiao H, Zhong S L, Chen Z Y, Wang H Z. Improving performance of robots using human-inspired approaches: A survey. Science China Information Sciences, 2022, 65(12): Article No. 221201 doi: 10.1007/s11432-022-3606-1 [44] Su H, Mariani A, Ovur S E, Menciassi A, Ferrigno G, De Momi E. Toward teaching by demonstration for robot-assisted minimally invasive surgery. IEEE Transactions on Automation Science and Engineering, 2021, 18(2): 484-494 doi: 10.1109/TASE.2020.3045655 -
计量
- 文章访问数: 2246
- HTML全文浏览量: 898
- PDF下载量: 356
- 被引次数: 0
