An Overview of Dynamics Analysis and Control of Memristive Neural Networks With Delays
-
摘要: 忆阻器(Memristor)是一种无源的二端电子元件, 同时也是一种纳米级元件, 具有低能耗、高存储、小体积和非易失性等特点. 作为一种新型的存储器件, 忆阻器的研制, 有望使计算机实现人脑特有的信息存储与信息处理一体化的功能, 打破目前冯·诺伊曼(Von Neumann)计算机架构, 为下一代计算机的研制提供一种全新的架构. 鉴于忆阻器与生物神经元突触具有十分相似的功能, 使忆阻器得以充当人工神经元的突触, 建立起一种基于忆阻器的人工神经网络即忆阻神经网络. 忆阻器的问世, 为人工神经网络从电路上模拟人脑提供了可能, 必将极大推动人工智能的发展. 此外, 忆阻神经网络的硬件实现及信号传递过程中, 不可避免会出现时滞与分岔等现象, 因此讨论含各种时滞, 如离散、分布、泄漏时滞以及它们混合的时滞忆阻神经网络系统更具有现实意义. 首先介绍了忆阻器的多种数学模型及其分类, 建立了时滞忆阻神经网络(Delayed memristive neural networks, DMNN)的数学模型并阐述了其优点. 然后提出了处理时滞忆阻神经网络动力学行为与控制问题的两种思路, 详细综述了时滞忆阻神经网络系统的稳定性(镇定)、耗散性与无源性及其同步控制方面的内容, 简述了其他方面的动力学行为与控制, 并介绍了时滞忆阻神经网络动力学行为与控制研究新方向. 最后, 对所述问题进行了总结与展望.Abstract: A memristor is a passive two-terminal electronic element and is also a nanometer element. Meanwhile, it has the features of low-energy consumption, high-storage, small-volume and non-volatility. As a new type of memory device, the memristor has similar characteristics as human brain synapses, which is expected to realize the integration of information storage and processing and breaks through the bottleneck of the current Von Neumann computer architecture, and provides new design architecture for the next generation of computer. Since the distinct characteristic is its memory function, which is very similar to the synapse of biological neurons. In recent years, some researchers have replaced the synaptic connections in neural networks by the memristor, and have established a type of neural networks based on the memristor. In a word, the advent of the memristor makes it possible for artificial neural networks to simulate the human brain, greatly promoting the development of artificial intelligence. In addition, time delays are inevitable in hardware implementations and signal transmission of the memristive neural networks. It is thus crucial to discuss the memristive neural networks with discrete, distributed, leakage and mixed delays. Firstly, this paper introduces numerous kinds of the memristor mathematic models and its classification. We model the delayed memristive neural networks (DMNN) and point out their advantages. Secondly, two ways to deal with the dynamical behaviors and control of the DMNN are provided. The stability (stabilization), passivity and dissipativity, synchronization for the DMNN are elaborated while other dynamical behaviors and control are sketched. New research directions of dynamical behaviors and control of the DMNN are also presented. Finally, a summary and outlook is given.
-
Key words:
- Memristor /
- time-varying delay /
- memristive neural networks /
- dynamical behaviors /
- control
-
表 1 四类忆阻器
Table 1 Four classes of memristors
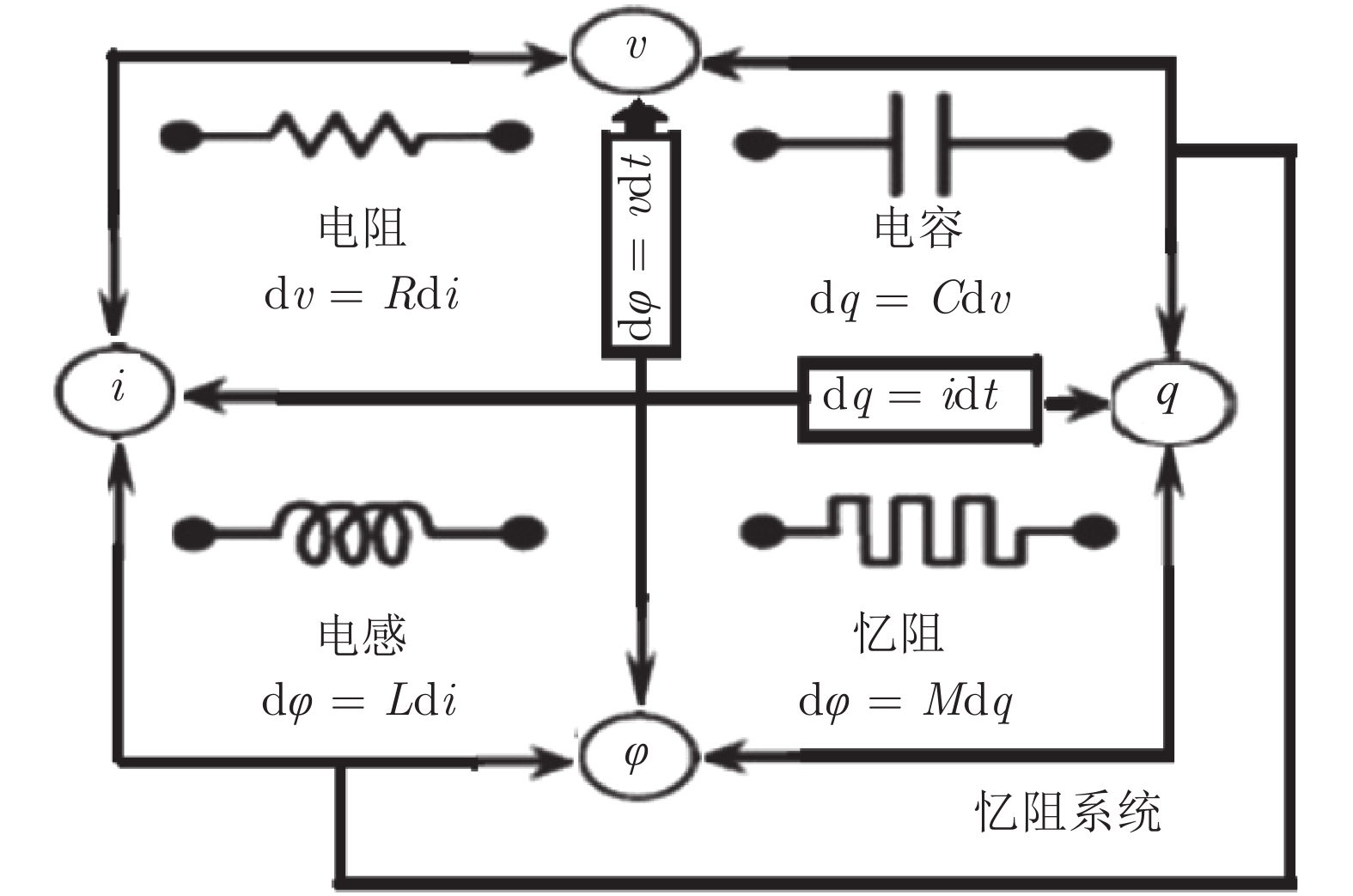
种类 电流控制型 电压控制型 理想型忆阻器 $v = M(q)i$ $i = W(\varphi )v$ $\dfrac{ {{\rm{d}}q} }{ {{\rm{d}}t} } = i$ $\dfrac{ {{\rm{d}}\varphi } }{ {{\rm{d}}t} } = v$ 理想通用型忆阻器 $v = M(x)i$ $i = W(x)v$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = f(x)i$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = g(x)v$ 通用型忆阻器 $v = M(x)i$ $i = W(x)v$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = f(x,i)$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = g(x,v)$ 拓展型忆阻器 $\begin{align} v = M(x,i)i \\ M(x,0) \ne \infty \end{align}$ $\begin{align} i = W(x,v)v \\ W(x,v) \ne 0 \end{align}$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = f(x,i)$ $\dfrac{ {{\rm{d}}x} }{ {{\rm{d}}t} } = g(x,v)$ -
[1] Chua L. Memristor−The missing circuit element. IEEE Transactions on Circuit Theory, 1971, 18(5): 507−519 doi: 10.1109/TCT.1971.1083337 [2] Strukov D B, Snider G S, Stewart D R, Williams R S. The missing memristor found. Nature, 2008, 453(7191): 80−83 doi: 10.1038/nature06932 [3] Tour J M, He T. Electronics: The fourth element. Nature, 2008, 453(7191): 42−43 doi: 10.1038/453042a [4] Borghetti J, Snider G S, Kuekes P J, Yang J J, Stewart D R, Williams R S. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication. Nature, 2010, 464(7290): 873−876 doi: 10.1038/nature08940 [5] Chua L O, Kang S M. Memristive devices and systems. Proceedings of the IEEE, 1976, 64(2): 209−223 doi: 10.1109/PROC.1976.10092 [6] 王小平, 沈轶, 吴计生, 孙军伟, 李薇. 忆阻及其应用研究综述. 自动化学报, 2013, 39(8): 1170−1184Wang Xiao-Ping, Shen Yi, Wu Ji-Sheng, Sun Jun-Wei, Li Wei. Review on memristor and its applications. Acta Automatica Sinica, 2013, 39(8): 1170−1184 [7] Chua L. Everything you wish to know about memristors but are afraid to ask. Radioengineering, 2015, 24(2): 319−368 doi: 10.13164/re.2015.0319 [8] 缪向水, 李祎, 孙华军, 薛堪豪. 忆阻器导论. 北京: 科学出版社, 2018.Miao Xiang-Shui, Li Yi, Sun Hua-Jun, Xue Kan-Hao. Introduction to Memristor. Beijing: Science Press, 2018. [9] Wen S P, Zeng Z G, Huang T W. Dynamic behaviors of memristor-based delayed recurrent networks. Neural Computing and Applications, 2013, 23(3−4): 815−821 doi: 10.1007/s00521-012-0998-y [10] Bartolozzi C, Indiveri G. Synaptic dynamics in analog VLSI. Neural Computation, 2007, 19(10): 2581−2603 doi: 10.1162/neco.2007.19.10.2581 [11] Zhang B Y, Xu S Y, Lam J. Relaxed passivity conditions for neural networks with time-varying delays. Neurocomputing, 2014, 142: 299−306 doi: 10.1016/j.neucom.2014.04.031 [12] Wu A L, Zeng Z G. Lagrange stability of memristive neural networks with discrete and distributed delays. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 690−703 doi: 10.1109/TNNLS.2013.2280458 [13] Wu A L, Zeng Z G. Dynamic behaviors of memristor-based recurrent neural networks with time-varying delays. Neural Networks, 2012, 36: 1−10 doi: 10.1016/j.neunet.2012.08.009 [14] Zhang G D, Shen Y. New algebraic criteria for synchronization stability of chaotic memristive neural networks with time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(10): 1701−1707 doi: 10.1109/TNNLS.2013.2264106 [15] Wu H Q, Han X M, Wang L F, Wang Y, Fang B L. Exponential passivity of memristive neural networks with mixed time-varying delays. Journal of the Franklin Institute, 2016, 353(3): 688−712 doi: 10.1016/j.jfranklin.2015.10.023 [16] Hu J, Wang J. Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays. In: Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona, Spain: IEEE, 2010. 1−8 [17] Guo Z Y, Wang J, Yan Z. Attractivity analysis of memristor-based cellular neural networks with time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 704−717 doi: 10.1109/TNNLS.2013.2280556 [18] Duan S K, Wang H M, Wang L D, Huang T W, Li C D. Impulsive effects and stability analysis on memristive neural networks with variable delays. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(2): 476−481 doi: 10.1109/TNNLS.2015.2497319 [19] Jiang Y L, Li C D. Globally exponential stability of memristive neural networks with time-varying delays and synchronous switching. Acta Automatica Sinica, 2017, 43(8): 1465−1469 [20] Wen S P, Zeng Z G, Huang T W. Exponential stability analysis of memristor-based recurrent neural networks with time-varying delays. Neurocomputing, 2012, 97: 233−240 doi: 10.1016/j.neucom.2012.06.014 [21] Pershin Y V, Di Ventra M. On the validity of memristor modeling in the neural network literature. Neural Networks, 2020, 121: 52−56 doi: 10.1016/j.neunet.2019.08.026 [22] Xiao J Y, Zhong S M. Extended dissipative conditions for memristive neural networks with multiple time delays. Applied Mathematics and Computation, 2018, 323: 145−163 doi: 10.1016/j.amc.2017.11.053 [23] Xiao J Y, Zhong S M, Li Y T. New passivity criteria for memristive uncertain neural networks with leakage and time-varying delays. ISA Transactions, 2015, 59: 133−148 doi: 10.1016/j.isatra.2015.09.008 [24] Xiao J Y, Zhong S M, Li Y T. Improved passivity criteria for memristive neural networks with interval multiple time-varying delays. Neurocomputing, 2016, 171: 1414−1430 doi: 10.1016/j.neucom.2015.07.075 [25] Wang L M, Shen Y. Finite-time stabilizability and instabilizability of delayed memristive neural networks with nonlinear discontinuous controller. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(11): 2914−2924 doi: 10.1109/TNNLS.2015.2460239 [26] Wu A L, Zeng Z G. Algebraical criteria of stability for delayed memristive neural networks. Advances in Difference Equations, 2015, 2015(1): Article No. 111 [27] Aubin J P, Cellina A. Differential Inclusions: Set-Valued Maps and Viability Theory. Berlin Heidelberg: Springer, 1984. [28] Filippov A F. Differential Equations With Discontinuous Righthand Sides. Dordrecht: Kluwer, 1988. [29] Aubin J P, Frankowska H. Set-valued Analysis. Boston: Birkhäuser, 2009. [30] Zhang H G, Wang Z S, Liu D R. A comprehensive review of stability analysis of continuous-time recurrent neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(7): 1229−1262 doi: 10.1109/TNNLS.2014.2317880 [31] Zeng Z G, Zheng W X. Multistability of neural networks with time-varying delays and concave-convex characteristics. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 293−305 doi: 10.1109/TNNLS.2011.2179311 [32] Zhang H G, Shan Q H, Wang Z S. Stability analysis of neural networks with two delay components based on dynamic delay interval method. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(2): 259−267 doi: 10.1109/TNNLS.2015.2503749 [33] Wu Z G, Lam J, Su H Y, Chu J. Stability and dissipativity analysis of static neural networks with time delay. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 199−210 doi: 10.1109/TNNLS.2011.2178563 [34] 钟守铭, 刘碧森, 王晓梅, 范小明. 神经网络稳定性理论. 北京: 科学出版社, 2008.Zhong Shou-Ming, Liu Bi-Sen, Wang Xiao-Mei, Fan Xiao-Ming. Stability Theory of Neural Networks. Beijing: Science Press, 2008. [35] Liao X X, Yu P. Absolute Stability of Nonlinear Control Systems (Second Edition). Dordrecht: Springer, 2008. [36] Tu Z W, Cao J D, Hayat T. Global exponential stability in Lagrange sense for inertial neural networks with time-varying delays. Neurocomputing, 2016, 171: 524−531 doi: 10.1016/j.neucom.2015.06.078 [37] Wang L, Chen T. Multiple μ-stability of neural networks with unbounded time-varying delays. Neural Networks, 2014, 53: 109–118 [38] Li T, Fei S M, Guo Y Q, Zhu Q. Stability analysis on Cohen-Grossberg neural networks with both time-varying and continuously distributed delays. Nonlinear Analysis: Real World Applications, 2009, 10(4): 2600−2612 doi: 10.1016/j.nonrwa.2008.04.003 [39] Shi K B, Zhu H, Zhong S M, Zeng Y, Zhang Y P. Less conservative stability criteria for neural networks with discrete and distributed delays using a delay-partitioning approach. Neurocomputing, 2014, 140: 273−282 doi: 10.1016/j.neucom.2014.03.012 [40] He Y, Liu G P, Rees D. New delay-dependent stability criteria for neural networks with time-varying delay. IEEE Transactions on Neural Networks, 2007, 18(1): 310–314 [41] Arik S. A note on the global stability of dynamical neural networks. IEEE Transactions on Circuits and Systems: I: Fundamental Theory and Applications, 2002, 49(4): 502−504 doi: 10.1109/81.995665 [42] Muralisankar S, Manivannan A, Balasubramaniam P. Mean square delay dependent-probability-distribution stability analysis of neutral type stochastic neural networks. ISA Transactions, 2015: 11–19 [43] Zhang X M, Han Q L. Global asymptotic stability for a class of generalized neural networks with interval time-varying delay. IEEE Transactions on Neural Networks, 2011, 22(8): 1180−1192 doi: 10.1109/TNN.2011.2147331 [44] Zeng H B, He Y, Wu M, Zhang C F. Complete delay-decomposing approach to asymptotic stability for neural networks with time-varying delays. IEEE Transactions on Neural Networks, 2011, 22(5): 806−812 doi: 10.1109/TNN.2011.2111383 [45] Kwon O M, Park M J, Lee S M, Park J H, Cha E J. Stability for neural networks with time-varying delays via some new approaches. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(2): 181−193 doi: 10.1109/TNNLS.2012.2224883 [46] He Y, Wu M, She J H. An improved global asymptotic stability criterion for delayed cellular neural networks. IEEE Transactions on Neural Networks, 2006, 17(1): 250–252 [47] Liang X B, Yamaguchi T. Necessary and sufficient condition for absolute exponential stability of hopfield-type neural networks. IEICE Transactions on Information and Systems E Series D, 1996, 79(7): 990−993 [48] Liao X F, Liu Y B, Guo S T, Mai H H. Asymptotic stability of delayed neural networks: A descriptor system approach. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(7): 3120−3133 doi: 10.1016/j.cnsns.2008.12.001 [49] 段飞腾, 崔宝同. 基于忆阻器时滞神经网络的全局稳定性新判据. 计算机工程, 2015, 41(7): 210−214 doi: 10.3969/j.issn.1000-3428.2015.07.040Duan Fei-Teng, Cui Bao-Tong. New criterion for global stability based on memristor time delay neural network. Computer Engineering, 2015, 41(7): 210−214 doi: 10.3969/j.issn.1000-3428.2015.07.040 [50] Zhang G D, Shen Y, Yin Q, Sun J W. Global exponential periodicity and stability of a class of memristor-based recurrent neural networks with multiple delays. Information Sciences, 2013, 232: 386−396 doi: 10.1016/j.ins.2012.11.023 [51] 胡进, 宋乾坤. 基于忆阻的时滞神经网络的全局稳定性. 应用数学和力学, 2013, 34(7): 724−735 doi: 10.3879/j.issn.1000-0887.2013.07.007Hu Jin, Song Qian-Kun. Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays. Applied Mathematics and Mechanics, 2013, 34(7): 724−735 doi: 10.3879/j.issn.1000-0887.2013.07.007 [52] Mathiyalagan K, Anbuvithya R, Sakthivel R, Park J H, Prakash P. Reliable stabilization for memristor-based recurrent neural networks with time-varying delays. Neurocomputing, 2015, 153: 140−147 doi: 10.1016/j.neucom.2014.11.043 [53] Zhang W, Huang T W, He X, Li C D. Global exponential stability of inertial memristor-based neural networks with time-varying delays and impulses. Neural Networks, 2017, 95: 102−109 doi: 10.1016/j.neunet.2017.03.012 [54] Bao G, Chen Y Y, Wen S Y, Lai Z C. Stability analysis for memristive recurrent neural network and its application to associative memory. Acta Automatica Sinica, 2017, 43(12): 2244−2252 [55] Li R X, Cao J D. Stability analysis of reaction-diffusion uncertain memristive neural networks with time-varying delays and leakage term. Applied Mathematics and Computation, 2016, 278: 54−69 doi: 10.1016/j.amc.2016.01.016 [56] Sheng Y, Lewis F L, Zeng Z G. Exponential stabilization of fuzzy memristive neural networks with hybrid unbounded time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(3): 739−750 doi: 10.1109/TNNLS.2018.2852497 [57] Xiao Q, Zeng Z G. Lagrange stability for T-S fuzzy memristive neural networks with time-varying delays on time scales. IEEE Transactions on Fuzzy Systems, 2018, 26(3): 1091−1103 doi: 10.1109/TFUZZ.2017.2704059 [58] Ding S B, Wang Z S, Rong N N, Zhang H G. Exponential stabilization of memristive neural networks via saturating sampled-data control. IEEE Transactions on Cybernetics, 2017, 47(10): 3027−3029 doi: 10.1109/TCYB.2017.2711496 [59] 王长弘, 王林山. 基于忆阻器的S-分布时滞随机神经网络的均方指数稳定性. 山东大学学报(理学版), 2016, 51(5): 130−135, 142Wang Chang-Hong, Wang Lin-Shan. Mean square exponential stability of memristor-based stochastic neural networks with S-type distributed delays. Journal of Shandong University (Natural Science), 2016, 51(5): 130−135, 142 [60] Sakthivel R, Raja R, Anthoni S M. Exponential stability for delayed stochastic bidirectional associative memory neural networks with Markovian jumping and impulses. Journal of Optimization Theory and Applications, 2013, 158(1): 251−273 doi: 10.1007/s10957-011-9817-3 [61] Li J, Hu M F, Guo L X. Exponential stability of stochastic memristor-based recurrent neural networks with time-varying delays. Neurocomputing, 2014, 138: 92−98 doi: 10.1016/j.neucom.2014.02.042 [62] Meng Z D, Xiang Z R. Stability analysis of stochastic memristor-based recurrent neural networks with mixed time-varying delays. Neural Computing and Applications, 2017, 28(7): 1787−1799 doi: 10.1007/s00521-015-2146-y [63] Cai Z W, Huang L H, Zhu M X, Wang D S. Finite-time stabilization control of memristor-based neural networks. Nonlinear Analysis: Hybrid Systems, 2016, 20: 37−54 doi: 10.1016/j.nahs.2015.12.001 [64] Li R, Cao J. Finite-time stability analysis for Markovian jump memristive neural networks with partly unknown transition probabilities. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 2924−2935 [65] Wang L M, Shen Y, Zhang G D. Finite-time stabilization and adaptive control of memristor-based delayed neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(11): 2648−2659 [66] Sheng Y, Lewis F L, Zeng Z G, Huang T W. Lagrange stability and finite-time stabilization of fuzzy memristive neural networks with hybrid time-varying delays. IEEE Transactions on Cybernetics, 2020, 50(7): 2959−2970 doi: 10.1109/TCYB.2019.2912890 [67] Polyakov A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Transactions on Automatic Control, 2012, 57(8): 2106−2110 doi: 10.1109/TAC.2011.2179869 [68] Wen S P, Zeng Z G, Huang T W, Chen Y R. Passivity analysis of memristor-based recurrent neural networks with time-varying delays. Journal of the Franklin Institute, 2013, 350(8): 2354−2370 doi: 10.1016/j.jfranklin.2013.05.026 [69] Anbuvithya R, Mathiyalagan K, Sakthivel R, Prakash P. Passivity of memristor-based BAM neural networks with different memductance and uncertain delays. Cognitive Neurodynamics, 2016, 10(4): 339−351 doi: 10.1007/s11571-016-9385-1 [70] Fu Q H, Cai J Y, Zhong S M, Yu Y B. Dissipativity and passivity analysis for memristor-based neural networks with leakage and two additive time-varying delays. Neurocomputing, 2018, 275: 747−757 doi: 10.1016/j.neucom.2017.09.014 [71] Cao Y Y, Cao Y T, Wen S P, Huang T W, Zeng Z G. Passivity analysis of delayed reaction-diffusion memristor-based neural networks. Neural Networks, 2019, 109: 159−167 doi: 10.1016/j.neunet.2018.10.004 [72] 张芬, 李智. 基于忆阻时滞神经网络的耗散研究. 工程科学与技术, 2017, 49(3): 129−136Zhang Fen, Li Zhi. Dissipativity research on memristor-based neural networks with time-varying delays. Advanced Engineering Sciences, 2017, 49(3): 129−136 [73] Lee T H, Park M J, Park J H, Kwon O M, Lee S M. Extended dissipative analysis for neural networks with time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(10): 1936−1941 doi: 10.1109/TNNLS.2013.2296514 [74] Jin L, He Y, Jiang L, Wu M. Extended dissipativity analysis for discrete-time delayed neural networks based on an extended reciprocally convex matrix inequality. Information Sciences, 2018, 462: 357−366 doi: 10.1016/j.ins.2018.06.037 [75] Ding S B, Wang Z S, Zhang H G. Dissipativity analysis for stochastic memristive neural networks with time-varying delays: A discrete-time case. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(3): 618−630 doi: 10.1109/TNNLS.2016.2631624 [76] Kwon O M, Park M J, Park J H, Lee S M, Cha E J. Passivity analysis of uncertain neural networks with mixed time-varying delays. Nonlinear Dynamics, 2013, 73(4): 2175−2189 doi: 10.1007/s11071-013-0932-6 [77] Pecora L M, Carroll T L. Synchronization in chaotic systems. Physical Review Letters, 1990, 64(8): 821−824 doi: 10.1103/PhysRevLett.64.821 [78] Wang X F. Complex networks: Topology, dynamics and synchronization. International Journal of Bifurcation and Chaos, 2002, 12(5): 885−916 doi: 10.1142/S0218127402004802 [79] 刘洋, 彭良玉, 董胡. 统一混沌系统同步及其保密通信. 计算机工程与应用, 2008, 44(3): 133−135 doi: 10.3778/j.issn.1002-8331.2008.03.042Liu Yang, Peng Liang-Yu, Dong Hu. Synchronization of unified chaotic system and secure communication. Computer Engineering and Applications, 2008, 44(3): 133−135 doi: 10.3778/j.issn.1002-8331.2008.03.042 [80] 许碧荣. 蔡氏混沌系统网络的混沌同步及其保密通信. 信息与控制, 2010, 39(1): 54−58, 65 doi: 10.3969/j.issn.1002-0411.2010.01.010Xu Bi-Rong. Chaotic synchronization of network of Chua′ s chaotic system and its applications to secure communication. Information and Control, 2010, 39(1): 54−58, 65 doi: 10.3969/j.issn.1002-0411.2010.01.010 [81] Zhang G D, Shen Y. Exponential synchronization of delayed memristor-based chaotic neural networks via periodically intermittent control. Neural Networks, 2014, 55(7): 1−10 [82] Chen W H, Luo S X, Zheng W X. Impulsive synchronization of reaction-diffusion neural networks with mixed delays and its application to image encryption. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(12): 2696−2710 doi: 10.1109/TNNLS.2015.2512849 [83] Chen J J, Zeng Z G, Jiang P. Global Mittag-leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Networks, 2014, 51(3): 1−8 [84] 田小敏, 费树岷, 柴琳. 具有死区输入的分数阶混沌系统的有限时间同步(英文). 控制理论与应用, 2015, 32(9): 1240−1245 doi: 10.7641/CTA.2015.50247Tian Xiao-Min, Fei Shu-Min, Chai Lin. Finite-time synchronization of fractional-order chaotic systems by considering dead-zone phenomenon. Control Theory & Applications, 2015, 32(9): 1240−1245 doi: 10.7641/CTA.2015.50247 [85] Wu H Q, Li R X, Wei H Z, Zhang X W, Yao R. Synchronization of a class of memristive neural networks with time delays via sampled-data control. International Journal of Machine Learning and Cybernetics, 2015, 6(3): 365−373 doi: 10.1007/s13042-014-0271-z [86] Shi Y C, Zhu P Y. Synchronization of memristive competitive neural networks with different time scales. Neural Computing and Applications, 2014, 25(5): 1163−1168 doi: 10.1007/s00521-014-1598-9 [87] Chandrasekar A, Rakkiyappan R, Cao J D, Lakshmanan S. Synchronization of memristor-based recurrent neural networks with two delay components based on second-order reciprocally convex approach. Neural Networks, 2014, 57: 79−93 doi: 10.1016/j.neunet.2014.06.001 [88] Zhang R M, Zeng D Q, Park J H, Zhong S M, Yu Y B. Novel discontinuous control for exponential synchronization of memristive recurrent neural networks with heterogeneous time-varying delays. Journal of the Franklin Institute, 2018, 355(5): 2826−2848 doi: 10.1016/j.jfranklin.2018.01.018 [89] Yang X S, Ho D W C. Synchronization of delayed memristive neural networks: Robust analysis approach. IEEE Transactions on Cybernetics, 2016, 46(12): 3377−3387 doi: 10.1109/TCYB.2015.2505903 [90] Mathiyalagan K, Park J H, Sakthivel R. Synchronization for delayed memristive BAM neural networks using impulsive control with random nonlinearities. Applied Mathematics and Computation, 2015, 259: 967−979 doi: 10.1016/j.amc.2015.03.022 [91] 谢涛. 基于自适应控制的忆阻神经网络同步研究. 西南大学学报(自然科学版), 2018, 40(5): 178−184Xie Tao. Synchronization of memristive neural networks with delays based on adaptive control. Journal of Southwest University (Natural Science Edition), 2018, 40(5): 178−184 [92] Song Y F, Wen S P. Synchronization control of stochastic memristor-based neural networks with mixed delays. Neurocomputing, 2015, 156: 121−128 doi: 10.1016/j.neucom.2014.12.077 [93] 沈君, 楼旭阳. 变时滞随机忆阻器神经网络的同步控制. 计算机系统应用, 2016, 25(4): 23−28Shen Jun, Lou Xu-Yang. Synchronization control of stochastic memristor-based neural networks with time-varying delays. Computer Systems & Applications, 2016, 25(4): 23−28 [94] Abdurahman A, Jiang H J, Teng Z D. Finite-time synchronization for memristor-based neural networks with time-varying delays. Neural Networks, 2015, 69: 20−28 doi: 10.1016/j.neunet.2015.04.015 [95] Cao J D, Li R X. Fixed-time synchronization of delayed memristor-based recurrent neural networks. Science China Information Sciences, 2017, 60(3): Article No. 032201 [96] Wang J Y, Zhang H G, Wang Z S, Gao D W. Finite-time synchronization of coupled hierarchical hybrid neural networks with time-varying delays. IEEE Transactions on Cybernetics, 2017, 47(10): 2995−3004 doi: 10.1109/TCYB.2017.2688395 [97] Jiang M, Wang S, Mei J, Shen Y. Finite-time synchronization control of a class of memristor-based recurrent neural networks. Neural Networks, 2014, 63: 133−140 [98] Haliding X, Jiang H J, Abdurahman A, Hu C. Fixed-time lag synchronization analysis for delayed memristor-based neural networks. Neural Processing Letters, 2020, 52(1): 485−509 doi: 10.1007/s11063-020-10249-0 [99] 王有刚, 武怀勤. 时滞忆阻Cohen-Grossberg神经网络周期解的存在性. 西华大学学报(自然科学版), 2017, 36(5): 22−30, 35 doi: 10.3969/j.issn.1673-159X.2017.05.004Wang You-Gang, Wu Huai-Qin. Existence of periodic solutions for memristive Cohen-Grossberg neural networks with delays. Journal of Xihua University (Natural Science Edition), 2017, 36(5): 22−30, 35 doi: 10.3969/j.issn.1673-159X.2017.05.004 [100] Ding S B, Wang Z S, Wang J D, Zhang H G. H∞ state estimation for memristive neural networks with time-varying delays: The discrete-time case. Neural Networks, 2016, 84: 47−56 doi: 10.1016/j.neunet.2016.08.002 [101] Liu H J, Wang Z D, Shen B, Alsaadi F E. H∞ state estimation for discrete-time memristive recurrent neural networks with stochastic time-delays. International Journal of General Systems, 2016, 45(5): 633−647 doi: 10.1080/03081079.2015.1106731 [102] Rakkiyappan R, Chandrasekar A, Laksmanan S, Park J H. State estimation of memristor-based recurrent neural networks with time-varying delays based on passivity theory. Complexity, 2014, 19(4): 32−43 doi: 10.1002/cplx.21482 [103] Li R X, Gao X B, Cao J D. Non-fragile state estimation for delayed fractional-order memristive neural networks. Applied Mathematics and Computation, 2019, 340: 221−233 doi: 10.1016/j.amc.2018.08.031 [104] Liu H J, Wang Z D, Shen B, Dong H L. Delay-distribution-dependent H∞ state estimation for discrete-time memristive neural networks with mixed time-delays and fading measurements. IEEE Transactions on Cybernetics, 2020, 50(2): 440−451 doi: 10.1109/TCYB.2018.2862914 [105] Xiao M, Zheng W X, Jiang G P, Cao J D. Qualitative analysis and bifurcation in a neuron system with memristor characteristics and time delay. IEEE Transactions on Neural Networks and Learning Systems, 2020, PP(99): 1−15 doi: 10.1109/TNNLS.2020.2995631 [106] 张玮玮, 陈定元, 吴然超, 曹进德. 一类基于忆阻器分数阶时滞神经网络的修正投影同步. 应用数学和力学, 2018, 39(2): 239−248Zhang Wei-Wei, Chen Ding-Yuan, Wu Ran-Chao, Cao Jin-De. Modified projective synchronization of memristor-based fractional-order delayed neural networks. Applied Mathematics and Mechanics, 2018, 39(2): 239−248 [107] Rakkiyappan R, Velmurugan G, Cao J D. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with time delays. Nonlinear Dynamics, 2014, 78(4): 2823−2836 doi: 10.1007/s11071-014-1628-2 [108] Wu A L, Zeng Z G. Global Mittag-Leffler stabilization of fractional-order memristive neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(1): 206−217 doi: 10.1109/TNNLS.2015.2506738 [109] Zhang G D, Zeng Z G, Hu J H. New results on global exponential dissipativity analysis of memristive inertial neural networks with distributed time-varying delays. Neural Networks, 2018, 97: 183−191 doi: 10.1016/j.neunet.2017.10.003 [110] Zhang G D, Hu J H, Zeng Z G. New criteria on global stabilization of delayed memristive neural networks with inertial item. IEEE Transactions on Cybernetics, 2020, 50(6): 2770−2780 doi: 10.1109/TCYB.2018.2889653 [111] Rakkiyappan R, Premalatha S, Chandrasekar A, Cao J D. Stability and synchronization analysis of inertial memristive neural networks with time delays. Cognitive Neurodynamics, 2016, 10(5): 437−451 doi: 10.1007/s11571-016-9392-2 [112] Tu Z W, Cao J D, Alsaedi A, Alsaadi F. Global dissipativity of memristor-based neutral type inertial neural networks. Neural Networks, 2017, 88: 125−133 doi: 10.1016/j.neunet.2017.01.004 [113] Wang J F, Tian L X. Global Lagrange stability for inertial neural networks with mixed time-varying delays. Neurocomputing, 2017, 235: 140−146 doi: 10.1016/j.neucom.2017.01.007 [114] Li N, Zheng W X. Synchronization criteria for inertial memristor-based neural networks with linear coupling. Neural Networks, 2018, 106: 260−270 doi: 10.1016/j.neunet.2018.06.014 [115] Huang D S, Jiang M H, Jian J G. Finite-time synchronization of inertial memristive neural networks with time-varying delays via sampled-date control. Neurocomputing, 2017, 266: 527−539 doi: 10.1016/j.neucom.2017.05.075 [116] Rakkiyappan R, Kumari E U, Chandrasekar A, Krishnasamy R. Synchronization and periodicity of coupled inertial memristive neural networks with supremums. Neurocomputing, 2016, 214: 739−749 doi: 10.1016/j.neucom.2016.06.061 [117] Guo Z Y, Gong S Q, Huang T W. Finite-time synchronization of inertial memristive neural networks with time delay via delay-dependent control. Neurocomputing, 2018, 293: 100−107 doi: 10.1016/j.neucom.2018.03.004 [118] Li X Y, Li X T, Hu C. Some new results on stability and synchronization for delayed inertial neural networks based on non-reduced order method. Neural Networks, 2017, 96: 91−100 doi: 10.1016/j.neunet.2017.09.009 [119] Zhang G D, Zeng Z G. Stabilization of second-order memristive neural networks with mixed time delays via nonreduced order. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(2): 700−706 doi: 10.1109/TNNLS.2019.2910125 [120] Hu X F, Feng G, Duan S K, Liu L. A Memristive multilayer cellular neural network with applications to image processing. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(8): 1889−1901 doi: 10.1109/TNNLS.2016.2552640 [121] Tang Z R, Zhu R H, Hu R H, Chen Y H, Wu E Q, Wang H, et al. A multilayer neural network merging image preprocessing and pattern recognition by integrating diffusion and drift memristors. IEEE Transactions on Cognitive and Developmental Systems, 2020, PP(99): 1−1 doi: 10.1109/TCDS.2020.3003377 [122] Yang L, Zeng Z G, Huang Y, Wen S P. Memristor-based circuit implementations of recognition network and recall network with forgetting stages. IEEE Transactions on Cognitive and Developmental Systems, 2018, 10(4): 1133−1142 doi: 10.1109/TCDS.2018.2859303 [123] Wen S P, Xie X D, Yan Z, Huang T W, Zeng Z G. General memristor with applications in multilayer neural networks. Neural Networks, 2018, 103: 142−149 doi: 10.1016/j.neunet.2018.03.015 [124] Zhang Y, Wang X P, Friedman E G. Memristor-based circuit design for multilayer neural networks. IEEE Transactions on Circuits and Systems I: Regular Papers, 2018, 65(2): 677−686 doi: 10.1109/TCSI.2017.2729787 [125] Wen S P, Xiao S X, Yang Y, Yan Z, Zeng Z G, Huang T W. Adjusting learning rate of memristor-based multilayer neural networks via fuzzy method. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(6): 1084−1094 doi: 10.1109/TCAD.2018.2834436 [126] Song Y D, Wang Y J, Wen C Y. Adaptive fault-tolerant PI tracking control with guaranteed transient and steady-state performance. IEEE Transactions on Automatic Control, 2017, 62(1): 481−487 doi: 10.1109/TAC.2016.2554362 [127] Song Y D, Huang X C, Wen C Y. Tracking control for a class of unknown nonsquare MIMO nonaffine systems: A deep-rooted information based robust adaptive approach. IEEE Transactions on Automatic Control, 2016, 61(10): 3227−3233 doi: 10.1109/TAC.2015.2508741 [128] Wang Y J, Song Y D, Krstic M, Wen C Y. Fault-tolerant finite time consensus for multiple uncertain nonlinear mechanical systems under single-way directed communication interactions and actuation failures. Automatica, 2016, 63: 374−383 doi: 10.1016/j.automatica.2015.10.049 [129] Song Y D, Wang Y J, Holloway J, Krstic M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica, 2017, 83: 243−251 doi: 10.1016/j.automatica.2017.06.008 -




 下载:
下载: