Research on 3D Point Cloud Skeleton Extraction Based on Improved Adaptive k-means Clustering
-
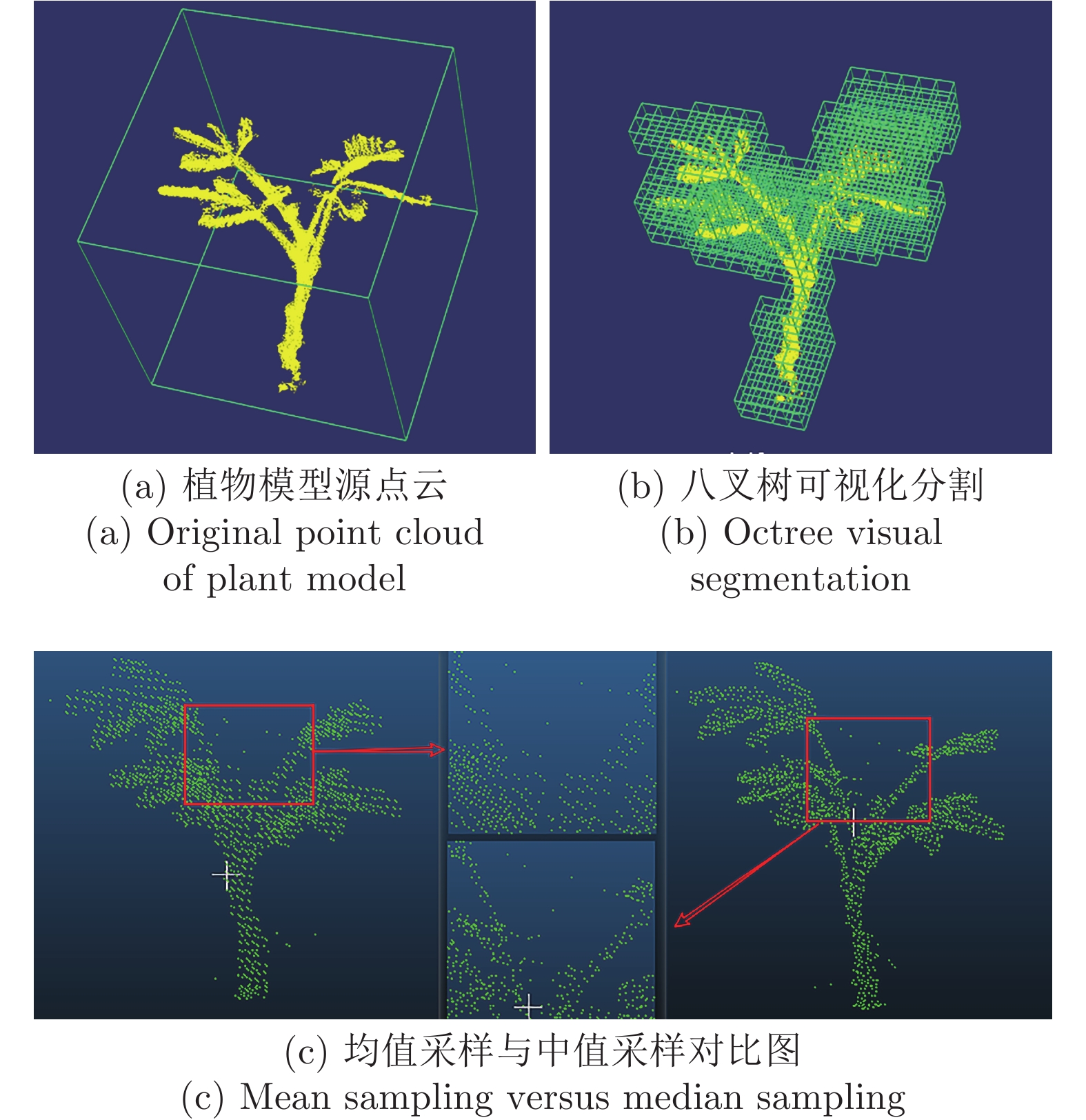
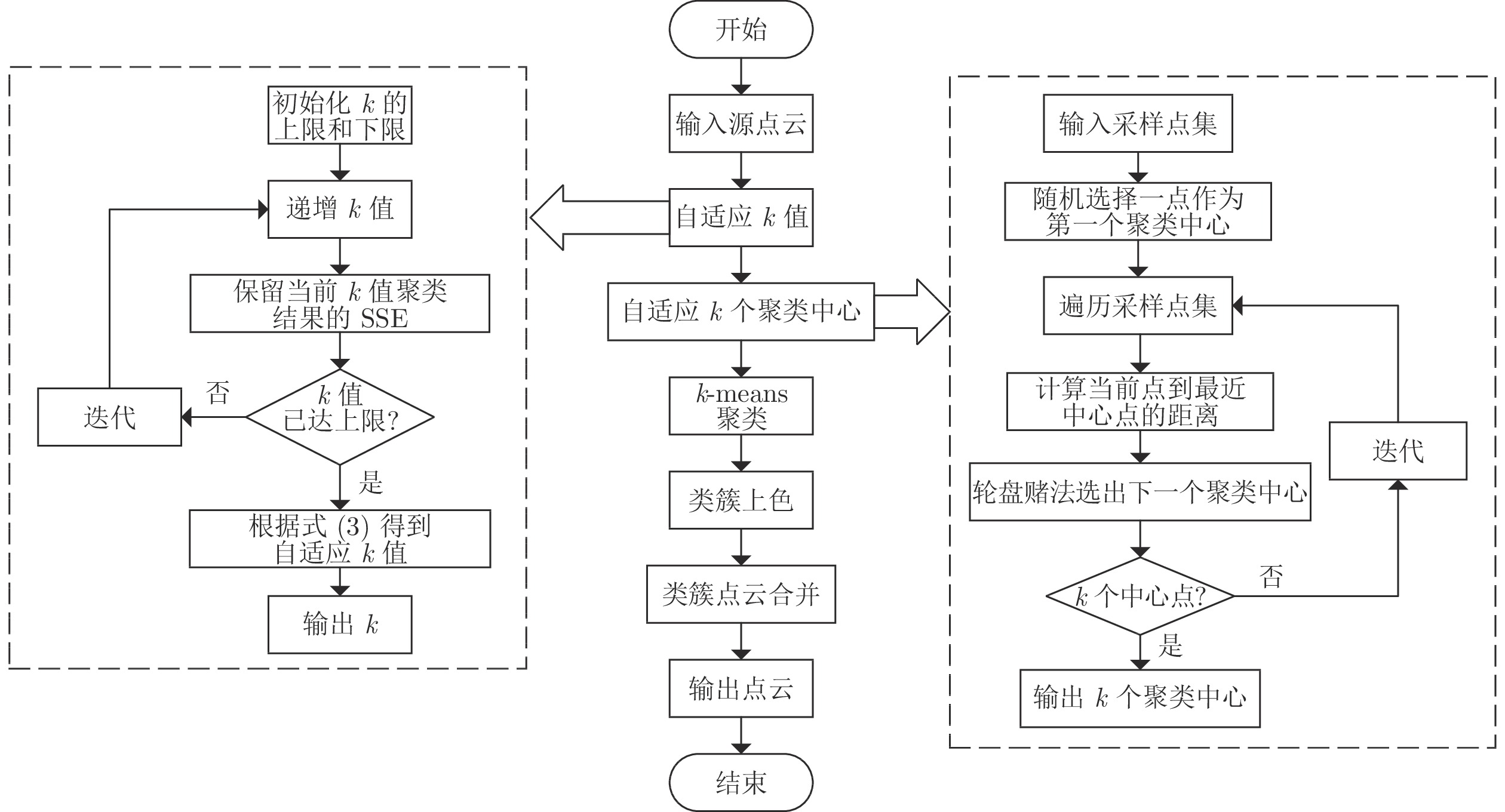
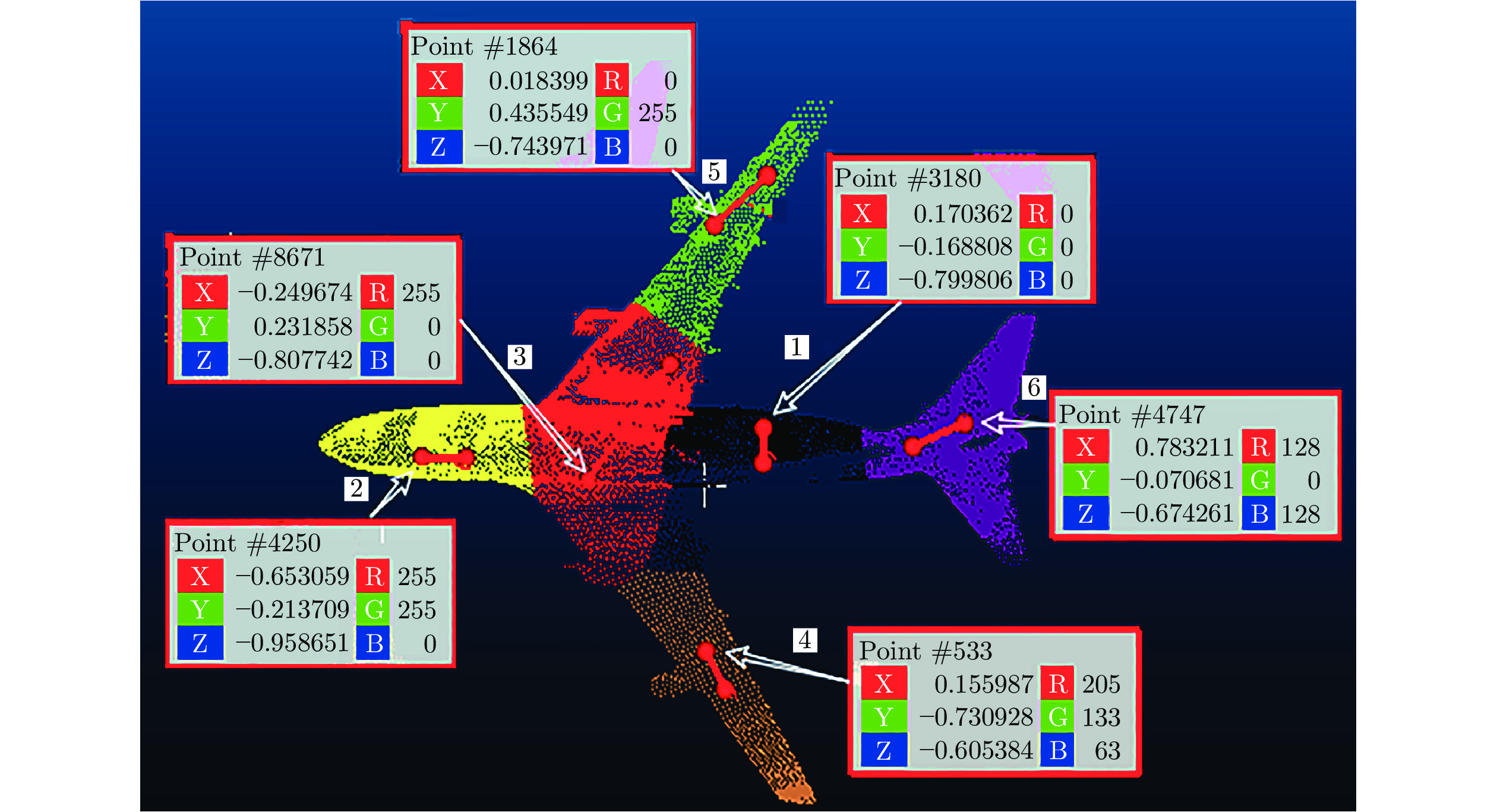
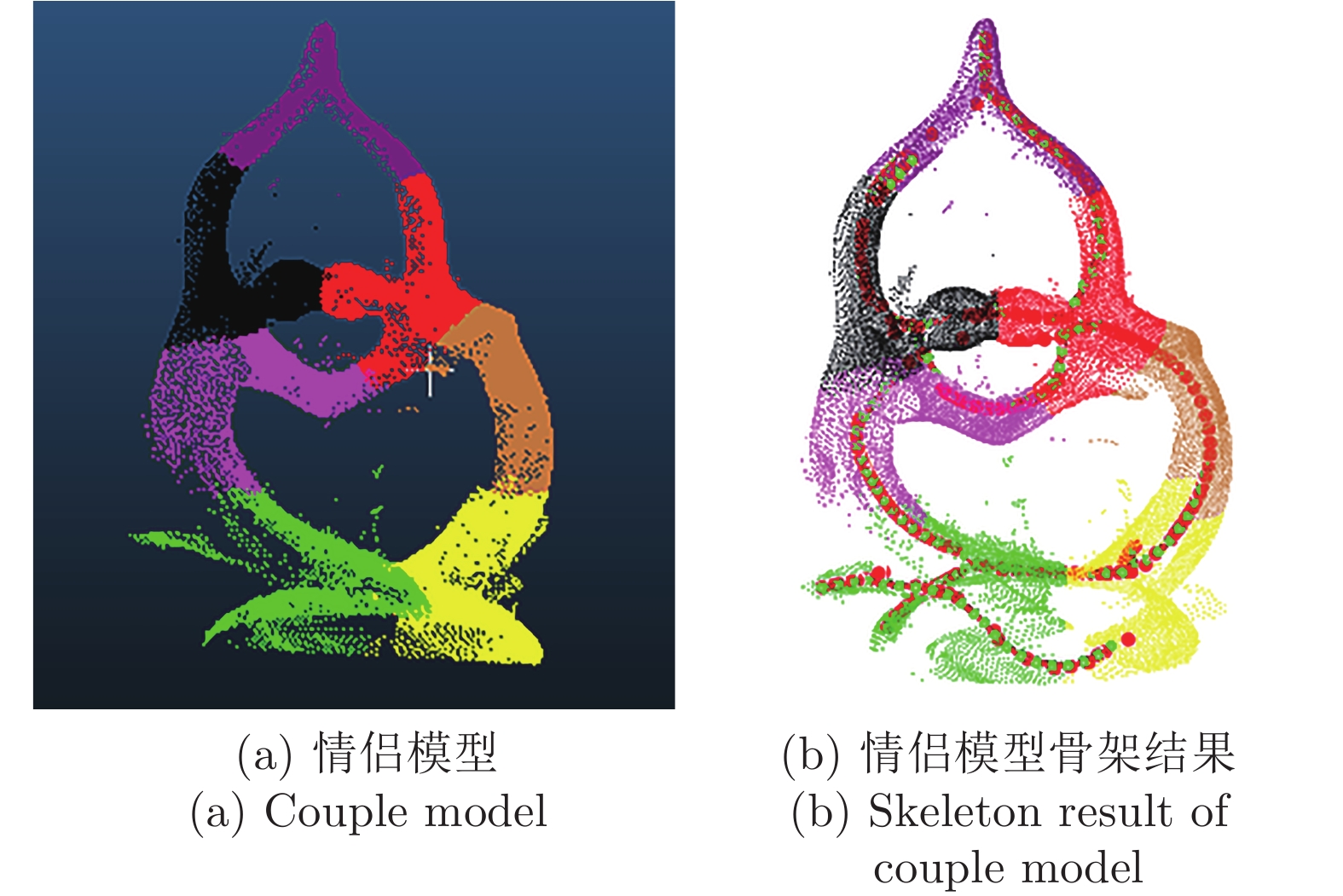
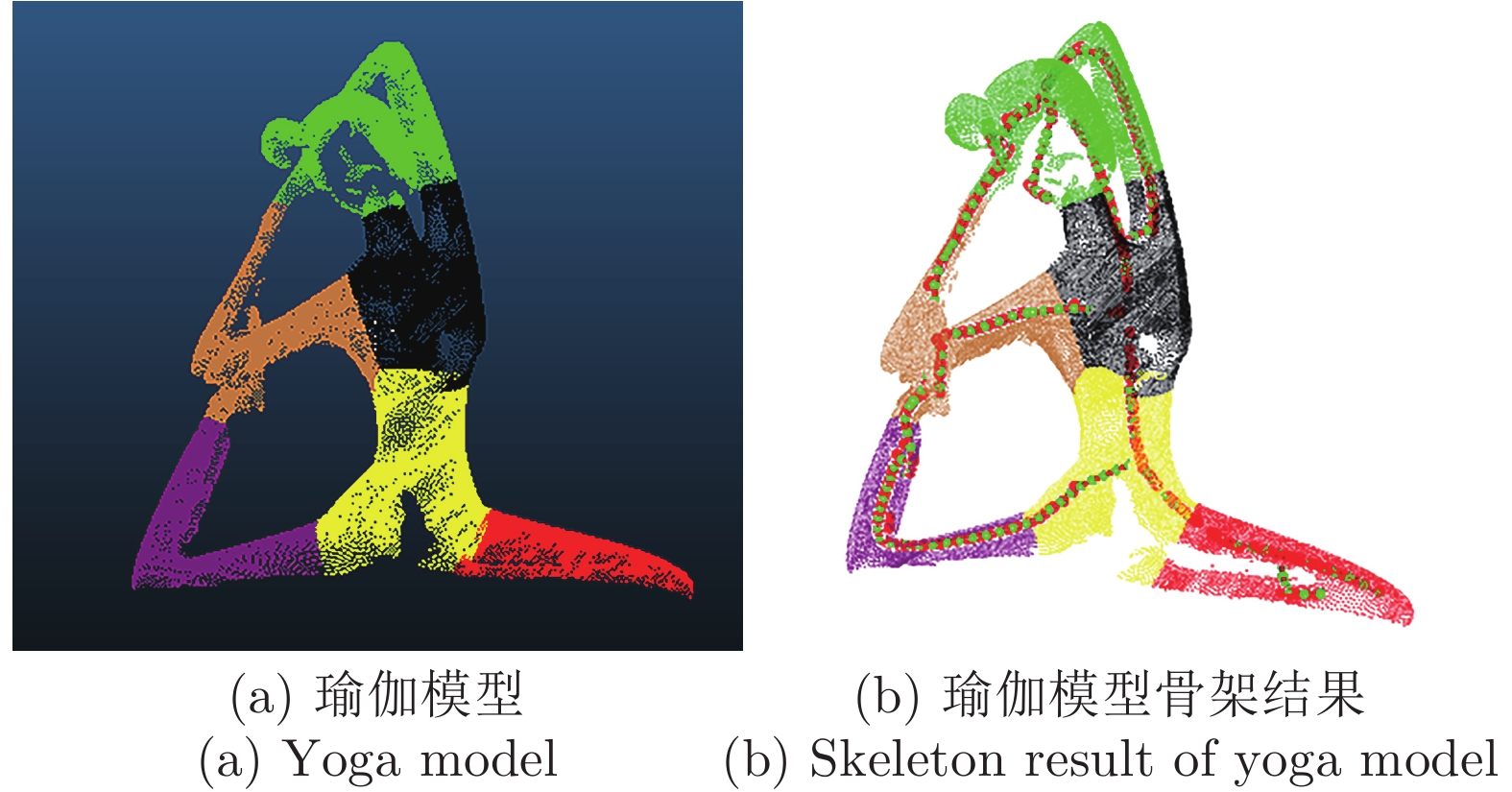
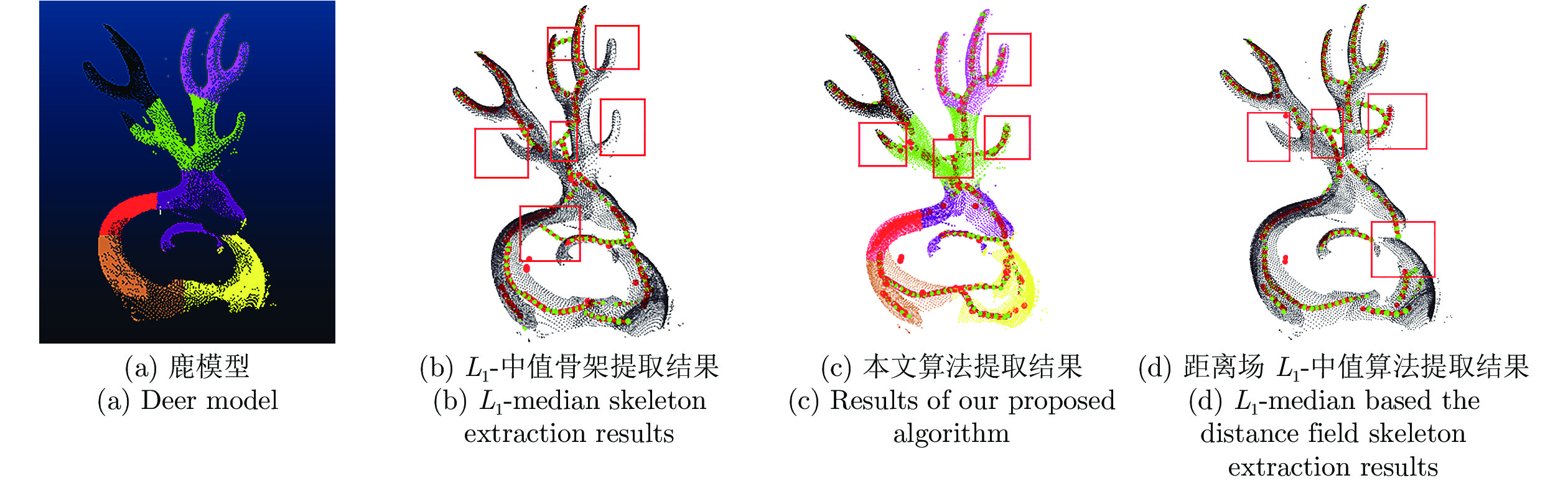
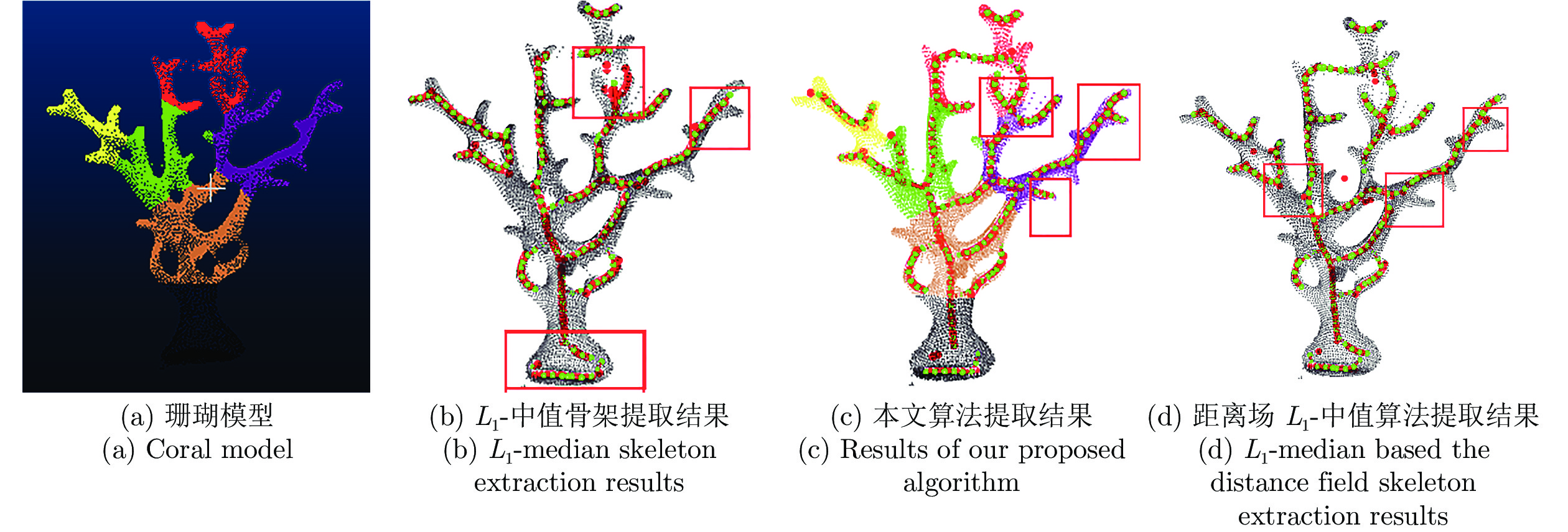
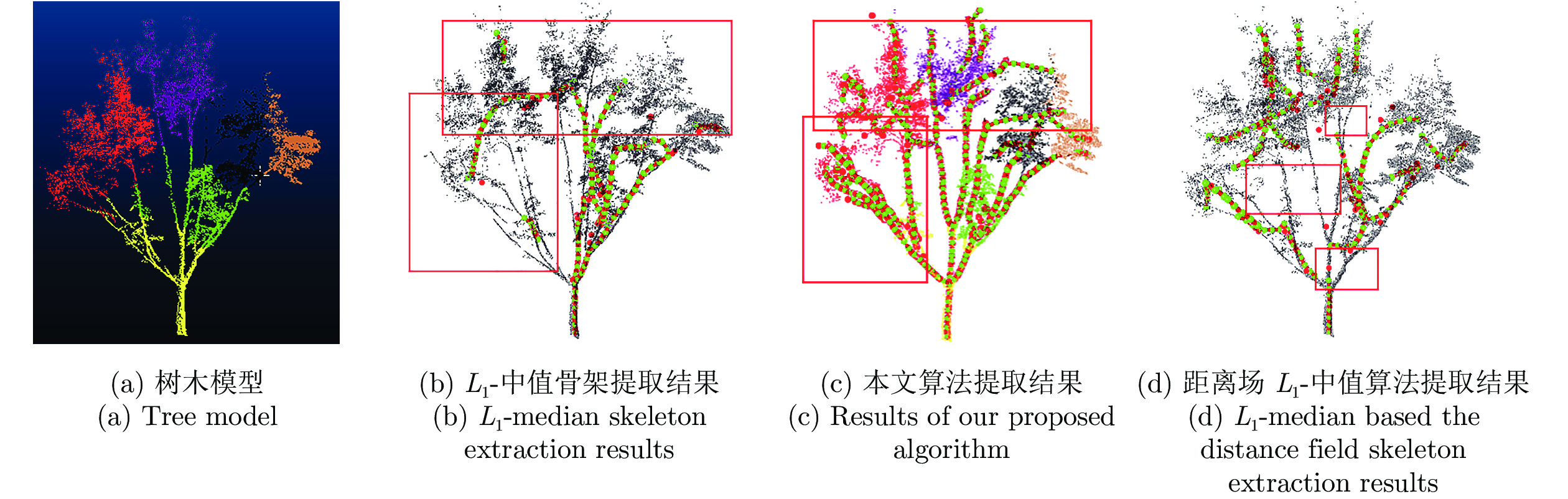
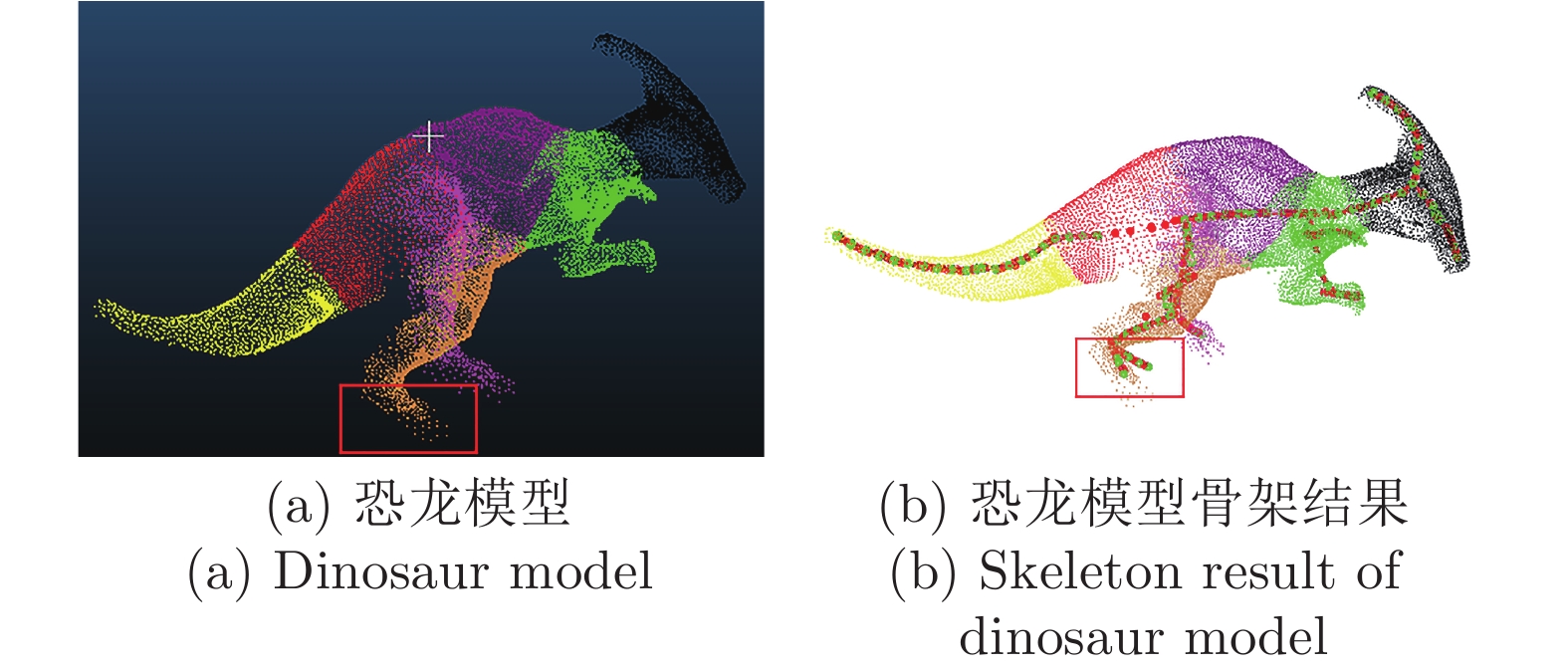
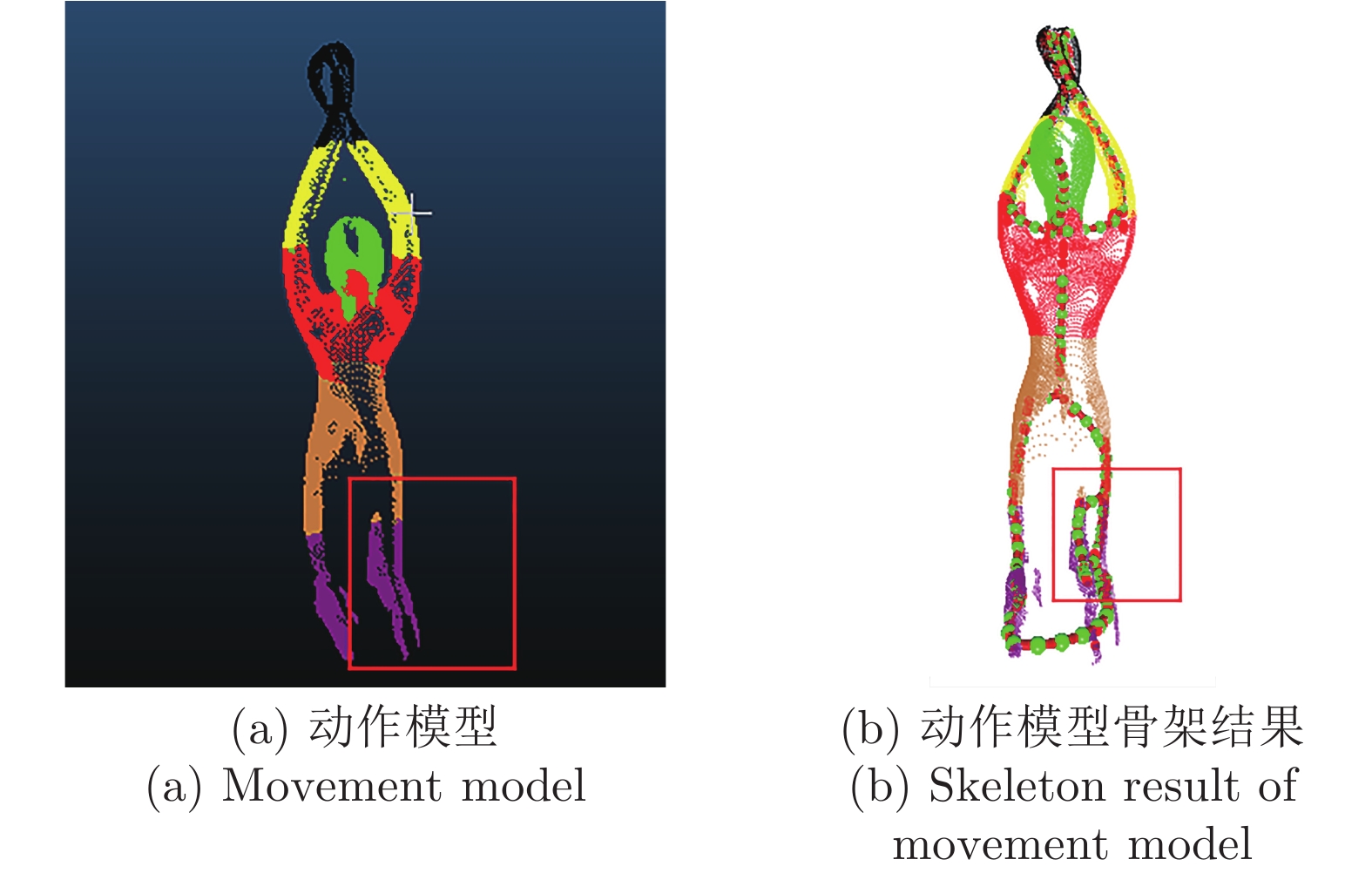
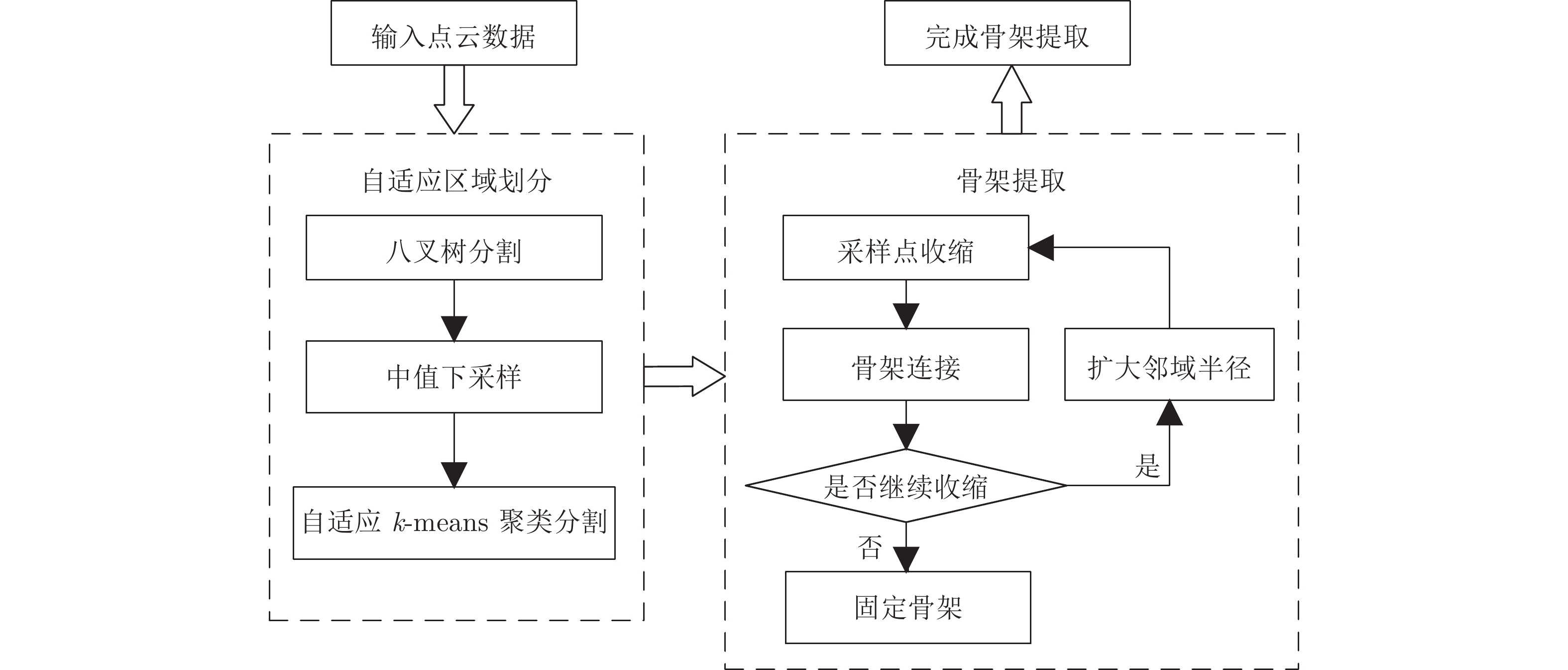
摘要: 针对三维点云中心骨架提取问题, 提出一种基于改进的自适应k均值聚类预分割引导的点云骨架提取算法. 首先, 将输入点云体素化, 利用八叉树算法覆盖输入点云并下采样实现点云化简; 其次, 在采样点中自适应选取初始聚类中心对点云进行区域划分, 并颜色标记; 最后, 在区域分割的引导下应用L1-中值骨架提取算法实现点云骨架的提取. 该算法主要针对L1-中值算法可重复性差、易丢失细节等缺点进行了改进, 并且对输入点云的质量以及形状的几何或拓扑信息, 都没有严格的先验要求, 可以直接应用到未经任何预处理、含有噪声或离群点的初始扫描点云上. 展示了从多种不规则点云提取的骨架结果, 包括矮小植物、人体动作等. 与传统算法相比, 该算法具有高准确率、强鲁棒性、强学习扩展能力等优点.Abstract: Aiming at the extraction problem of three-dimensional point cloud center skeleton, a point cloud skeleton extraction algorithm based on improved adaptive k-means clustering pre-segmentation guidance is proposed. Firstly, the input point cloud was voxelized and the octree algorithm was used to cover the input point cloud and to simplify the point cloud. Secondly, the initial clustering center is selected adaptively from the sampling points to divide the region of the point cloud, and the color is marked. At last, under the guidance of region segmentation, L1-medial skeleton extraction algorithm is applied to extract the point cloud skeleton. This algorithm is mainly aimed at the poor repeatability of L1-median algorithm, easy to lose details and other shortcomings, and there are no strict prior requirements for the quality and geometric or topological information of the input point cloud, which can be directly applied to the initial scanning point cloud without any preprocessing, containing noise or outliers. This paper presents the results of skeleton extracted from a variety of irregularly shaped point clouds, including dwarf plants and human movements. Compared with the traditional algorithm, this algorithm has the advantages of high accuracy, strong robustness and strong learning and expansion ability.
-
Key words:
- Skeleton extraction /
- adaptive clustering /
- L1-median algorithm /
- octree sampling /
- region guided
-
图 2 2011 ~ 2019年点云骨架提取方向论文发表年度趋势图
Fig. 2 Annual trend chart of the paper published in the point cloud skeleton extraction field from 2011 to 2019
图 8 初始中心位置导致分类结果不同
Fig. 8 The initial center position results in different classification results
图 11 飞机点云自适应k均值聚类的分割结果
Fig. 11 Adaptive k-means segmentation results of aircraft point cloud
图 18 鹿模型的点云骨架提取对比结果
Fig. 18 Comparison results of point cloud skeleton extraction of deer model
图 19 珊瑚模型的点云骨架提取对比结果
Fig. 19 Comparison results of point cloud skeleton extraction of coral model
图 20 树木模型的点云骨架提取对比结果
Fig. 20 Comparison results of point cloud skeleton extraction of tree model
表 1 三维点云骨架提取方法的比较
Table 1 Comparison of three-dimensional point cloud skeleton extraction methods
骨架提取方法 代表性文章 关键点 优点 缺点 距离变换法 Zhou 等[17]提出了一种基
于距离场对三维模型
体素化编码的方法将连续的中间点连接为
体素路径, 经过细化、
平滑操作得到骨架计算简单, 且对边界
复杂性不敏感离散域中得到的骨
架往往不连续Song 等[18]提出了一种基于
距离场引导的L1-中值骨
架提取算法利用距离场多尺度参数细
化方法提取初始骨架, 之后
引入 L1-中值算法进行骨架优化利用距离场得到的初始
骨架可有效地引导 L1-中值
算法采样点的移动, 且弥补
了骨架不连续的缺点对于大面积缺失的点云
提取效果很差, 另外计算
距离场时间复杂度高Hu 等[19]提出了一种通过距
离场和曲率结合捕获特
征点的三维点云曲线骨
架提取算法为 3D 点云模型提供距离
场的替代, 通过特征点移
动和聚类形成骨架对于数据缺失严重的点云
模型, 仍能很好的保持骨架
的中心性, 不产生虚假分支对于表面平坦的模型,
特征点容易被识别错误,
从而导致错误骨架Laplace 收缩法 Cao 等[20]提出了一种基于
Laplace 算子的收缩提取
曲线骨架的算法通过局部 Delaunay 三角
剖分和拓扑细化来处理点
云, 从外向内迭代收缩从
而提取骨架具有强大的抗噪能力, 可以
处理丢失少量数据的点云易在局部点云上出现过收
缩, 骨架准确性严重依
赖于 Laplace 算子参数Erdal 等[21]提出了一种将
Laplace 收缩与 L1-中值收
缩相结合的算法在 Laplace 迭代收缩后的
点云上应用L1-中值骨
架提取算法两种方法的收缩过程都是基
于点的邻域完成的, 实现了
优势互补, 减少了迭代次数参数设置不准确, 极
易产生错误骨架Wu 等[22]提出了一种基于改
进 Laplace 实现玉米植株
点云骨架提取的算法应用并改进了Laplace骨架
提取方法, 并通过自适应采样
选择骨架关键点, 相邻点连接
形成植物骨架.能够准确提取植物骨架,
能够逼近植株器官的几
何中心, 如叶脉和茎的中轴骨架结果严重依赖于
扫描点云的质量广义旋转对
称轴法Tagliasacchi 等[23]提出了
ROSA 法来实现模型骨
架的提取基于模型的旋转对称性,
利用邻域内点的法向量垂
直环绕于中轴伸长方
向提取骨架对于大面积缺失的多分支
点云, 提取的骨架仍能正确
的表示原始模型的拓扑结构过多的预处理极大地增
加了时间复杂度, 多用
于圆柱形模型Jayadevan 等[24]提出了一种
形状分解的方法对三维
点云模型进行骨架提取充分运用通用圆柱体的
平移对称属性对三维点云模
型进行形状分解, 分别提取
骨架再进行连接可以很好地处理平面点云,得
到直线骨架; 可通过可视化
调整参数以得到更好的效果骨架连接有时较为死
板, 导致不自然的骨架Fu 等[25]提出了一种利用
圆柱形先验约束优化
提取骨架的算法通过八叉树和水平集方法
提取初始骨架点, 之后采用
圆柱形先验约束优化来提
高骨架的中心性使用关于树枝半径的先验
知识来改进关节点的不正确
定位, 有效的提高了拓扑正
确性和树骨架的中心性专门为树点云设计, 无法
拓展到其他类型的点云空间中轴法 Huang 等[11]提出了基于
L1-中值实现骨架提
取的算法对点云应用局部中值提
取初始骨架, 通过不断扩
大邻域半径达到针对不同
区域实现不同程度收缩的目的可以在原始扫描数据上进行
操作, 即不需要任何预处理采样敏感, 且参数的设置
对骨架提取结果影响大Su 等[26]提出一种基于分
类枝叶和枝干的树
木骨架提取方法通过分类和分割方法将叶子和
木材成分分离, 之后采用 L1-中
值算法精确提取树骨架点充分利用了树木叶片和枝干
在结构及几何特征上的差
异, 提取的骨架在形态上与
树的点云具有良好的一致性由于树叶的遮挡作用, 提
取的骨架是不连续的Mei 等[27]提出一种 L1-MST
算法优化提取树骨架利用 L1-中值提取粗骨架, 基于
点的主导方向和局部点密度的
迭代优化过程实现数据补全,
结合最小生成树法细化骨架L1-MST 算法弥补了L1-中值
算法中因无法准确描述点的
局部空间分布导致错误骨架
连接的缺点数据补全只能用于可见区
域, 因此不能提取被遮挡
区域的骨架
下载: 导出CSV
表 2 不同模型的实验结果对比
Table 2 Comparison table of experimental results of different models
模型 模型点数目 分割区域数 采样点数 本文算法
迭代次数L1-骨架提取算
法迭代次数本文算法运行
时间 (秒)L1-骨架提取算法
运行时间 (秒)鹿模型 22 568 7 6 128 180 275 16 21 情侣模型 43 545 7 9 222 241 301 39 58 人像模型 44 230 5 3 625 161 198 38 44 瑜伽模型 70 457 6 8 909 193 243 26 39 灯罩模型 30 065 9 15 986 186 267 31 43 树木模型 22 698 6 7 849 169 290 19 23
下载: 导出CSV
-
[1] 金朝勇, 耿国华, 李姬俊男, 周明全, 朱新懿. 一种新的虚拟血管镜自动导航路径生成方法. 自动化学报, 2015, 41(8): 1412-1418JIN Chao-Yong, GENG Guo-Hua, LI Ji-Jun-Nan, ZHOU Ming-Quan, ZHU Xin-Yi. A New Automatic Navigation Path Generation Approach to Virtual Angioscopy. ACTA AUTOMATICA SINICA, 2015, 41(8): 1412-1418 [2] 张义宽, 张晓鹏, 查红彬, 张讲社. 三维点云的拓扑结构表征与计算技术. 中国图象图形学报, 2008, 13(8): 1576-1587 doi: 10.11834/jig.20080832Zhang Yi-Kuan, Zhang Xiao-Peng, Zha Hong-Bin, Zhang Jiang-She. A survey of topologically structural representation and computation of 3D point cloud data. Journal of Image and Graphics, 2008, 13(8): 1576-1587 doi: 10.11834/jig.20080832 [3] Gagnier P Y, Maschner H, Gailliegue A, Norgeot L, Abourachid A. Automatic reconstruction of polygon triangulation for mounted skeleton point cloud. In: Proceedings of the IEEE International Conference on E-science. Auckland, New Zealand: 2017. 528−532 [4] 李仁忠, 刘哲闻, 刘阳阳. 基于点云内骨架的分割算法. 自动化学报激光与光电子学进展, 2019, 56(22)Li Ren-Zhong, Liu Zhe-Wen, Liu Yang-Yang. Segmentation algorithm based on point cloud skeleton. Laser&Optoelectronics Progress, 2019, 56(22) [5] Jiang Wei, Xu Kai, Cheng Zhi-Quan, Martin R R, Dang Gang. Curve skeleton extraction by coupled graph contraction and surface clustering. Graphical Models, 2013, 75(3): 137-148 doi: 10.1016/j.gmod.2012.10.005 [6] Shen W, Zhao K, Jiang Y, Wang Y, Zhang Z Z, Bai X. Object skeleton extraction in natural iby fusing scale-associated deep side outputs. In: Proceedings of the Computer Vision and Pattern Recognition. Las Vegas, NV, USA: 2016. 222−230 [7] 徐思雨, 祝继华, 田智强, 李垚辰, 庞善民. 逐步求精的多视角点云配准方法. 自动化学报, 2019, 45(8): 1486-1494XU Si-Yu, ZHU Ji-Hua, TIAN Zhi-Qiang, LI Yao-Chen, PANG Shan-Min. Stepwise Refinement Approach for Registration of Multi-view Point Sets. ACTA AUTOMATICA SINICA, 2019, 45(8): 1486-1494 [8] Noh S T, Takahashi K, Adachi M, Igarashi T. Shape refinement and rigging of raw-scanned 3D volume by a user-specified skeleton. Computers & Graphics, 2020, 87: 80-88 [9] Alwaely B, Abhayaratne C. Adaptive graph formulation for 3D shape representation. In: Proceedings of the International Conference on Acoustics Speech and Signal Processing. Brighton, UK: IEEE, 2019. 1947−1951 [10] Lu W, Zhang X, Liu Y. L1-medial skeleton-based 3D point cloud model retrieval. Multimedia Tools and Applications, 2019, 78(1): 479-488 doi: 10.1007/s11042-017-5136-5 [11] Huang H, Wu S H, Cohen-Or D, Gong M L, Zhang H, Li G Q, Chen B Q. L1-medial skeleton of point cloud. ACM Transactions on Graphics, 2013, 32(4): 96 [12] Blum H. A transformation for extracting new descriptors of shape. Models for the Perception of Speech and Visual Form, 1967: 362-380 [13] Dey T K, Sun J. Defining and computing curve-skeletons with medial geodesic function. Symposium on Geometry Processing, 2006: 143-152 [14] Cornea N D, Silver D, Min P. Curve-skeleton properties, applications, and algorithms. IEEE Transactions On Visualization and Computer Graphics, 2007, 13(3): 530-548 doi: 10.1109/TVCG.2007.1002 [15] Au O K C, Tai C L, Chu H K, Cohen-Or D, Lee T Y. Skeleton extraction by mesh contraction. ACM Transactions on Graphics, 2008, 27(3): 44 [16] Small C G. A Survey of Multidimensional Medians. International Statistical Review, 1990, 58(3): 263-277 doi: 10.2307/1403809 [17] Zhou Y, Toga A W. Efficient Skeletonization of volumetric objects. IEEE Transactions On Visualization and Computer Graphics, 1999, 5(3): 196-209 doi: 10.1109/2945.795212 [18] Song C, Pang Z, Jing X, Xiao C. Distance field guided L1-median skeleton extraction. The Visual Computer, 2018, 34(2): 243-255 doi: 10.1007/s00371-016-1331-z [19] Hu H, Li Z, Jin X, Deng Z, Shen Y. Curve skeleton extraction from 3D point clouds through hybrid feature point shifting and clustering. Computer Graphics Forum, 2020 [20] Cao J, Tagliasacchi A, Olson M, Zhang H, Su Z. Point cloud skeletons via laplacian based contraction. In: Proceedings of the 2010 Shape Modeling International Conference. Provence, France: 2010. 187−197 [21] Erdal O, Ahmet C, Zafer G. A hybrid method for skeleton extraction on kinect sensor data: combination of L1-median and laplacian shrinking algorithms. Measurement, 2018: 535-544 [22] Wu S, Wen W, Xiao B, Guo X, Du J, Wang C, et al. An accurate skeleton extraction approach from 3D point clouds of maize plants. Frontiers in Plant Science, 2019, 10: 248 doi: 10.3389/fpls.2019.00248 [23] Tagliasacchi A, Zhang H, Cohen-Or D. Curve skeleton extraction from incomplete point cloud. ACM Transactions on Graphics, 2009, 28(3): 71 [24] Jayadevan V, Delp E J, Pizlo Z. Skeleton extraction from 3D point clouds by decomposing the object into parts. arXiv perprint, 2019, arXiv.1912.11932 [25] Fu L, Liu J, Zhou J, Zhang M, Lin Y. Tree Skeletonization for Raw Point Cloud Exploiting Cylindrical Shape Prior. IEEE Access, 2020: 27327-27341 [26] Su Z, Li S, Liu H, He Z. Tree skeleton extraction from laser scanned points. In: Proceedings of the 2019 International Geoscience and Remote Sensing Symposium. Yokohama, Japan: IEEE, 2019. 6091−6094 [27] Mei J, Zhang L, Wu S, Wang Z, Zhang L. 3D tree modeling from incomplete point clouds via optimization and L1-MST. International Journal of Geographical Information Science, 2017, 31(5): 999-1021 doi: 10.1080/13658816.2016.1264075 [28] 梁周雁, 赵富燕, 孙文潇, 邵为真. 基于三维激光扫描技术的地表变形监测方法研究. 测绘与空间地理信息, 2017, 40(6): 213-216, 219 doi: 10.3969/j.issn.1672-5867.2017.06.070Liang Zhou-Yan, Zhao Fu-Yan, Sun Wen-Xiao, Shao Wei-Zhen. The research of surface deformation monitoring method using 3D laser scanning technique. Geomatics and Spatial Information Technology, 2017, 40(6): 213-216, 219 doi: 10.3969/j.issn.1672-5867.2017.06.070 [29] Ji S, Shi H. K-means clustering optimization algorithm for massive data. Computer Engineering and Application, 2014, 14: 143-147 [30] Arthur D, Vassilvitskii S. K-means++: The advantages of careful seeding. In: Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms. New Oreans, Louisiana, USA: ACM, 2007. 1027−1035 [31] 庞旭芳, 庞明勇, 肖春霞. 点云模型谷脊特征的提取与增强算法. 自动化学报, 2010, 36(8): 1073-1083 doi: 10.3724/SP.J.1004.2010.01073PANG Xu-Fang, PANG Ming-Yong, XIAO Chun-Xia. An Algorithm for Extracting and Enhancing Valley-ridge Features from Point Sets. ACTA AUTOMATICA SINICA, 2010, 36(8): 1073-1083 doi: 10.3724/SP.J.1004.2010.01073 [32] Li G, Ma W, Bao H. A New Interpolatory Subdivision for Quadrilateral Meshes. Computer Graphics Forum, 2005, 24(1): 3-16 doi: 10.1111/j.1467-8659.2005.00824.x [33] Gander W, Golub G H, Strebel R. Least-squares Fitting of Circles and Ellipses. Bit Numerical Mathematics, 1994, 34(4): 558-578 doi: 10.1007/BF01934268 -
图(22) / 表(2)
计量
- 文章访问数: 2085
- HTML全文浏览量: 780
- PDF下载量: 345
- 被引次数: 0
