区间二型模糊集和模糊系统: 综述与展望

伍冬睿; 曾志刚; 莫红; 王飞跃

doi:10.16383/j.aas.c200133

区间二型模糊集和模糊系统: 综述与展望

doi: 10.16383/j.aas.c200133

1.
华中科技大学人工智能与自动化学院图像信息处理与智能控制教育部重点实验室武汉 430074
2.
长沙理工大学电气与信息工程学院长沙 410114
3.
中国科学院自动化研究所复杂系统管理与控制国家重点实验室北京 100190

基金项目: 国家自然科学基金(61873321, U1913207), 湖北省技术创新专项资助项目(2019AEA171), NSFC-深圳机器人基础研究中心重点项目(U1913207), 科技部政府间国际科技创新合作重点专项(2017YFE0128300)资助

详细信息

作者简介:
伍冬睿：华中科技大学人工智能与自动化学院教授. 主要研究方向为机器学习, 脑机接口, 计算智能, 情感计算. 本文通信作者.E-mail: drwu@hust.edu.cn

曾志刚：华中科技大学人工智能与自动化学院院长, 教授. 主要研究方向为神经网络理论与应用, 动力系统稳定性, 联想记忆.E-mail: zgzeng@mail.hust.edu.cn

莫红：长沙理工大学电气与信息工程学院教授. 2004年获中国科学院自动化研究所工学博士学位. 主要研究方向为模糊AI, 智慧医疗, 复杂系统的管理与控制. E-mail: mohong198@163.com

王飞跃：中国科学院自动化研究所复杂系统管理与控制国家重点实验室主任, 国防科技大学军事计算实验与平行系统技术研究中心主任, 中国科学院大学中国经济与社会安全研究中心主任, 青岛智能产业技术研究院院长. 主要研究方向为平行系统的方法与应用, 社会计算, 平行智能以及知识自动化. E-mail: feiyue.wang@ia.ac.cn

计量
- 文章访问数: 2942
- HTML全文浏览量: 828
- PDF下载量: 993
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-16
- 录用日期: 2020-05-12
- 网络出版日期: 2020-08-26
- 刊出日期: 2020-08-26

Interval Type-2 Fuzzy Sets and Systems: Overview and Outlook

1.
Ministry of Education Key Laboratory on Image Information Processing and Intelligent Control, School of Artificial Intelligence and Automation, Huazhong University of Science and Technology, Wuhan 430074
2.
School of Electric and Information Engineering, Changsha University of Science and Technology, Changsha 410114
3.
The State Key Laboratory for Management and Control of Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190

Funds: Supported by National Natural Science Foundation of China (61873321, U1913207), Technology Innovation Project of Hubei Province of China (2019AEA171), NSFC-Shenzhen Robotics Basic Research Center (U1913207), and International Science and Technology Cooperation Program of China (2017YFE0128300)

摘要

摘要: 一型模糊集可以建模单个用户的语义概念中的不确定性, 即个体内不确定性. 一型模糊系统在控制和机器学习中得到了大量成功应用. 区间二型模糊集能同时建模个体内不确定性和个体间不确定性, 因而在很多应用中显示了比一型模糊系统更好的性能, 是近年来的研究热点. 本文首先介绍了区间二型模糊集的重要概念和理论研究进展, 总结了其在决策和机器学习中的成功应用, 然后介绍了区间二型模糊系统的基本操作和理论研究进展, 并回顾了其在控制和机器学习中的典型应用. 最后, 对区间二型模糊集和模糊系统未来的研究方向进行了展望.
- 区间二型模糊集 /
- 区间二型模糊系统 /
- 模糊控制 /
- 感知计算
Abstract: Type-1 fuzzy sets can model the linguistic uncertainty from a single user, i.e., intra-personal uncertainty. Type-1 fuzzy systems have been widely used in controls and machine learning applications. Interval type-2 fuzzy sets can simultaneously model both intra-personal uncertainty and inter-personal uncertainty, and hence have demonstrated better performance than type-1 fuzzy systems in many applications, becoming a hot research topic recently. This paper first introduces main concepts and theoretical research progresses of interval type-2 fuzzy sets, summarizes their successful applications in decision-making and machine learning, then introduces basic operations and theoretical research progresses of interval type-2 fuzzy systems, and reviews their typical applications in controls and machine learning. Finally, it points out several future research directions on interval type-2 fuzzy sets and systems.
- Interval type-2 fuzzy set /
- interval type-2 fuzzy system /
- fuzzy control /
- perceptual computing

HTML全文

图 1 “高温”的不同集合表示

Fig. 1 Different representations of “High temperature”

下载: 全尺寸图片幻灯片

图 2 谷歌学术中包含“type-2 fuzzy”的论文数量

Fig. 2 Number of publications on “type-2 fuzzy” in Google Scholar

下载: 全尺寸图片幻灯片

图 3 二型模糊集

Fig. 3 Type-2 fuzzy sets

下载: 全尺寸图片幻灯片

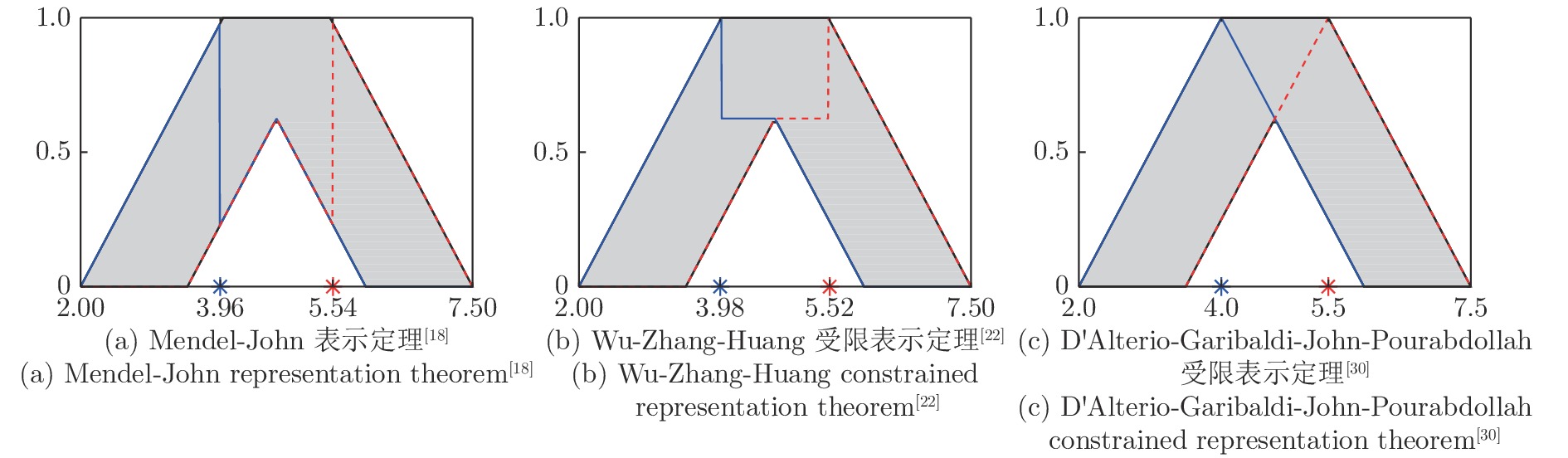
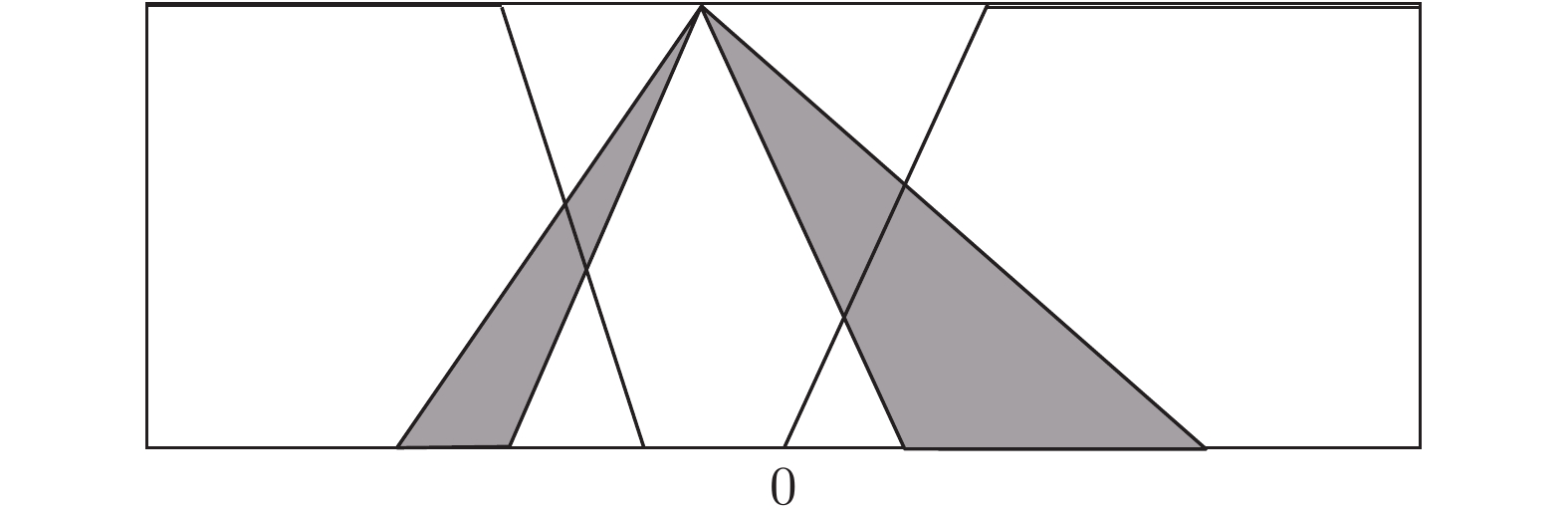
图 4 根据不同的表示定理, 计算区间二型模糊集质心所用到的嵌入一型模糊集(左边的点是由实线嵌入一型模糊集决定的质心的下界, 右边的点是由虚线嵌入一型模糊集决定的质心的上界.)

Fig. 4 Embedded type-1 fuzzy sets in computing the centroid of the interval type-2 fuzzy set, according to different representation theorems (The left dot is the lower bound of the centroid determined by the solid embedded type-1 fuzzy set, and the right dot is the upper bound determined by the dashed embedded type-1 fuzzy set.)

下载: 全尺寸图片幻灯片

图 5 各种不同的加权平均

Fig. 5 Various weighted averages

下载: 全尺寸图片幻灯片

图 6 感知计算机

Fig. 6 Perceptual computer

下载: 全尺寸图片幻灯片

图 7 区间二型模糊系统

Fig. 7 Interval type-2 fuzzy system

下载: 全尺寸图片幻灯片

图 8 转换点

Fig. 8 The switch points

下载: 全尺寸图片幻灯片

图 9 简化的区间二型模糊系统输入域中使用的模糊集示例

Fig. 9 MFs in a simplified interval type-2 fuzzy system

下载: 全尺寸图片幻灯片

图 10 区间二型模糊系统的不连续性

Fig. 10 Discontinuity of interval type-2 fuzzy systems

下载: 全尺寸图片幻灯片

图 11 区间二型模糊控制器的隶属度函数

Fig. 11 MFs of the interval type-2 fuzzy controller

下载: 全尺寸图片幻灯片

图 12 式$(25)\sim (27) $决定的输入区域

Fig. 12 Input region determined by $(25)\sim (27) $

下载: 全尺寸图片幻灯片

图 13 $\alpha$, $\beta$和$\dot{e}$的关系

Fig. 13 Relationship between $\alpha$, $\beta$ and $\dot{e}$

下载: 全尺寸图片幻灯片

图 14 对于区间二型模糊系统初学者的建议

Fig. 14 Recommendations on designing interval type-2 fuzzy system for beginners

下载: 全尺寸图片幻灯片

参考文献(151)

[1]	Zadeh L A. Fuzzy sets. Information and Control, 1965, 8(3): 338−353 doi: 10.1016/S0019-9958(65)90241-X
[2]	Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning-I. Information Sciences, 1975, 8(3): 199−249 doi: 10.1016/0020-0255(75)90036-5
[3]	Turksen I B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets and Systems, 1986, 20(2): 191−210 doi: 10.1016/0165-0114(86)90077-1
[4]	Gorzałczany M B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets and Systems, 1987, 21(1): 1−17 doi: 10.1016/0165-0114(87)90148-5
[5]	Bustince H. Indicator of inclusion grade for interval-valued fuzzy sets. International Journal of Approximate Reasoning, 2000, 23(3): 137−209 doi: 10.1016/S0888-613X(99)00045-6
[6]	Atanassov K T. Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 1986, 20(1): 87−96 doi: 10.1016/S0165-0114(86)80034-3
[7]	Deschrijver G, Kerre E E. On the relationship between some extensions of fuzzy set theory. Fuzzy Sets and Systems, 2003, 133(2): 227−235 doi: 10.1016/S0165-0114(02)00127-6
[8]	Sola H B, Fernandez J, Hagras H, Herrera F, Pagola M, Barrenechea E. Interval type-2 fuzzy sets are generalization of interval-valued fuzzy sets: Toward a wider view on their relationship. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1876−1882 doi: 10.1109/TFUZZ.2014.2362149
[9]	Mendel J M, Hagras H, Bustince H, Herrera F. Comments on “Interval type-2 fuzzy sets are generalization of interval-valued fuzzy sets: Towards a wide view on their relationship”. IEEE Transactions on Fuzzy Systems, 2016, 24(1): 249−250 doi: 10.1109/TFUZZ.2015.2446508
[10]	Mendel J M. Uncertain Rule-Based Fuzzy Systems: Introduction and New Directions (Second Edition). Berlin: Springer, 2017.
[11]	Zadeh L A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transactions on Systems, Man, and Cybernetics, 1973, SMC-3(1): 28−44 doi: 10.1109/TSMC.1973.5408575
[12]	Mamdani E H. Application of fuzzy algorithms for control of simple dynamic plant. Proceedings of the Institution of Electrical Engineers, 1974, 121(12): 1585−1588 doi: 10.1049/piee.1974.0328
[13]	Holmblad L P, Ostergaard J J. Control of a cement kiln by fuzzy logic techniques. IFAC Proceedings, 1981, 14(2): 809−814 doi: 10.1016/S1474-6670(17)63582-1
[14]	潘永平, 黄道平, 孙宗海. II型模糊控制综述. 控制理论与应用, 2011, 28(1): 13−23 Pan Yong-Ping, Huang Dao-Ping, Sun Zong-Hai. Overview of type-2 fuzzy logic control. Control Theory & Applications, 2011, 28(1): 13−23
[15]	Mendel J M. Fuzzy logic systems for engineering: A tutorial. Proceedings of the IEEE, 1995, 83(3): 345−377 doi: 10.1109/5.364485
[16]	Wang L X. A Course in Fuzzy Systems and Control. Upper Saddle River, NJ: Prentice Hall, 1997.
[17]	王飞跃, 莫红. 关于二型模糊集合的一些基本问题. 自动化学报, 2017, 43(7): 1114−1141 Wang Fei-Yue, Mo Hong. Some fundamental issues on type-2 fuzzy sets. Acta Automatica Sinica, 2017, 43(7): 1114−1141
[18]	Mendel J M, John R I B. Type-2 fuzzy sets made simple. IEEE Transactions on Fuzzy Systems, 2002, 10(2): 117−127 doi: 10.1109/91.995115
[19]	Wu D R, Mendel J M. Uncertainty measures for interval type-2 fuzzy sets. Information Sciences, 2007, 177(23): 5378−5393 doi: 10.1016/j.ins.2007.07.012
[20]	Wu D R, Mendel J M. A comparative study of ranking methods, similarity measures and uncertainty measures for interval type-2 fuzzy sets. Information Sciences, 2009, 179(8): 1169−1192 doi: 10.1016/j.ins.2008.12.010
[21]	Mendel J M, Wu D R. Perceptual Computing: Aiding People in Making Subjective Judgments. Hoboken, NJ: Wiley-IEEE Press, 2010.
[22]	Wu D R, Zhang H T, Huang J. A constrained representation theorem for well-shaped interval type-2 fuzzy sets, and the corresponding constrained uncertainty measures. IEEE Transactions on Fuzzy Systems, 2019, 27(6): 1237−1251 doi: 10.1109/TFUZZ.2018.2874018
[23]	Liu F L, Mendel J M. Encoding words into interval type-2 fuzzy sets using an interval approach. IEEE Transactions on Fuzzy Systems, 2008, 16(6): 1503−1521 doi: 10.1109/TFUZZ.2008.2005002
[24]	Wu D R, Mendel J M, Coupland S. Enhanced interval approach for encoding words into interval type-2 fuzzy sets and its convergence analysis. IEEE Transactions on Fuzzy Systems, 2012, 20(3): 499−513 doi: 10.1109/TFUZZ.2011.2177272
[25]	Hao M S, Mendel J M. Encoding words into normal interval type-2 fuzzy sets: HM approach. IEEE Transactions on Fuzzy Systems, 2016, 24(4): 865−879 doi: 10.1109/TFUZZ.2015.2486814
[26]	Wu D R, Mendel J M. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1145−1161 doi: 10.1109/TFUZZ.2007.896325
[27]	Wu D R, Mendel J M. Ordered fuzzy weighted averages and ordered linguistic weighted averages. In: Proceedings of the 2010 IEEE International Conference on Fuzzy Systems. Barcelona, Spain: IEEE, 2010.
[28]	Wu D R, Mendel J M. Perceptual reasoning for perceptual computing: A similarity-based approach. IEEE Transactions on Fuzzy Systems, 2009, 17(6): 1397−1411 doi: 10.1109/TFUZZ.2009.2032652
[29]	Mendel J M, Wu D R. Perceptual reasoning for perceptual computing. IEEE Transactions on Fuzzy Systems, 2008, 16(6): 1550−1564 doi: 10.1109/TFUZZ.2008.2005691
[30]	D'Alterio P, Garibaldi J M, John R, Pourabdollah A. Constrained interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 2020, DOI: 10.1109/TFUZZ.2020.2970911
[31]	Huang J, Ri M, Wu D R, Ri S. Interval type-2 fuzzy logic modeling and control of a mobile two-wheeled inverted pendulum. IEEE Transactions on Fuzzy Systems, 2018, 26(4): 2030−2038 doi: 10.1109/TFUZZ.2017.2760283
[32]	Wu D, Tan W W. A type-2 fuzzy logic controller for the liquid-level process. In: Proceedings of the 2004 IEEE International Conference on Fuzzy Systems. Budapest, Hungary: IEEE, 2004. 953−958
[33]	Tahayori H, Livi L, Sadeghian A, Rizzi A. Interval type-2 fuzzy set reconstruction based on fuzzy information-theoretic kernels. IEEE Transactions on Fuzzy Systems, 2015, 23(4): 1014−1029 doi: 10.1109/TFUZZ.2014.2336673
[34]	Wu D R, Tan W W. A simplified type-2 fuzzy logic controller for real-time control. ISA Transactions, 2006, 45(4): 503−516 doi: 10.1016/S0019-0578(07)60228-6
[35]	Zadeh L A. Toward a generalized theory of uncertainty (GTU) — An outline. Information Sciences, 2005, 172(1-2): 1−40 doi: 10.1016/j.ins.2005.01.017
[36]	Klir G J. Principles of uncertainty: What are they? Why do we need them? Fuzzy Sets and Systems, 1995, 74(1): 15−31
[37]	Christensen R. Entropy minimax multivariate statistical modeling-I: Theory. International Journal of General Systems, 1985, 11(3): 231−277 doi: 10.1080/03081078508934916
[38]	Christensen R. Entropy minimax multivariate statistical modeling-II: Applications. International Journal of General Systems, 1986, 12(3): 227−305 doi: 10.1080/03081078608934938
[39]	Paris J B. The Uncertain Reasoner's Companion-A Mathematical Perspective. Cambridge: Cambridge University Press, 1994.
[40]	Geer J F, Klir G J. A mathematical analysis of information-preserving transformations between probabilistic and possibilistic formulations of uncertainty. International Journal of General Systems, 1992, 20(2): 143−176 doi: 10.1080/03081079208945024
[41]	Klir G J. A principle of uncertainty and information invariance. International Journal of General Systems, 1990, 17(2-3): 249−275 doi: 10.1080/03081079008935110
[42]	Klir G J, Parviz B. Probability-possibility transformations: A comparison. International Journal of General Systems, 1992, 21(3): 291−310 doi: 10.1080/03081079208945083
[43]	Wonneberge S. Generalization of an invertible mapping between probability and possibility. Fuzzy Sets and Systems, 1994, 64(2): 229−240 doi: 10.1016/0165-0114(94)90336-0
[44]	Liu F L, Mendel J M. Aggregation using the fuzzy weighted average as computed by the Karnik-Mendel algorithms. IEEE Transactions on Fuzzy Systems, 2008, 16(1): 1−12 doi: 10.1109/TFUZZ.2007.896229
[45]	Wu D R, Mendel J M. Corrections to “Aggregation using the linguistic weighted average and interval type-2 fuzzy sets”. IEEE Transactions on Fuzzy Systems, 2008, 16(6): 1664−1666 doi: 10.1109/TFUZZ.2008.2005941
[46]	Klir G J, Yuan B. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Upper Saddle River, NJ: Prentice-Hall, 1995
[47]	Karnik N N, Mendel J M, Liang Q L. Type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 1999, 7(6): 643−658 doi: 10.1109/91.811231
[48]	Wu D R, Huang J. Ordered novel weighted averages. Type-2 Fuzzy Logic and Systems. Berlin: Springer, 2018. 25-47
[49]	Yager R R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Transactions on Systems, Man, and Cybernetics, 1988, 18(1): 183−190 doi: 10.1109/21.87068
[50]	Mendel J M. Computing with words: Zadeh, Turing, Popper and Occam. IEEE Computational Intelligence Magazine, 2007, 2(4): 10−17 doi: 10.1109/MCI.2007.9066897
[51]	Mendel J M. Type-2 fuzzy sets as well as computing with words. IEEE Computational Intelligence Magazine, 2019, 14(1): 82−95 doi: 10.1109/MCI.2018.2881646
[52]	Mendel J M. The perceptual computer: An architecture for computing with words. In: Proceedings of the 10th IEEE International Conference on Fuzzy Systems. Melbourne, Australia: IEEE, 2001. 35−38
[53]	Acosta H, Wu D R, Forrest B M. Fuzzy experts on recreational vessels, a risk modelling approach for marine invasions. Ecological Modelling, 2010, 221(5): 850−863 doi: 10.1016/j.ecolmodel.2009.11.025
[54]	Wu D R, Mendel J M. Computing with words for hierarchical decision making applied to evaluating a weapon system. IEEE Transactions on Fuzzy Systems, 2010, 18(3): 441−460 doi: 10.1109/TFUZZ.2010.2043439
[55]	Chen S M, Hong J A. Fuzzy multiple attributes group decision-making based on ranking interval type-2 fuzzy sets and the TOPSIS method. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2014, 44(12): 1665−1673 doi: 10.1109/TSMC.2014.2314724
[56]	Qin J D, Liu X W, Pedrycz W. An extended VIKOR method based on prospect theory for multiple attribute decision making under interval type-2 fuzzy environment. Knowledge-Based Systems, 2015, 86: 116−130 doi: 10.1016/j.knosys.2015.05.025
[57]	Qin J D, Liu X W, Pedrycz W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. European Journal of Operational Research, 2017, 258(2): 626−638 doi: 10.1016/j.ejor.2016.09.059
[58]	李润梅, 梁秋鸿. 基于区间二型模糊集合的人工交通系统可信度评估. 自动化学报, 2019, 45(10): 1915−1922 Li Run-Mei, Liang Qiu-Hong. Artificial traffic system credibility evaluation with interval type-2 fuzzy sets. Acta Automatica Sinica, 2019, 45(10): 1915−1922
[59]	Yager R R. A new approach to the summarization of data. Information Sciences, 1982, 28(1): 69−86 doi: 10.1016/0020-0255(82)90033-0
[60]	Wu D R, Mendel J M. Linguistic summarization using IF-THEN rules and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 2011, 19(1): 136−151 doi: 10.1109/TFUZZ.2010.2088128
[61]	Boran F E, Akay D. A generic method for the evaluation of interval type-2 fuzzy linguistic summaries. IEEE Transactions on Cybernetics, 2014, 44(9): 1632−1645 doi: 10.1109/TCYB.2013.2291272
[62]	Karnik N N, Mendel J M. Centroid of a type-2 fuzzy set. Information Sciences, 2001, 132(1-4): 195−220 doi: 10.1016/S0020-0255(01)00069-X
[63]	Sumati V, Patvardhan C. Interval type-2 mutual subsethood fuzzy neural inference system (IT2MSFuNIS). IEEE Transactions on Fuzzy Systems, 2018, 26(1): 203−215 doi: 10.1109/TFUZZ.2016.2646750
[64]	Wu D R. Approaches for reducing the computational cost of interval type-2 fuzzy logic systems: Overview and comparisons. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 80−99 doi: 10.1109/TFUZZ.2012.2201728
[65]	Wu D R, Mendel J M. Enhanced Karnik-Mendel algorithms. IEEE Transactions on Fuzzy Systems, 2009, 17(4): 923−934 doi: 10.1109/TFUZZ.2008.924329
[66]	Wu D R, Nie M W. Comparison and practical implementation of type-reduction algorithms for type-2 fuzzy sets and systems. In: Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011). Taipei, China: IEEE, 2011. 2131−2138
[67]	Wu D R, Tan W W. Computationally efficient type-reduction strategies for a type-2 fuzzy logic controller. In: Proceedings of the 14th IEEE International Conference on Fuzzy Systems. Reno, USA: IEEE, 2005. 353−358
[68]	Begian M B, Melek W W, Mendel J M. Stability analysis of type-2 fuzzy systems. In: Proceedings of the 2008 IEEE International Conference on Fuzzy Systems. Hong Kong, China: IEEE, 2008. 947−953
[69]	Nie M W, Tan W W. Towards an efficient type-reduction method for interval type-2 fuzzy logic systems. In: Proceedings of the 2008 IEEE International Conference on Fuzzy Systems. Hong Kong, China: IEEE, 2008. 1425−1432
[70]	Wu D R, Tan W W. Genetic learning and performance evaluation of interval type-2 fuzzy logic controllers. Engineering Applications of Artificial Intelligence, 2006, 19(8): 829−841 doi: 10.1016/j.engappai.2005.12.011
[71]	Wu D, Tan X. Multitasking genetic algorithm (MTGA) for fuzzy system optimization. IEEE Transactions on Fuzzy System, 2020, 28(6): 1050−1061
[72]	Das A K, Subramanian K, Sundaram S. An evolving interval type-2 neurofuzzy inference system and its metacognitive sequential learning algorithm. IEEE Transactions on Fuzzy Systems, 2015, 23(6): 2080−2093 doi: 10.1109/TFUZZ.2015.2403793
[73]	Lin Y Y, Liao S H, Chang J Y, Lin C T. Simplified interval type-2 fuzzy neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(5): 959−969 doi: 10.1109/TNNLS.2013.2284603
[74]	Juang C F, Tsao Y W. A self-evolving interval type-2 fuzzy neural network with online structure and parameter learning. IEEE Transactions on Fuzzy Systems, 2008, 16(6): 1411−1424 doi: 10.1109/TFUZZ.2008.925907
[75]	Juang C F, Huang R B, Lin Y Y. A recurrent self-evolving interval type-2 fuzzy neural network for dynamic system processing. IEEE Transactions on Fuzzy Systems, 2009, 17(5): 1092−1105 doi: 10.1109/TFUZZ.2009.2021953
[76]	Deng Z H, Choi K S, Cao L B, Wang S T. T2FELA: Type-2 fuzzy extreme learning algorithm for fast training of interval type-2 TSK fuzzy logic system. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 664−676 doi: 10.1109/TNNLS.2013.2280171
[77]	Wu D R, Mendel J M. On the continuity of type-1 and interval type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 2011, 19(1): 179−192 doi: 10.1109/TFUZZ.2010.2091962
[78]	Lam H K, Seneviratne L D. Stability analysis of interval type-2 fuzzy-model-based control systems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2008, 38(3): 617−628 doi: 10.1109/TSMCB.2008.915530
[79]	Biglarbegian M, Melek W W, Mendel J M. On the stability of interval type-2 TSK fuzzy logic control systems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2010, 40(3): 798−818 doi: 10.1109/TSMCB.2009.2029986
[80]	Jafarzadeh S, Fadali M S, Sonbol A H. Stability analysis and control of discrete type-1 and type-2 TSK fuzzy systems: Part I. Stability analysis. IEEE Transactions on Fuzzy Systems, 2011, 19(6): 989−1000 doi: 10.1109/TFUZZ.2011.2158218
[81]	Kumbasar T. Robust stability analysis and systematic design of single-input interval type-2 fuzzy logic controllers. IEEE Transactions on Fuzzy Systems, 2016, 24(3): 675−694 doi: 10.1109/TFUZZ.2015.2471805
[82]	Xiao B, Lam H K, Li H Y. Stabilization of interval type-2 polynomial-fuzzy-model-based control systems. IEEE Transactions on Fuzzy Systems, 2017, 25(1): 205−217 doi: 10.1109/TFUZZ.2016.2554153
[83]	Rong N N, Wang Z S, Zhang H G. Finite-time stabilization for discontinuous interconnected delayed systems via interval type-2 T-S fuzzy model approach. IEEE Transactions on Fuzzy Systems, 2019, 27(2): 249−261 doi: 10.1109/TFUZZ.2018.2856181
[84]	Li C D, Yi J Q, Wang M, Zhang G Q. Monotonic type-2 fuzzy neural network and its application to thermal comfort prediction. Neural Computing and Applications, 2013, 23(7-8): 1987−1998 doi: 10.1007/s00521-012-1140-x
[85]	Li C D, Yi J Q, Zhang G Q. On the monotonicity of interval type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 2014, 22(5): 1197−1212 doi: 10.1109/TFUZZ.2013.2286416
[86]	Wang T C, Tong S C, Yi J Q, Li H Y. Adaptive inverse control of cable-driven parallel system based on type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1803−1816 doi: 10.1109/TFUZZ.2014.2379284
[87]	Wu D R. Design and Analysis of Type-2 Fuzzy Logic Systems [Master thesis], National University of Singapore, Singapore, 2006
[88]	Wu D R, Tan W W. Interval type-2 fuzzy PI controllers: Why they are more robust. In: Proceedings of the 2010 IEEE International Conference on Granular Computing. San Jose, USA: IEEE, 2010. 802−807
[89]	Wu D R. On the fundamental differences between interval type-2 and type-1 fuzzy logic controllers. IEEE Transactions on Fuzzy Systems, 2012, 20(5): 832−848 doi: 10.1109/TFUZZ.2012.2186818
[90]	Du X Y, Ying H. Derivation and analysis of the analytical structures of the interval type-2 fuzzy-PI and PD controllers. IEEE Transactions on Fuzzy Systems, 2010, 18(4): 802−814 doi: 10.1109/TFUZZ.2010.2049022
[91]	Nie M W, Tan W W. Analytical structure and characteristics of symmetric Karnik-Mendel type-reduced interval type-2 fuzzy PI and PD controllers. IEEE Transactions on Fuzzy Systems, 2012, 20(3): 416−430 doi: 10.1109/TFUZZ.2011.2174061
[92]	Zhou H B, Ying H. A method for deriving the analytical structure of a broad class of typical interval type-2 Mamdani fuzzy controllers. IEEE Transactions on Fuzzy Systems, 2013, 21(3): 447−458 doi: 10.1109/TFUZZ.2012.2226891
[93]	Zhou H B, Ying H. Deriving and analyzing analytical structures of a class of typical interval type-2 TS fuzzy controllers. IEEE Transactions on Cybernetics, 2017, 47(9): 2492−2503 doi: 10.1109/TCYB.2016.2570239
[94]	Zhou H B, Ying H, Zhang C L. Effects of increasing the footprints of uncertainty on analytical structure of the classes of interval type-2 mamdani and TS fuzzy controllers. IEEE Transactions on Fuzzy Systems, 2019, 27(9): 1881−1890 doi: 10.1109/TFUZZ.2019.2892354
[95]	Wu D R, Tan W W. Type-2 FLS modeling capability analysis. In: Proceedings of the 14th IEEE International Conference on Fuzzy Systems. Reno, USA: IEEE, 2005. 242−247
[96]	Wu D R, Mendel J M. Recommendations on designing practical interval type-2 fuzzy systems. Engineering Applications of Artificial Intelligence, 2019, 85: 182−193 doi: 10.1016/j.engappai.2019.06.012
[97]	Hagras H. Type-2 FLCs: A new generation of fuzzy controllers. IEEE Computational Intelligence Magazine, 2007, 2(1): 30−43 doi: 10.1109/MCI.2007.357192
[98]	Hagras H A. A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots. IEEE Transactions on Fuzzy Systems, 2004, 12(4): 524−539 doi: 10.1109/TFUZZ.2004.832538
[99]	Liu Z, Zhang Y, Wang Y N. A type-2 fuzzy switching control system for biped robots. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(6): 1202−1213 doi: 10.1109/TSMCC.2007.900649
[100]	Chaoui H, Gueaieb W. Type-2 fuzzy logic control of a flexible-joint manipulator. Journal of Intelligent and Robotic Systems, 2008, 51(2): 159−186 doi: 10.1007/s10846-007-9185-2
[101]	Lin F J, Chou P H. Adaptive control of two-axis motion control system using interval type-2 fuzzy neural network. IEEE Transactions on Industrial Electronics, 2009, 56(1): 178−193 doi: 10.1109/TIE.2008.927225
[102]	Martínez R, Castillo O, Aguilar L T. Optimization of interval type-2 fuzzy logic controllers for a perturbed autonomous wheeled mobile robot using genetic algorithms. Information Sciences, 2009, 179(13): 2158−2174 doi: 10.1016/j.ins.2008.12.028
[103]	Lin T C, Liu H L, Kuo M J. Direct adaptive interval type-2 fuzzy control of multivariable nonlinear systems. Engineering Applications of Artificial Intelligence, 2009, 22(3): 420−430 doi: 10.1016/j.engappai.2008.10.024
[104]	李成栋, 易建强, 余意, 赵冬斌. 柔索驱动并联机构的二型模糊神经逆控制. 自动化学报, 2010, 36(3): 459−464 Li Cheng-Dong, Yi Jian-Qiang, Yu Yi, Zhao Dong-Bin. Inverse control of cable-driven parallel mechanism using type-2 fuzzy neural network. Acta Automatica Sinica, 2010, 36(3): 459−464
[105]	Abiyev R H, Kaynak O. Type 2 fuzzy neural structure for identification and control of time-varying plants. IEEE Transactions on Industrial Electronics, 2010, 57(12): 4147−4159 doi: 10.1109/TIE.2010.2043036
[106]	Biglarbegian M, Melek W W, Mendel J M. Design of novel interval type-2 fuzzy controllers for modular and reconfigurable robots: Theory and experiments. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1371−1384 doi: 10.1109/TIE.2010.2049718
[107]	Lam H K, Li H Y, Deters C, Secco E L, Wurdemann H, Althoefer K. Control design for interval type-2 fuzzy systems under imperfect premise matching. IEEE Transactions on Industrial Electronics, 2014, 61(2): 956−968 doi: 10.1109/TIE.2013.2253064
[108]	Taghavifar H, Xu B, Hu C, Qin Y , Wei C. Commercial vehicle-based robust control of seated whole-body vibration using adaptive indirect type-2 fuzzy neural network. IEEE Access, 2020, 8: 124949−124960
[109]	Li Y M, Sun Y Y, Hua J, Li L. Indirect adaptive type-2 fuzzy impulsive control of nonlinear systems. IEEE Transactions on Fuzzy Systems, 2015, 23(4): 1084−1099 doi: 10.1109/TFUZZ.2014.2346235
[110]	Raju S K, Pillai G N. Design and implementation of type-2 fuzzy logic controller for DFIG-based wind energy systems in distribution networks. IEEE Transactions on Sustainable Energy, 2016, 7(1): 345−353 doi: 10.1109/TSTE.2015.2496170
[111]	Navarro G, Umberger D K, Manic M. VD-IT2, virtual disk cloning on disk arrays using a type-2 fuzzy controller. IEEE Transactions on Fuzzy Systems, 2017, 25(6): 1752−1764 doi: 10.1109/TFUZZ.2016.2633371
[112]	Ren G P, Chen Z Y, Zhang H T, Wu Y, Meng H F, Wu D R, et al. Design of interval type-2 fuzzy controllers for active magnetic bearing systems. IEEE/ASME Transactions on Mechatronics, 2020, DOI: 10.1109/TMECH.2020.2978018
[113]	Wei Z X, Doctor F, Liu Y X, Fan S Z, Shieh J S. An optimized type-2 self-organizing fuzzy logic controller applied in anesthesia for propofol dosing to regulate BIS. IEEE Transactions on Fuzzy Systems, 2020, 28(6): 1062−1072 doi: 10.1109/TFUZZ.2020.2969384
[114]	Liang Q, Karnik N N, Mendel J M. Connection admission control in ATM networks using survey-based type-2 fuzzy logic systems. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2000, 30(3): 329−339 doi: 10.1109/5326.885114
[115]	Li H Y, Wu C W, Shi P, Gao Y B. Control of nonlinear networked systems with packet dropouts: Interval type-2 fuzzy model-based approach. IEEE Transactions on Cybernetics, 2015, 45(11): 2378−2389 doi: 10.1109/TCYB.2014.2371814
[116]	Zhao T, Dian S Y. State feedback control for interval type-2 fuzzy systems with time-varying delay and unreliable communication links. IEEE Transactions on Fuzzy Systems, 2018, 26(2): 951−966 doi: 10.1109/TFUZZ.2017.2699947
[117]	Tang X M, Deng L, Yu J M, Qu H C. Output feedback predictive control of interval type-2 T-S fuzzy systems with Markovian packet loss. IEEE Transactions on Fuzzy Systems, 2018, 26(4): 2450−2459 doi: 10.1109/TFUZZ.2017.2771502
[118]	Khooban M H, Gheisarnejad M. A novel deep reinforcement learning controller based type-II fuzzy system: frequency regulation in microgrids. IEEE Transactions on Emerging Topics in Computational Intelligence, 2020, DOI: 10.1109/TETCI.2020.2964886
[119]	Hu Z J, Liu S C, Yang L, Wu L G. Distributed fuzzy filtering for load frequency control of non-linear interconnected power systems under cyber-physical attacks. IET Control Theory & Applications, 2020, 14(4): 527−538
[120]	Li X H, Ye D. Asynchronous event-triggered control for networked interval type-2 fuzzy systems against dos attacks. IEEE Transactions on Fuzzy Systems, 2020, DOI: 10.1109/TFUZZ.2020.2975495
[121]	Zhang Z N, Niu Y G, Cao Z R, Song J. Security sliding mode control of interval type-2 fuzzy systems subject to cyber attacks: the stochastic communication protocol case. IEEE Transactions on Fuzzy Systems, 2020, DOI: 10.1109/TFUZZ.2020.2972785
[122]	Das A K, Sundaram S, Sundararajan N. A self-regulated interval type-2 neuro-fuzzy inference system for handling nonstationarities in EEG signals for BCI. IEEE Transactions on Fuzzy Systems, 2016, 24(6): 1565−1577 doi: 10.1109/TFUZZ.2016.2540072
[123]	Herman P A, Prasad G, McGinnity T M. Designing an interval type-2 fuzzy logic system for handling uncertainty effects in brain-computer interface classification of motor imagery induced EEG patterns. IEEE Transactions on Fuzzy Systems, 2017, 25(1): 29−42 doi: 10.1109/TFUZZ.2016.2637934
[124]	Singh V, Dev R, Dhar N K, Agrawal P, Verma N K. Adaptive type-2 fuzzy approach for filtering salt and pepper noise in grayscale images. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 3170−3176 doi: 10.1109/TFUZZ.2018.2805289
[125]	Wu H Y, Wu Y Y, Luo J P. An interval type-2 fuzzy rough set model for attribute reduction. IEEE Transactions on Fuzzy Systems, 2009, 17(2): 301−315 doi: 10.1109/TFUZZ.2009.2013458
[126]	Maji P, Garai P. IT2 fuzzy-rough sets and max relevance-max significance criterion for attribute selection. IEEE Transactions on Cybernetics, 2015, 45(8): 1657−1668 doi: 10.1109/TCYB.2014.2357892
[127]	Lin C T, Pal N R, Wu S L, Liu Y T, Lin Y Y. An interval type-2 neural fuzzy system for online system identification and feature elimination. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(7): 1442−1455 doi: 10.1109/TNNLS.2014.2346537
[128]	Chakraborty B, Ghosh L, Konar A. Optimal selection of EEG electrodes using interval type-2 fuzzy-logic-based semiseparating signaling game. IEEE Transactions on Cybernetics, 2020, DOI: 10.1109/TCYB.2020.2968625
[129]	Hwang C, Rhee F C H. Uncertain fuzzy clustering: Interval type-2 fuzzy approach to C-means. IEEE Transactions on Fuzzy Systems, 2007, 15(1): 107−120 doi: 10.1109/TFUZZ.2006.889763
[130]	Zhao F, Chen Y L, Liu H Q, Fan J L. Alternate PSO-based adaptive interval type-2 intuitionistic fuzzy C-means clustering algorithm for color image segmentation. IEEE Access, 2019, 7: 64028−64039 doi: 10.1109/ACCESS.2019.2916894
[131]	Zeng J, Liu Z Q. Type-2 fuzzy hidden Markov models and their application to speech recognition. IEEE Transactions on Fuzzy Systems, 2006, 14(3): 454−467 doi: 10.1109/TFUZZ.2006.876366
[132]	Subramanian K, Savitha R, Suresh S. A metacognitive complex-valued interval type-2 fuzzy inference system. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(9): 1659−1672 doi: 10.1109/TNNLS.2014.2321420
[133]	Cao X Q, Liu Z Q. Type-2 fuzzy topic models for human action recognition. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1581−1593 doi: 10.1109/TFUZZ.2014.2370678
[134]	Juang C F, Wang P H. An interval type-2 neural fuzzy classifier learned through soft margin minimization and its human posture classification application. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1474−1487 doi: 10.1109/TFUZZ.2014.2362547
[135]	Rubio-Solis A, Panoutsos G. Interval type-2 radial basis function neural network: a modeling framework. IEEE Transactions on Fuzzy Systems, 2015, 23(2): 457−473 doi: 10.1109/TFUZZ.2014.2315656
[136]	Mo H, Wang J, Li X, Wu Z L. Linguistic dynamic modeling and analysis of psychological health state using interval type-2 fuzzy sets. IEEE/CAA Journal of Automatica Sinica, 2015, 2(4): 366−373 doi: 10.1109/JAS.2015.7296531
[137]	Kim E H, Oh S K, Pedrycz W. Design of reinforced interval type-2 fuzzy C-means-based fuzzy classifier. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 3054−3068 doi: 10.1109/TFUZZ.2017.2785244
[138]	Eyoh I, John R, De Maere G, Kayacan E. Hybrid learning for interval type-2 intuitionistic fuzzy logic systems as applied to identification and prediction problems. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 2672−2685 doi: 10.1109/TFUZZ.2018.2803751
[139]	Cao B, Zhao J W, Lv Z H, Gu Y, Yang P, Halgamuge S. Multiobjective evolution of fuzzy rough neural network via distributed parallelism for stock prediction. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 939−952 doi: 10.1109/TFUZZ.2020.2972207
[140]	Han M, Zhong K, Qiu T, Han B. Interval type-2 fuzzy neural networks for chaotic time series prediction: A concise overview. IEEE Transactions on Cybernetics, 2019, 49(7): 2720−2731 doi: 10.1109/TCYB.2018.2834356
[141]	Pratama M, Lu J, Zhang G Q. Evolving type-2 fuzzy classifier. IEEE Transactions on Fuzzy Systems, 2016, 24(3): 574−589 doi: 10.1109/TFUZZ.2015.2463732
[142]	Aisbett J, Rickard J T, Morgenthaler D G. Type-2 fuzzy sets as functions on spaces. IEEE Transactions on Fuzzy Systems, 2010, 18(4): 841−844 doi: 10.1109/TFUZZ.2010.2046176
[143]	Mendel J M, Rajati M R, Sussner P. On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Information Sciences, 2016, 340-341: 337−345 doi: 10.1016/j.ins.2016.01.015
[144]	Wu D R, Lin C T, Huang J, Zeng Z G. On the functional equivalence of TSK fuzzy systems to neural networks, mixture of experts, CART, and stacking ensemble regression. IEEE Transactions on Fuzzy Systems, 2020, DOI: 10.1109/TFUZZ.2019.2941697
[145]	Wu D R, Yuan Y, Huang J, Tan Y H. Optimize TSK fuzzy systems for regression problems: Minibatch gradient descent with regularization, DropRule, and AdaBound (MBGD-RDA). IEEE Transactions on Fuzzy Systems, 2020, 28(5): 1003−1015 doi: 10.1109/TFUZZ.2019.2958559
[146]	Cui Y Q, Wu D R, Huang J. Optimize TSK fuzzy systems for classification problems: mini-batch gradient descent with uniform regularization and batch normalization. IEEE Transactions on Fuzzy Systems, 2020, DOI: 10.1109/TFUZZ.2020.2967282
[147]	Zhou Z H, Feng J. Deep forest. National Science Review, 2019, 6(1): 74−86 doi: 10.1093/nsr/nwy108
[148]	Ying H. General interval type-2 Mamdani fuzzy systems are universal approximators. In: Proceedings of the 2008 Annual Meeting of the North American Fuzzy Information Processing Society. New York City, USA: IEEE, 2008.
[149]	Ying H. Interval type-2 Takagi-Sugeno fuzzy systems with linear rule consequent are universal approximators. In: Proceedings of the 2009 Annual Meeting of the North American Fuzzy Information Processing Society. Cincinnati, USA: IEEE, 2009.
[150]	Liu Z, Chen C P L, Zhang Y, Li H X. Type-2 hierarchical fuzzy system for high-dimensional data-based modeling with uncertainties. Soft Computing, 2012, 16(11): 1945−1957 doi: 10.1007/s00500-012-0867-8
[151]	Deng Y, Ren Z Q, Kong Y Y, Bao F, Dai Q H. A hierarchical fused fuzzy deep neural network for data classification. IEEE Transactions on Fuzzy Systems, 2017, 25(4): 1006−1012 doi: 10.1109/TFUZZ.2016.2574915