Hybrid Integrated Modeling Based Adaptive Nonlinear Predictive Control of Silicon Single Crystal Diameter
-
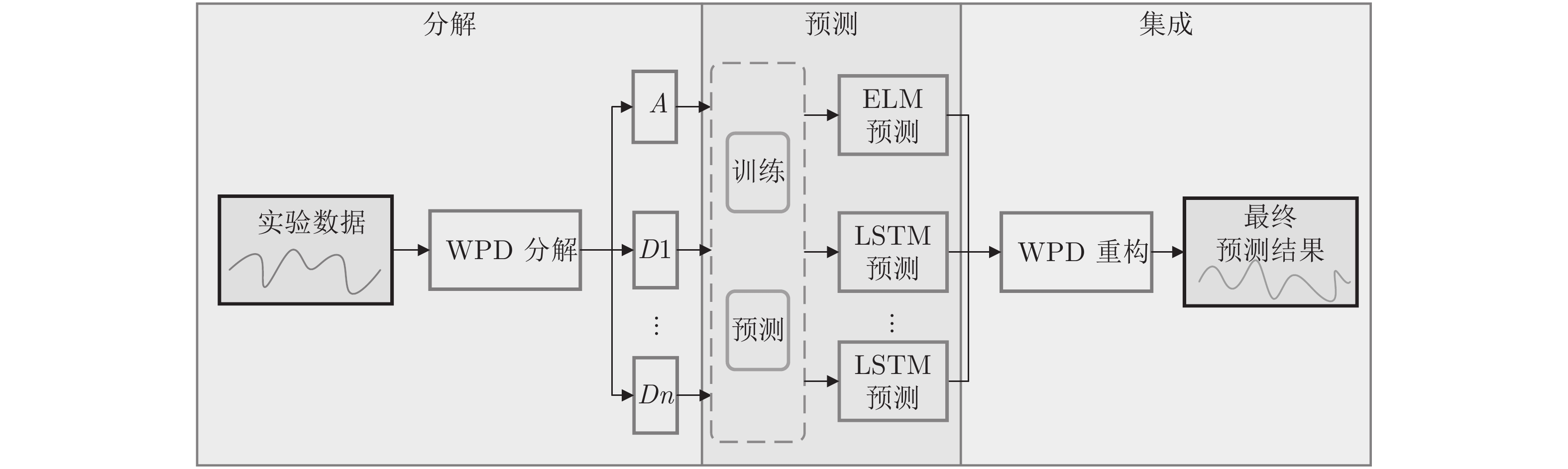
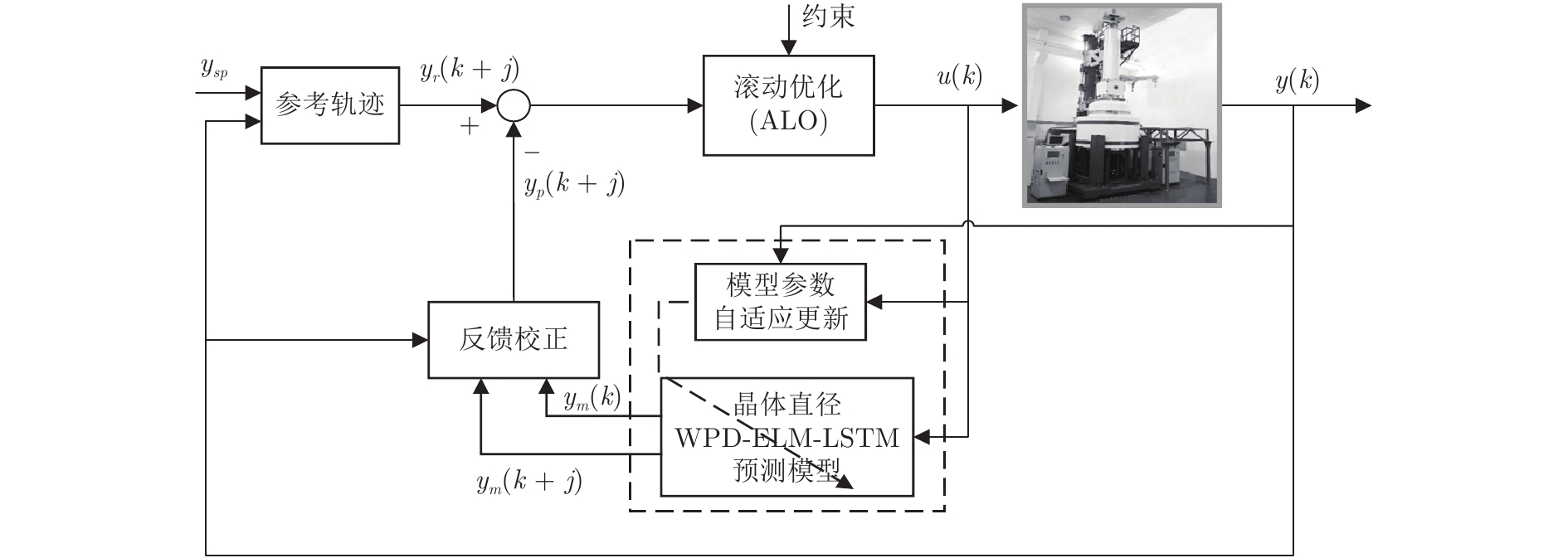
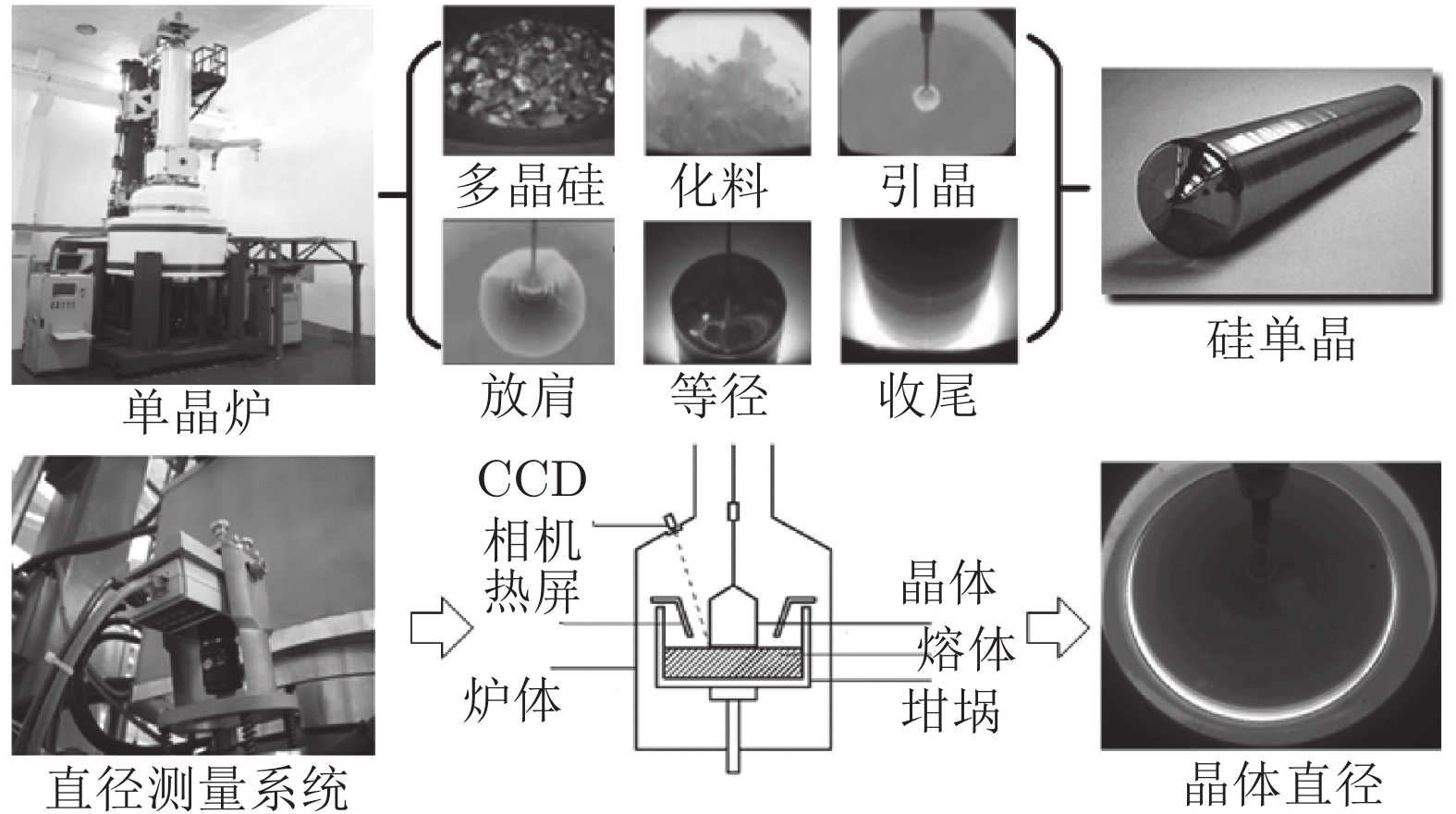
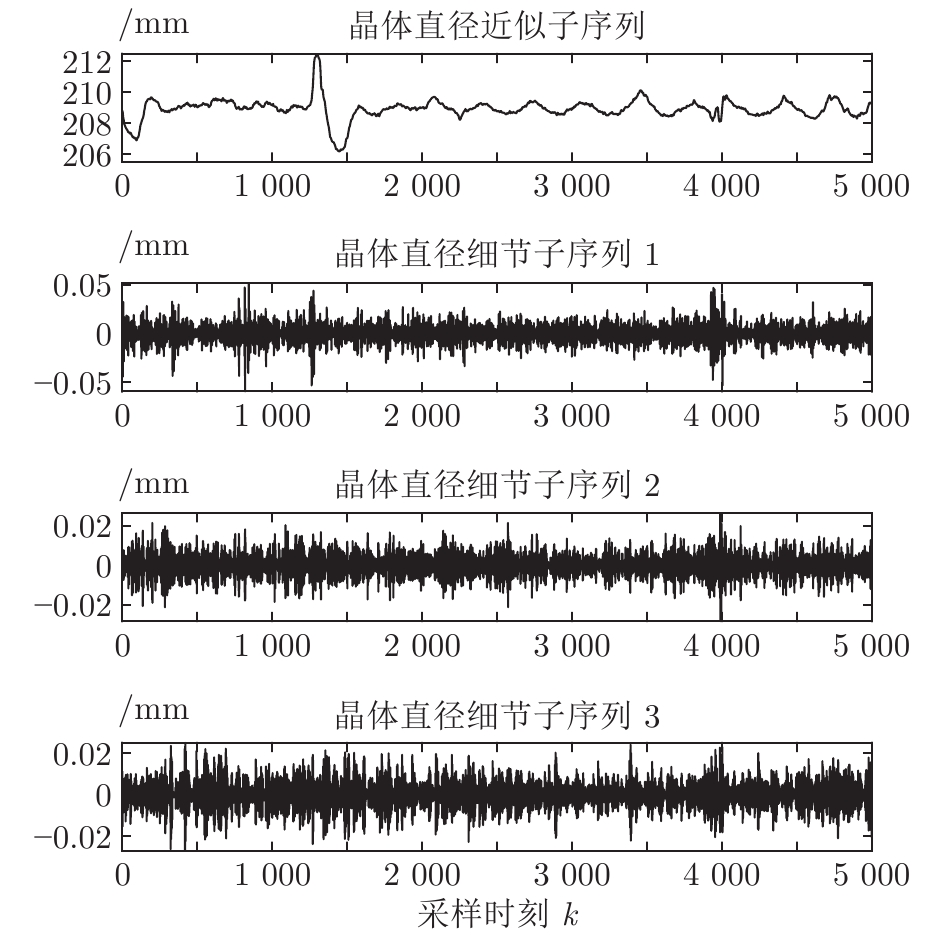
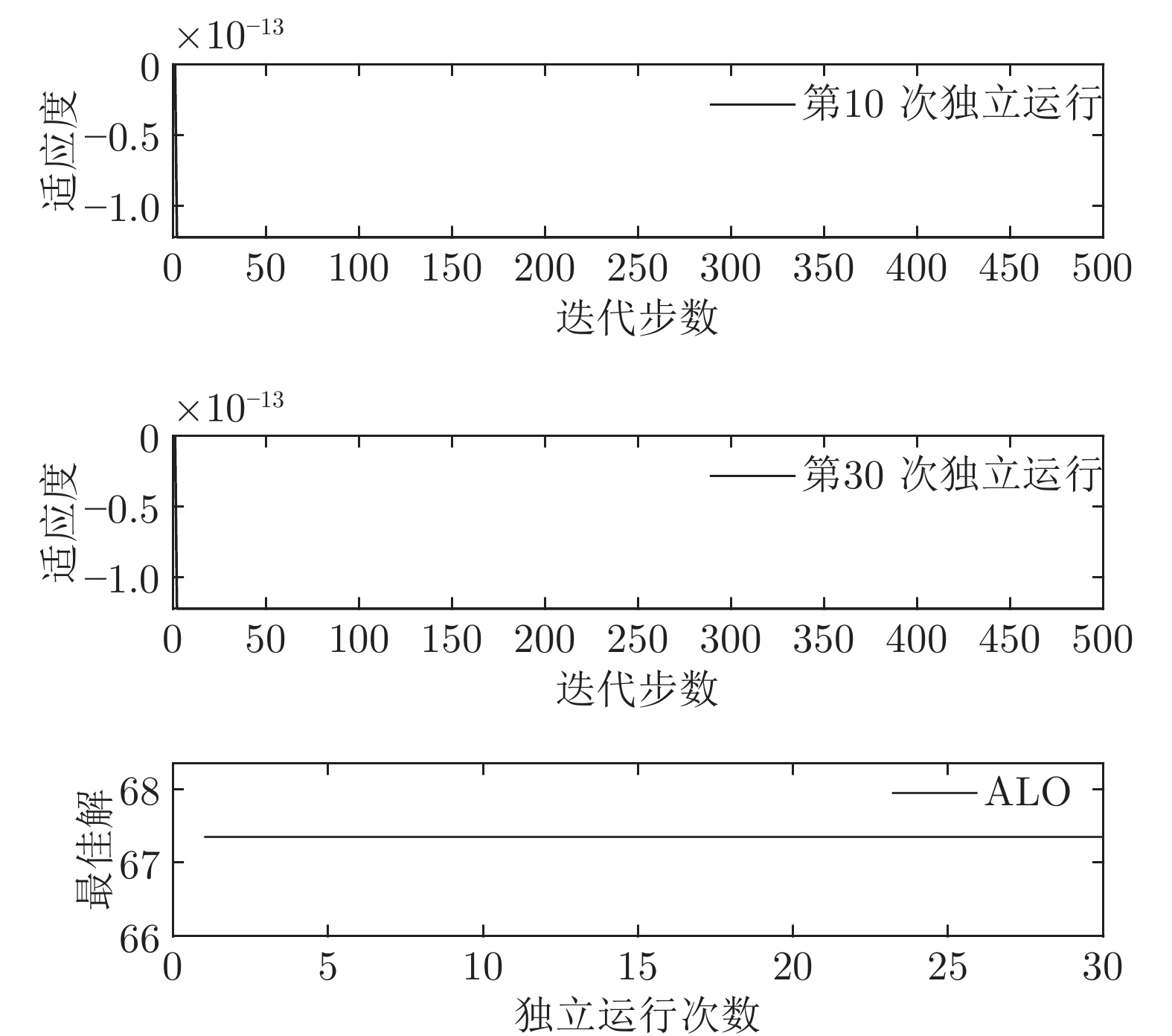
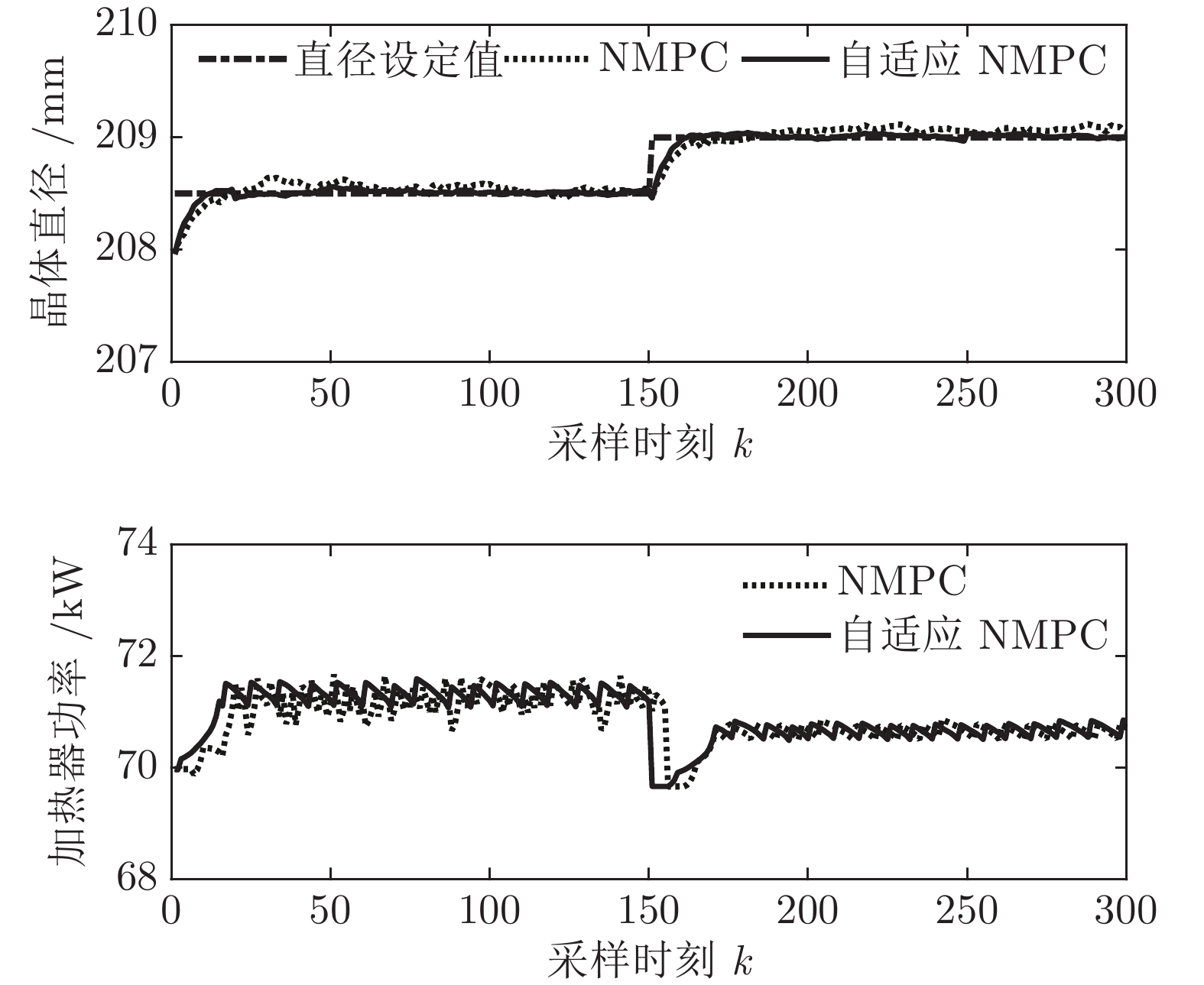
摘要: 大尺寸、电子级直拉硅单晶生长过程中物理变化复杂、多场多相耦合、模型不确定且存在大滞后和非线性等特性, 因此如何实现硅单晶直径控制是一个具有理论意义和实际价值的问题. 本文结合工程实际提出一种基于混合集成建模的晶体直径自适应非线性预测控制方法. 首先, 为了准确辨识晶体直径模型, 提出基于互相关函数的时滞优化估计方法和基于Lipschitz商准则与模型拟合优度的模型阶次辨识方法; 其次, 基于“分而治之”原理构建晶体直径混合集成模型. 其中, 采用小波包分解(Wavelet packet decomposition, WPD)方法将原始数据分解成若干个子序列, 以减少其非平稳性和随机噪声. 极限学习机(Extreme learning machine, ELM)和长短时记忆网络(Long-short-term memory networks, LSTM)分别建立近似(低频)子序列和细节(高频)子序列的预测模型, 最终晶体直径预测输出由各子序列的预测结果汇总而成; 然后, 针对晶体直径混合集成模型失配问题以及目标函数难以求解问题, 提出一种基于蚁狮优化(Ant lion optimizer, ALO)的自适应非线性预测控制策略. 最后, 基于工程实验数据仿真分析, 验证了所提建模及控制方法的有效性.
-
关键词:
- 直拉硅单晶生长 /
- 直径控制 /
- 混合集成建模 /
- 模型辨识 /
- 自适应非线性预测控制
Abstract: Large-scale, electronic-grade Czochralski silicon single crystal growth process has complex physical changes, multi-field and multi-phase coupling, model uncertainty, and large lag and nonlinear characteristics. Therefore, how to control the silicon single crystal diameter is a problem of theoretical significance and practical value. Based on the engineering reality, this paper proposes a crystal diameter adaptive nonlinear predictive control method based on hybrid integrated modeling. Firstly, in order to accurately identify the crystal diameter model, a time-delay optimization estimation method based on cross-correlation function and a model order identification method based on Lipschitz quotient criterion and goodness-of-fit of the models are proposed; Secondly, based on the principle of "divide and conquer", a hybrid integrated model of crystal diameter is constructed. Here, wavelet packet decomposition (WPD) is used to decompose the raw data into several subsequences to reduce its non-stationarity and random noise. Extreme learning machines (ELM) and long-short-term memory networks (LSTM) establish prediction models of approximate (low-frequency) subsequences and detail (high-frequency) subsequences, respectively. The final crystal diameter prediction output is summarized by the prediction results of each subsequence; Then, in view of the mismatch of the crystal diameter hybrid integrated model and the difficulty of solving the objective function, a adaptive nonlinear predictive control strategy based on ant lion optimizer (ALO) is proposed. Finally, the effectiveness of the proposed modeling and control method is verified by the simulation analysis of engineering experimental data. -
图 2 基于WPD-ELM-LSTM的混合集成建模框架
Fig. 2 Hybrid integrated modeling framework based on WPD-ELM-LSTM
图 3 基于WPD-ELM-LSTM的晶体直径自适应NMPC结构
Fig. 3 Crystal diameter adaptive NMPC structure based on WPD-ELM-LSTM
图 4 Cz法硅单晶生长过程和晶体直径测量系统
Fig. 4 Cz silicon single crystal growth process and crystal diameter measurement system
图 5 原始晶体直径与加热器功率实验数据
Fig. 5 Experimental data of raw crystal diameter and heater power
图 8 不同建模方法的晶体直径预测效果及评价指标对比
Fig. 8 Comparison of prediction effect and evaluation index of crystal diameter by different modeling methods
图 9 自适应NMPC和常规NMPC的晶体直径设定值跟踪效果
Fig. 9 Crystal diameter setpoint tracking effect of adaptive NMPC and conventional NMPC
图 10 晶体直径控制性能指标和模型参数估计性能指标收敛曲线
Fig. 10 Convergence curve of crystal diameter control performance index and model parameter estimation performance index
图 11 所提自适应NMPC与常规PID的晶体直径控制结果
Fig. 11 The crystal diameter control results of the proposed adaptive NMPC and conventional PID
图 12 时滞阶次变化时所提自适应NMPC与常规PID的晶体直径控制结果
Fig. 12 Crystal diameter control results of adaptive NMPC and conventional PID for delay order variation
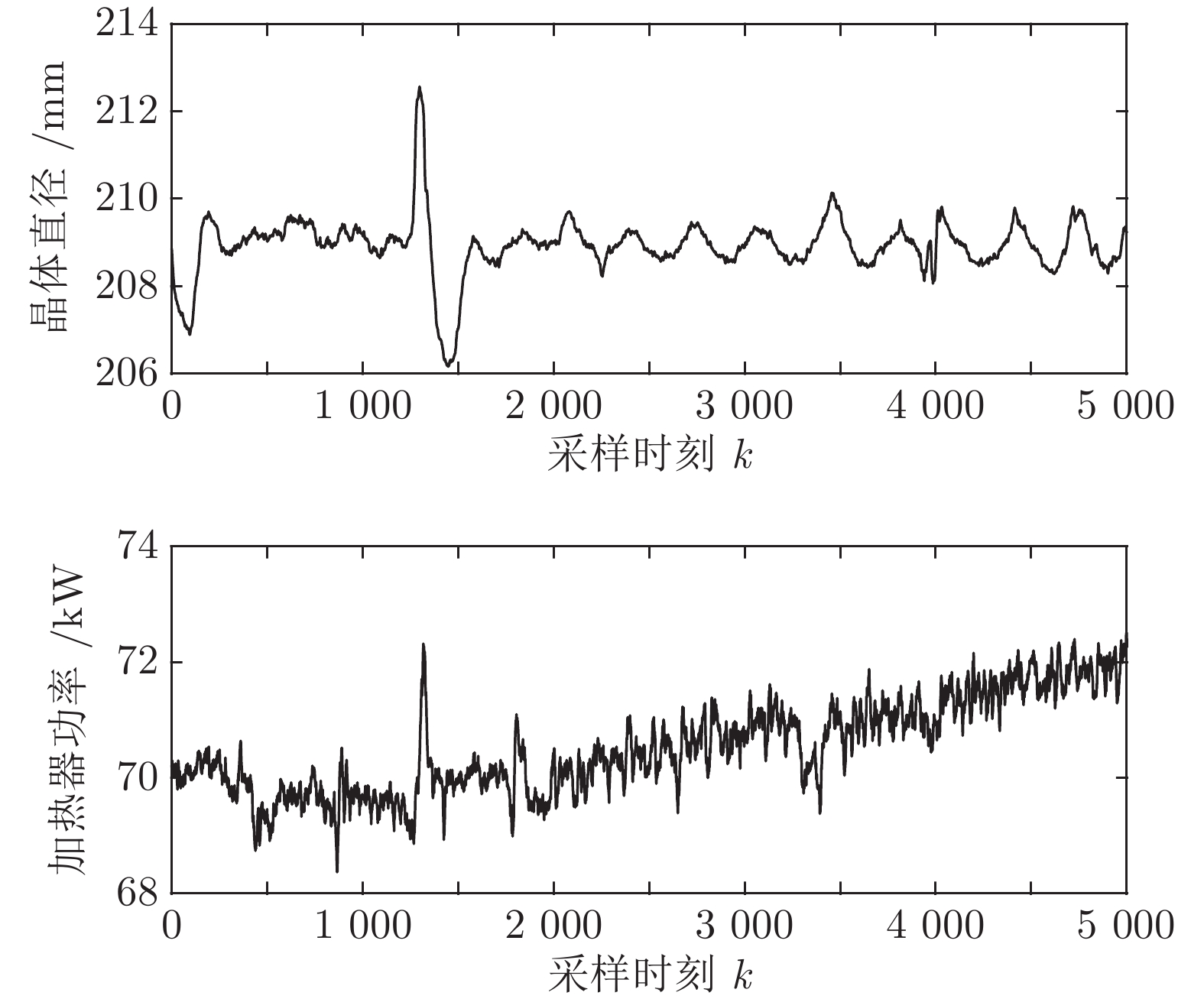
表 1 原始实验数据集的统计特性
Table 1 Statistical characteristics of the raw experimental data set
数据集 数量 Mean Max Min Std 晶体直径 (mm) 总样本 5 000 208.92 212.57 206.16 0.66 训练集 3 800 208.92 212.57 206.16 0.72 测试集 1 200 208.92 209.83 208.06 0.41 加热器功率 (kW) 总样本 5 000 70.52 72.51 68.37 0.80 训练集 3 800 70.20 72.32 68.37 0.59 测试集 1 200 71.56 72.51 70.44 0.40 
下载: 导出CSV
表 2 基于Lipschitz商准则的输入变量个数辨识结果
Table 2 Identification results of the number of input variables based on Lipschitz quotient criterion
$\Gamma (m + 1,m)$ $\Gamma (4,3)$ $\Gamma (5,4)$ $\Gamma (6,5)$ $\Gamma (7,6)$ $\Gamma (8,7)$ $\Gamma (9,8)$ $\Gamma (10,9)$ $\Gamma (11,10)$ 指标值 0.0145 0.0105 0.0088 0.0071 0.0141 0.0071 0.0033 0.0003
下载: 导出CSV
表 3 不同阶次组合的模型拟合优度结果
Table 3 Goodness-of-fit of the models with different order combinations
不同阶次组合 $({n_u},{n_y})$ (1,3) (2,2) (3,1) 模型拟合优度值Fit 99.9132 99.9085 99.9090
下载: 导出CSV
表 4 模型性能评价指标
Table 4 Model performance evaluation index
指标 定义 公式 MAE 平均绝对值误差 ${\rm MAE} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\left| {f(i) - \hat f(i)} \right|} $ MAPE 平均绝对百分
比误差${\rm MAPE} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\left| {\frac{ {f(i) - \hat f(i)} }{ {f(i)} } } \right|} \times 100{\rm{\% } }$ RMSE 均方根误差 ${\rm RMSE} = \sqrt {\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N { { {(f(i) - \hat f(i))}^2} } } $
下载: 导出CSV
表 5 不同预测方法的参数设置
Table 5 Parameter setting of different prediction methods
预测方法 参数设置 ELM 20 个隐含节点数, 激活函数 sigmoid LSTM 200 个隐含节点数, 学习率 0.005, 训练轮次 200 WPD-ELM 20 个隐含节点数, 激活函数 sigmoid WPD-LSTM 200 个隐含节点数, 学习率 0.005, 训练轮次 200 WPD-ELM-LSTM ELM: 27 个隐含节点数, 激活函数 sigmoid; LSTM: 185 个隐含节点数, 学习率 0.005, 训练轮次 200
下载: 导出CSV
表 6 不同预测模型的晶体直径预测指标
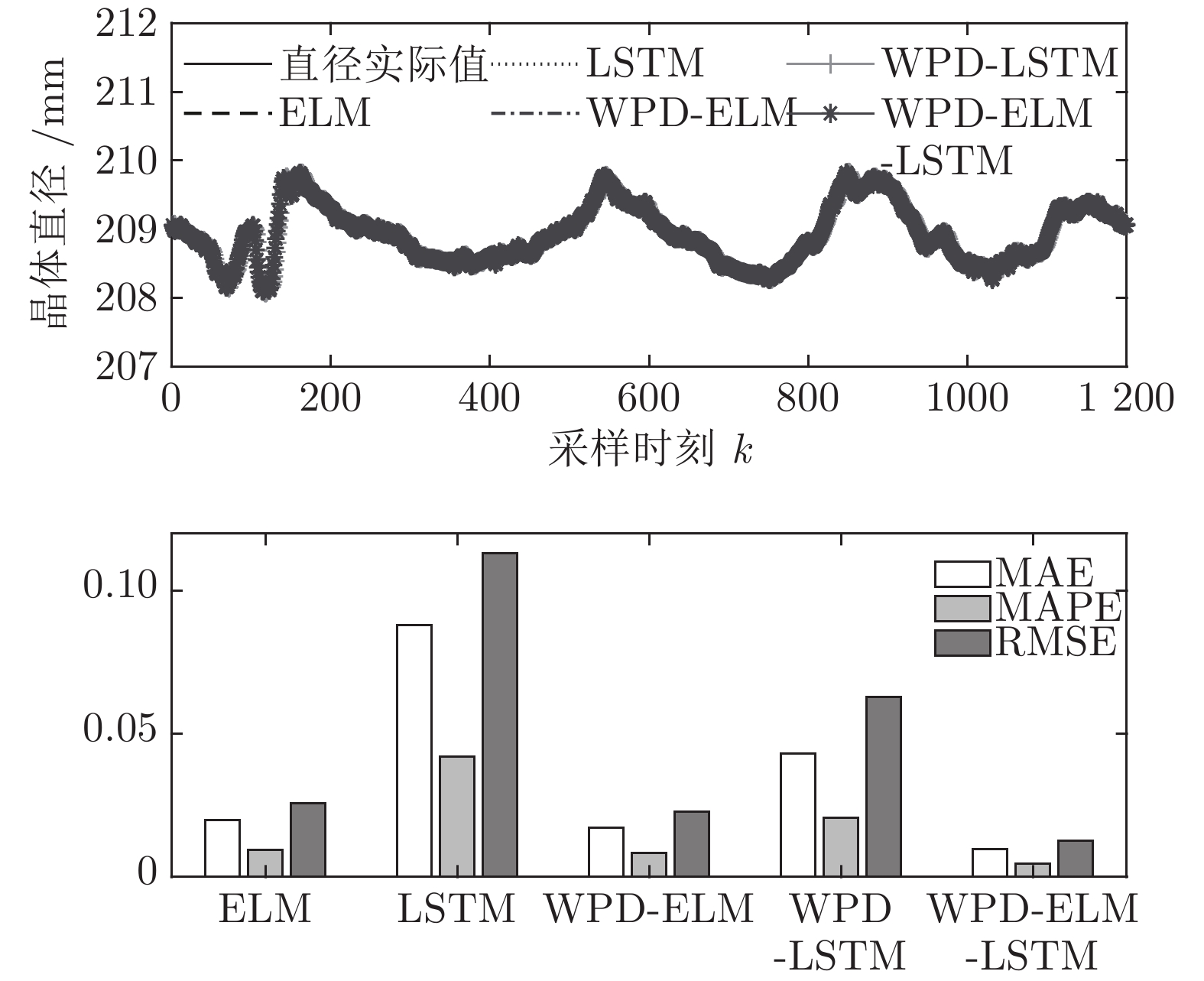
Table 6 Prediction index of crystal diameter based on different prediction models
模型 MAE (mm) MAPE (%) RMSE (mm) ELM 0.0197 0.0094 0.0258 LSTM 0.0878 0.0420 0.1131 WPD-ELM 0.0172 0.0082 0.0228 WPD-LSTM 0.0431 0.0206 0.0627 WPD-ELM-LSTM 0.0096 0.0046 0.0125
下载: 导出CSV
表 7 不同晶体直径预测模型的训练计算时间
Table 7 Training calculation time of different crystal diameter prediction models
预测模型 训练计算时间 (s) ELM 0.0828 LSTM 304.4786 WPD-ELM 0.2752 WPD-LSTM 972.6920 WPD-ELM-LSTM 601.1670
下载: 导出CSV
表 8 基于不同预测模型的晶体直径预测控制计算时间
Table 8 Calculation time of crystal diameter predictive control based on different prediction models
预测模型 平均控制量更新时间 (s) ELM (常规NMPC) 0.4512 LSTM (常规NMPC) 0.4899 WPD-ELM-LSTM (常规NMPC) 0.6841 WPD-ELM-LSTM (自适应NMPC) 7.3113
下载: 导出CSV
-
[1] 刘丁. 直拉硅单晶生长建模与控制. 北京: 科学出版社, 2015, 1−252Liu Ding. Modeling and control of Czochralski silicon single crystal growth. Beijing: Science Press, 2015, 1−252 [2] Duffar T. Crystal Growth Processes Based on Capillarity: Czochralski, Floating Zone, Shaping and Crucible Techniques. New York, NY, USA: Wiley, 2010, 115−199 [3] 刘丁, 赵小国, 赵跃. 直拉硅单晶生长过程建模与控制研究综述. 控制理论与应用, 2017, 34(1): 1−12Liu Ding, Zhao Xiao-Guo, Zhao Yue. A review of growth process modeling and control of Czochralski silicon single crystal. Control Theory & Applications, 2017, 34(1): 1−12 [4] Voronkov V V. Grown-in defects in silicon produced by agglomeration of vacancies and self-interstitials. Journal of Crystal Growth, 2008, 310(7–9): 1307−1314 doi: 10.1016/j.jcrysgro.2007.11.100 [5] Neubert M, Winkler J. Nonlinear model-based control of the Czochralski process IV: Feedforward control and its interpretation from the crystal grower's view. Journal of Crystal Growth, 2014, 404(404): 210−222 [6] Satunkin G A. Mathematical modelling and control system design of Czochralski and liquid encapsulated Czochralski processes: the basic low order mathematical model. Journal of Crystal Growth, 1995, 154(1–2): 172−188 doi: 10.1016/0022-0248(95)00050-X [7] Michael A. Gevelber, George Stephanopoulos, Michael J, et al. Dynamics and control of the Czochralski process II. Objectives and control structure design. Journal of Crystal Growth, 1988, 91(1–2): 199−217 doi: 10.1016/0022-0248(88)90386-7 [8] Zinnes A E, Nevis B E, Brandle C D. Automatic diameter control of Czochralski grown crystals. Journal of Crystal Growth, 1973, 19(3): 187−192 doi: 10.1016/0022-0248(73)90108-5 [9] Zhongchao Zheng, Tatsuru Seto, Sanghong Kim, et al. A first-principle model of 300 mm Czochralski single-crystal Si production process for predicting crystal radius and crystal growth rate. Journal of Crystal Growth, 2018, 492(15): 105−113 [10] Abdollahi J, Dubljevic S. Crystal radius and temperature regulation in Czochralski crystallization process. In: Proceedings of the 2013 American Control Conference. Washington, USA: IEEE, 2013.1626−1632 [11] Winkler J, Neubert M, Rudolph J. Nonlinear model-based control of the Czochralski process I: Motivation, modeling and feedback controller design. Journal of Crystal Growth, 2010, 312(7): 1005−1018 doi: 10.1016/j.jcrysgro.2009.12.074 [12] Winkler J, Neubert M, Rudolph J. Nonlinear model-based control of the Czochralski process II: Reconstruction of crystal radius and growth rate from the weighing signal. Journal of Crystal Growth, 2010, 312(7): 1019−1028 doi: 10.1016/j.jcrysgro.2009.12.073 [13] Rahmanpour P, Saelid S, Hovd M, et al. Nonlinear model predictive control of the czochralski process. IFAC Papersonline, 2016, 49(20): 120−125 doi: 10.1016/j.ifacol.2016.10.107 [14] Neubert M, Winkler J. Nonlinear model-based control of the Czochralski process III: Proper choice of manipulated variables and controller parameter scheduling. Journal of Crystal Growth, 2012, 360(1): 3−11 [15] Liu D, Zhang N, Jiang L, et al. Nonlinear generalized predictive control of the crystal diameter in CZ-Si crystal growth process based on stacked sparse autoencoder. IEEE Transactions on Control Systems Technology, 2020, 28(3): 1132−1139 [16] Hou Z, Chi R, Gao H. An overview of dynamic linearization based data-driven control and applications. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4076−4090 doi: 10.1109/TIE.2016.2636126 [17] Zhou P, Song H D, Wang H, Chai T Y. Data-driven nonlinear subspace modeling for prediction and control of molten iron quality indices in blast furnace ironmaking. IEEE Transactions on Control Systems Technology, 2017, 25(5): 1761−1774 [18] Ren Y, Zhang L, Suganthan P N. Ensemble classification and regression-recent developments, applications and future directions. IEEE Computational Intelligence Magazine, 2016, 11(1): 41−53 doi: 10.1109/MCI.2015.2471235 [19] Zhang Y H, Wang H, Hu Z J, et al. A hybrid short-term wind speed forecasting model based on ensemble empirical mode decomposition and improved extreme learning machine. Power System Protection and Control, 2014, 42(10): 29−34 [20] Wang S, Zhang N, Wu L, et al. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renewable Energy, 2016, 94: 629−636 doi: 10.1016/j.renene.2016.03.103 [21] Mayne, David Q. Model predictive control: Recent developments and future promise. Automatica, 2014, 50(12): 2967−2986 doi: 10.1016/j.automatica.2014.10.128 [22] 席裕庚, 李德伟, 林姝. 模型预测控制—现状与挑战. 自动化学报, 2013, 39(3): 222−236 doi: 10.1016/S1874-1029(13)60024-5Xi Yu-Geng, Li De-Wei, Lin Shu. Model predictive control — status and challenges. Acta Automatica Sinica, 2013, 39(3): 222−236 doi: 10.1016/S1874-1029(13)60024-5 [23] Feng K, Lu J, Chen J. Nonlinear model predictive control based on support vector machine and genetic algorithm. Chinese Journal of Chemical Engineering, 2015, 23(12): 2048−2052 doi: 10.1016/j.cjche.2015.10.009 [24] Nery J G A, Martins M A F, Ricardo K. A PSO-based optimal tuning strategy for constrained multivariable predictive controllers with model uncertainty. ISA Transactions, 2014, 53(2): 560−567 [25] Mirjalili S. The ant lion optimizer. Advances in Engineering Software, 2015, 83(C): 80−98 [26] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: theory and applications. Neurocomputing, 2006, 70(1): 489−501 [27] Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification. IEEE Transactions on Systems Man & Cybernetics Part B, 2012, 42(2): 513−529 [28] Jesus G, Wen Y. Non-linear system modeling using LSTM neural network. IFAC Papersonline, 2018, 51(13): 485−489 doi: 10.1016/j.ifacol.2018.07.326 [29] Wang Y. A new concept using LSTM neural networks for dynamic system identification. In: Proceedings of the 2017 American Control Conference. Seattle, WA, USA: IEEE, 2017. 5324−5329 [30] Tang Y, Li Z, Guan X. Identification of nonlinear system using extreme learning machine based Hammerstein model. Communications in Nonlinear Science & Numerical Simulation, 2014, 19(9): 3171−3183 [31] 周平, 刘记平. 基于数据驱动多输出 ARMAX 建模的高炉十字测温中心温度在线估计. 自动化学报, 2018, 44(3): 552−561Zhou Ping, Liu Ji-Ping. Data-driven multi-output ARMAX modeling for online estimation of central temperatures for cross temperature measuring in blast furnace ironmaking. Acta Automatica Sinica, 2018, 44(3): 552−561 [32] He X, Asada H. A new method for identifying orders of input-output models for nonlinear dynamic systems. American Control Conference. San Francisco, CA, USA: IEEE, 1993. [33] 梁炎明. 基于数据驱动的硅单晶生长过程控制研究[博士学位论文], 西安理工大学, 中国, 2014Liang Yan-Ming. Data-driven Based Growth Control for Silicon Single Crystal [Ph. D. dissertation], Xi'an University of Technology, China, 2014 [34] 戴鹏, 周平, 梁延灼, 等. 基于多输出最小二乘支持向量回归建模的自适应非线性预测控制及应用. 控制理论与应用, 2019, 36(1): 45−54Dai Peng, Zhou Ping, Liang Yan-Zhuo, et al. Multi-output least squares support vector regression modeling based adaptive nonlinear predictive control and its application. Control Theory & Applications, 2019, 36(1): 45−54 [35] 刘丁, 张新雨, 陈亚军. 基于多目标人工鱼群算法的硅单晶直径检测图像阈值分割方法. 自动化学报, 2016, 42(3): 113−124Liu Ding, Zhang Xin-Yu, Chen Ya-Jun. Monocrystalline silicon diameter detection image threshold segmentation method using multi-objective artiflcial flsh swarm algorithm. Acta Automatica Sinica, 2016, 42(3): 113−124 -
计量
- 文章访问数: 6521
- HTML全文浏览量: 1343
- PDF下载量: 193
- 被引次数: 0
