-
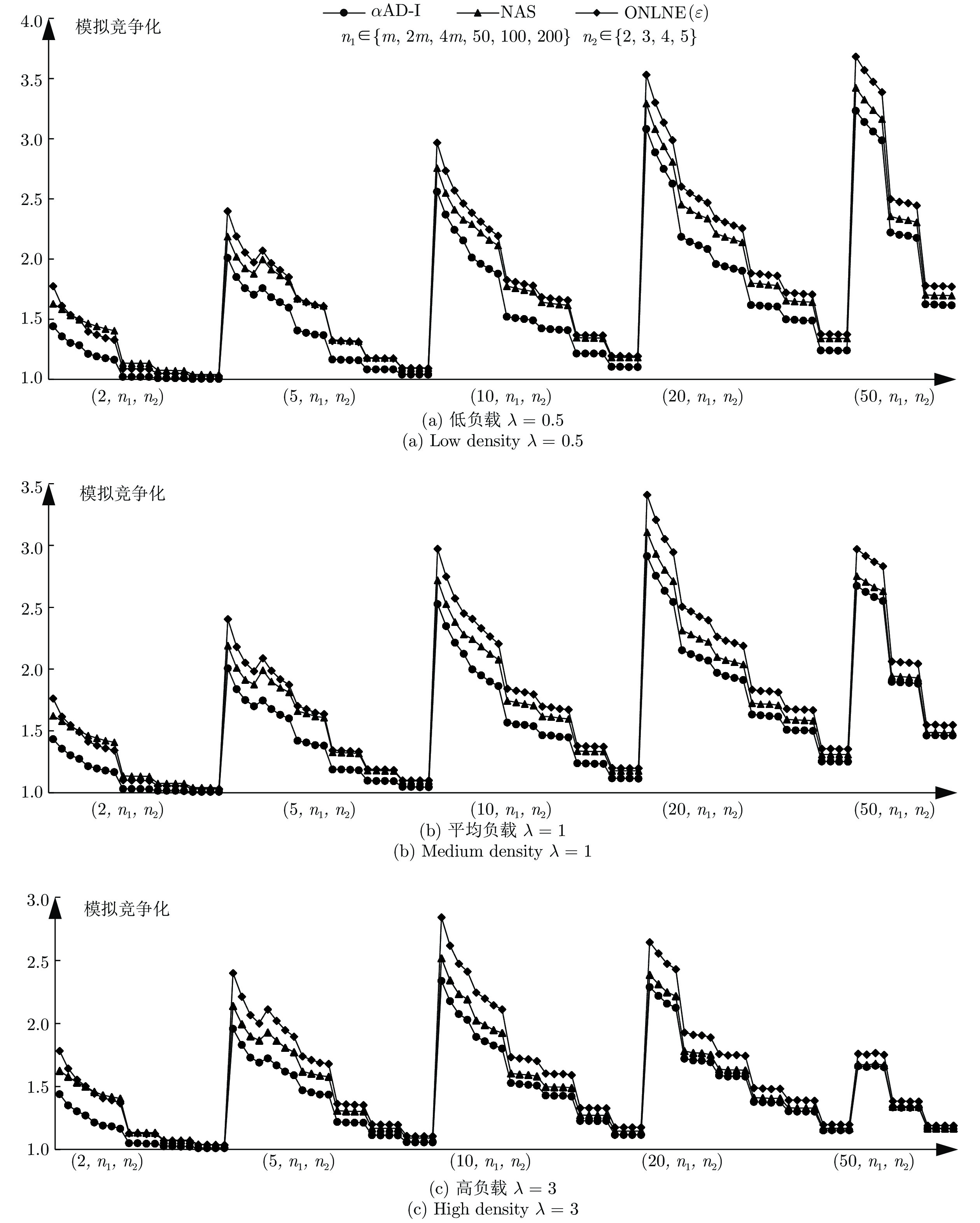
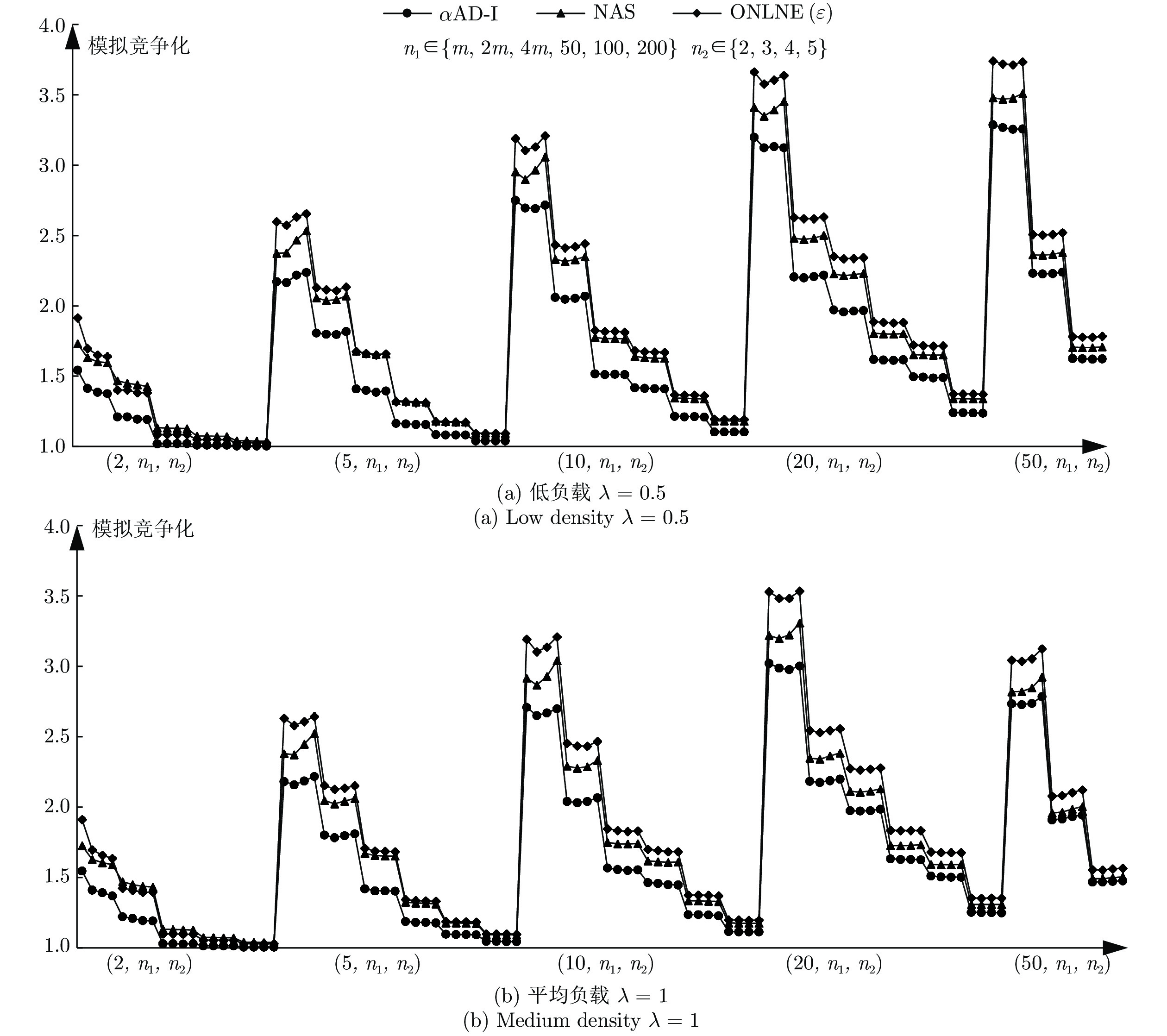
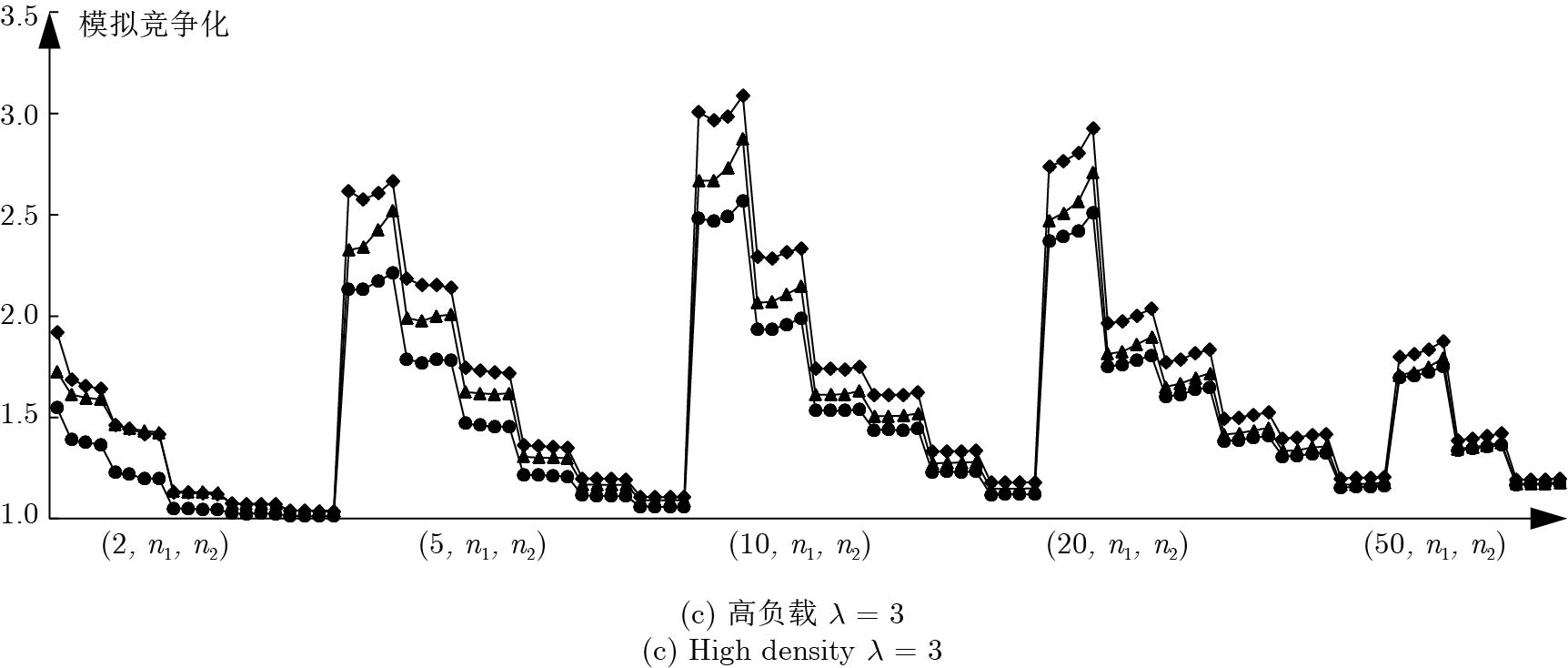
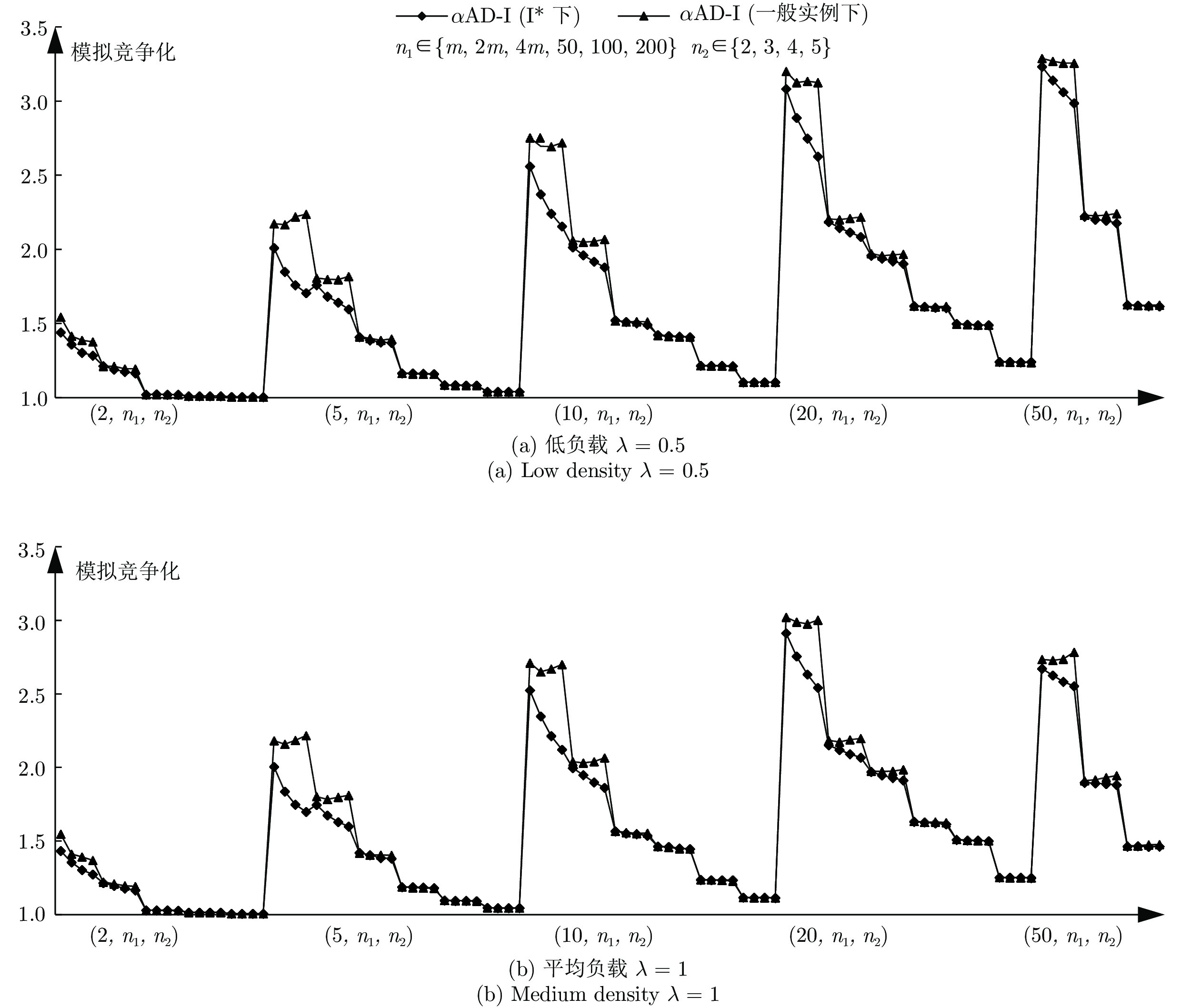
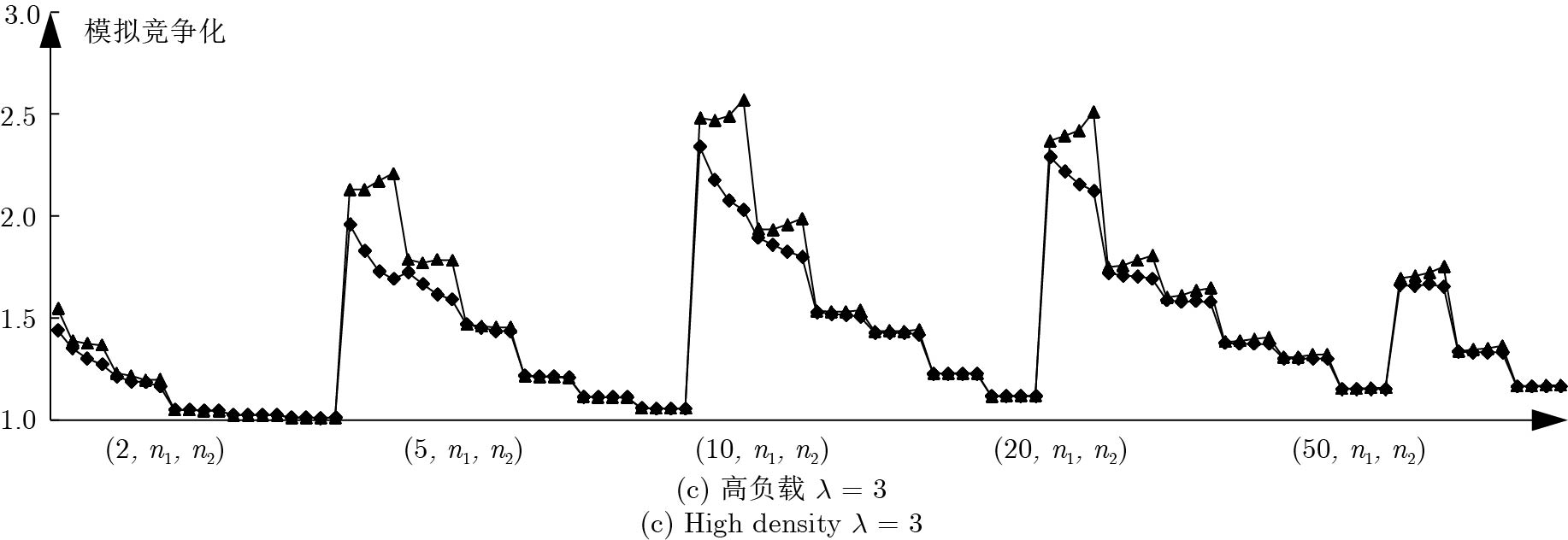
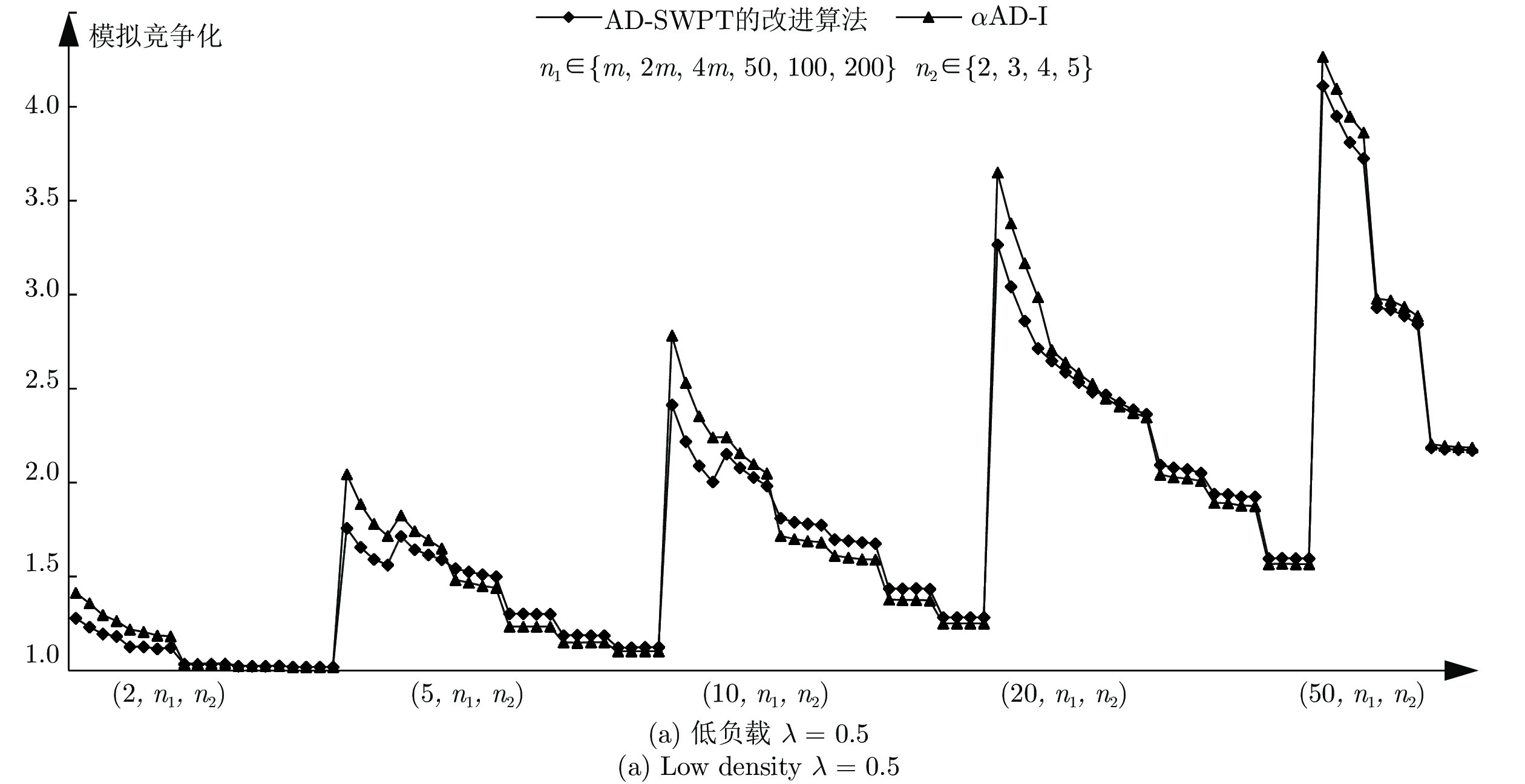
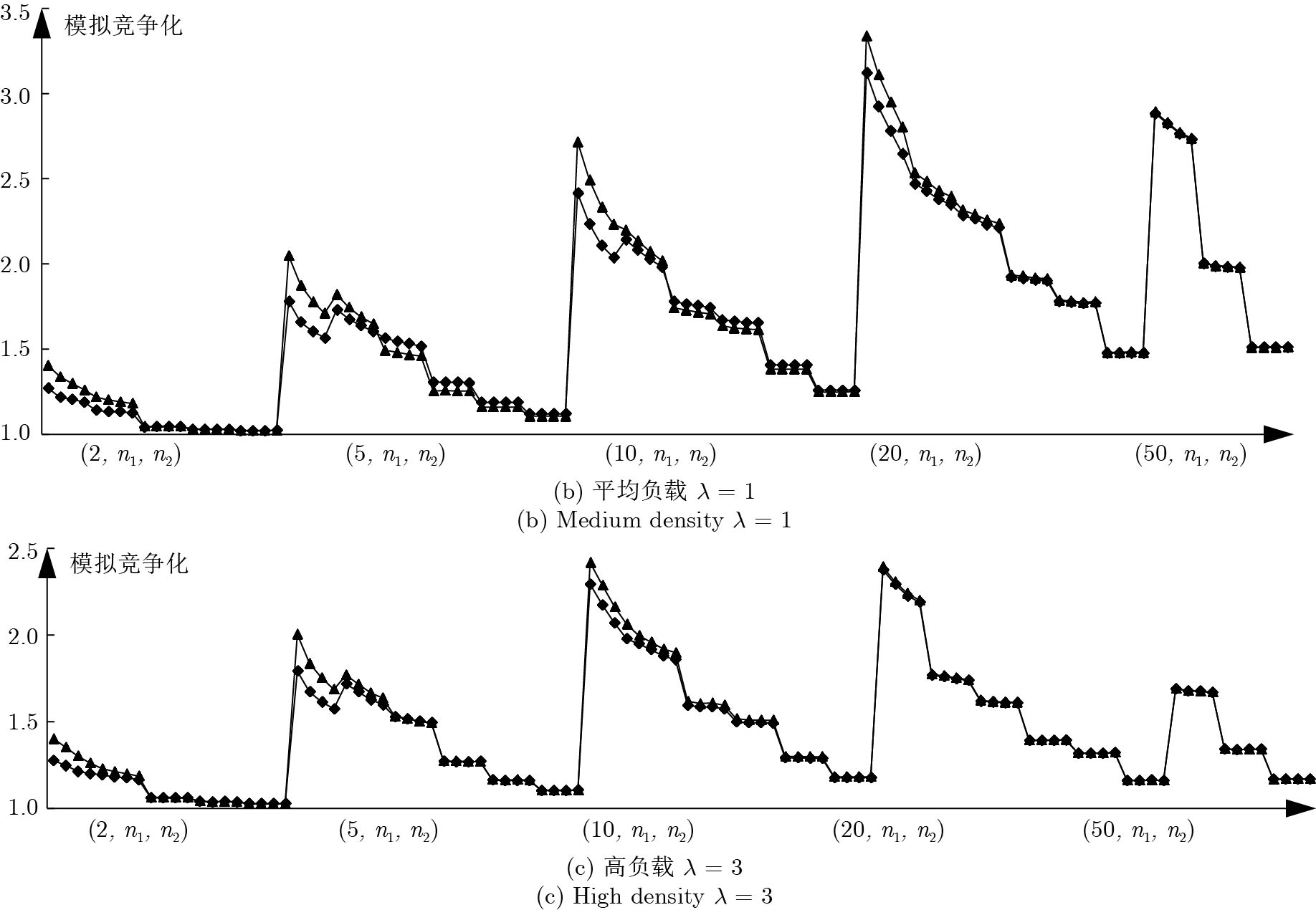
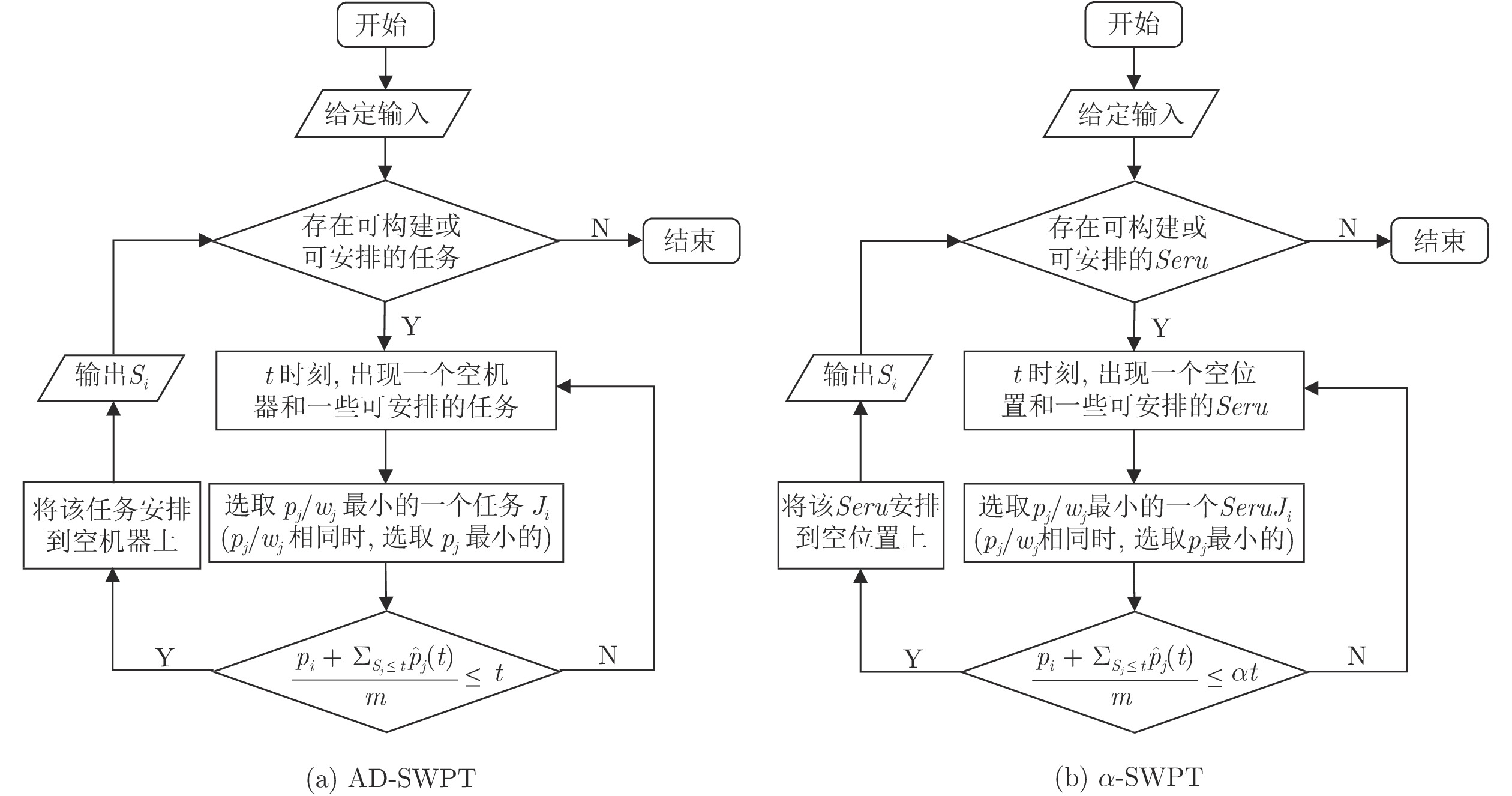
摘要: 随着大规模定制的市场需求日趋显著, 赛如生产系统(Seru production system, SPS)应运而生, 逐渐成为研究和应用领域的热点. 本文针对带有资源冲突的Seru在线并行调度问题进行研究, 即需要在有限的空间位置上安排随动态需求而构建的若干Seru, 以总加权完工时间最小为目标, 决策Seru的构建顺序及时间. 先基于平均延迟最短加权处理时间(Average delayed shortest weighted processing time, AD-SWPT)算法, 针对其竞争比不为常数的局限性, 引入调节参数, 得到竞争比为常数的无资源冲突的Seru在线并行调度算法. 接下来, 引入冲突处理机制, 得到有资源冲突的Seru在线并行调度算法, αAD-I (α-average delayed shortest weighted processing time-improved)算法, 特殊实例下可通过实例归约的方法证明其竞争比与无资源冲突的情况相同. 最后, 通过实验, 验证了在波动的市场环境下算法对于特殊实例与一般实例的优越性.Abstract: With the remarkably increase of mass customization, there comes the seru production system (SPS), which has become a hotspot in both the research and the application fields. This paper discusses the online parallel scheduling problem of serus with resource conflicts, which aims at scheduling serus that are generated with dynamic demands on limited space to minimize the total weighted completion time. First, we consider online parallel scheduling of serus without resource conflicts. Based on the average delayed shortest weighted processing time (AD-SWPT) algorithm, an adjustment parameter is introduced and an optimization algorithm with a constant competitive ratio is proposed. Then for online parallel scheduling of serus with resource conflicts, an α-average delayed shortest weighted processing time-improved (αAD-I) algorithm is proposed, whose competitive ratio is proved to be the same as the one without resource conflicts in special cases via instance reduction. Computational experiments are implemented to test and verify the superiority of our algorithm under both special instances and general instances.
-
表 1 基本符号说明
Table 1 Basic symbolic explanation
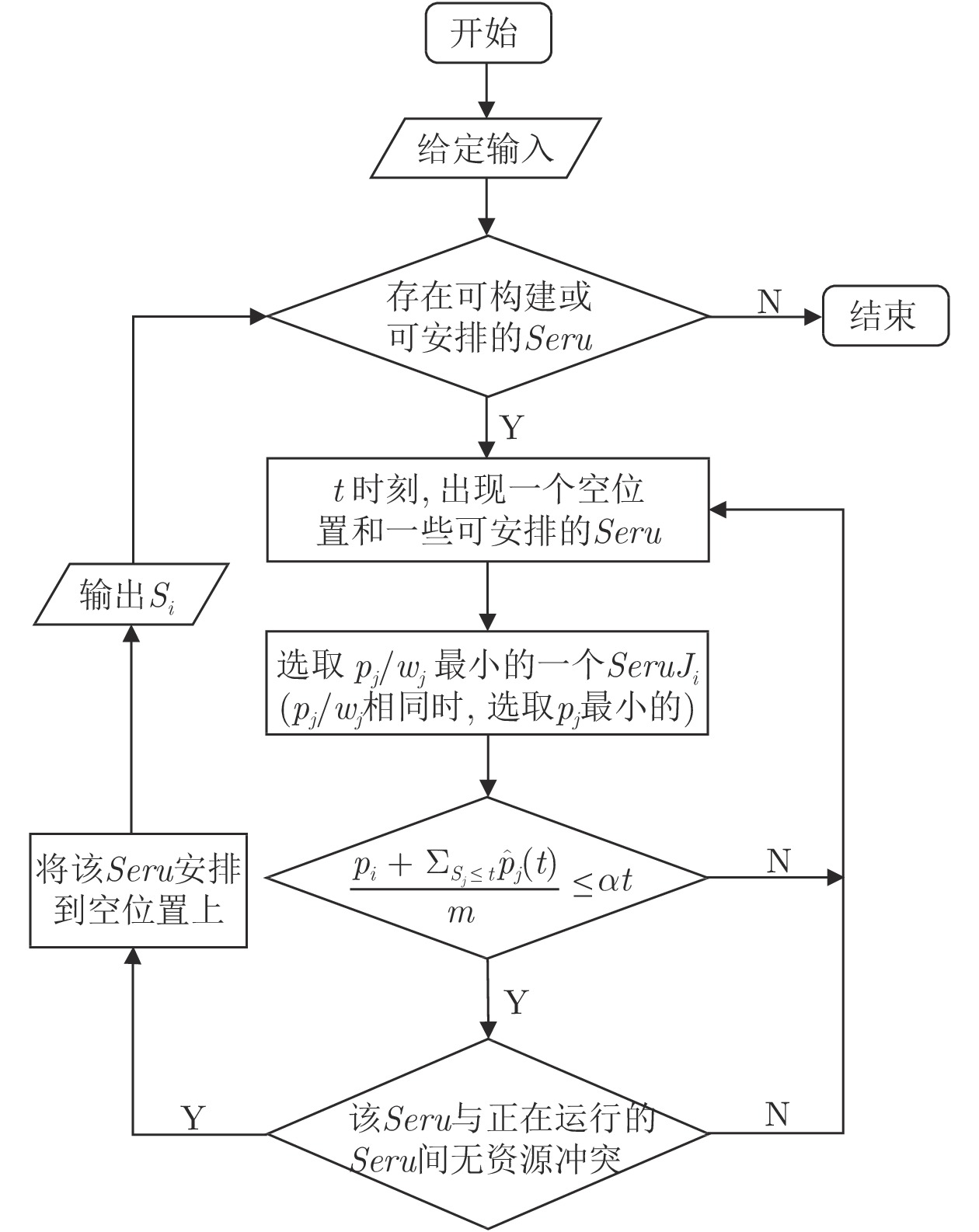
符号 说明 $t$ 当前时刻 $\hat{p}_j(t)$ 对于一个可行的安排方案, 在时刻$t$, 任务/$Seru$ $J_j$还剩余的处理时间, 若在时刻$t$, 该任务/$Seru$还未开始运作, 那么$\hat{p}_j(t)=p_j$ $\sigma(\cdot)$ 一般实例下, 应用相应算法所得到的安排方案, 也用于表示对应的目标值, 在本文中即为总加权完工时间$\displaystyle\sum w_j C_j$ $S_j$ 任务/$Seru$ $J_j$在安排方案$\sigma(\cdot)$中的构建时间 $C_j$ 任务/$Seru$ $J_j$在安排方案$\sigma(\cdot)$中的完工时间 ${\text{π}}(\cdot)$ 一般实例下, 应用最优离线算法所得到的安排方案, 也用于表示对应的目标值, 在本文中即为总加权完工时间$\displaystyle\sum w_j C_j$ 表 2 无冲突时的特殊实例符号说明
Table 2 Symbolic explanation of four special instances without conflicts
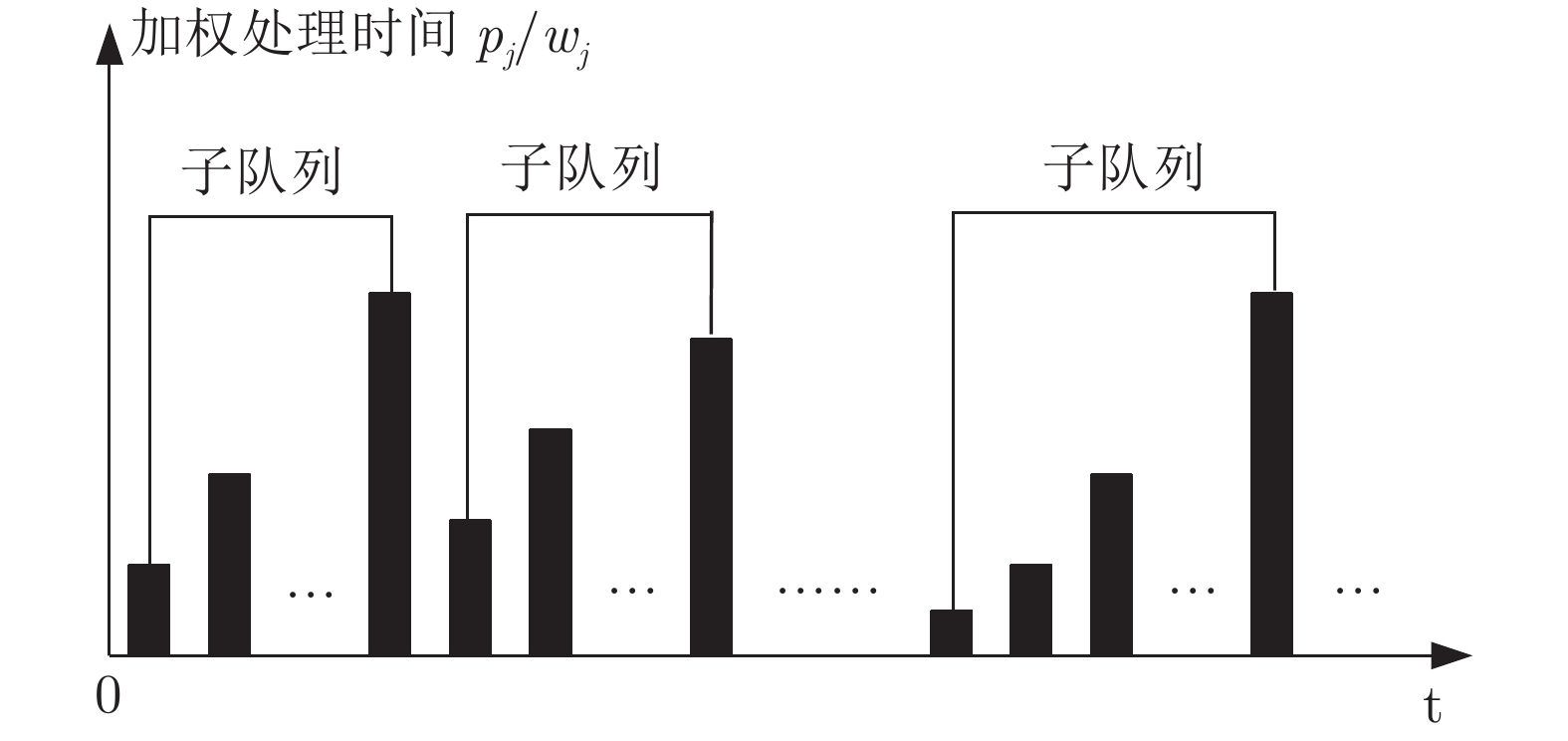
符号 说明 $I_1$ 由$\alpha$AD-SWPT 算法生成的安排方案满足在所有的位置中, 最早的 SPoint 和最晚的 EPoint 之间, 不存在任何时刻$t$所有位置都闲置的一类实例 $I'_1$ 满足$I_1$的结构, 且满足在$\alpha$AD-SWPT 算法生成的安排方案下, 最后一个子队列中所有$Seru$的加权处理时间相同的一类实例 $I_2$ 满足$I_1$的结构, 且满足所有$Seru$的加权处理时间相同的一类实例 $I_3$ 满足$I_1$的结构, 且满足在$\alpha$AD-SWPT 算法生成的安排方案下, 最后一个子队列中所有$Seru$的权重无穷大的一类实例 表 3 有冲突时的特殊实例符号说明
Table 3 Symbolic explanation of four special instances with conflicts
符号 说明 $F$ 冲突集合, 实例中所有带有资源冲突的$Seru$的集合 $I^*$ 冲突集合$F$中, 先构建的$Seru$与后构建的$Seru$完工时间的比值总是不大于$(1+1/m)/2$的一类实例 $I^*_2$ 满足$I^*$的结构, $\alpha$AD-I 算法生成的安排方案下, 最早的 SPoint 和最晚的 EPoint 之间, 不存在任何时刻$t$, 所有位置都闲置; 且所有$Seru$的加权处理时间相同的一类实例 $I^*_3$ 满足$I^*$的结构, $\alpha$AD-I 算法生成的安排方案下, 最早的 SPoint 和最晚的 EPoint 之间, 不存在任何时刻$t$, 所有位置都闲置; 且最后一个子队列中所有$Seru$的权重无穷大的一类实例 -
[1] Yin Y, Stecke K E, Li D N. The evolution of production systems from Industry 2.0 through Industry 4.0. International Journal of Production Research, 2018, 56(1-2): 848-861 doi: 10.1080/00207543.2017.1403664 [2] Yu Y, Sun W, Tang J F, Wang J W. Line-hybrid seru system conversion: models, complexities, properties, solutions and insights. Computers & Industrial Engineering, 2016, 103: 282-299 [3] Roth A, Singhal J, Singhal K, Tang C S. Knowledge creation and dissemination in operations and supply chain management. Production and Operations Management, 2016, 25(9): 1473-1488 doi: 10.1111/poms.12590 [4] Yin Y, Kaku I, Stecke K E. The evolution of seru production systems throughout Canon. Operations Management Education Review, 2008, 2: 27−40 [5] Liu C G, Lian J, Yin Y, Li W J. Seru Seisa-an innovation of the production management mode in Japan. Asian Journal of Technology Innovation, 2010, 18(2): 89-113 doi: 10.1080/19761597.2010.9668694 [6] Liu C G, Dang F, Li W J, Evans S, Yin Y. Production planning of multi-stage multi-option seru production systems with sustainable measures. Journal of Cleaner Production, 2015, 105: 285-299 doi: 10.1016/j.jclepro.2014.03.033 [7] 吴旭辉, 杜劭峰, 郝慧慧, 于洋, 殷勇, 李冬妮. 一种基于协同进化的流水线向Seru系统转化方法. 自动化学报, 2018, 44(6): 1015-1027Wu Xu-Hui, Du Shao-Feng, Hao Hui-Hui, Yu Yang, Yin Yong, Li Dong-Ni. A line-seru conversion approach by means of cooperative coevolution. Acta Automatic Sinica, 2018, 44(6): 1015-1027 [8] Yin Y, Stecke K E, Swink M, Kaku I. Lessons from seru production on manufacturing competitively in a high cost environment. Journal of Operations Management, 2017, 49-51: 67-76 doi: 10.1016/j.jom.2017.01.003 [9] Stecke K E, Yin Y, Kaku I. Seru production: An extension of just-in-time approach for volatile business environments. Analytical Approaches to Strategic Decsion-Making: Inter-disciplinary Considerations, IGI Global, 2014, 45−58 [10] Isa K, Tsuru T. Cell production and workplace innovation in Japan: toward a new model for Japanese manufacturing. Industrial Relations: A Journal of Economy and Society, 2002, 41(4): 548-578 doi: 10.1111/1468-232X.00264 [11] Stecke K E, Yin Y, Kaku I, Murase Y. Seru: the organizational extension of JIT for a super-talent factory. International Journal of Strategic Decision Sciences, 2012, 3(1): 106-119 doi: 10.4018/jsds.2012010104 [12] Liu C G, Yang N, Li W J, Lian J, Evans S, Yin Y. Training and assignment of multi-skilled workers for implementing seru production systems. The International Journal of Advanced Manufacturing Technology, 2013, 69(5-8): 937-959 doi: 10.1007/s00170-013-5027-5 [13] Yu Y, Tang J F, Gong J, Yin Y, Kaku I. Mathematical analysis and solutions for multi-objective line-cell conversion problem. European Journal of Operational Research, 2014, 236(2): 774-786 doi: 10.1016/j.ejor.2014.01.029 [14] Yu Y, Tang J F, Sun W, Yin Y, Kaku I. Combining local search into non-dominated sorting for multi-objective line-cell conversion problem. International Journal of Computer Integrated Manufacturing, 2013, 26(4): 316-326 doi: 10.1080/0951192X.2012.717717 [15] 贾凌云, 李冬妮, 田云娜. 基于混合蛙跳和遗传规划的跨单元调度方法. 自动化学报, 2014, 40(5): 936-948Jia Ling-Yun, Li Dong-Ni, Tian Yun-Na. An intercell scheduling approach using shuffled frog leaping algorithm and genetic programming. Acta Automatic Sinica, 2014, 40(5): 936-948 [16] 田云娜, 李冬妮, 刘兆赫, 郑丹. 一种基于动态决策块的超启发式跨单元调度方法. 自动化学报, 2016, 42(4): 524-534Tian Yun-Na, Li Dong-Ni, Li Zhao-He, Zheng Dan. A hyper-heuristic approach with dynamic decision blocks for inter-cell scheduling. Acta Automatic Sinica, 2016, 42(4): 524-534 [17] Wu Y K, Jiang B, Lu N Y. A descriptor system approach for estimation of incipient faults with application to high-speed railway traction devices. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 49(10): 2108-2118 [18] Wu Y K, Jiang B, Wang Y L. Incipient winding fault detection and diagnosis for squirrel-cage induction motors equipped on CRH trains. ISA Transactions, 2020, 99: 488−495 [19] Anderson E J, Potts C N. Online scheduling of a single machine to minimize total weighted completion time. Mathematics of Operations Research, 2004, 29(3): 686-697 doi: 10.1287/moor.1040.0092 [20] Hall L A, Schulz A S, Shmoys D B, Wein J. Scheduling to minimize average completion time: off-line and on-line approximation algorithms. Mathematics of Operations Research, 1997, 22(3): 513-544 doi: 10.1287/moor.22.3.513 [21] Megow N, Schulz A S. On-line scheduling to minimize average completion time revisited. Operations Research Letters, 2004, 32(5): 485-490 doi: 10.1016/j.orl.2003.11.008 [22] Correa J, Wagner M. LP-based online scheduling: from single to parallel machines. Mathematical Programming, 2009, 119(1): 109-136 doi: 10.1007/s10107-007-0204-7 [23] Sitters R. Efficient algorithms for average completion time scheduling. Integer Programming and Combinatorial Optimization. Berlin: Springer Berlin Heidelberg, 2010. 411−423 [24] Chakrabarti S, Phillips C A, Schulz A S, Shmoys D B, Stein C, Wein J. Improved scheduling algorithms for minsum criteria. Automata, Languages and Programming. Berlin: Springer Berlin Heidelberg, 1996. 646−657 [25] Schulz A S, Skutella M. Scheduling unrelated machines by randomized rounding. SIAM Journal on Discrete Mathematics, 2002, 15(4): 450-469 doi: 10.1137/S0895480199357078 [26] Tao J P. A better online algorithm for the parallel machine scheduling to minimize the total weighted completion time. Computers and Operations Research, 2014, 43: 215-224 doi: 10.1016/j.cor.2013.09.016 [27] Tao J P, Huang R, Liu T. A 2.28-competitive algorithm for online scheduling on identical machines. Journal of Industrial and Management Optimization, 2015, 11(1): 185-198 doi: 10.3934/jimo.2015.11.185 [28] Tao J P, Chao Z J, Xi Y G. A semi-online algorithm and its competitive analysis for a single machine scheduling problem with bounded processing times. Journal of Industrial and Management Optimization, 2010, 6(2): 269-282 doi: 10.3934/jimo.2010.6.269 [29] Tao J P, Chao Z J, Xi Y G, Tao Y. An optimal semi-online algorithm for a single machine scheduling problem with bounded processing time. Information Processing Letters, 2010, 110(8-9): 325-330 doi: 10.1016/j.ipl.2010.02.013 [30] Savelsbergh M W P, Uma R N, Wein J. An experimental study of lp-based approximation algorithms for scheduling problems. INFORMS Journal on Computing, 2005, 17(1): 123-136 doi: 10.1287/ijoc.1030.0055 [31] Gu H Y. Computation of approximate α-points for large scale single machine scheduling problem. Computers and Operations Research, 2008, 35(10): 3262-3275 doi: 10.1016/j.cor.2007.02.018 -






 下载:
下载: