-
摘要: 由于传统车辆跟驰建模预测方法无法遍历车辆所有可能的系统输入与运行状态的不确定性, 因而不足以从理论上保证对周边车辆安全跟驰行为预测的完整性与可信性. 为此提出车辆安全跟驰模式预测的形式化建模方法. 该方法利用随机可达集的遍历表现特征实现对周边车辆行为预测的不确定性表述, 并通过马尔科夫链逼近可达集的方式表达系统行为状态变化的随机性, 从而完成对周边车辆跟驰行为状态变化的精确概率预估. 为了表达跟驰情形中车辆之间的行为关联影响以及提高在线计算效率, 离线构建了关联车辆在状态及控制输入之间的安全关联矩阵, 描述周边车辆的安全跟驰控制输入选择规律, 并综合相关车辆的当前状态信息, 达到对周边车辆安全跟驰行为的在线分析与预估. 数值验证不仅表明提出的建模方法完备地表述了周边车辆所有的安全跟驰行为及过程, 显著提高了预测的精确度, 也论证了该方法对车辆跟驰控制策略建模分析与安全验证的有效性.Abstract: The traditional modeling methods of vehicle following are unable to traverse each possible control input and the uncertain motion states, which means that these methods are insufficient to ensure the integrity and reliability of prediction of the safe following behavior of surrounding vehicles in theory. Therefore, a formal modeling method based on reachability analysis and the representation of reachable sets is proposed to predict the safety vehicle following mode here. In this paper, the stochastic reachable set with ergodicity property is applied to characterize the uncertain prediction for the behavior of surrounding vehicle. Based on the discretization of the state and control input space of vehicle, the stochastic reachable sets of vehicles are abstracted to Markov chains that are used to express the random change of system states further. The accurate prediction probability of state change of vehicle can be achieved. In addition, a security incidence matrix of states and control inputs between correlated vehicles in following mode is structured offline. The offline simulations are helpful to improve the efficiency of online computing. The incidence matrix reflecting the correlation of vehicles approximately is applied to describe the rule of control input selection of surrounding vehicle under the safety following mode. Finally, the possible safe following behaviors of surrounding vehicle can be estimated and analyzed online by synthesizing the current states information of related vehicles, Markov chains and incidence matrix. The results of numerical verification show that the proposed modeling method formulates the whole set of safe following behaviors and process completely, and improves the accuracy of prediction significantly. Besides, the results also reveal that the method is effective to model, analysis and verify the security of following control strategy.
-
Key words:
- Vehicle following /
- formal modeling /
- stochastic reachable set /
- incidence relation
-
图 4 不同时间区段的跟驰车辆控制输入直方图
Fig. 4 Control input histograms of following vehicles for different time intervals
图 5 不同时间区段的跟驰车辆速度直方图
Fig. 5 Velocity histograms of following vehicles for different time intervals
表 1 离线运算中主要参数
Table 1 Main parameters used in offline operation
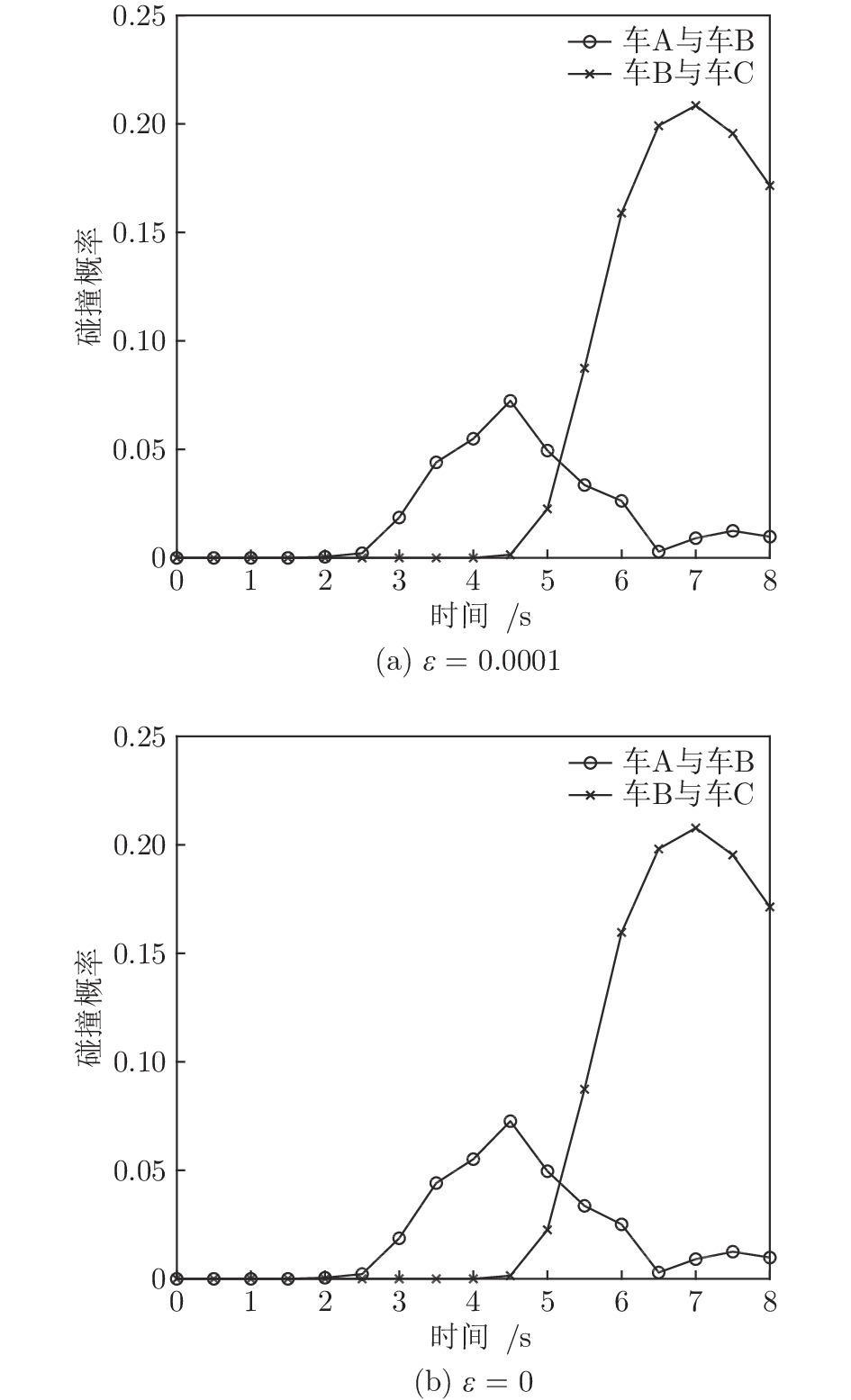
参数 赋值 $S / \mathrm{m}$ $[0,200]$ $V / \mathrm{(m/s)}$ $[0,20]$ $U$ $[-1,1]$ $n$ $40$ $m$ $10$ $g$ $6$ $\varpi$ $10$ $\varepsilon $ $0.000 1$ 
下载: 导出CSV
表 2 驾驶行为及车辆特性
Table 2 Driving behavior and vehicle characteristics
参数 赋值 $\gamma$ $0.2$ $\pmb \mu$ $[0.01\;0.04\;0.1\;0.4\;0.4\;0.05]$ $\pmb q_{(i,j)}(0)$ $[0\;0\;0\;1\;0\;0]$ $\tau / \mathrm{s}$ $0.5$ $\sigma$ $[1\;4\;8]$ $a^\mathrm{max} / \mathrm{(m/s^2)}$ $7$ $v^* \mathrm{(m/s)}$ $7.3$
下载: 导出CSV
表 3 初始属性-1: 均匀分布集合
Table 3 Initial state-1: Set with uniform distribution
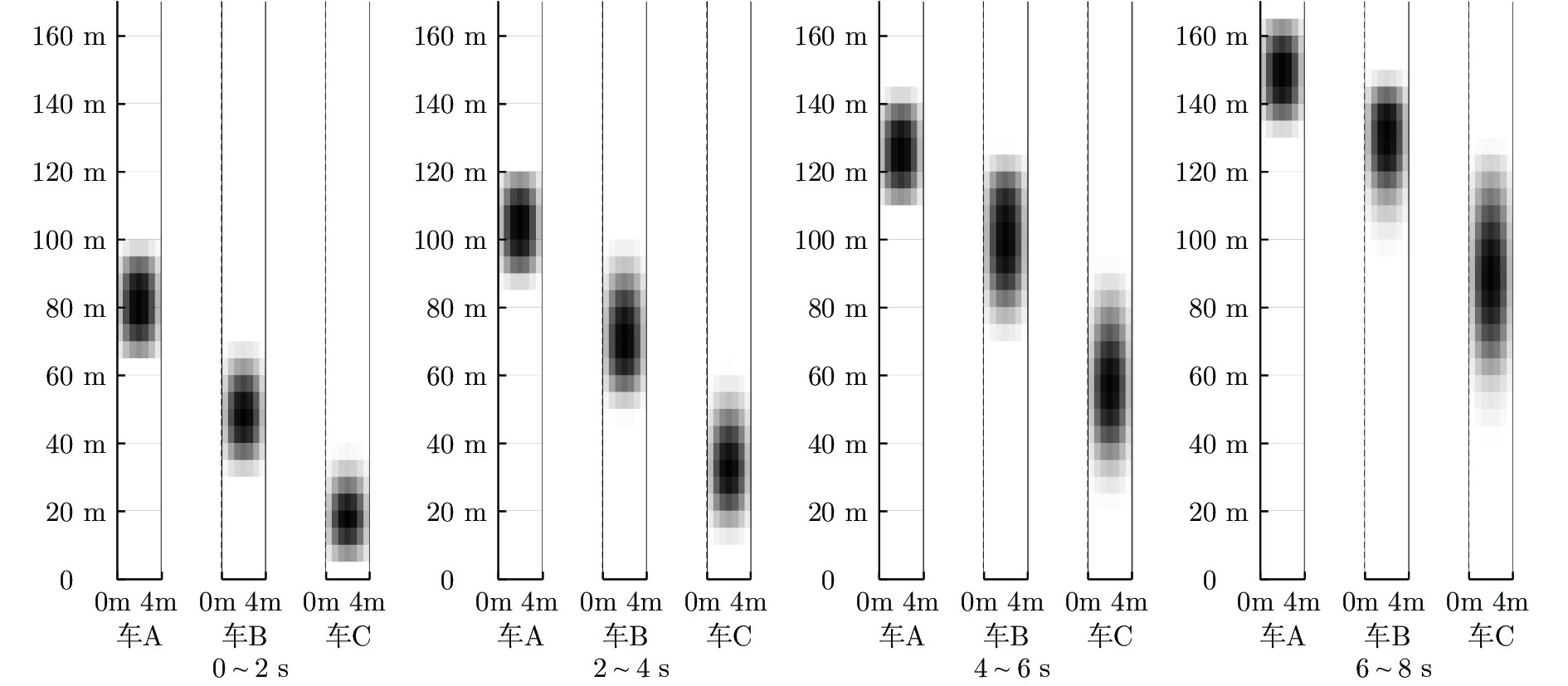
参数 赋值 $S^\mathrm{A}(0) / \mathrm{m}$ $[100,106]$ $V^\mathrm{A}(0) / \mathrm{(m/s)}$ $[2,4]$ $S^\mathrm{B}(0) / \mathrm{m}$ $[50,62]$ $V^\mathrm{B}(0) / \mathrm{(m/s)}$ $[8,10]$ $S^\mathrm{C}(0) / \mathrm{m}$ $[5,17]$ $V^\mathrm{C}(0) / \mathrm{(m/s)}$ $[12,14]$
下载: 导出CSV
表 4 初始属性-2: 均匀分布集合
Table 4 Initial state-2: Set with uniform distribution
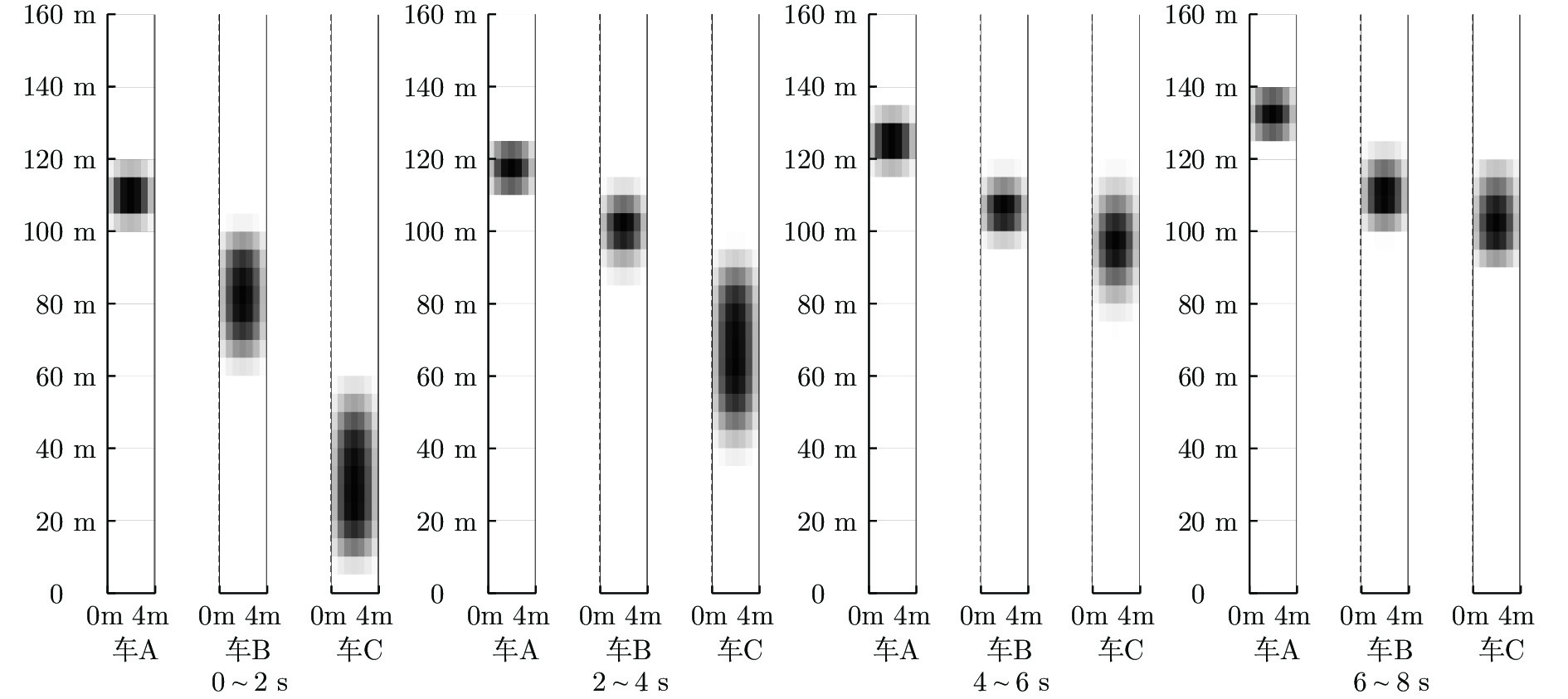
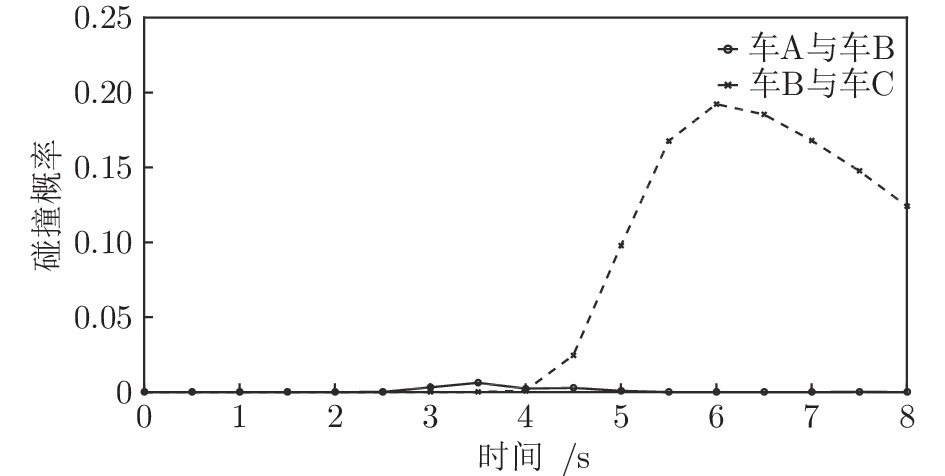
参数 赋值 $S^\mathrm{A}(0)\; / \mathrm{m}$ $[62, 74]$ $V^\mathrm{A}(0)\; / \mathrm{(m/s)}$ $[8, 10]]$ $S^\mathrm{B}(0)\; / \mathrm{m}$ $[25, 37]$ $V^\mathrm{B}(0)\; / \mathrm{(m/s)}$ $[6, 8]$ $S^\mathrm{C}(0)\; / \mathrm{m}$ $[5, 17]$ $V^\mathrm{C}(0)\; / \mathrm{(m/s)}$ $[2, 4]$
下载: 导出CSV
-
[1] 王殿海, 金盛. 车辆跟驰行为建模的回顾与展望. 中国公路学报, 2012, 25(1): 115−127 doi: 10.3969/j.issn.1001-7372.2012.01.018Wang Dian-Hai, Jin Sheng. Review and outlook of modeling of car following behavior. China Journal of Highway and Transport, 2012, 25(1): 115−127(in Chinese) doi: 10.3969/j.issn.1001-7372.2012.01.018 [2] Gazis D C, Herman R, Rothery R W. Nonlinear followthe-leader models of traffic flow. Operations Research, 1961, 9(4): 545−567 doi: 10.1287/opre.9.4.545 [3] Bando M, Hasebe K, Nakayama A, Shibata A, Sugiyama Y. Dynamical model of traffic congestion and numericalsimulation. Physical Review E, 1995, 51(2): 1035−1042 doi: 10.1103/PhysRevE.51.1035 [4] Helbing D, Tilch B. Generalized force model of traffic dynamics., Physical Review E, 1998, 58(1): 133−138 doi: 10.1103/PhysRevE.58.133 [5] Jiang R, Wu Q S, Zhu Z J. Full velocity difference model for a car-following theory. Physical Review E, 2001, 64(1): 7101−7104 [6] Wang Y, Zhang J, Lu G. Influence of driving behaviors on the stability in car Following. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(3): 1081−1098 doi: 10.1109/TITS.2018.2837740 [7] Xie D F, Zhao X M, He Z. Heterogeneous traffic mixing regular and connected vehicles: modeling and stabilization. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6): 2060−2071 doi: 10.1109/TITS.2018.2857465 [8] 李永福, 邬昌强, 朱浩, 唐晓铭. 考虑车辆跟驰作用和通信时延的网联车辆队列轨迹跟踪控制 [Online], 自动化学报, https://doi.org/10.16383/j.aas.c190046, 2019-12-04LI Yong-Fu, WU Chang-Qiang, ZHU Hao, Tang Xiao-Ming. Trajectory Tracking Control for Connected Vehicle Platoon Considering Car-following Interactions and Time Delays [Online], Acta Automatica Sinica, available: https://doi.org/10.16383/j.aas.c190046, December 4, 2019 [9] 李润梅, 张立威, 王剑. 基于时变间距和相对角度的无人车跟随控制方法研究. 自动化学报, 2018, 44(11): 2031−2040Li Run-Mei, Zhang Li-Wei, Wang Jian. A control method of unmanned car following under time-varying relative distance and angle. Acta Automatica Sinica, 2018, 44(11): 2031−2040 [10] Li X H, Yang T, Liu J, Qin X Q, Yu S W. Effects of vehicle gap changes on fuel economy and emission performance of the traffic flow in the ACC strategy. PLOS ONE, 2018, 13(7): e0200110 doi: 10.1371/journal.pone.0200110 [11] Kim T, Jeong H Y. A novel algorithm for crash detection under general road scenes using crash probabilities and an interactive multiple model particle filter. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2480−2490 doi: 10.1109/TITS.2014.2320447 [12] Asarin E, Dang T, Maler O. d/dt: A tool for reachability analysis of continuous and hybrid Systems. IFAC Proceedings Volumes, 2001, 34(6): 741−746 doi: 10.1016/S1474-6670(17)35267-9 [13] Bemporad A, Torrisi F D, Morari M. Optimization-based verification and stability characterization of Piecewise Affine and Hybrid Systems. In: Proceedings of Hybrid Systems: Computation and Control. Berlin, Germany: SpringerVerlag, 2000. 45−58 [14] Botchkarev O, Tripakis S. Verification of hybrid systems with linear differential inclusions using ellipsoidal approximations. In: Proceedings of Hybrid Systems: Computation and Control. Berlin, Germany: Springer-Verlag, 2000. 73−78 [15] Stursberg O, Krogh B H. Efficient representation and computation of reachable sets for hybrid systems. In: Proceedings of Hybrid Systems: Computation and Control. Berlin, Germany: Springer-Verlag, 2003. 482−497 [16] Girard A. Reachability of uncertain linear systems using zonotopes. In: Proceedings of Hybrid Systems: Computation and Control. Berlin, Germany: Springer-Verlag, 2005. 291−305 [17] Althoff M, Stursberg O, Buss M. Model-based probabilistic collision detection in autonomous driving. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2): 299−310 doi: 10.1109/TITS.2009.2018966 [18] Koschi M, Althoff M. SPOT: A tool for set-based prediction of traffic participants. In: Proceedings of the 2017 IEEE Intelligent Vehicles Symposium, Los Angeles, CA, USA, June 11-14, 2017. 1686−1693 [19] Althoff M, Lutz S. Automatic generation of safety-critical test scenarios for collision avoidance of road vehicles. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium, Changshu, Suzhou, China, June 26-30, 2018. 1326−1333 [20] Sontges S, Koschi M, Althoff M. Worst-case Analysis of the Time-To-React Using Reachable Sets. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium, Changshu, Suzhou, China, June 26-30, 2018. 1891−1897 [21] Eidehall A, Petersson L. Threat assessment for general road scenes using monte carlo sampling. IEEE Transactions on Intelligent Transportation Systems, 2006, 9(1): 137−147 -
图(9) / 表(4)
计量
- 文章访问数: 3123
- HTML全文浏览量: 2278
- PDF下载量: 305
- 被引次数: 0
