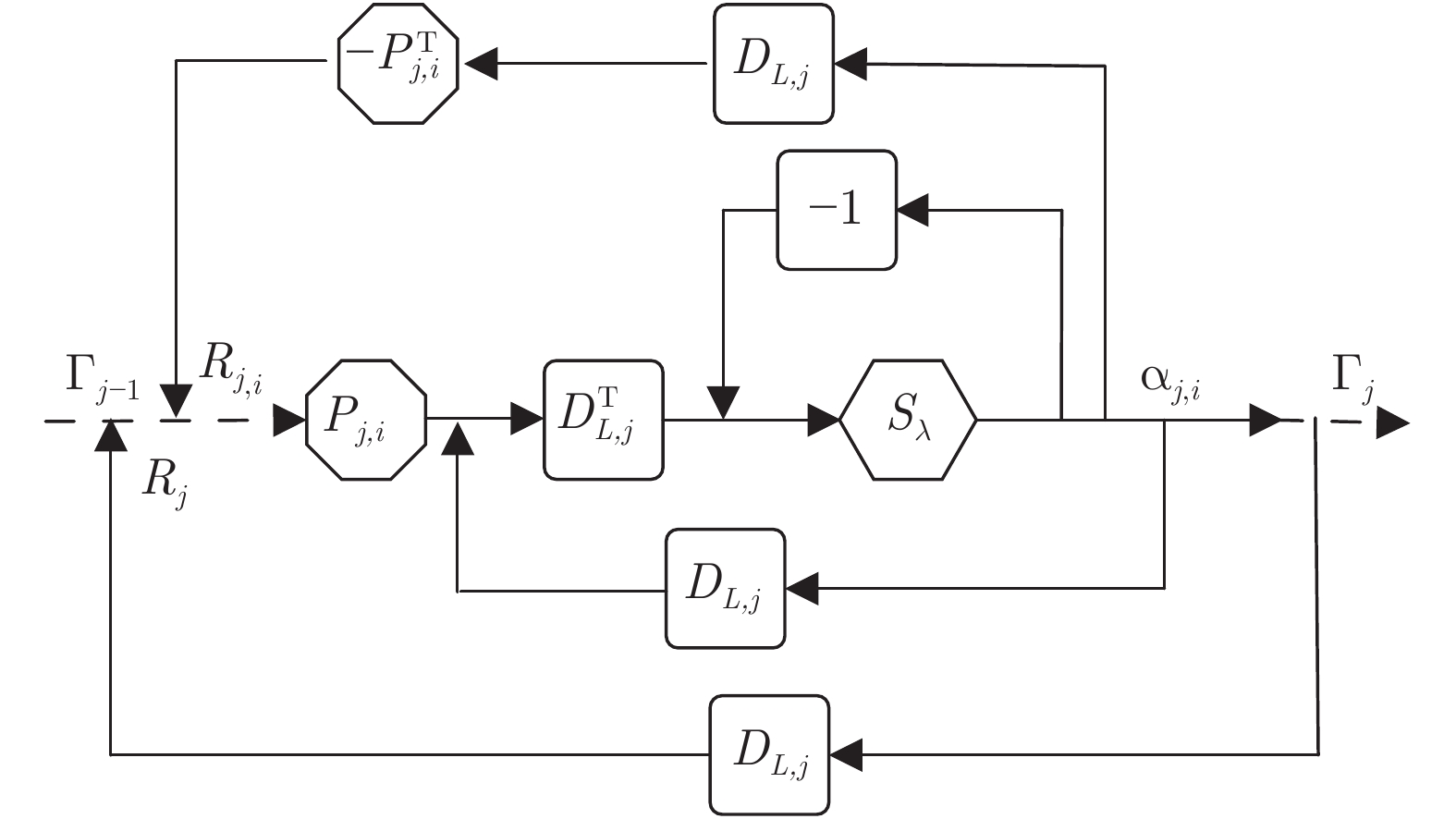
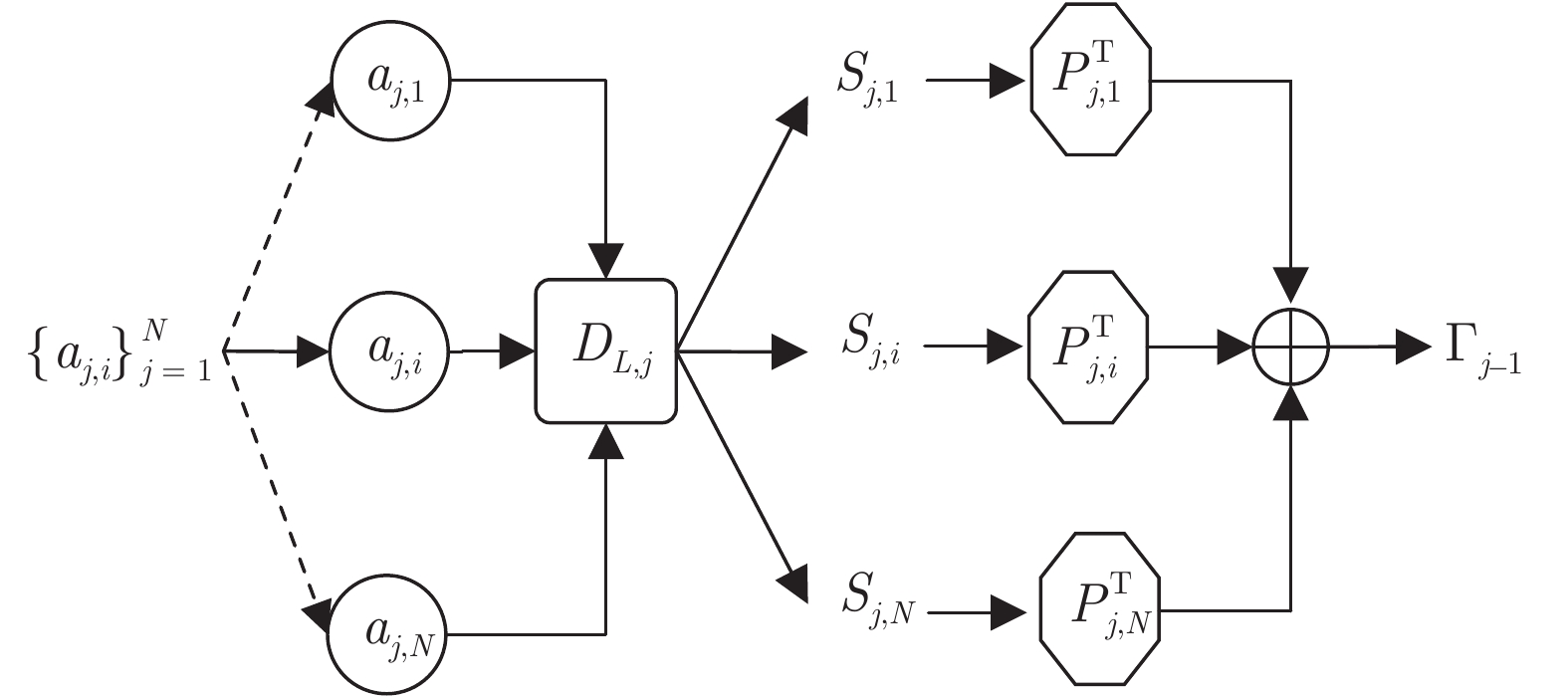
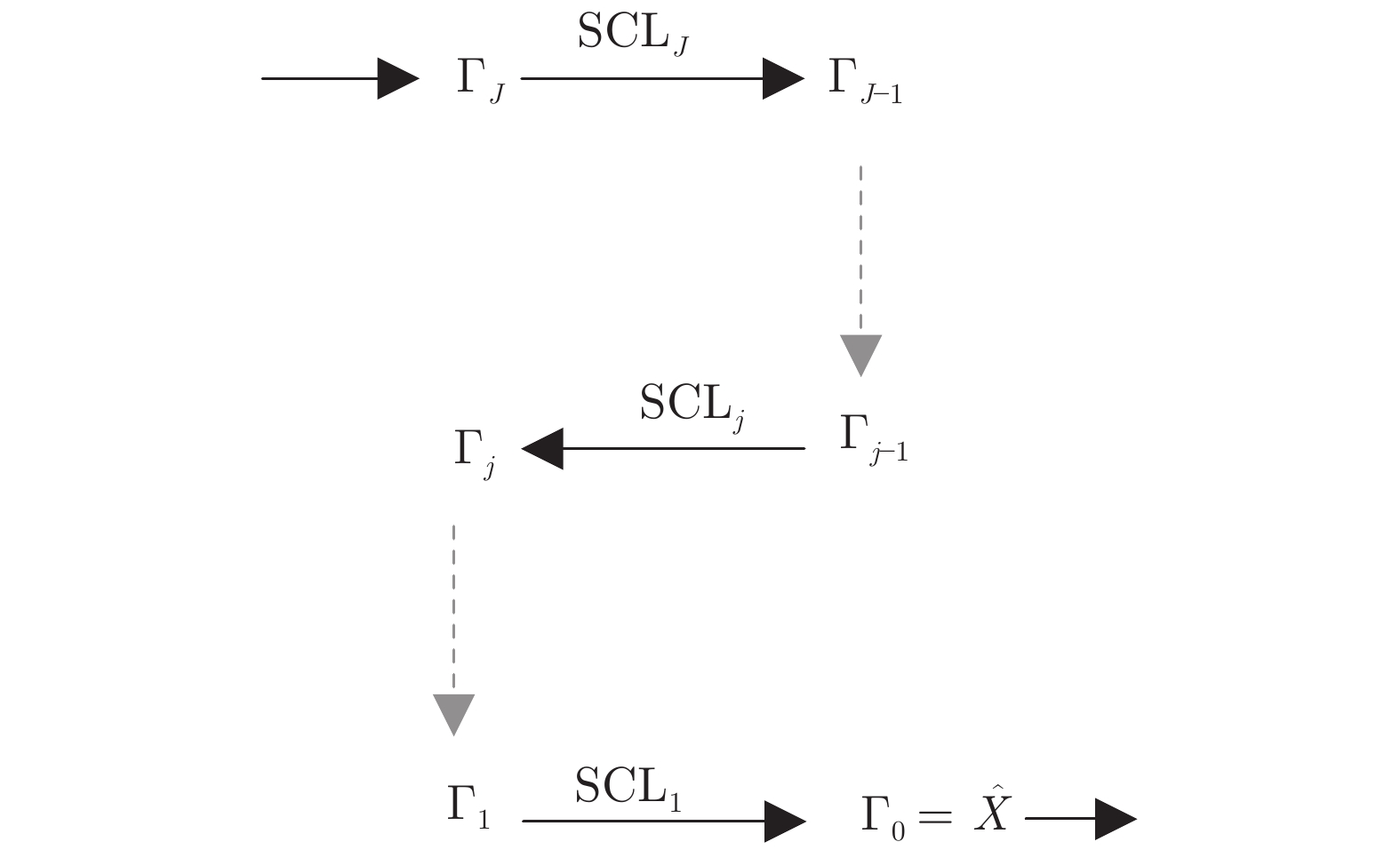
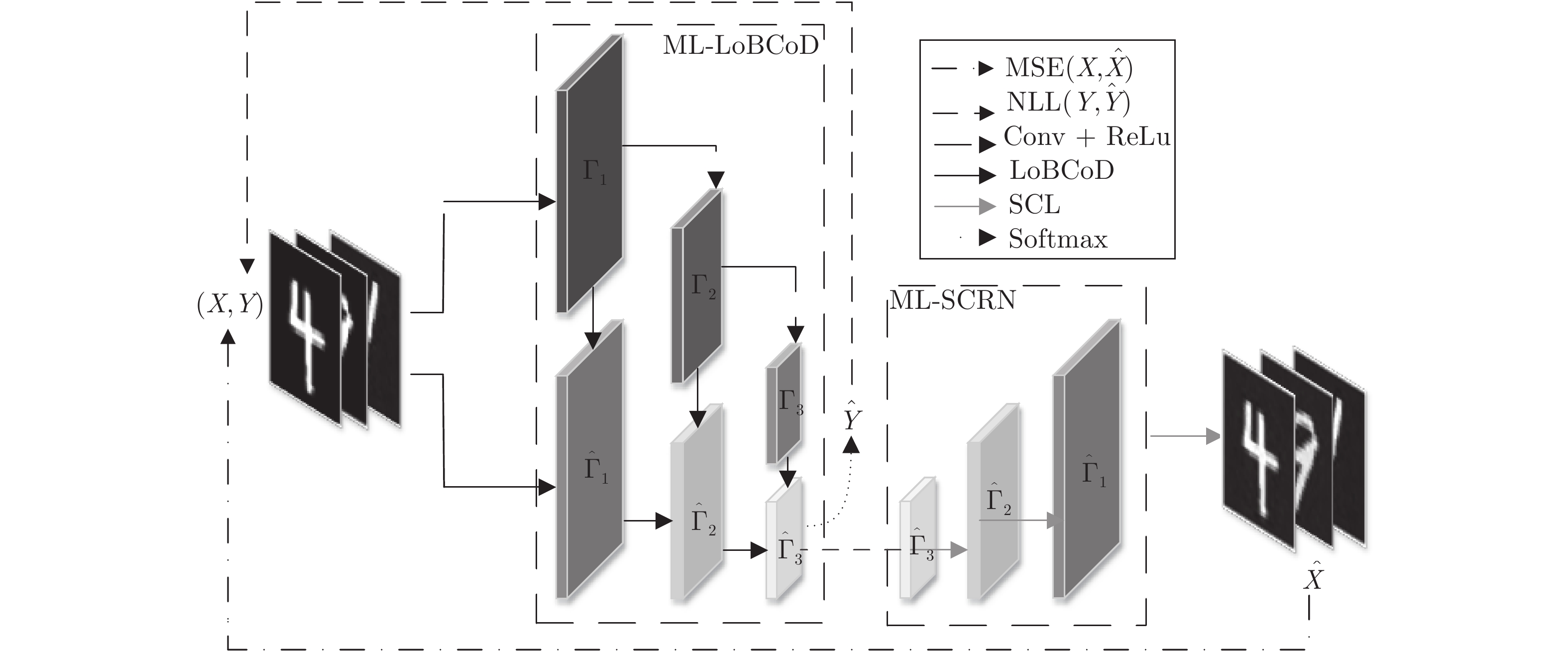
Multi-layer Local Block Coordinate Descent Algorithm and Unfolding Classification and Reconstruction Networks
-
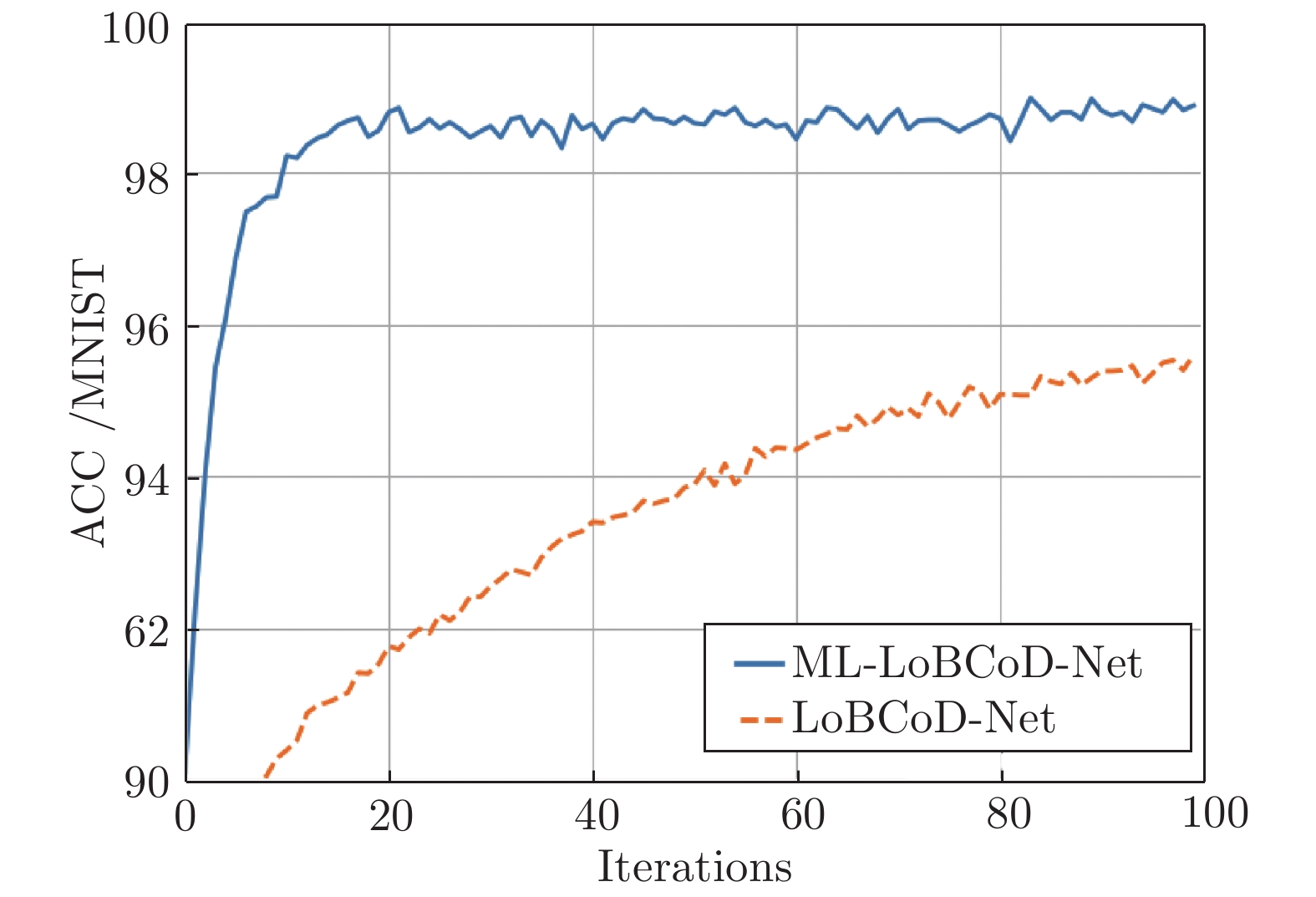
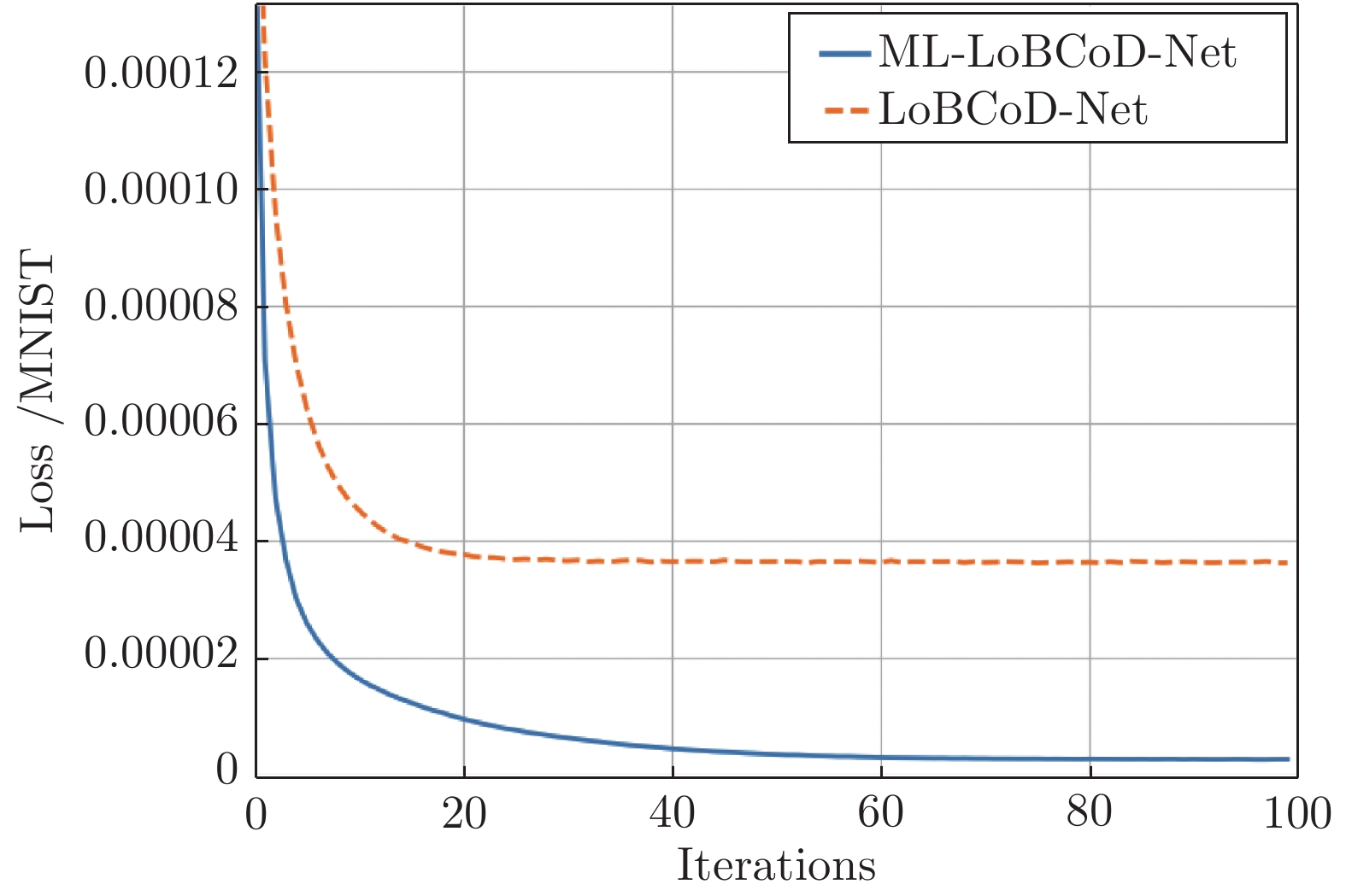
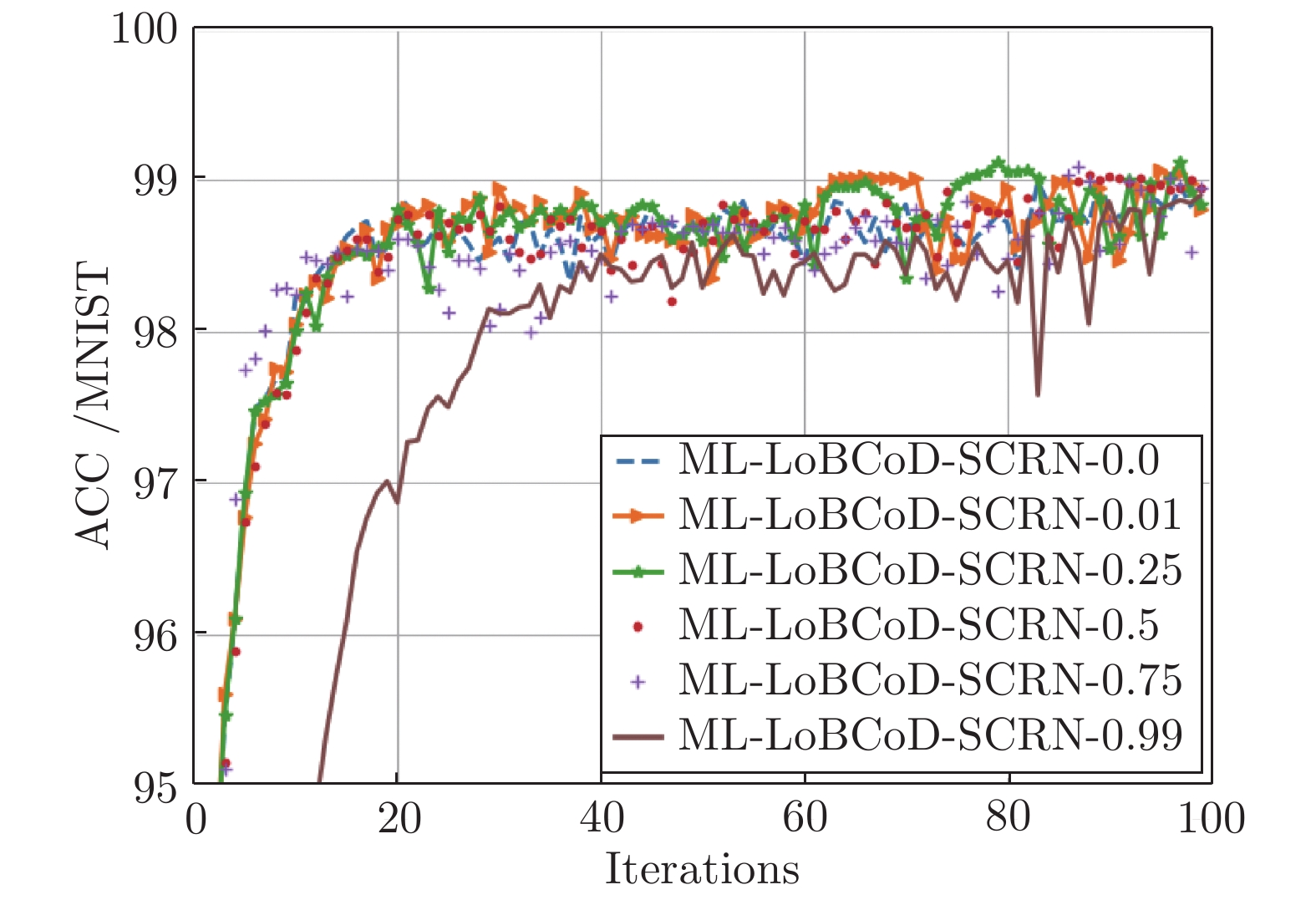
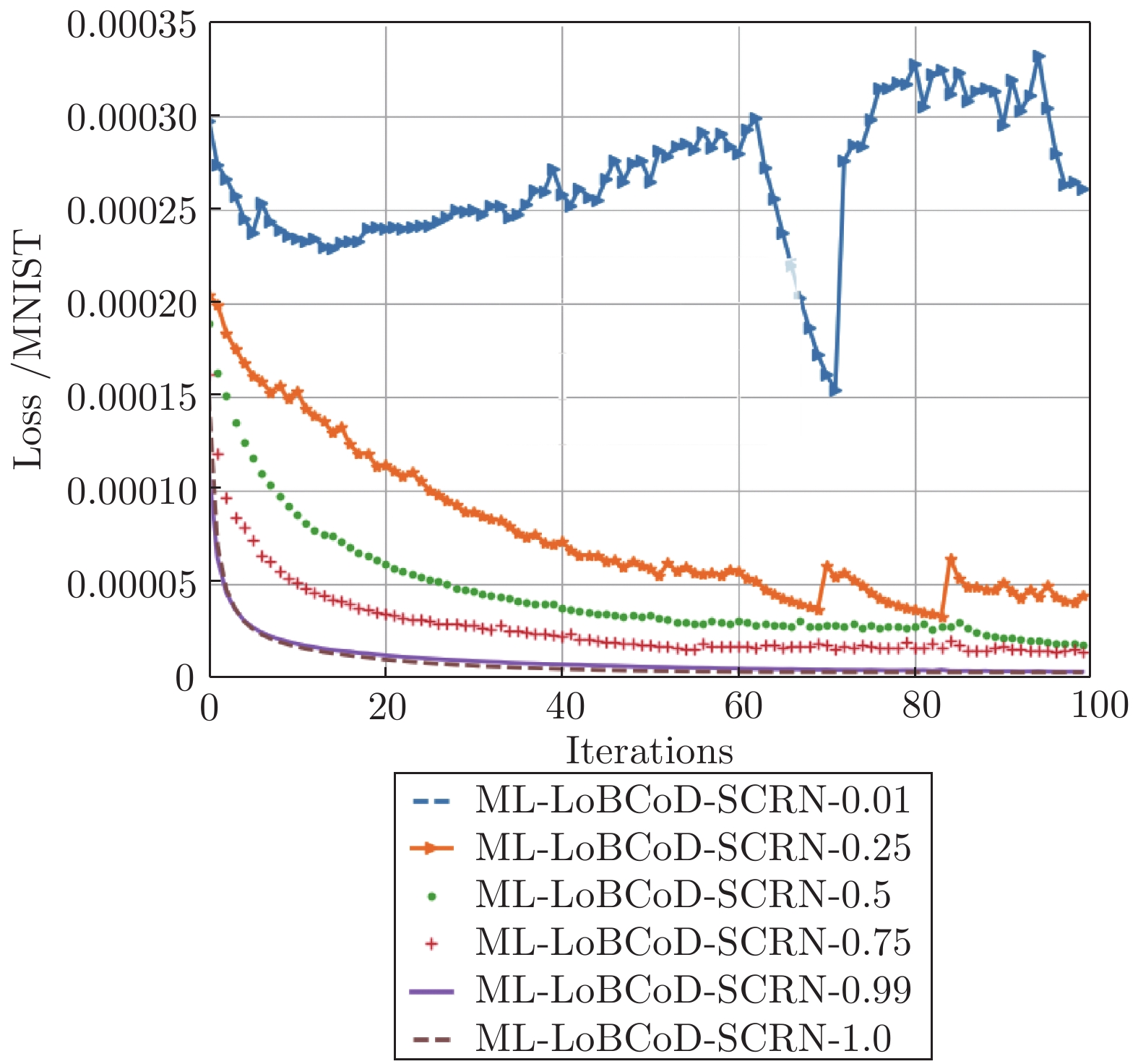
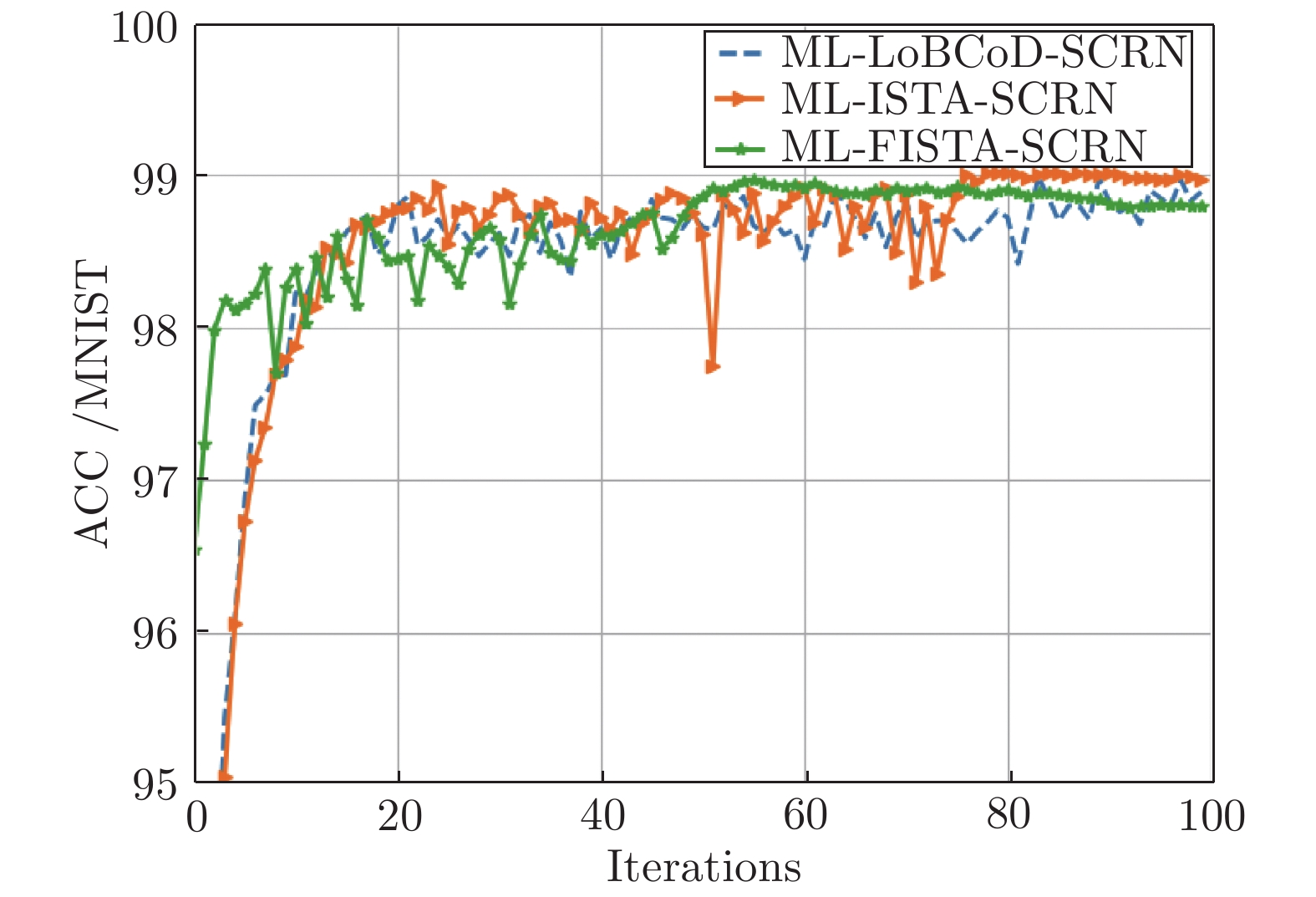
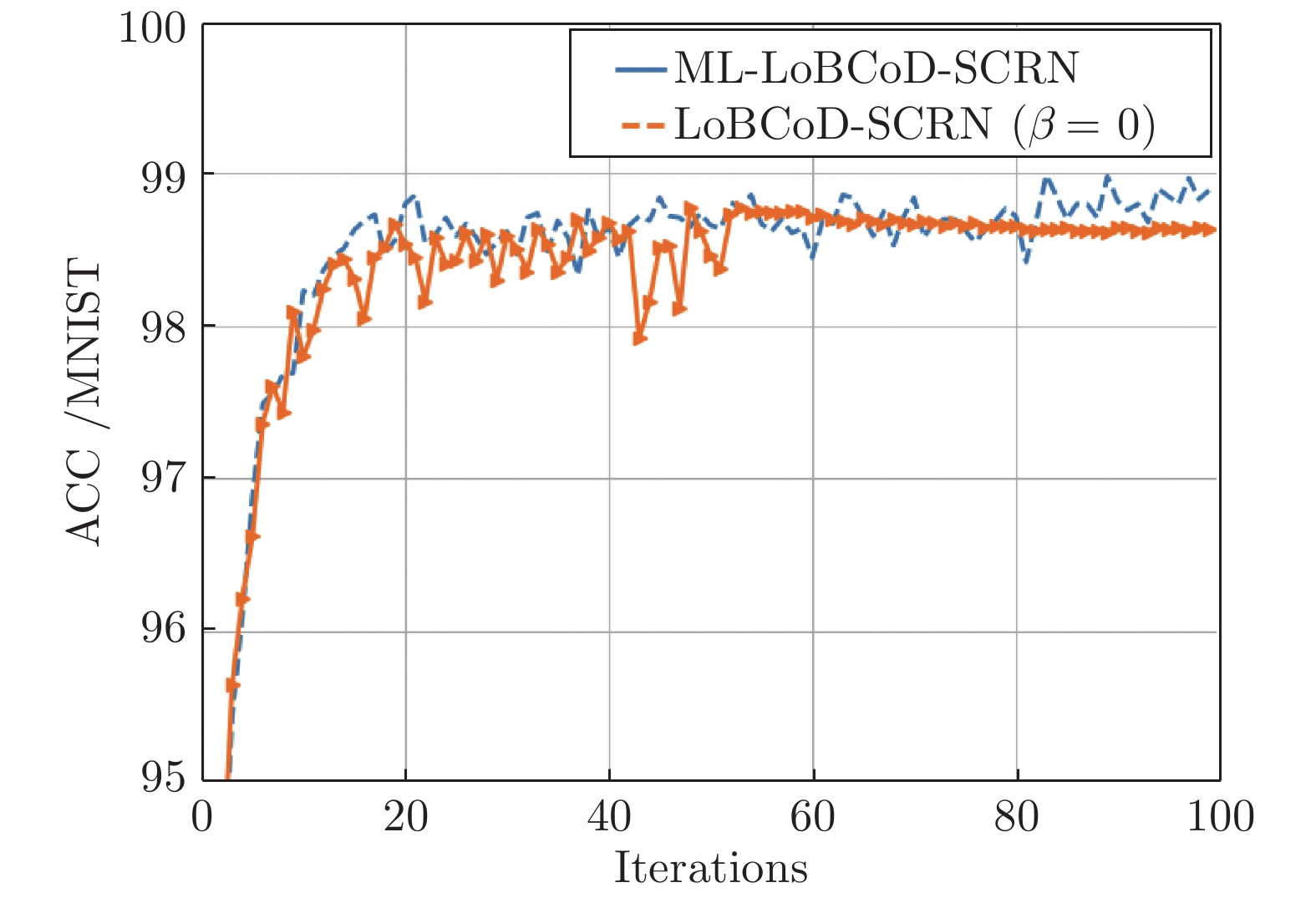
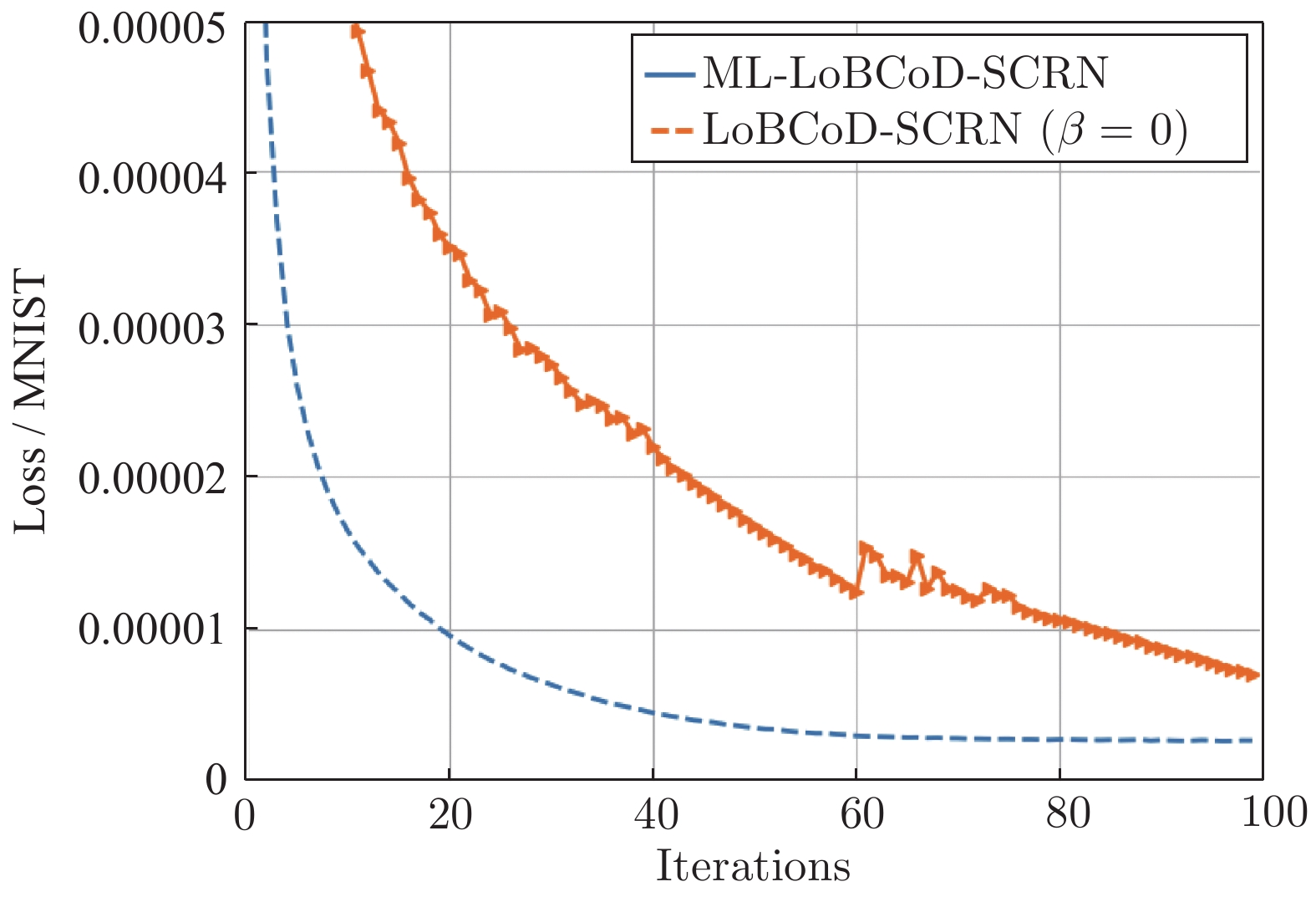
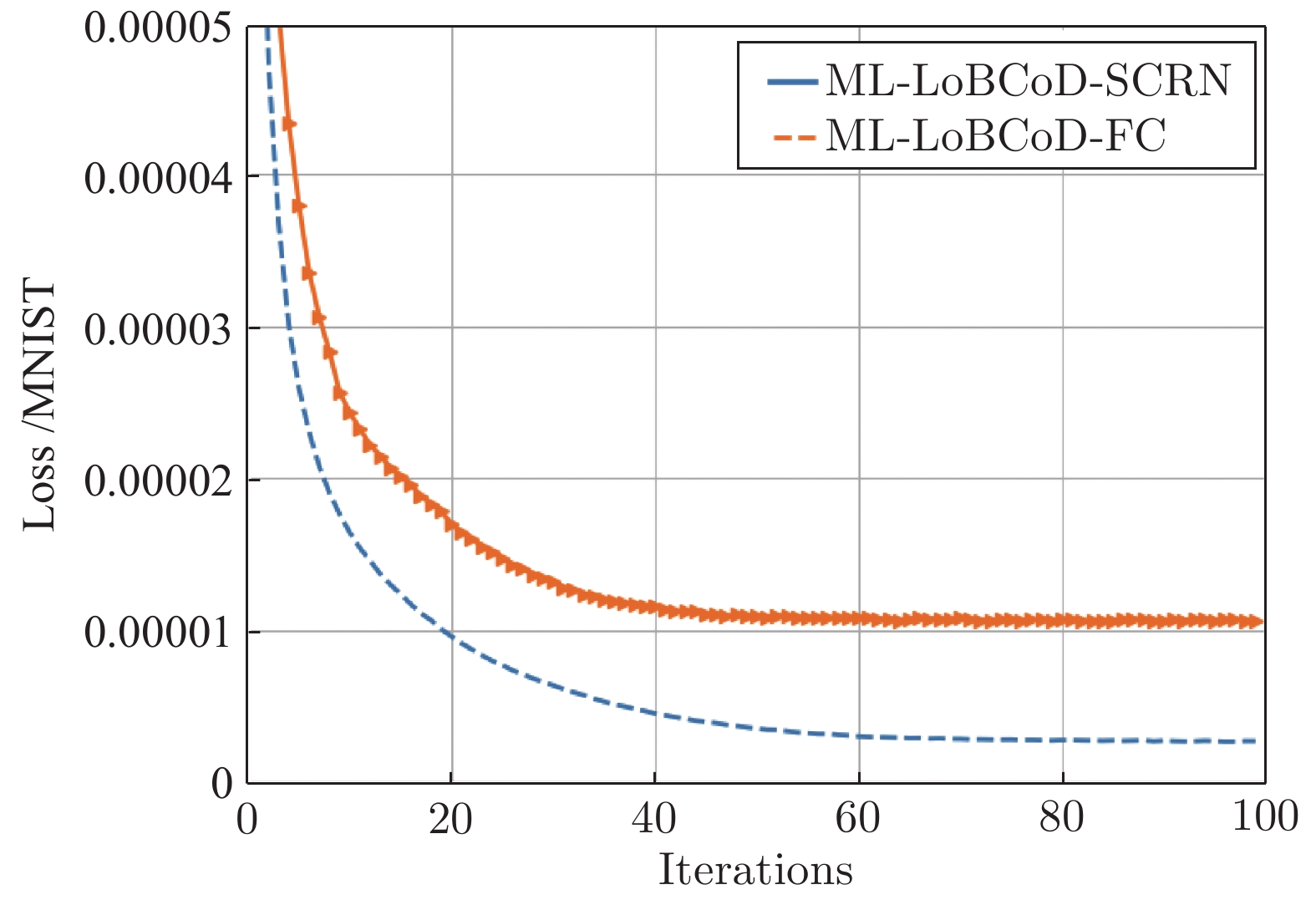
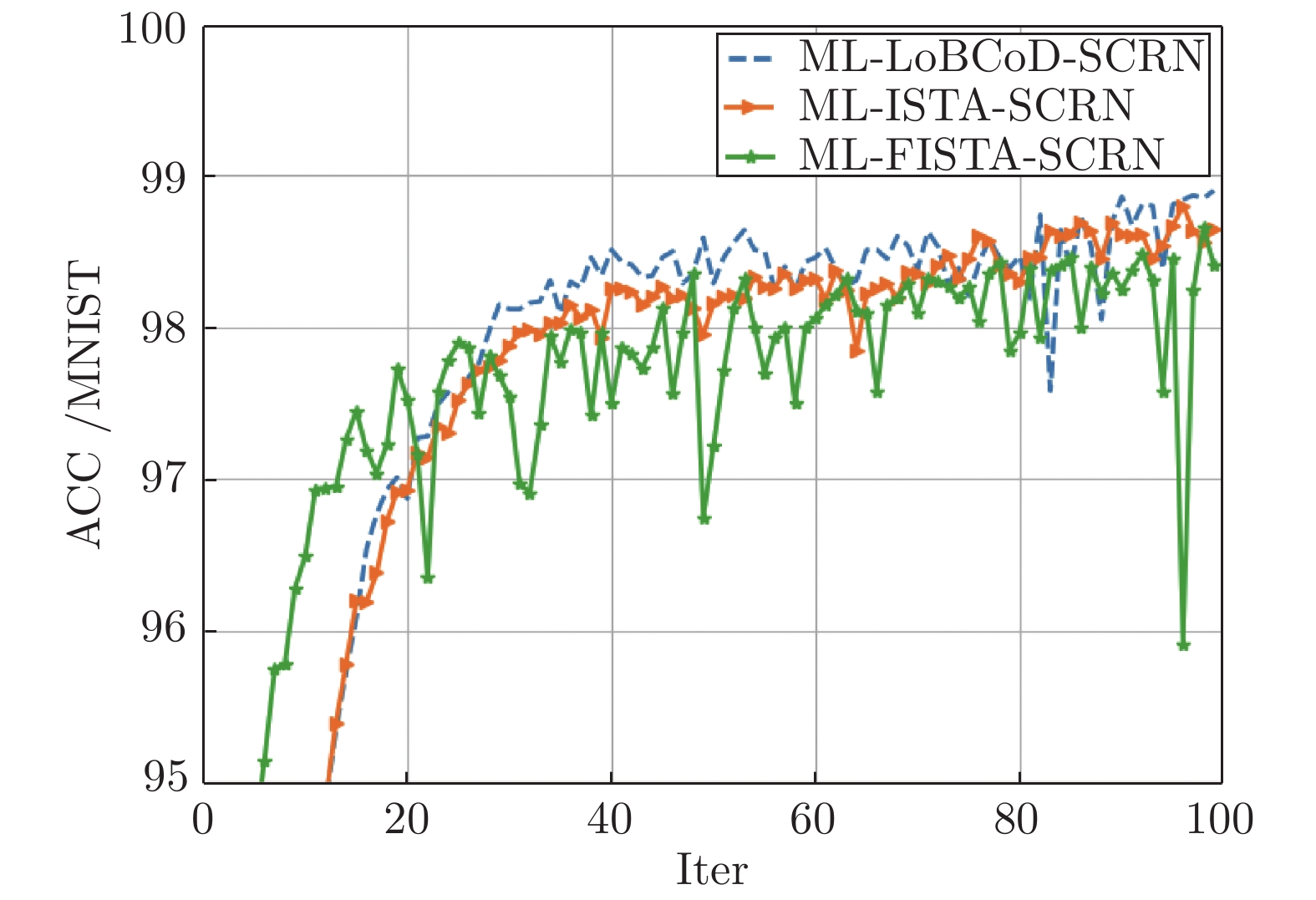
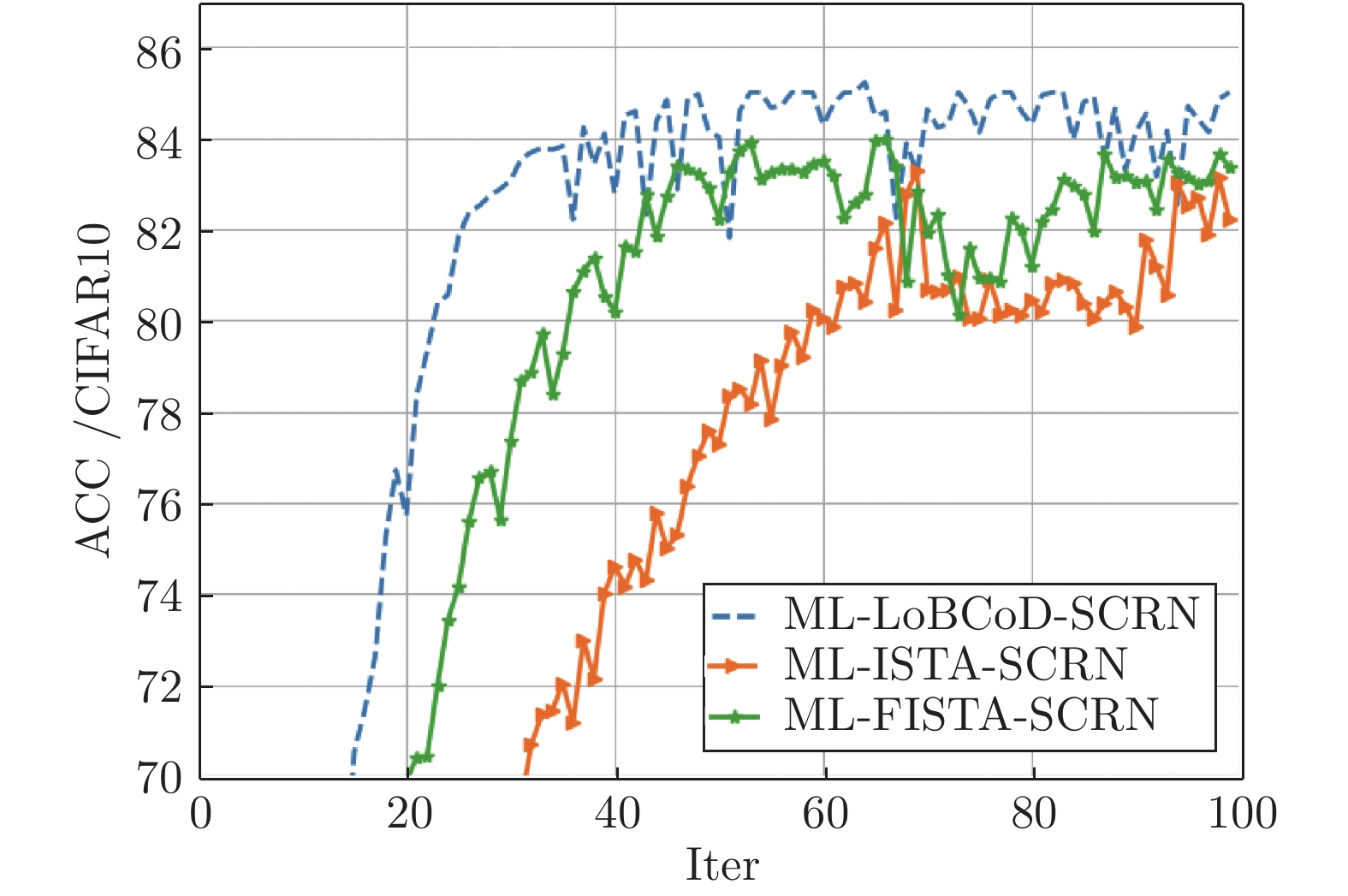
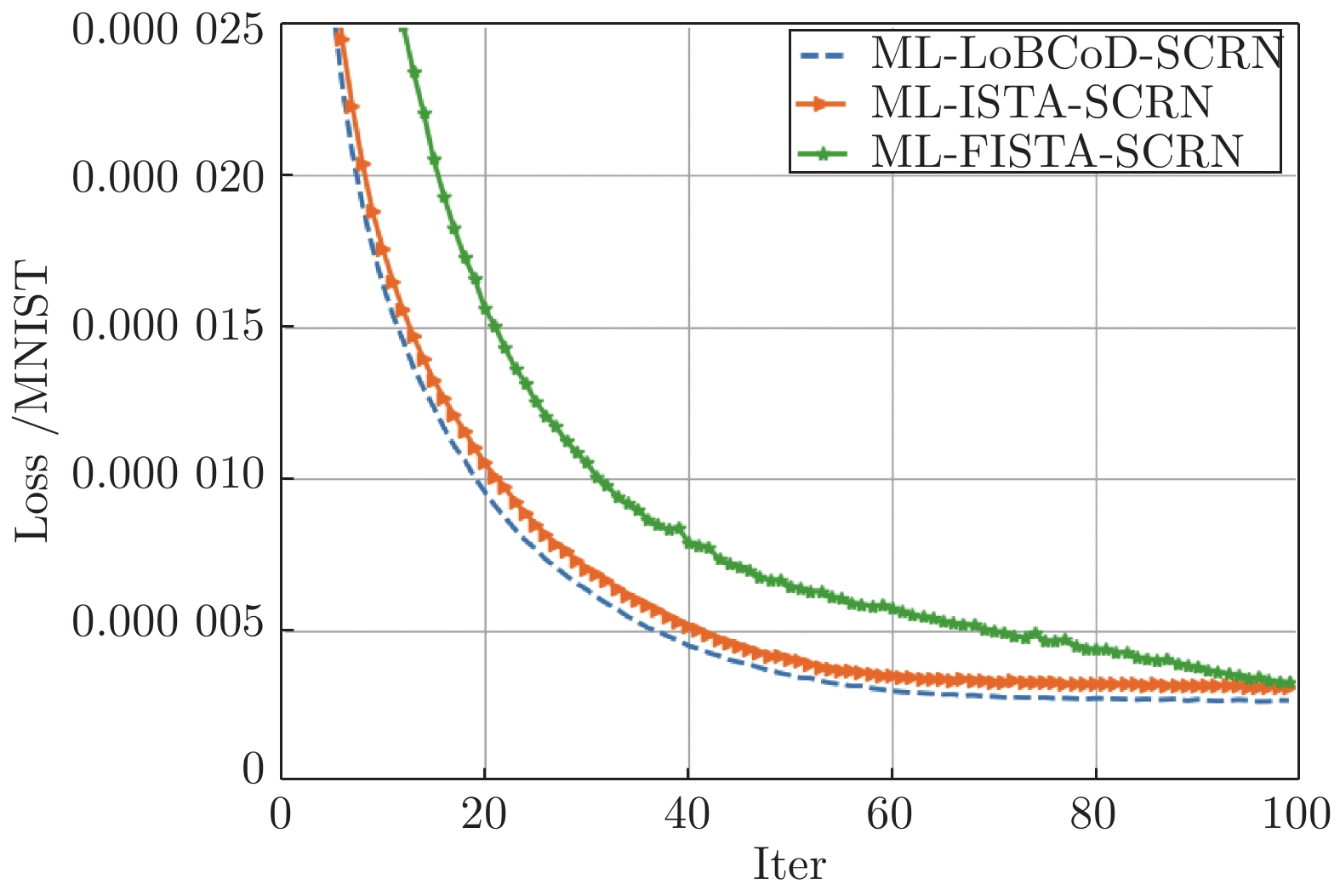
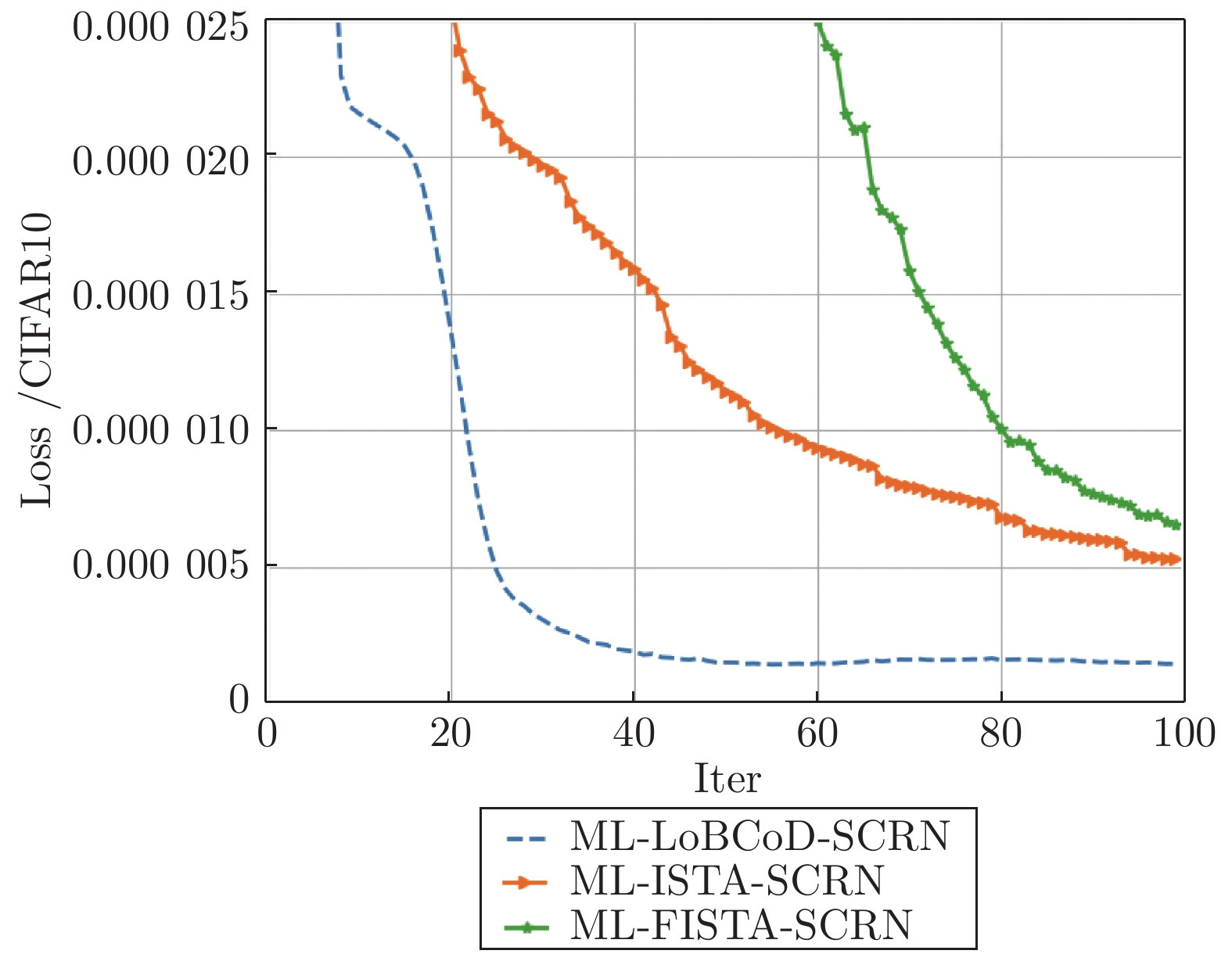
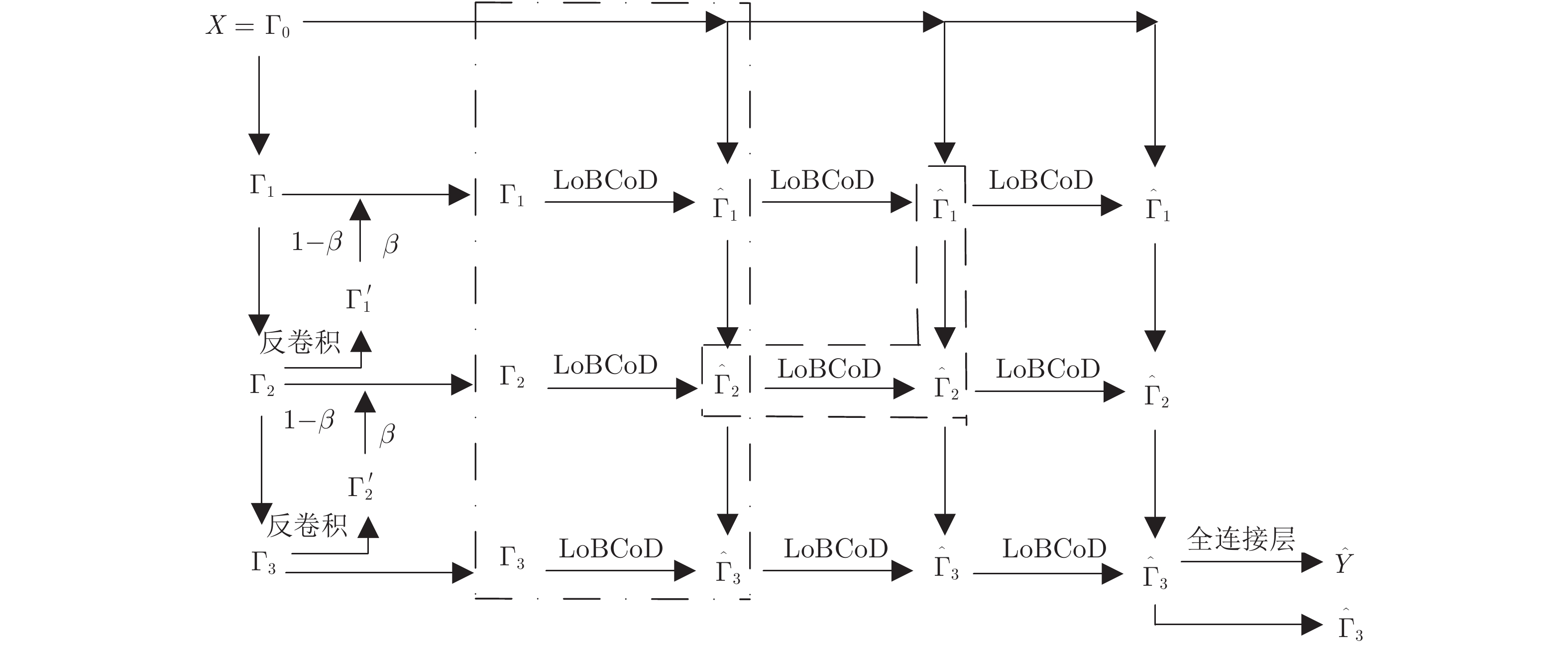
摘要: 卷积稀疏编码(Convolutional sparse coding, CSC)已广泛应用于信号或图像处理、重构和分类等任务中, 基于深度学习思想的多层卷积稀疏编码(Multi-layer convolutional sparse coding, ML-CSC)模型的多层基追踪(Multi-layer basic pursuit, ML-BP)问题和多层字典学习问题成为研究热点. 但基于傅里叶域的交替方向乘子法(Alternating direction multiplier method, ADMM)求解器和基于图像块(Patch)空间域思想的传统基追踪算法不能容易地扩展到多层情况. 在切片(Slice)局部处理思想的基础上, 本文提出了一种新的多层基追踪算法: 多层局部块坐标下降(Multi-layer local block coordinatedescent, ML-LoBCoD)算法. 在多层迭代软阈值算法(Multi-layer iterative soft threshold algorithm, ML-ISTA)和对应的迭代展开网络ML-ISTA-Net 的启发下, 提出了对应的迭代展开网络ML-LoBCoD-Net. ML-LoBCoD-Net实现信号的表征学习功能, 输出的最深层卷积稀疏编码用于分类. 此外, 为了获得更好的信号重构, 本文提出了一种新的多层切片卷积重构网络(Multi-layer slice convolutional reconstruction network, ML-SCRN), ML-SCRN实现从信号稀疏编码到信号重构. 我们对这两个网络分别进行实验验证. 然后将ML-LoBCoD-Net和ML-SCRN 进行级联得到ML-LoBCoD-SCRN合并网, 同时实现图像的分类和重构. 与传统基于全连接层对图像进行重建的方法相比, 本文提出的ML-LoBCoD-SCRN合并网所需参数少, 收敛速度快, 重构精度高. 本文将ML-ISTA和多层快速迭代软阈值算法(Multi-layer fast iterative soft threshold algorithm, ML-FISTA) 构建为ML-ISTA-SCRN和ML-FISTA-SCRN进行对比实验, 初步证明了所提出的ML-LoBCoD-SCRN分类重构网在MNIST、CIFAR10和CIFAR100数据集上是有效的, 分类准确率、损失函数和信号重构结果都优于ML-ISTA-SCRN和ML-FISTA-SCRN.
-
关键词:
- 多层卷积稀疏编码 /
- 多层基追踪 /
- 多层局部块坐标下降法 /
- 分类 /
- 重构
Abstract: Convolutional sparse coding (CSC) has been widely used in tasks such as signal or image processing, reconstruction, and classification. The multi-layer basic pursuit problem and the multi-layer dictionary learning problem of multi-layer convolutional sparse coding (ML-CSC) model based on deep learning idea have became research hotspots. But the alternating direction multiplier method (ADMM) solver based on Fourier domain and the traditional basic pursuit algorithm based on patch idea cannot be easily extended to multi-layer cases. Based on the idea of slice local processing, this paper proposes a new multi-layer basic pursuit algorithm: multi-layer local block coordinate descent (ML-LoBCoD) algorithm. Inspired by the multi-layer iterative soft threshold algorithm (ML-ISTA) and the ML-ISTA-Net, the corresponding iterative unfolding network ML-LoBCoD-Net is proposed. ML-LoBCoD-Net realizes the ability of learning signal representation, and the deepest convolutional sparse coding is used for classification. In addition, in order to obtain better signal reconstruction, a new multi-layer slice convolutional reconstruction network (ML-SCRN) is proposed. ML-SCRN implements the process from sparse coding to signal reconstruction. Experimental verification of the two networks are confirmed, respectively. Then ML-LoBCoD-Net and ML-SCRN are cascaded to obtain the classification and reconstruction network, ML-LoBCoD-SCRN, which realizes image classification and reconstruction at the same time. Compared with the reconstructing method based on the full connection layer, the proposed ML-LoBCoD-SCRN network requires fewer parameters, has faster convergence speed and higher reconstruction accuracy. In this paper, for comparative experiments, ML-ISTA-SCRN is constructed by ML-ISTA and ML-SCRN, and ML-FISTA-SCRN is constructed by the multi-layer fast iterative soft threshold algorithm (ML-FISTA) and ML-SCRN. The proposed ML-LoBCoD-SCRN is better than ML-ISTA-SCRN and ML-FISTA-SCRN on the classification accuracy rate, loss function value and signal reconstruction results for the MNIST, CIFAR10 and CIFAR100 datasets. -
表 1 几种分类网络在迭代100次时的分类准确率 (%)
Table 1 Classification accuracy of several classification networks at 100 iterations (%)
模型 ACC (MNIST) ACC (CIFAR10) CNN 98.74 79.00 ML-ISTA 99.11 82.93 ML-FISTA 99.16 82.79 ML-LISTA 98.80 82.68 LBP 99.19 80.73 ML-LoBCoD 99.15 85.53 表 2 两种分类重构网络在迭代100次对比
Table 2 Comparison of two classification reconstruction networks over 100 iterations
模型 ML-LoBCoD-SCRN ML-LoBCoD-FC 分类准确率ρ=0 (%) 99.15 98.91 重构误差 3.03×10−6 1.38×10−5 平均峰值信噪比 (dB) 30.77 22.79 时间 1 h 47 m 2 h 34 m 表 3 两种分类重构网络参数数量的比较
Table 3 Comparison of the parameters of two classification reconstruction networks
模型 ML-LoBCoD-SCRN ML-LoBCoD-FC 1st layer 6×6×1×64+64 6×6×1×64+64 2nd layer 6×6×64×128+128 6×6×64×128+128 3rd layer 4×4×128×512+512 4×4×128×512+512 4th layer 512×10+10 512×10+512×784+784 Total 1 352 330 1 753 818 表 4 三种网络在MNIST、CIFAR10和CIFAR100数据集下迭代100次各参数对比
Table 4 Comparison of the parameters of the three networks under the MNIST, CIFAR10 and CIFAR100 datasets 100 times
模型 分类准确率 (%) 重构误差 ( × 10−6 ) 运行时间 平均峰值信噪比 (dB) MNIST CIFAR10 CINAR100 MNIST CIFAR10 CINAR100 MNIST CIFAR10 CINAR100 MNIST CIFAR10 CINAR100 ML-LoBCoD-SCRN 98.90 84.40 83.41 3.03 1.44 3.14 1 h 47 m 1 h 12 m 0 h 57 m 30.77 32.46 29.97 ML-ISTA-SCRN 98.65 82.62 81.26 3.87 5.28 6.75 1 h 54 m 1 h 20 m 1 h 00 m 26.51 28.21 27.00 ML-FISTA-SCRN 98.41 83.48 80.34 3.42 6.52 8.95 1 h 56 m 1 h 25 m 1 h 05 m 29.75 27.63 25.14 -
[1] Aharon M, Elad M, and Bruckstein A, K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 2006, 54(11): 4311−4322 [2] Rey-Otero I, Sulam J, and Elad M. Variations on the convolutional sparse coding model. IEEE Transactions on Signal Processing, 2020, 68(1): 519−528 [3] Lecun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436−444 [4] Bristow H, Eriksson A, Lucey S. Fast convolutional sparse coding. In: Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, 2013, 391−398 [5] 陈善雄, 熊海灵, 廖剑伟, 周骏, 左俊森. 一种基于 CGLS 和 LSQR 的联合优化的匹配追踪算法. 自动化学报, 2018, 44(7): 1293−1303Chan Shan-Xiong, Xiong Hai-Ling, Liao Jian-Wei, Zhou Jun, Zuo Jun-Sen. A joint optimized matching tracking algorithm based on CGLS and LSQR. Acta Automatica Sinica, 2018, 44(7): 1293−1303 [6] Heide F, Heidrich W, Wetzstein G. Fast and flexible convolutional sparse coding. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, 2015, 5135−5143 [7] Papyan V, Romano Y, Sulam J, Elad M. Convolutional dictionary learning via local processing. In: Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV) , 2017, 5306–5314 [8] Zisselman E, Sulam J, Elad M. A local block coordinate descent algorithm for the CSC model. In: Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition, 2019, 8200−8209 [9] Papyan V, Romano Y, Elad M. Convolutional neural networks analyzed via convolutional sparse coding. The Journal of Machine Learning Research, 2017, 18(1): 2887−2938 [10] 张芳, 王萌, 肖志涛, 吴骏, 耿磊, 童军, 王雯. 基于全卷积神经网络与低秩稀疏分解的显著性检测. 自动化学报, 2019, 45(11):2148−2158Zhang Fang, Wang Meng, Xiao Zhi-Tao, Wu Jun, Geng Lei, Tong Jun, Wang Wen. Saliency detection based on full convolutional neural network and low rank sparse decomposition.Acta Automatica Sinica, 2019, 45(11): 2148−2158 [11] Sulam J, Papyan V, Romano Y, Elad M. Multi-layer convolutional sparse modeling: Pursuit and dictionary learning. IEEE Transactions on Signal Processing, 2018, 65(15): 4090−4104 [12] Sulam J, Aberdam A, Beck A, Elad M. On multi-layer basis pursuit, efficient algorithms and convolutional neural networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 1968−1980 [13] Aberdam A, Sulam J, Elad M. Multi-layer sparse coding: the holistic way. SIAM Journal on Mathematics of Data Science, 2019, 1(1): 46−77 [14] 常亮, 邓小明, 周明全, 武仲科, 袁野, 杨硕, 王宏安. 图像理解中的卷积神经网络. 自动化学报, 2016, 42(9): 1300−1312Chang Liang, Deng Xiao-Ming, Zhou Ming-Quan, Wu Zhong-Ke, Yuan Ye, Yang Shuo, Wang Hong-An. Convolution neural network in image understanding. Acta Automatica Sinica, 2016, 42(9): 1300−1312 [15] Badrinarayanan V, Kendall A, and Cipolla R. SegNet: a deep convolutional encoder-decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481−2495 [16] Elad P, Raja G. Matching pursuit based convolutional sparse coding. In: Proceedings of the 2018 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2018, 6847−6851. [17] Wohlberg B. Effificient algorithms for convolutional sparse representations. IEEE Transactions on Image Processing, 2016, 25(1): 301−315 [18] Sreter H, Giryes R. Learned convolutional sparse coding. In: Proceedings of the 2018 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2018, 2191−2195 [19] Liu J, Garcia-Cardona C, Wohlberg B, Yin W. First and second order methods for online convolutional dictionary learning. SIAM Journal on Imaging Sciences, 2018: 1589−1628 [20] Garcia-Cardona C, Wohlberg B. Convolutional dictionary learning: A comparative review and new algorithms. IEEE Transactions on Computational Imaging, 2018, 4(3): 366−381 [21] Peng G J. Joint and direct optimization for dictionary learning in convolutional sparse representation. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(2):559−573 [22] Papyan V, Sulam J, and Elad M. Working locally thinking globally: Theoretical guarantees for convolutional sparse coding. IEEE Transactions on Signal Processing, 2017, 65(21): 5687−5701 -




 下载:
下载: