-
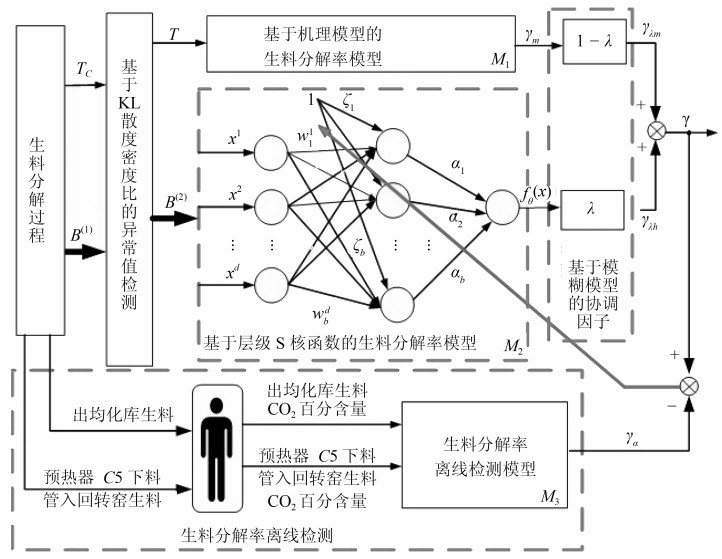
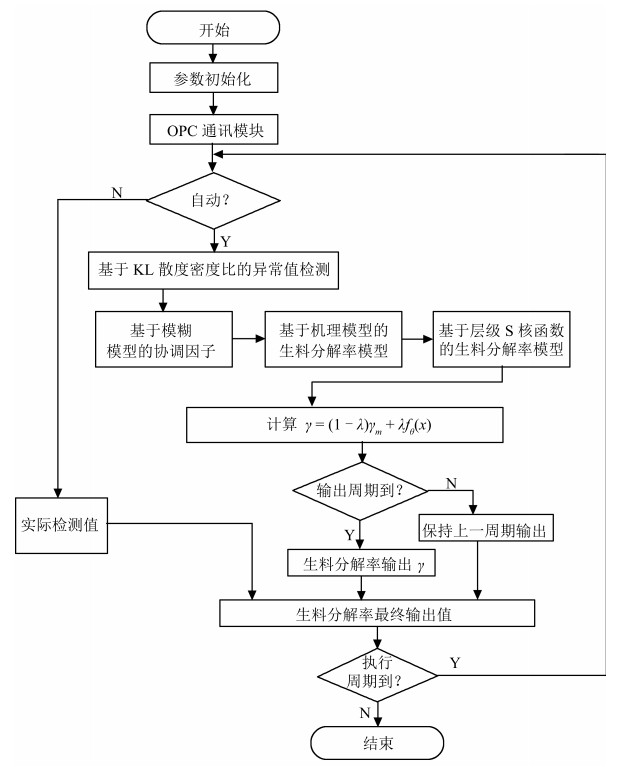
摘要: 水泥生料在分解炉内分解过程的质量指标是生料分解率(Raw meal decomposition ratio,RMDR),由于生料边界条件频繁变化且人工离线检测周期为2小时,致使产品质量指标合格率低且极易造成预热器C5下料管堵塞.为了解决上述问题,本文提出了基于数据与模型驱动的水泥生料分解率软测量模型,由基于Kullback-Leibler(KL)散度密度比的异常值检测、基于机理模型的生料分解率模型、基于层级Sigmoid(S)核函数的生料分解率模型、生料分解率离线检测模型和基于模糊模型的协调因子组成.实际应用结果表明,所提出的模型能够根据当前工况的变化选择正确的子模型,并且使生产远离故障工况.Abstract: The raw meal decomposition (RMDR) is a quality index in cement raw meal calcination process. The product quality index is low and it is easy to cause the preheater C5 feeding tube to be blocked because of varying boundary conditions and manual offline detection period of two hours. The product quality index is low and it is easy to cause the preheater C5 feeding tube to be blocked. To solve the above problem, a soft measurement model of raw meal decomposition ratio was proposed based on data and model. This model for raw meal calcination process consists of five modules, namely an outlier detection based on Kullback-Leibler (KL) divergence density ratio, a raw meal decomposition ratio model based on mechanism model, a raw meal decomposition ratio model based on hierarchical Sigmoid (S) kernel function, an offline detection model, and a coordination factor based on fuzzy model. The actual application results show that the model proposed can select right submodel according to current operating conditions, and is far from fault condition by the practical application results.1) 本文责任编委 王占山
-
变量 含义 变量 含义 
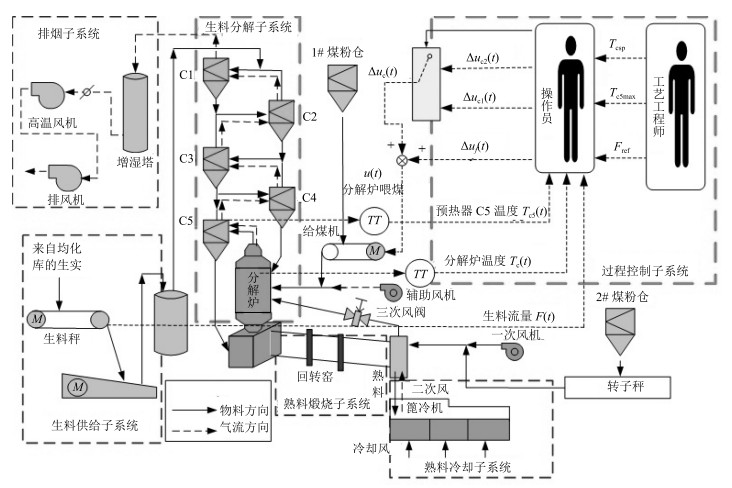
电机 ${\rm C}_i$ 第$i$个预热器 $F(t)$ 生料流量 $TT$ 温度传感器 C 控制器 $T_{\rm csp}$ 分解炉温度设定值 $T_{\rm c5\max}$ C5温度最大值 $F_{\rm ref}$ 生料流量参考值 $T_{\rm c} (t) $ 分解炉温度反馈 $T_{\rm c5} (t)$ 预热器${\rm C}$5温度反馈 $\Delta u_{\rm c1} (t)$ 控制器$T_{\rm c1}$输出 $\Delta u_{\rm c2} (t)$ 控制器$T_{\rm c2}$输出 $\Delta u_f (t)$ 控制器$FC$输出 $\gamma _a$ 分解率实际检测值 $\Delta u_{\rm c} (t)$ 控制器输出增量 $\Delta u(t)$ 控制器输出 变量 含义 变量 含义 $T_c (t) $ 分解炉温度反馈 $w_b^d$ 输入层与隐含层权值 $T(t)$ 分解炉温度滤波 $\zeta _b$ S核函数参数 $\lambda$ 协调因子 $B^{(1)}$ 输入变量集 $\gamma _m$ 模型输出值 $B^{(2)}$ 输入变量集滤波值 $f_\theta(x)$ 层级S函数输出 $\gamma _{\lambda m}$ 机理模型输出值 $M_1$ 机理模型 $\gamma _{\lambda h}$ 层级模型输出值 $M_2$ 层级模型 $\gamma _a$ 分解率实际检测值 $M_3$ 离线检测模型 $\gamma$ 分解率输出值 表 3 式(16)中参数的含义
Table 3 The meaning of variables in (16)
变量 含义 变量 含义 $k_0$ 反应速率常数 $E$ 反应活化能 $T$ 分解炉温度 $R$ 气体分子常数 表 4 本文所提方法与LS-SVM和RFMPCA-LS-SVM的RMSE对比
Table 4 The RMSE comparison among the method proposed and LS-SVM and RFMPCA-LS-SVM
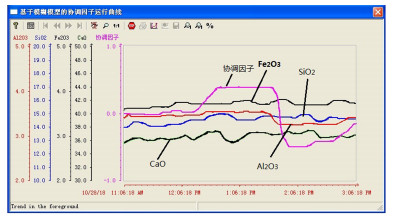
LS-SVM RFMPCA-LS-SVM 本文方法 RMSE 1.1326 1.0235 1.0198 表 5 基于模糊模型的协调因子参数选择
Table 5 Parameters selection based on fuzzy model
参数 值 参数 值 $\zeta _{{\text{Target}}}$ 5$\, \%$ $\zeta _{{\text{Tol}}}$ 15$\, \%$ $C_{\rm CaSP} (k)$ 36$\, \%$ $C_{\rm FeSP} (k)$ 3.4$\, \%$ $C_{\rm SiSP} (k)$ 13.5$\, \%$ $C_{\rm AlSP} (k)$ 3.55$\, \%$ $n_1$ 10 $n_2$ 5 $n_3$ 8 $n_4$ 5 $m$ 10 $l$ 1 表 6 生料中4种成分变化范围
Table 6 Range of four components in raw meal
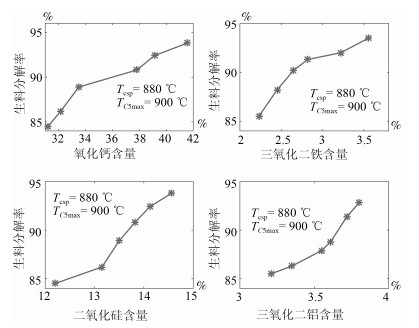
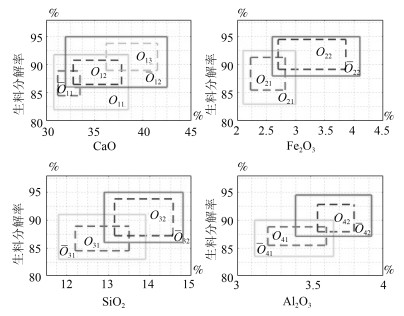
成分 含量($\%$) 成分 含量($\%$) CaO 35.5~36.3 ${\rm SiO_2}$ 14.5~14.9 ${\rm Fe_2O_3}$ 3.7~3.85 ${\rm Al_2O_3}$ 3.45~3.62 -
[1] 柴天佑.工业过程控制系统研究现状与发展方向.中国科学:信息科学, 2016, 46(8): 1003-1015 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgkx-fc201608005Chai Tian-You. Industrial process control systems: research status and development direction. Scientia Sinica Informationis, 2016, 46(8): 1003-1015 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgkx-fc201608005 [2] 柴天佑.复杂工业过程运行优化与反馈控制.自动化学报, 2013, 39(11): 1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtmlChai Tian-You. Operational optimization and feedback control for complex industrial processes. Acta Automatica Sinica, 2013, 39(11): 1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtml [3] 孙备, 张斌, 阳春华, 桂卫华.有色冶金净化过程建模与优化控制问题探讨.自动化学报, 2017, 43(6): 880-892 http://www.aas.net.cn/CN/abstract/abstract19067.shtmlSun Bei, Zhang Bin, Yang Chun-Hua, Gui Wei-Hua. Discussion on modeling and optimal control of nonferrous metallurgical purification process. Acta Automatica Sinica, 2017, 43(6): 880-892 http://www.aas.net.cn/CN/abstract/abstract19067.shtml [4] 范家璐, 张也伟, 柴天佑.一类工业过程运行反馈优化控制方法.自动化学报, 2015, 41(10): 1754-1761 http://www.aas.net.cn/CN/abstract/abstract18749.shtmlFan Jia-Lu, Zhang Ye-Wei, Chai Tian-You. Optimal operational oeedback control for a class of industrial process. Acta Automatica Sinica, 2015, 41(10): 1754-1761 http://www.aas.net.cn/CN/abstract/abstract18749.shtml [5] Qiao J H, Chai T Y. Intelligence-based temperature switching control for cement raw meal calcination process. IEEE Transactions on Control Systems Technology, 2015, 23(2): 644-661 doi: 10.1109/TCST.2014.2325896 [6] 乔景慧, 柴天佑.改进ELMAN网络的Q学习温度切换控制.控制理论与应用, 2015, 32(7): 955-962 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201507014Qiao Jing-Hui, Chai Tian-You. Temperature switching control integrated with improved ELMAN network and Q learning. Control Theory and Applications, 2015, 32(7): 955-962 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201507014 [7] 王君伟.新型干法水泥工艺生产计算手册.北京:化学工业出版社, 2013. 99-120Wang J W. New Dry Cement Production Process Calculation Manual. Beijing: Chemical Industry Press, 2013. 99-120 [8] Huang J L, Zhu Q S, Yang L J, Cheng D D, Wu Q W. A novel outlier cluster detection algorithm without top-n parameter. Knowledge-Based Systems, 2017, 121: 32-40 doi: 10.1016/j.knosys.2017.01.013 [9] 杉山将.图解机器学习.北京:人民邮电出版社, 2015. 137-142Sugiyama M. Machine Learning Using Diagrams. Beijing: Posts and Telecom Press, 2015. 137-142 [10] 杉山将.统计机器学习导论.北京:机械工业出版社, 2018. 464-468Sugiyama M. Introduction to Statistical Machine Learning. Beijing: China Machine Press, 2018. 464-468 [11] Wang W, Zhang B J, Wang D, Jiang Y, Qin S, Xue L. Anomaly detection based on probability density function with Kullback-Leibler divergence. Signal Processing, 2016, 126: 12-17 doi: 10.1016/j.sigpro.2016.01.008 [12] Qiao J H, Chai T Y. Soft measurement model and its application in raw meal calcination process. Journal of Process Control, 2012, 22: 344-351 doi: 10.1016/j.jprocont.2011.08.005 [13] Zhou X J, Wang D H, Shao Z G. 2-D regularized locality preserving projection algorithms for temporospatial feature reduction and its application in industrial data regression. Neurocomputing, 2015, 169: 373-382 doi: 10.1016/j.neucom.2014.08.088 [14] Witt P J, Sinnott M D, Cleary P W, Schwarz M P. Estimating a hierarchical simulation methodology for rotary kilns including granular flow and heat transfer. Minerals Engineering, 2018, 119: 244-262 doi: 10.1016/j.mineng.2018.01.035 [15] Koumboulis F N, Kouvakas N D. Indirect adaptive neural control for precalcination in cement plants. Mathematics and Computers in Simulation, 2002, 60 (5): 325-334 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3a2b021b5e68f0d9e495c2712a45857d [16] Fellaou S, Harnoune A, Seghra M A, Bounahmidi T. Statistical modeling and optimization of the combustion efficiency in cement kiln precalciner. Energy, 2018, 115: 351-359 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cfab5b848d5c81f318dbdeb8f3bd63ea [17] 谢克平, 水泥新型干法生产精细化操作与管理.北京:化学工业出版社, 2007. 130-161Xie Ke-Ping. Refined Operation and Management of Cement New Dry Process. Beijing: Chemical Industry Press, 2007. 130-161 [18] Qiao J H, Chai T Y, Wang H. Intelligent setting control for clinker calcination process. Asian Journal of Control, 2014, 16: 243-263 doi: 10.1002/asjc.668 [19] Nguyen X, Wainwright M J, Jordan M I. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Transactions on Information Theory, 2010, 56: 5847-5861 doi: 10.1109/TIT.2010.2068870 [20] Qiao J H, Chai T Y. Quality index modeling based on mechanism and multirate sampled-data in cement raw meal calcination process. In: Proceedings of the 27th Chinese Control and Decision Conference (CCDC2015), Qingdao, China: IEEE, 2015. 23-25 [21] Masashi S. Introduction to Statistical Machine Learning. Beijing: China Machine Press, 2018. 239-244 [22] Qiao J H, Chai T Y. RMDR optimal setting based on multi-model for raw meal calcinations process. In: Proceedings of the 36th Chinese Control Conference (CCC2017), Dalian, China: IEEE, 2017. 4494-4499 [23] Fábio B G, Silvia M N, Renato F, Horacio S. A text summarization method based on fuzzy rules and applicable to automated assessment. Expert Systems with Applications, 2019, 115: 264-275 doi: 10.1016/j.eswa.2018.07.047 -




 下载:
下载: