Hybrid Discrete Teaching-learning-based Optimization Algorithm for Solving Complex Parallel Machine Scheduling Problem
-
摘要: 针对制造行业中广泛存在的一类复杂并行机调度问题, 即带到达时间、多工序、加工约束和序相关设置时间的并行机调度问题(Parallel machine scheduling problem with arrival time, multiple operations, process restraints and sequence-dependent setup times, PMSP_AMPS), 建立问题的排序模型并提出一种混合离散教与学优化算法进行求解, 优化目标为最小化最大完工时间.首先, 根据标准教与学算法(Teaching-learning-based optimization, TLBO)中两阶段个体更新公式的特点, 在保留每一阶段个体更新公式框架不变的前提下, 对公式中具体改变实数个体或向量的每个核心操作均用所设计的排列操作进行替换, 使其可直接在离散问题解空间中执行基于标准教与学算法机理的全局搜索, 从而明显提高了原算法的全局搜索效率.其次, 采用交换操作和插入操作构造了一种简洁有效地变邻域局部搜索, 对全局搜索发现的优质解区域进行细致搜索, 从而进一步增强了算法的性能.通过对不同测试问题的仿真实验和算法比较, 验证了所提算法可有效求解PMSP_AMPS.Abstract: This paper proposes a hybrid discrete teaching-learning-based optimization algorithm and set up the scheduling model for solving the parallel machine scheduling problem with arrival time, multiple operations, process restraints, and sequence-dependent setup times (PMSP_AMPS), which widely exists in the manufacturing process. The criterion is to minimize the maximum completion time. Firstly, according to the characteristics of the two stage individual updating formulas in the standard teaching-learning-based optimization (TLBO) algorithm, under the premise of keeping the framework of individual updating formulas at each stage unchanged, each core operation that specifically changes the real number or vector in the formula is replaced with proposed arrangement operation, so that it can execute the global search directly in the discrete solution space based on the TLBO mechanism, which significantly improve the TLBO's global exploration ability. Secondly, a simple but effective variable-neighborhood local search is constructed by using interchange and insert operations, which can perform a detailed search of the high-quality solution regions found by the global search, thereby further enhancing the performance of the algorithm. Simulation experiments and comparisons on different instances demonstrate that the proposed algorithm can effectively solve PMSP_AMPS.
-
Key words:
- Parallel machine scheduling problem (PMSP) /
- multiple operations /
- sequence-dependent setup times /
- arrival times /
- discrete teaching-learning-based optimization
1) 本文责任编委 阳春华 -
图 1 工序为$ \pi $ = [1 3 2 5 4 1 3 1 3 4]时的甘特图
Fig. 1 The Gantt chart of $ \pi $ = [1 3 2 5 4 1 3 1 3 4]
图 6 各算法在不同时间参数下的均值线及95 %置信度下Tukey$'$s HSD检验的置信区间
Fig. 6 Means plot and 95 % Tukey$'$s HSD confidence intervals for the interaction between the algorithms and the different time factor $ \rho $
图 7 各算法在不同时间参数下的均值线及95 %置信度下Tukey$'$s HSD检验的置信区间
Fig. 7 Means plot and 95 % Tukey$'$s HSD confidence intervals for the interaction between the algorithms and the different time factor $ \rho $
表 1 工序加工约束、序相关设置时间和工件到达时间表($ \pi $ = [1 3 2 5 4 1 3 1 3 4])
Table 1 The schedule of process constraint, sequence setup time and arrival time ($ \pi $ = [1 3 2 5 4 1 3 1 3 4])
可执行操作的设备 序相关设置时间 首次到达设备的时间 操作1 操作2 操作3 工件1 工件2 工件3 工件4 工件5 m1 m2 m3 工件1 m1/m2 m1/m2/m3 m1/m3 — 83 38 39 47 35 34 23 工件2 m1 — — 53 — 66 45 25 38 78 98 工件3 m3 m2/m3 m2 64 57 — 72 46 52 23 32 工件4 m1/m3 m1 — 46 67 83 — 55 132 131 98 工件5 m1/m3 — — 40 66 83 77 — 114 99 112 
下载: 导出CSV
表 2 工件加工时间表($ \pi $ = [1 3 2 5 4 1 3 1 3 4]) ($t$/s)
Table 2 The processing time table ($ \pi $ = [1 3 2 5 4 1 3 1 3 4]) ($t$/s)
操作1 操作2 操作3 m1 m2 m3 m1 m2 m3 m1 m2 m3 工件1 62 44 — 78 86 26 48 — 87 工件2 41 — — — — — — — — 工件3 — — 31 — 58 65 — 42 — 工件4 32 — 31 27 — — — — — 工件5 74 — 36 — — — — — —
下载: 导出CSV
表 3 参数水平设置表
Table 3 Combinations of parameter values
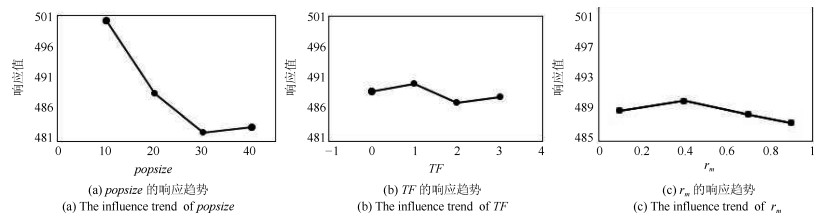
参数 水平 1 2 3 4 $ popsize $ 10 20 30 40 $ TF $ 0 1 2 3 $ r_{m} $ 0.1 0.4 0.7 0.9
下载: 导出CSV
表 4 正交表和AVG统计
Table 4 Orthogonal array and AVG
参数组合 水平 $ AVG $ $ popsize $ $ TF $ $ r_{m} $ 1 1 1 1 500.65 2 1 2 2 503.90 3 1 3 3 497.30 4 1 4 4 498.55 5 2 1 2 489.35 6 2 2 3 491.20 7 2 3 4 485.50 8 2 4 1 488.35 9 3 1 3 482.55 10 3 2 4 481.80 11 3 3 1 482.25 12 3 4 2 483.25 13 4 1 4 483.35 14 4 2 1 484.00 15 4 3 2 483.60 16 4 4 3 482.20
下载: 导出CSV
表 5 各参数响应值
Table 5 Average response value and rank of each parameter
水平 $ popsize $ $ TF $ $ r_{m} $ 1 500.10 488.98 488.81 2 488.60 490.23 490.02 3 482.46 487.16 488.31 4 483.29 488.09 487.30 等级 1 3 2
下载: 导出CSV
表 6 DTLBO与PSO、DTLBO-Ⅰ、标准TLBO和CIWO的比较($ \rho =4 $)
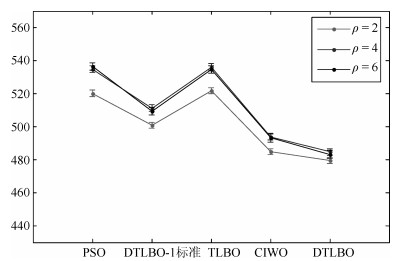
Table 6 Comparisons of DTLBO, DTLBO-Ⅰ, PSO, CIWO, and standard TLBO ($ \rho =4 $)
测试问题 PSO DTLBO-Ⅰ 标准TLBO CIWO DTLBO BST WST AVG BST WST AVG BST WST AVG BST WST AVG BST WST AVG 10$ \times $5 229 235 230.15 228 231 229.45 228 233 230.05 227 246 229.95 227 244 229.3 20$ \times $5 560 587 576.7 546 579 560.3 558 589 574.5 503 554 526.5 506 534 521.4 30$ \times $5 682 708 694.8 638 685 662.3 675 709 697 615 665 635.5 607 638 622.4 40$ \times $5 752 784 771.4 696 748 725.7 728 787 767.75 654 716 690.05 661 716 692.8 50$ \times $5 1 132 1 171 1 157.45 1 093 1 140 1 114.3 1148 1 175 1 161.5 1 019 1 091 1 059.2 1 019 1 078 1 051.85 40$ \times $10 340 357 348.2 307 336 321.3 340 360 351.15 293 326 311.9 284 317 304.3 50$ \times $10 410 429 419.7 373 411 392.75 413 429 421.1 362 391 376.3 353 386 370.75 60$ \times $10 523 548 538.8 497 529 516 538 552 544.3 485 516 499.95 481 516 500.6 70$ \times $10 658 682 672 626 653 641.8 660 684 672.65 604 639 622 597 636 621.75 80$ \times $10 596 619 612.15 567 601 585.55 597 621 612.95 553 589 571.45 553 584 569.5 80$ \times $20 286 298 292.2 265 289 278.85 285 298 291.8 257 282 271.65 259 272 264.7 90$ \times $20 287 299 294.65 271 289 280.55 288 301 297.4 255 284 273.1 255 279 269.05 100$ \times $20 329 340 336 309 328 320.5 333 343 338 304 323 312.65 299 313 306.25 150$ \times $20 479 496 489.2 460 486 472 487 499 492.9 454 476 464.95 449 477 458.45 200$ \times $20 575 593 587.25 557 576 568.5 577 598 589.85 559 575 564.4 547 559 549.55 Average 522.53 543.06 534.71 495.53 525.4 511.32 523.66 545.2 536.19 476.27 511.53 493.97 473.13 503.27 488.84
下载: 导出CSV
表 7 HDTLBO与DPSO、DTLBO-Ⅱ、GA_DR_C和CCIWO的比较($ \rho =4 $)
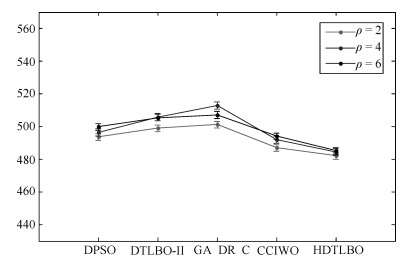
Table 7 Comparisons of HDTLBO, DPSO, DTLBO-Ⅱ, GA_DR_C, and CCIWO ($ \rho =4 $)
测试问题 DPSO DTLBO-Ⅱ GA_DR_C CCIWO HDTLBO BST WST AVG BST WST AVG BST WST AVG BST WST AVG BST WST AVG 10$ \times $5 227 230 228.75 227 230 228.45 227 230 228.2 227 230 228.2 227 230 227.3 20$ \times $5 521 547 527.15 533 554 543.1 514 551 536.15 494 536 518.1 499 540 520.95 30$ \times $5 612 647 624.1 630 658 645.65 625 656 645.85 617 644 621.95 603 638 617.5 40$ \times $5 652 692 686.75 695 733 710.15 695 735 715.8 657 715 686.15 645 692 681.65 50$ \times $5 1 014 1 074 1 058.4 1 064 1 111 1 090 1 070 1107 1 094.75 1 024 1 088 1 057.05 1 006 1 055 1 035.9 40$ \times $10 303 317 306.14 303 328 316.2 305 325 316.4 292 320 307.7 290 316 303.65 50$ \times $10 365 387 370.95 370 395 387.95 374 400 388.2 362 390 373.85 355 382 369 60$ \times $10 481 503 498.85 498 519 510.9 497 584 541.15 481 515 496.6 481 501 493.05 70$ \times $10 601 639 615.4 626 656 640.15 636 716 694.55 597 639 621.7 597 635 606.75 80$ \times $10 556 590 579 571 596 584.55 561 590 582.75 548 586 568.45 554 575 564.85 80$ \times $20 274 285 277.41 269 285 278 273 285 279.9 275 280 269.3 262 279 273.7 90$ \times $20 269 290 273.33 275 288 282.1 277 292 285.8 268 285 276.25 266 282 272.58 100$ \times $20 304 323 313.7 313 327 320.85 317 328 322.85 300 323 314.6 297 323 310.65 150$ \times $20 472 489 475.34 469 486 476.45 470 488 480.55 469 486 470.7 464 483 469.89 200$ \times $20 553 579 566.5 564 579 573 562 587 578.1 557 583 570.05 549 579 565.2 Average 480.27 506.13 493.45 493.8 516.33 505.83 493.53 524.93 521.73 477.87 508 492.04 473 500.67 487.51
下载: 导出CSV
表 8 模具各工序加工约束及首次到达时间表
Table 8 The schedule of mold process constraint and arrival time
模具 可执行操作的设备 模具首次到达设备时间 操作1 操作2 操作3 m1 m2 m3 m4 m5 1 m1/m3/m5 m3/m4 m2/m3/m4 7 4 8 4 6 2 m1/m3/m6 m1 — 1 6 2 3 3 3 m3 — — 3 1 8 4 6 4 m2/m3/m5 m1/m2/m3/m4/m5 m2/m3/m4 8 1 6 8 7 5 m1/m3/m4 — — 1 2 6 7 3 6 m2/m5 m1/m4/m5 m1/m4/m5 5 8 3 1 5 7 m2/m4/m5 m2/m3/m4/m5 — 3 8 3 3 6 8 m1/m2/m3/m5 — — 2 6 8 7 7 9 m4/m5 m3 m3/m4 6 3 5 3 7 10 m2 m2/m4 m1/m2/m3 7 4 1 4 6 11 m1/m5 m1 — 6 5 1 8 4 12 m4/m5 m1/m2/m3/m4/m5 m1/m2/m4 5 3 1 8 8 13 m2/m4/m5 m3 m4/m5 7 1 6 6 6 14 m3 m1/m3/m5 2 1 4 6 3 15 m3/m4/m5 — — 8 6 5 3 2 16 m1/m3 m3 — 8 6 6 7 2 17 m3 — — 8 4 6 7 1 18 m4/m5 m2/m4 m5 4 3 5 2 6 19 m1/m2/m4/m5 — — 3 6 2 1 3 20 m1/m4 m3/m5 m2/m4/m5 4 7 5 7 7
下载: 导出CSV
表 9 各模具产品的序相关设置时间表
Table 9 The schedule of sequence setup time between each mold
模具 序相关设置时间 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 — 2 3 3 4 3 3 3 3 2 1 3 1 4 4 4 2 4 2 1 2 2 — 2 2 3 2 2 1 3 1 2 2 4 4 3 3 4 4 2 4 3 2 3 — 4 3 3 4 2 1 2 3 3 1 4 2 1 3 3 4 3 4 3 1 3 — 4 1 4 2 2 2 1 1 4 1 3 2 2 1 2 3 5 4 4 4 2 — 1 1 1 4 1 1 1 3 2 1 3 2 4 3 3 6 1 2 3 2 3 — 3 2 2 3 4 1 1 3 3 2 4 2 4 1 7 3 4 4 4 1 2 — 1 1 4 2 2 3 2 2 2 4 1 1 2 8 4 2 4 1 4 1 2 — 4 3 3 3 2 4 1 3 4 1 4 1 9 4 2 3 3 2 4 4 1 — 2 2 3 2 1 2 4 2 1 4 3 10 2 4 1 2 2 4 4 3 3 — 1 1 2 3 1 2 1 4 2 1 11 3 4 3 2 2 2 1 2 2 2 — 2 4 3 3 2 1 2 2 2 12 2 1 4 2 4 2 3 2 1 2 3 — 1 1 3 2 3 2 1 2 13 2 1 2 4 2 1 4 2 4 2 4 3 — 4 4 3 4 3 4 1 14 4 4 1 3 2 2 2 4 1 4 1 2 1 — 2 2 1 3 4 1 15 3 2 2 3 1 2 3 4 3 1 2 1 3 1 — 2 3 1 4 4 16 1 4 1 1 4 3 1 3 1 2 4 4 2 3 4 — 4 4 4 1 17 4 3 1 1 3 2 3 1 3 4 1 1 3 2 1 1 — 2 1 1 18 1 2 4 4 2 1 4 1 2 1 4 4 3 2 1 3 1 — 2 2 19 2 3 2 2 2 3 4 1 1 3 2 2 2 3 3 2 4 1 — 2 20 2 2 2 2 2 2 2 1 2 1 2 4 1 4 1 1 1 4 1 —
下载: 导出CSV
表 10 模具各工序的加工时间表
Table 10 The processing time table of each mold
模具 操作1 操作2 操作3 m1 m2 m3 m4 m5 m1 m2 m3 m4 m5 m1 m2 m3 m4 m5 1 27 — 18 — 29 — — 27 17 — — 23 29 19 — 2 13 — 26 — 11 13 — — — — — — — — — 3 — — 23 — — — — — — — — — — — — 4 — 10 13 — 12 18 25 11 10 26 — 21 31 27 — 5 9 — 8 16 — — — — — — — — — — — 6 — 9 — — 29 19 — — 25 10 30 — — 26 19 7 — 19 — 22 28 — 10 28 24 27 — — — — — 8 30 23 28 — 17 — — — — — — — — — — 9 — — — 31 24 — — 9 — — — — 8 28 — 10 — 25 — — — — 27 — 13 — 31 20 26 — — 11 25 — — — 24 12 — — — — — — — — — 12 — — — 23 — 17 13 16 — — 22 8 — 30 — 13 — 16 — 19 22 — — 28 — — — — — 27 23 14 28 — 16 — 20 — — 18 — — 16 — 16 — 21 15 — — 28 29 23 — — — — — — — — — — 16 27 — 10 — — — — 8 — — — — — — — 17 — — 26 — — — — — — — — — — — — 18 — — — 12 24 — 13 — 27 — — — — — 17 19 24 19 — 12 14 — — — — — — — — — — 20 17 — — 10 — — — 31 — 20 — 30 — 9 24
下载: 导出CSV
表 11 实例仿真结果
Table 11 Simulation results of the instance
运行次数 DTLBO-Ⅱ GA DPSO CCIWO HDTLBO 1 167 166 166 163 163 2 164 166 164 163 166 3 168 167 167 167 167 4 169 166 164 166 163 5 163 163 165 163 165 6 167 165 166 167 163 7 167 168 163 168 166 8 166 168 167 164 168 9 168 167 164 163 163 10 169 168 165 164 165 11 168 163 164 168 166 12 169 168 169 167 163 13 168 167 165 166 167 14 163 170 166 170 166 15 167 166 168 169 163 16 166 167 166 171 163 17 167 170 163 168 163 18 169 168 164 170 165 19 165 168 163 165 168 20 167 168 164 167 163 Average 166.85 166.95 165.15 166.45 164.8
下载: 导出CSV
-
[1] Pinedo M. Scheduling: theory, algorithms, and systems. Berlin Heidelberg: Springer, 2012. [2] Allahverdi A. Two-machine proportionate flowshop scheduling with breakdowns maximum lateness. Computers & Operations Research, 1996, 23(10): 909-916 [3] Lan X J, Su D D. Research of a mold job shop scheduling optimization based on particle swarm optimization algorithm. Applied Mechanics & Materials, 2015, 757(2): 201-207 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.4028/www.scientific.net/AMM.757.201 [4] Sang H Y, Duan P Y, Li J Q. An effective invasive weed optimization algorithm for scheduling semiconductor final testing problem. Swarm & Evolutionary Computation, 2018, 38: 42-53 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f24ee1e67ed4add61940b0e69b5f0a53 [5] Hu H, Ng KKH, Qin Y C. Robust parallel machine scheduling problem with uncertainties and sequence-dependent setup time. Scientific Programming, 2016: 1-13 [6] Li C L, Cheng T C E. The parallel machine min-max weighted absolute lateness scheduling problem. Naval Research Logistics, 1994, 41(1): 33-46 doi: 10.1002/1520-6750(199402)41:1<33::AID-NAV3220410104>3.0.CO;2-S [7] Ranjbar M, Davari M, Leus R. Two branch-and-bound algorithms for the robust parallel machine scheduling problem. Computers & Operations Research, 2012, 39(7): 1652-1660 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=58dbb13e91377bee19b577c7d4561726 [8] Lee W C, Wang J Y, Lin M C. A branch-and-bound algorithm for minimizing the total weighted completion time on parallel identical machines with two competing agents. Knowledge-Based Systems, 2016, 105(C): 68-82 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=90998daca3d98ce1fbd2b119fbae1b4a [9] Wu L, Wang S. Exact and heuristic methods to solve the parallel machine scheduling problem with multi-processor tasks. International Journal of Production Economics, 2018, 201: 26-40 doi: 10.1016/j.ijpe.2018.04.013 [10] Chen Z L, Powell W B. A column generation based decomposition algorithm for a parallel machine just-in-time scheduling problem. European Journal of Operational Research, 1999, 116(1): 220-232 doi: 10.1016/S0377-2217(98)00136-2 [11] Yin Y, Ye D, Zhang G. Single machine batch scheduling to minimize the sum of total flow time and batch delivery cost with an unavailability interval. Information Sciences, 2014, 274(8): 310-322 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=057211486faaa3fa789b3f4b9a751866 [12] Li D W, Lu X W. Two-agent parallel-machine scheduling with rejection. Theoretical Computer Science, 2017, 703: 66-75 doi: 10.1016/j.tcs.2017.09.004 [13] Yin Y, Cheng S R, Cheng T C E, et al. Just-in-time scheduling with two competing agents on unrelated parallel machines. Omega, 2016, 63: 41-47 doi: 10.1016/j.omega.2015.09.010 [14] Woo Y B, Jung S, Kim B S. A rule-based genetic algorithm with an improvement heuristic for unrelated parallel machine scheduling problem with time-dependent deterioration and multiple rate-modifying activities. Computers & Industrial Engineering, 2017, 109: 179-190 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f0a6c39ef977f0f9c653802880bf2420 [15] Avalos-Rosales O, Angel-Bello F, Alvarez A. Efficient metaheuristic algorithm and re-formulations for the unrelated parallel machine scheduling problem with sequence and machine-dependent setup times. International Journal of Advanced Manufacturing Technology, 2015, 76(9-12): 1705-1718 doi: 10.1007/s00170-014-6390-6 [16] 张嘉琦, 曹政才, 刘民.融合代理模型和差分进化算法的并行机动态调度方法.计算机集成制造系统, 2017, 23(1): 75-81 http://d.old.wanfangdata.com.cn/Periodical/jsjjczzxt201701009Zhang Jia-Qi, Cao Zheng-Cai, Liu Min. Integrated differential evolution algorithm with surrogate model for dynamic parallel machine scheduling. Computer Integrated Manufacturing Systems, 2017, 23(1): 75-81 http://d.old.wanfangdata.com.cn/Periodical/jsjjczzxt201701009 [17] Chen C L. Iterated hybrid metaheuristic algorithms for unrelated parallel machines problem with unequal ready times and sequence-dependent setup times. International Journal of Advanced Manufacturing Technology, 2012, 60(5-8): 693-705 doi: 10.1007/s00170-011-3623-9 [18] Damodaran P, Diyadawagamage D A, Ghrayeb O. A particle swarm optimization algorithm for minimizing makespan of nonidentical parallel batch processing machines. International Journal of Advanced Manufacturing Technology, 2012, 58(9-12): 1131-1140 doi: 10.1007/s00170-011-3442-z [19] Diana R O M. An immune-inspired algorithm for an unrelated parallel machines$'$ scheduling problem with sequence and machine dependent setup-times for makespan minimisation. Neurocomputing, 2015, 163(C): 94-105 [20] Sels V, Coelho J, Dias A M, et al. Hybrid tabu search and a truncated branch-and-bound for the unrelated parallel machine scheduling problem. Computers & Operations Research, 2015, 53: 107-117 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a7d0c31a9a95e9f1ce534a14dda1cdb2 [21] Bitar A, Yugma C, Roussel R. A memetic algorithm to solve an unrelated parallel machine scheduling problem with auxiliary resources in semiconductor manufacturing. Journal of Scheduling, 2016, 19(4): 367-376 doi: 10.1007/s10951-014-0397-6 [22] Joo C M, Kim B S. Hybrid genetic algorithms with dispatching rules for unrelated parallel machine scheduling with setup time and production availability. Computers & Industrial Engineering, 2015, 85(C): 102-109 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fcb17bbd465d8682d2400ec1e2f8025a [23] 罗家祥, 唐立新.带释放时间的并行机调度.问题的ILS & SS算法.自动化学报, 2005, 31(6): 917-924 http://www.aas.net.cn/article/id/15921Luo Jia-Xiang, Tang Li-Xin. A new ILS & SS algorithm for parallel-machine scheduling problem. Acta Automatica Sinica, 2005, 31(6): 917-924 http://www.aas.net.cn/article/id/15921 [24] Lin S W, Ying K C. ABC-based manufacturing scheduling for unrelated parallel machines with machine-dependent and job sequence-dependent setup times. Computers & Operations Research, 2014, 51(3): 172-181 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=5b16d15a9448bceeb8e453a1f542ce32 [25] Rao R V, Savsani V J. and Vakharia D P. Teaching- learning-based optimization: a novel method for constrained mechanical design optimization problems. Computer-Aided Design, 2011, 43(3): 303-315 doi: 10.1016/j.cad.2010.12.015 [26] Waghmare, G. Comments on "a note on teaching-learning-based optimization algorithm". Information Sciences, 2013, 229: 159-169 doi: 10.1016/j.ins.2012.11.009 [27] Shao S W, Pi D C, Shao Z. An extended teaching-learning based optimization algorithm for solving no-wait flow shop scheduling problem. Applied Soft Computing, 2017, 61: 193-210 doi: 10.1016/j.asoc.2017.08.020 [28] Xu Y, Wang L, Wang S Y, et al. An effective teaching--learning-based optimization algorithm for the flexible job-shop scheduling problem with fuzzy processing time. Neurocomputing, 2015, 148: 260-268 doi: 10.1016/j.neucom.2013.10.042 [29] Shao S W, Pi D C, Shao Z. A hybrid discrete optimization algorithm based on teaching-probabilistic learning mechanism for no-wait flow shop scheduling. Knowledge-Based Systems, 2016, 107: 219-234 doi: 10.1016/j.knosys.2016.06.011 [30] Li J Q, Pan Q K, Mao K. A discrete teaching-learning-based optimisation algorithm for realistic flowshop rescheduling problems. Engineering Applications of Artificial Intelligence, 2015, 37: 279-292 doi: 10.1016/j.engappai.2014.09.015 [31] 马永杰, 云文霞.遗传算法研究进展.计算机应用研究, 2012, 29(4): 1201-1206 doi: 10.3969/j.issn.1001-3695.2012.04.001Ma Yong-Jie, Yun Wen-Xia. Research progress of genetic algorithm. Application Rehash of Computers, 2012, 29(4): 1201-1206 doi: 10.3969/j.issn.1001-3695.2012.04.001 [32] Abdoun O, Abouchabaka J. A comparative study of adaptive crossover operators for genetic algorithms to resolve the traveling salesman problem. Computer Science, 2011, 31(11): 49-57 [33] 王凌, 钱斌.混合差分进化与调度算法.北京:清华大学出版社, 2012.Wang Ling, Qian Bin. Hybrid differential evolution and scheduling algorithms. Beijing: Tsinghua University Press, 2012. [34] 潘全科, 王凌, 赵保华.解决零空闲流水线调度问题的离散粒子群算法.控制与决策, 2008, 23(2): 191-194 doi: 10.3321/j.issn:1001-0920.2008.02.014Pan Quan-Ke, Wang Ling, Zhao Bao-Hua. Discrete particle swarm optimization for no-idle flow shop problem. Control and Decision, 2008, 23(2): 191-194 doi: 10.3321/j.issn:1001-0920.2008.02.014 -
点击查看大图
图(7) / 表(11)
计量
- 文章访问数: 6138
- HTML全文浏览量: 1546
- PDF下载量: 178
- 被引次数: 0
