Data-driven Dual-rate Control for Mixed Separation Thickening Process in a Wireless Network Environment
-
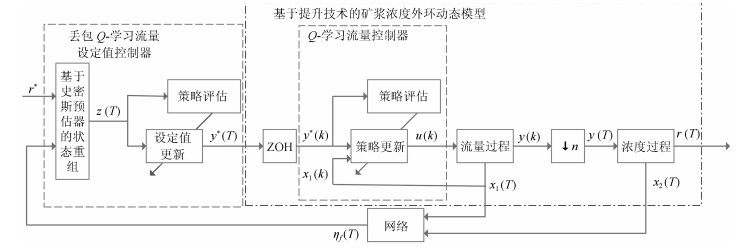
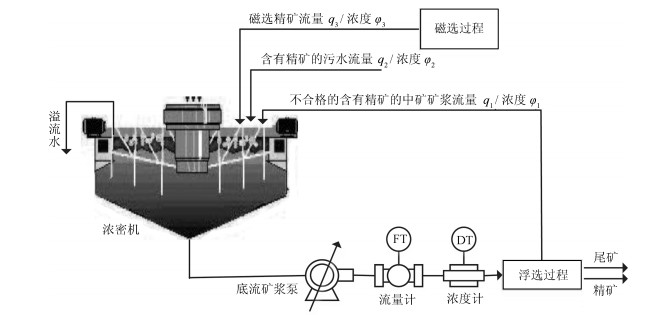
摘要: 无线网络环境下赤铁矿混合选别浓密过程控制问题是以底流矿浆泵频率为内环输入，以底流矿浆流量为内环输出外环输入，以底流矿浆浓度为外环输出的非线性串级工业过程控制问题.其外环反馈回路存在丢包，且模型参数难以辨识，故本文利用工业运行过程的在线数据，设计不依赖模型参数的跟踪控制器.首先，利用浓密过程运行在工作点附近的特点进行线性化，对流量过程设计Q-学习控制器，保证流量过程能够跟踪给定的流量设定值；然后采用提升技术，得到统一时间尺度的以底流矿浆流量设定值为输入，以底流矿浆浓度为输出的被控对象；最后，考虑到在无线网络环境下浓度过程存在反馈丢包，当前的状态可能无法获得，故采用史密斯预估器的思想，利用历史的数据估计系统当前的状态，设计丢包Q-学习设定值控制器为流量过程提供最优设定值.通过仿真实验验证所提算法的有效性.Abstract: The mixed separation thickening process (MSTP) of hematite beneficiation in a wireless network environment is a nonlinear cascade process with the frequency of underflow slurry pump as the inner loop input, the slurry flow-rate as the inner loop output and the concentration as the outer loop output. The dropout occurs in the outer feedback loop, making it difficult to identify the parameters of the model, so the tracking controller only using the data generated by operational processes and independent of the knowledge of model parameters is designed in this paper. First, linearize the thickening system near the steady states, then design a controller based on Q-learning algorithm to make the inner process trace the set-point of the slurry flow-rate. Second, use the lifting technology to obtain the uniform time scale controlled object with the set-point of the slurry flow-rate as the input and the concentration as the output. Finally, considering that the networked-induced feedback dropout exists in the feedback process, meaning the current state information may be lost, a novel Smith predictor is developed to predict the current state from historical measured data, and a dropout Q-learning method is designed to provide the optimal set-point of lower loop. A simulation experiment on MSTP is given to show the effectiveness of the proposed method.
-
Key words:
- Mixed separation thickening process /
- Q-learning /
- dropout /
- Smith predictor
1) 本文责任编委 侯忠生 -
图 2 数据驱动的无线网络下浓密过程的控制结构图
Fig. 2 Structure diagram of data-driven for MSTP under wireless network environment
图 3 浓密过程中浓度、流量的跟踪曲线以及底流泵转速的输入的曲线
Fig. 3 The tracing result of the slurry concentration and the slurry flow-rate, and the input of the frequency of slurry pump
图 5 流量过程Q-学习的结果
Fig. 5 The result of the slurry flow-rate process during the Q-learning process
图 6 浓度过程控制增益$\tilde L$的收敛过程
Fig. 6 Convergence of $\tilde L$to its optimal value $\tilde L$*
图 7 浓度过程丢包Q-学习的结果
Fig. 7 The result of the slurry concentration process during the dropout Q-learning process
图 8 浓度过程Q-学习的结果
Fig. 8 The result of the slurry concentration process during the Q-learning process
表 1 浓密过程符号表
Table 1 Mixed separation thickening process symbol table
符号 物理含义 符号 物理含义 $S$ 浓密机横截面积 $\frac{{\Delta \rho (t)}}{{g\rho (\cdot)}}$ 泵两端管路单位重量
矿浆的势能差$\mu$ 介质的粘度 $D$ 阻力损失 $p$ 平均浓度系数 $k_i$, $\bar{K}$ 与浓密机结构有关的常数 $p _s$ 矿浆内固体密度 $g$ 重力加速度 $p _l$ 矿浆内液体密度 $\theta(t)$ 干扰 $k_{0}$ 静态放大系数 $h(\cdot)$ 泥层界面高度 $\tau$ 时间常数 ${v_p}(\cdot)$ 矿浆颗粒沉降速度 ${\varphi _1}$ 浮选中矿矿浆浓度 ${q_1}$ 浮选中矿流量 ${\varphi _2}$ 污水浓度 ${q_2}$ 污水流量 ${\varphi _3}$ 磁选精矿矿浆浓度 ${q_3}$ 磁选精矿矿浆流量 
下载: 导出CSV
表 2 对比实验2和3评价指标
Table 2 Performance index of comparison experiment
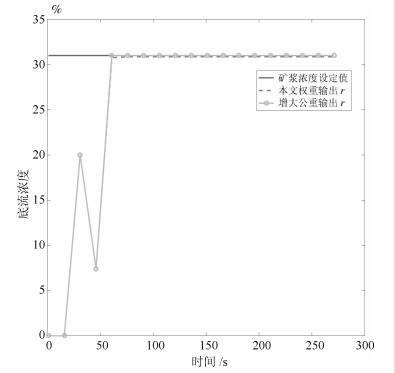
IAE MSE 本文$Q_2$ 8.4224 0.0191 未丢包 8.4093 0.0190 增大$Q_2$ 0.0418 6.63$\times 10^{-7}$
下载: 导出CSV
-
[1] Diehl S. A regulator for continuous sedimentation in ideal clarifier-thickener units. Journal of Engineering Mathematics, 2008, 60(3-4):265-291 doi: 10.1007/s10665-007-9149-3 [2] Betancourt F, Bürger R, Diehl S, Farås S. Modeling and controlling clarifier-thickeners fed by suspensions with time-dependent properties. Minerals Engineering, 2014, 62:91-101 doi: 10.1016/j.mineng.2013.12.011 [3] Cao X H, Cheng P, Chen J M, Sun Y X. An online optimization approach for control and communication codesign in networked cyber-physical systems. IEEE Transactions on Industrial Informatics, 2013, 9(1):439-450 doi: 10.1109/TII.2012.2216537 [4] Fan J L, Jiang Y, Chai T Y. MPC-based setpoint compensation with unreliable wireless communications and constrained operational conditions. Neurocomputing, 2017, 270:110-121 doi: 10.1016/j.neucom.2016.10.098 [5] 范家璐, 姜艺, 柴天佑.无线网络环境下工业过程运行反馈控制方法.自动化学报, 2016, 42(8):1166-1174 http://www.aas.net.cn/CN/abstract/abstract18906.shtmlFan Jia-Lu, Jiang Yi, Chai Tian-You. Operational feedback control of industrial processes in a wireless network environment. Acta Automatica Sinica, 2016, 42(8):1166-1174onumber http://www.aas.net.cn/CN/abstract/abstract18906.shtml [6] Sidrak Y L. Control of the thickener operation in alumina production. Control Engineering Practice, 1997, 5(10):1417-1426 doi: 10.1016/S0967-0661(97)00138-X [7] 李海波, 柴天佑, 赵大勇.混合选别浓密机底流矿浆浓度和流量区间智能切换控制方法.自动化学报, 2014, 40(9):1967-1975 http://www.aas.net.cn/CN/abstract/abstract18467.shtmlLi Hai-Bo, Chai Tian-You, Zhao Da-Yong. Intelligent switching control of underflow slurry concentration and flowrate intervals in mixed separation thickener. Acta Automatica Sinica, 2014, 40(9):1967-1975onumber http://www.aas.net.cn/CN/abstract/abstract18467.shtml [8] Chai T Y, Jia Y, Li H B, Wang H. An intelligent switching control for a mixed separation thickener process. Control Engineering Practice, 2016, 57:61-71 doi: 10.1016/j.conengprac.2016.07.007 [9] 王琳岩, 李健, 贾瑶, 柴天佑.混合选别浓密过程双速率智能切换控制.自动化学报, 2018, 44(2):330-343 http://www.aas.net.cn/CN/abstract/abstract19228.shtmlWang Lin-Yan, Li Jian, Jia Yao, Chai Tian-You. Dual-rate intelligent switching control for mixed separation thickening process. Acta Automatica Sinica, 2018, 44(2):330-343onumber http://www.aas.net.cn/CN/abstract/abstract19228.shtml [10] Jiang Y, Fan J L, Chai T Y, Chen T W. Setpoint dynamic compensation via output feedback control with network induced time delays. In:Proceedings of the 2015 American Control Conference (ACC). Chicago, IL, USA:IEEE, 2015. 5384-5389 [11] Schenato L, Sinopoli B, Franceschetti M, Poolla K, Sastry S S. Foundations of control and estimation over lossy networks. Proceedings of the IEEE, 2007, 95(1):163-187 doi: 10.1109/JPROC.2006.887306 [12] Sinopoli B, Schenato L, Franceschetti M, Poolla K, Jordan M I, Sastry S S. Kalman filtering with intermittent observations. IEEE Transactions on Automatic Control, 2004, 49(9):1453-1464 doi: 10.1109/TAC.2004.834121 [13] Shi Y, Yu B. Robust mixed H2/H∞ control of networked control systems with random time delays in both forward and backward communication links. Automatica, 2011, 47(4):754-760 doi: 10.1016/j.automatica.2011.01.022 [14] Zhang H, Shi Y, Wang J M. Observer-based tracking controller design for networked predictive control systems with uncertain Markov delays. International Journal of Control, 2013, 86(10):1824-1836 doi: 10.1080/00207179.2013.797107 [15] Zhang J H, Lin Y J, Shi P. Output tracking control of networked control systems via delay compensation controllers. Automatica, 2015, 57:85-92 doi: 10.1016/j.automatica.2015.04.006 [16] Jiang Y, Fan J L, Chai T Y, Li J N, Lewis F L. Data-driven flotation industrial process operational optimal control based on reinforcement learning. IEEE Transactions on Industrial Informatics, 2018, 14(5):1974-1989 doi: 10.1109/TII.2017.2761852 [17] Gao W N, Jiang Z P, Lewis F L, Wang Y B. Leader-to-formation stability of multi-agent systems:an adaptive optimal control approach. IEEE Transactions on Automatic Control, 2018, 63(10):3581-3587 doi: 10.1109/TAC.2018.2799526 [18] Gao W N, Jiang Z P. Learning-based adaptive optimal tracking control of strict-feedback nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(6):2614-2624 doi: 10.1109/TNNLS.2017.2761718 [19] Xu H, Sahoo A, Jagannathan S. Stochastic adaptive event-triggered control and network scheduling protocol co-design for distributed networked systems. IET Control Theory & Applications, 2014, 8(18):2253-2265 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f947c6504d4b00d6e31cd0253ba2ad40 [20] Xu H, Jagannathan S, Lewis F L. Stochastic optimal control of unknown linear networked control system in the presence of random delays and packet losses. Automatica, 2012, 48(6):1017-1030 doi: 10.1016/j.automatica.2012.03.007 [21] Xu H, Jagannathan S. Stochastic optimal controller design for uncertain nonlinear networked control system via neuro dynamic programming. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(3):471-484 doi: 10.1109/TNNLS.2012.2234133 [22] Kim B H, Klima M S. Development and application of a dynamic model for hindered-settling column separations. Minerals Engineering, 2004, 17(3):403-410 doi: 10.1016/j.mineng.2003.11.013 [23] Zheng Y Y. Mathematical Mode of Anaerobic Processes Applied to the Anaerobic Sequencing Batch Reactor[Ph.D. dissertation], University of Toronto, Canada, 2003 [24] Jiang Y, Fan J L, Chai T Y, Lewis F L, Li J N. Tracking control for linear discrete-time networked control systems with unknown dynamics and dropout. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10):4607-4620 doi: 10.1109/TNNLS.2017.2771459 [25] 姜艺. 浮选过程运行反馈双率区间切换控制方法[硕士学位论文], 东北大学, 中国, 2016Jiang Yi. Operational Feedback Multi-rate Interval Switch Control of Flotation Processes[Master thesis], Northeastern University, China, 2016onumber [26] Kiumarsi B, Lewis F L, Modares H, Karimpour A, Naghibi-Sistani M B. Reinforcement Q-learning for optimal tracking control of linear discrete-time systems with unknown dynamics. Automatica, 2014, 50(4):1167-1175 doi: 10.1016/j.automatica.2014.02.015 [27] Al-Tamimi A, Lewis F L, Abu-Khalaf M. Model-free Q-learning designs for linear discrete-time zero-sum games with application to H-infinity control. Automatica, 2007, 43(3):473-481 doi: 10.1016/j.automatica.2006.09.019 [28] Gao W N, Huang M Z, Jiang Z P, Chai T Y. Sampled-data-based adaptive optimal output-feedback control of a 2-degree-of-freedom helicopter. IET Control Theory & Applications, 2016, 10(12):1440-1447 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=492a5768c546986177b1236275ae85ca [29] 姜艺, 范家璐, 贾瑶, 柴天佑.数据驱动的浮选过程运行反馈解耦控制方法.自动化学报, 2019, 45(4):759-770 http://www.aas.net.cn/CN/abstract/abstract19477.shtmlJiang Yi, Fan Jia-Lu, Jia Yao, Chai Tian-You. Data-driven flotation process operational feedback decoupling control. Acta Automatica Sinica, 2019, 45(4):759-770 http://www.aas.net.cn/CN/abstract/abstract19477.shtml -
图(10) / 表(2)
计量
- 文章访问数: 2380
- HTML全文浏览量: 261
- PDF下载量: 376
- 被引次数: 0
