基于<i>θ</i>-D方法的欠驱动TORA系统非线性最优控制

张宇; 李芦钰; 郭源博; 张晓华

doi:10.16383/j.aas.c180032

基于θ-D方法的欠驱动TORA系统非线性最优控制

doi: 10.16383/j.aas.c180032

张宇^1,,
李芦钰^2, ,,
郭源博^1,,
张晓华^1,

1.
大连理工大学电气工程学院大连 116024
2.
大连理工大学土木工程学院大连 116024

基金项目:

国家自然科学基金项目 51377013

国家自然科学基金项目 51378093

详细信息

作者简介:
张宇大连理工大学电气工程学院博士研究生. 2016年获得大连理工大学电气工程学院硕士学位.主要研究方向为欠驱动系统控制, 结构振动控制.E-mail: hblwzy@163.com

郭源博大连理工大学讲师. 2012年获得哈尔滨工业大学博士学位.主要研究方向为电力牵引系统容错控制, 无功补偿, 谐波抑制. E-mail: gyb@dlut.edu.cn

张晓华大连理工大学教授. 1998年获得哈尔滨工业大学博士学位.主要研究方向为智能机器人与运动控制, 欠驱动系统控制, 电力电子系统非线性控制. E-mail: xh_zhang@dlut.edu.cn

通讯作者:
李芦钰大连理工大学副教授. 2008年获得哈尔滨工业大学博士学位.主要研究方向为结构振动控制, 智能材料与结构, 结构非线性振动.本文通信作者. E-mail: liluyu@dlut.edu.cn

计量
- 文章访问数: 1244
- HTML全文浏览量: 74
- PDF下载量: 139
- 被引次数: 0
出版历程
- 收稿日期: 2018-01-15
- 录用日期: 2018-03-16
- 刊出日期: 2020-07-24

On the Nonlinear Optimal Control of TORA System Based on θ-D Approximation

ZHANG Yu^1
,,
LI Lu-Yu^{2
, ,},
GUO Yuan-Bo^1
,,
ZHANG Xiao-Hua^1
,

1.
School of Electrical Engineering, Dalian University of Technology, Dalian 116024
2.
School of Civil Engineering, Dalian University of Technology, Dalian 116024

Funds:

National Natural Science Foundation of China 51377013

National Natural Science Foundation of China 51378093

More Information

Author Bio:
ZHANG Yu Ph. D. candidate at the School of Electrical Engineering, Dalian University of Technology. He received his master degree from Dalian University of Technology in 2016. His research interest covers control of underactuated system, and structural vibration control

GUO Yuan-Bo Lecturer at the School of Electrical Engineering, Dalian University of Technology. He received his Ph. D. degree from Harbin Institute of Technology in 2012. His research interest covers fault tolerant control of electric traction system, reactive power compensation, and harmonic suppression

ZHANG Xiao-Hua Professor at the School of Electrical Engineering, Dalian University of Technology. He received his Ph. D. degree from Harbin Institute of Technology in 1998. His research interest covers intelligent robot and motion control, nonlinear control of underactuated system, and nonlinear control of power electronics system

Corresponding author: LI Lu-Yu Associate professor at the School of Civil Engineering, Dalian University of Technology. He received his Ph. D. degree from Harbin Institute of Technology in 2008. His research interest covers structural vibration control, smart material and structure, and nonlinear structural vibration. Corresponding author of this paper

摘要

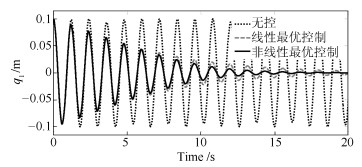
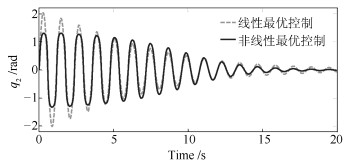
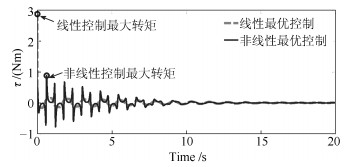
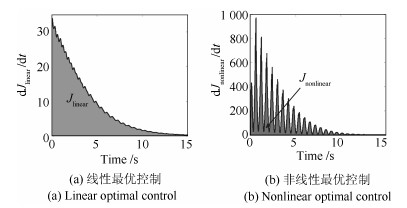
摘要: 针对TORA (Translational oscillator with rotating actuator)系统的镇定控制问题, 提出一种基于$\theta $-D方法的非线性最优控制方案.应用拉格朗日方程建立TORA系统的数学模型, 为保证状态空间形式的TORA系统数学模型中状态向量系数矩阵$A(\pmb{x})$能够分离出常值矩阵, 且其能与控制位置矩阵构成可控对, 采用不同于传统形式的解耦坐标变换对TORA系统进行了处理, 以此为基础为TORA系统设计基于$\theta $-D方法的非线性最优控制器, 该控制方案可离线得到控制输入的显示表达式.通过数值仿真以及与基于局部线性化的线性最优控制方案进行比较, 验证了所提非线性最优控制方案所具有的良好瞬态性能.
- 具有旋转激励的平移振荡器 /
- 最优控制 /
- 坐标变换 /
- 非线性控制 /
- HJB方程
Abstract: A nonlinear optimal control scheme is proposed for the stabilization of TORA (Translational oscillator with rotating actuator) system based on $\theta $-D Approximation in this article. The mathematical model of the nonlinear TORA system is derived through using the Lagrange equations. A novel coordinate transformation is adopted to make it available to isolate a constant matrix from the coefficient matrix $ A({\pmb x})$, and make the constant matrix and the input location vector a controllable pair. The proposed nonlinear optimal control method does not require excessive online computations, as the explicit expression of control input can be derived in controller design phase. Numerical analysis demonstrate the effectiveness of the proposed method and its advantage in instant performance over the linear optimal control approach based on local linearization.
- Translational oscillator with rotating actuator (TORA) /
- optimal control /
- coordinate transformation /
- nonlinear control /
- Hamilton-Jacobi- Bellman (HJB) equation
Recommended by Associate Editor MEI Sheng-Wei
注释:

1) 本文责任编委梅生伟

HTML全文

图 1 TORA系统

Fig. 1 TORA system

下载: 全尺寸图片幻灯片

图 2 控制前后小车位移对比, 小车初始位移$q_{1}(0) = 0.1$ m, 小车初始转角$q_{2}(0) = 0$ rad

Fig. 2 Displacement responses of TORA system with initial condition [$q_{1}(0), q_{2}(0)] = [0.1$ m, 0 rad]

下载: 全尺寸图片幻灯片

图 3 施控时小球转角

Fig. 3 Angle of rotating mass under control

下载: 全尺寸图片幻灯片

图 4 控制转矩

Fig. 4 Control torque

下载: 全尺寸图片幻灯片

图 5 二次型性能指标时间导数

Fig. 5 Time derivative of quadratic cost function

下载: 全尺寸图片幻灯片

图 6 控制转矩做功

Fig. 6 Work done by control torque

下载: 全尺寸图片幻灯片

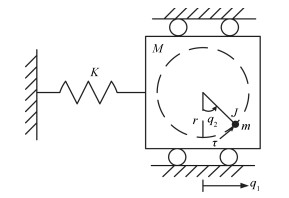
表 1 TORA系统参数

Table 1 Parameters of TORA system

M	10.235	kg
m	0.71	kg
r	0.05	m
J	0.001	kgm²
K	294.87	N/m

下载: 导出CSV

参考文献(30)

[1]	Olfati-Saber R. Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles[Ph. D. dissertation], Massachusetts Institute of Technology, 2001
[2]	盛洋, 赖旭芝, 吴敏.基于模型降阶的平面三连杆欠驱动机械系统位置控制.自动化学报, 2014, 40(7): 1303-1310 doi: 10.3724/SP.J.1004.2014.01303 Sheng Yang, Lai Xu-Zhi, Wu Min. Position control of a planar three-link underactuated mechanical system based on model reduction. Acta Automatica Sinica, 2014, 40(7): 1303-1310 doi: 10.3724/SP.J.1004.2014.01303
[3]	Sun N, Wu Y M, Fang Y C, Chen H. Nonlinear stabilization control of multiple-RTAC systems subject to amplitude-restricted actuating torques using only angular position feedback. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3084-3094 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b1955a21c80295f856f9057d9a3a7ec4
[4]	Pucci D, Romano F, Nori F. Collocated adaptive control of underactuated mechanical systems. IEEE Transactions on Robotics, 2015, 31(6): 1527-1536 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Arxiv000001012436
[5]	Bupp R T, Bernstein D S, Coppola V T. A benchmark problem for nonlinear control design. International Journal of Robust and Nonlinear Control, 1998, 8(4): 307-310 http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1304.1648
[6]	Tsiotras P, Corless M, Rotea M A. An $L_2$ disturbance attenuation solution to the nonlinear benchmark problem. International Journal of Robust and Nonlinear Control, 1998, 8(4): 311-330
[7]	Spong M W. Partial feedback linearization of underactuated mechanical systems. In: Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems. Munich, Germany: IEEE, 1994. 314-321
[8]	Xu L, Hu Q L. Output-feedback stabilisation control for a class of under-actuated mechanical systems. IET Control Theory & Applications, 2013, 7(7): 985-996 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4e5c5c26c84a606968f0e92df035cdf7
[9]	高丙团. TORA的动力学建模及基于能量的控制设计.自动化学报, 2008, 34(9): 1221-1224 doi: 10.3724/SP.J.1004.2008.01221 Gao Bing-Tuan. Dynamical modeling and energy-based control design for TORA. Acta Automatica Sinica, 2008, 34(9): 1221-1224 doi: 10.3724/SP.J.1004.2008.01221
[10]	Gao B T, Bao Y Q, Xie J H, Jia L J. Passivity-based control of two-dimensional translational oscillator with rotational actuator. Transactions of the Institute of Measurement and Control, 2014, 36(1): 111-118 doi: 10.1177/0142331213495438
[11]	武宪青, 何熊熊.欠驱动RTAC系统的自适应耦合控制器设计.自动化学报, 2015, 41(5): 1047-1052 doi: 10.16383/j.aas.2015.c140618 Wu Xian-Qing, He Xiong-Xiong. Adaptive coupling controller design for underactuated RTAC systems. Acta Automatica Sinica, 2015, 41(5): 1047-1052 doi: 10.16383/j.aas.2015.c140618
[12]	Jiang Z P, Kanellakopoulos I. Global output-feedback tracking for a benchmark nonlinear system. IEEE Transactions on Automatic Control, 2000, 45(5): 1023-1027 doi: 10.1109/9.855577
[13]	Karagiannis D, Jiang Z P, Ortega R, Astolfi A. Output-feedback stabilization of a class of uncertain non-minimum-phase nonlinear systems. Automatica, 2005, 41(9): 1609-1615 doi: 10.1016/j.automatica.2005.04.013
[14]	Xu R, Özgüner Ü. Sliding mode control of a class of underactuated systems. Automatica, 2008, 44(1): 233-241 doi: 10.1016/j.automatica.2007.05.014
[15]	Sun N, Wu Y M, Fang Y C, Chen H, Lu B. Nonlinear continuous global stabilization control for underactuated RTAC systems: design, analysis, and experimentation. IEEE/ASME Transactions on Mechatronics, 2017, 22(2): 1104-1115 doi: 10.1109/TMECH.2016.2631550
[16]	Mobayen S. A novel global sliding mode control based on exponential reaching law for a class of underactuated systems with external disturbances. Journal of Computational and Nonlinear Dynamics, 2015, 11(2): 021011 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=62f30278697ca95c645830e9e12a3dd5
[17]	Wu Y M, Sun N, Fang Y C, Liang D K. An increased nonlinear coupling motion controller for underactuated multi-TORA systems: theoretical design and hardware experimentation. IEEE Transactions on Systems, Man, & Cybernetics: Systems, DOI: 10.1109/TSMC.2017.2723478
[18]	Tar J K, Várkonyi T A, Kovács L, Rudas I J, Haidegger T. Robust fixed point transformation based design for model reference adaptive control of a modified TORA system. In: Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago, IL, USA: IEEE, 2014. 123-128
[19]	Gao B T, Ye F. Fuzzy Lyapunov synthesis control of an underactuated 2DTORA system. Journal of Intelligent and Fuzzy Systems, 2015, 28(2): 581-589
[20]	Quan Q, Cai K Y. Repetitive control for TORA benchmark: an additive-state-decomposition-based approach. International Journal of Automation and Computing, 2015, 12(3): 289-296 doi: 10.1007/s11633-015-0885-y
[21]	Zhang Y, Li L Y, Cheng B W, Zhang X H. An active mass damper using rotating actuator for structural vibration control. Advance in Mechanical Engineering, 2016, 8(7): 1-9 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000004718902
[22]	Reddy M P P, Jacob J. Vibration control of flexible link manipulator using SDRE controller and Kalman filtering. Studies in Informatics & Control, 2017, 26(2): 143-150 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bbef186369c1272a2df42a5d5ad8ff82
[23]	Lin L G, Vandewalle J, Liang Y W. Analytical representation of the state-dependent coefficients in the SDRE/SDDRE scheme for multivariable systems. Automatica, 2015, 59: 106-111 doi: 10.1016/j.automatica.2015.06.015
[24]	Xin M, Balakrishnan S N. A new method for suboptimal control of a class of non-linear systems. Optimal Control Applications and Methods, 2005, 26(2): 55-83 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=36990ee88d84019c0e6d8d07da4026cc
[25]	Do T D, Choi H H, Jung J W. $\theta$-D approximation technique for nonlinear optimal speed control design of surface-mounted PMSM drives. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1822-1831 doi: 10.1109/TMECH.2014.2356138
[26]	Gong Q, Ross I M, Fahroo F. Costate computation by a Chebyshev pseudospectral method. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 623-628 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a4a14d14209c3d32d1d49e66aaab701b
[27]	Peng H J, Wang X W, Li M W, Chen B S. An $h_{p}$ symplectic pseudospectral method for nonlinear optimal control. Communications in Nonlinear Science and Numerical Simulation, 2017, 42: 623-644
[28]	戴明祥, 杨新民, 何颖, 易文俊. 3种伪谱最优控制方法的积分形式及统一性证明.控制与决策, 2016, 31(6): 1123-1127 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201606026 Dai Ming-Xiang, Yang Xin-Min, He Ying, Yi Wen-Jun. Integral form and equivalence proof of three pseudospectral optimal control methods. Control and Decision, 2016, 31(6): 1123-1127 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201606026
[29]	Mori T, Deresei I A. A brief summary of the bounds on the solution of the algebraic matrix equations in control theory. International Journal of Control, 1984, 39(2): 247-256 doi: 10.1080/00207178408933163
[30]	Horn R A, Johnson C R. Matrix Analysis. Cambridge: Cambridge University Press, 1985.