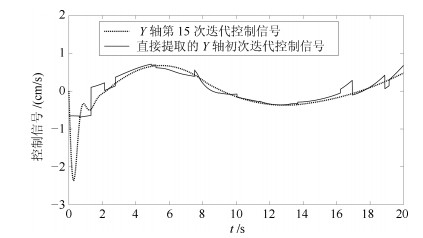
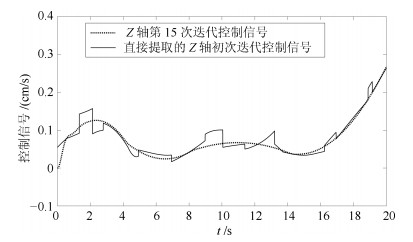
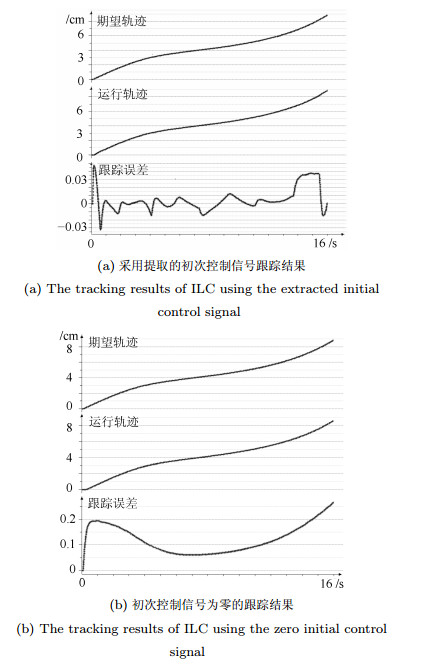
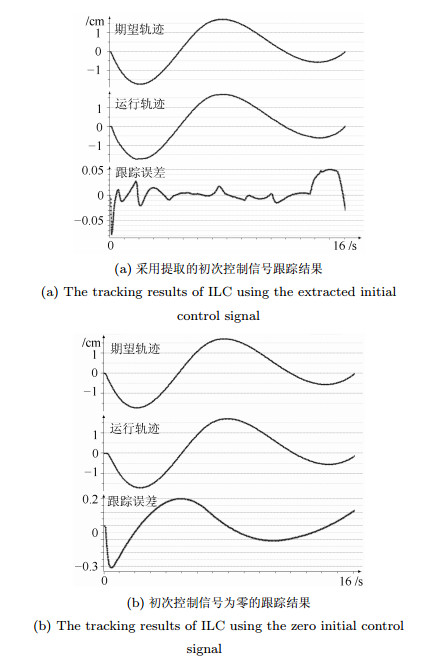
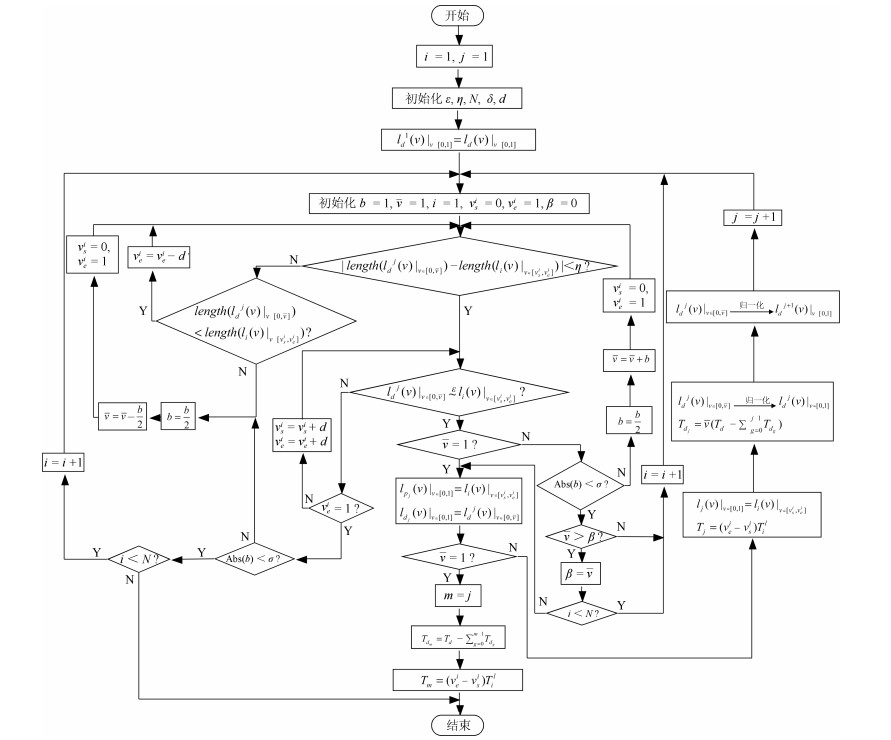
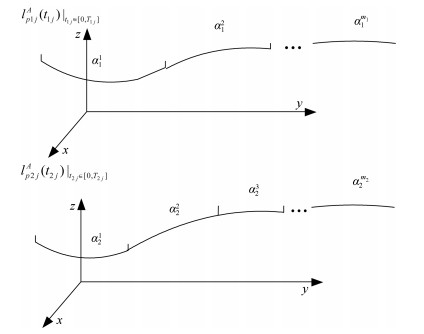
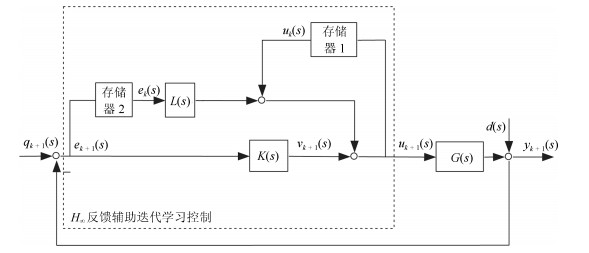
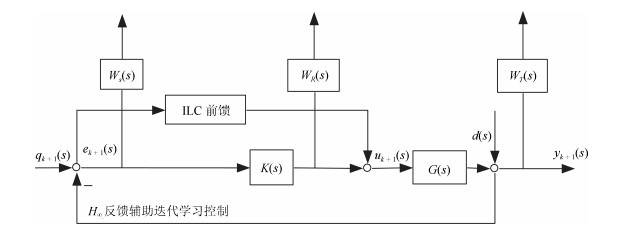
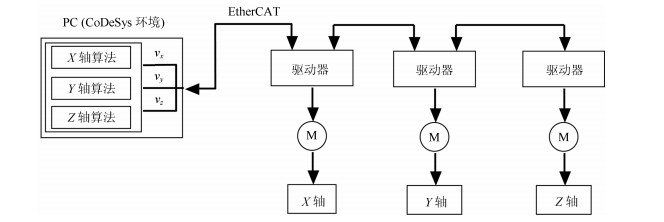
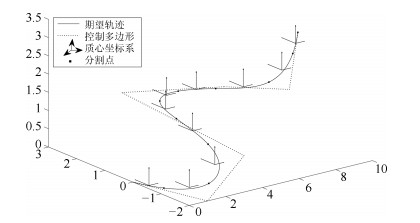
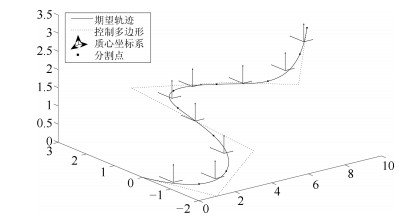
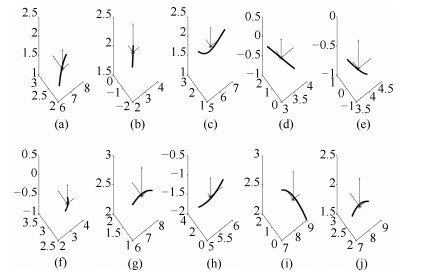
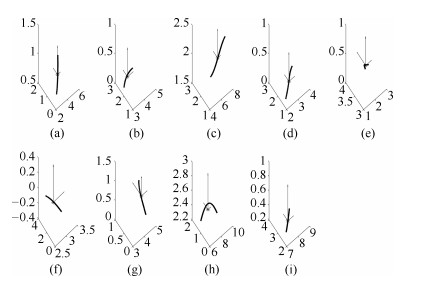
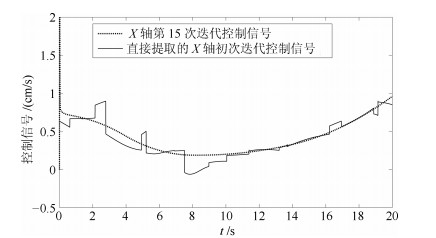
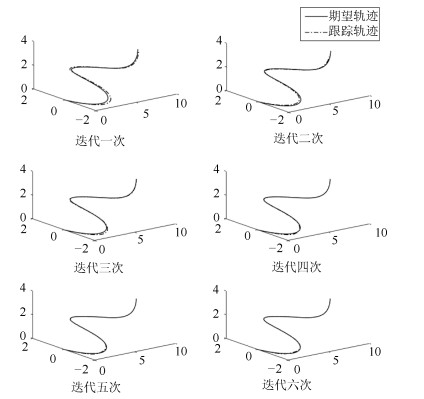
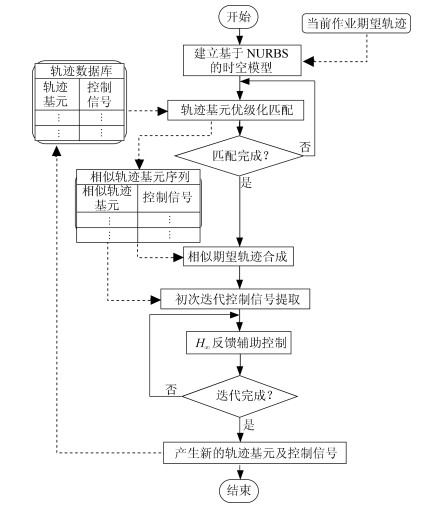
-
摘要: 在同一迭代学习控制(Iterative learning control, ILC)系统中, 选取一个合适的初次迭代控制信号相对于从零开始学习达到目标跟踪精度的迭代次数更少.本文针对线性系统研究从历次轨迹跟踪控制信息中通过期望轨迹匹配提取初次迭代控制信号的方法.首先提出了一种轨迹基元优化匹配算法, 在满足一定相似度的情况下, 通过轨迹分割、平移与旋转变换, 在轨迹基元库中寻找与当前期望轨迹叠合的轨迹基元组合轨迹; 进而, 依据线性叠加原理和轨迹叠合的平移矢量与旋转变换矩阵, 获取与期望轨迹叠合的轨迹基元控制信号; 在此基础上, 通过轨迹基元控制信号串联组合和时间尺度变换, 提取出当前期望轨迹的初次迭代控制信号.对于初次迭代控制信号在拼接处由边界条件差异引起的干扰, 给出了一种${H_\infty }$反馈辅助ILC方法.最后, 在$XYZ$三轴运动平台实现所提算法, 实验结果表明本文所提方法的有效性.
-
关键词:
- 迭代学习控制 /
- ${H_\infty }$反馈 /
- 初次迭代控制信号 /
- 优化匹配 /
- 轨迹基元
Abstract: In the same iterative learning control (ILC) system, compared with an iterative process that starts from blind, selecting a proper initial control signal has fewer iterations to achieve the target tracking accuracy. This paper studies the method of extracting the initial iterative control signal from all previous trajectory tracking control information through matching the desired trajectory for linear systems. First, a trajectory primitive optimal matching algorithm is proposed. In the case of a given similarity index, some trajectory primitive combinations superposed on the current desired trajectory are found from the trajectory library through the trajectory segmentation, translation and rotation transformation. Further, according to the linear superposition principle, translation vectors and rotation matrices on superposing trajectory, the control signals of the trajectory primitives superimposed on the desired trajectory are acquired. By assembling the trajectory primitive control signals in series and transforming their time scales, an initial iteration control signal of the current desired trajectory is extracted. For the interference caused by the difference of the boundary condition of the initial iteration control signals at the splicing, an ${H_\infty }$ feedback assistant ILC method is presented. Finally, the proposed algorithm is implemented on the $XYZ$ triaxial motion platform, the experiment results show that the proposed method is effective.-
Key words:
- Iterative learning control /
- ${H_\infty }$ feedback /
- initial iterative control signal /
- optimal matching and combining algorithm /
- trajectory primitives
1) 本文责任编委 侯忠生 -
图 1 轨迹基元匹配的ILC系统原理示意图
Fig. 1 ILC system schematic diagram of trajectory primitive matching
图 3 原始相似组合轨迹基元序列${l^{A}_{p1j}(t_{1j})}, $ ${l^{A}_{p2j}(t_{2j})}$
Fig. 3 Original similar combination of primitive sequences ${l^{A}_{p1j}(t_{1j})}, $ ${l^{A}_{p2j}(t_{2j})}$
图 4 重新分割后的相似组合轨迹基元序列$\bar l_{p1r}^{A}({t_{1r}}), $ $\bar l_{p2r}^{A}({t_{2r}})$
Fig. 4 Re-segmented similar combinations of primitive sequences $\bar l_{p1r}^{A}({t_{1r}}), $ $\bar l_{p2r}^{A}({t_{2r}})$
图 5 ${H_\infty }$反馈辅助迭代学习控制系统
Fig. 5 ${H_\infty }$ feedback assisted iterative learning control system
图 10 分割成十段的期望轨迹及各段质心坐标系
Fig. 10 The desired trajectory split into 10 segments and its centroid coordinates
图 11 分割成九段的期望轨迹及各段质心坐标系
Fig. 11 The desired trajectory split into 9 segments and its centroid coordinates
图 14 $X$轴初次控制信号及第15次迭代控制信号
Fig. 14 $X$ axis initial control signal and 15th iteration control signal
图 15 $Y$轴初次控制信号及第15次迭代控制信号
Fig. 15 $Y$ axis initial control signal and 15th iteration control signal
图 16 $Z$轴初次控制信号及第15次迭代控制信号
Fig. 16 $Z$ axis initial control signal and 15th iteration control signal
图 20 $X$、$Y$、$Z$轴采用提取的初次控制信号的均方根误差
Fig. 20 The RMS of $X$, $Y$, $Z$ axis for ILC using the extracted initial control signal
图 21 初次控制信号为零的$X$、$Y$、$Z$轴的均方根误差
Fig. 21 The RMS of $X$, $Y$, $Z$ axis for ILC using the zero initial control signal
图 22 采用提取的初次控制信号的三维轨迹跟踪效果
Fig. 22 3-D trajectory tracking performances of ILC using the extracted initial control signal
图 23 初次控制信号为零的三维轨迹跟踪效果
Fig. 23 3-D trajectory tracking performances of ILC using the zero initial control signal
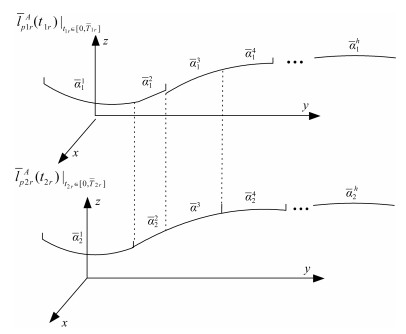
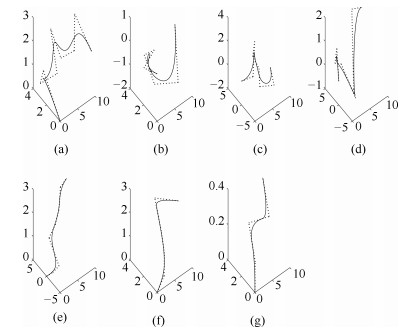
表 1 各基元轨迹段与相应期望轨迹段之间的时间尺度
Table 1 Each primitive corresponding to the desired track segment and a time scale between trajectories segments
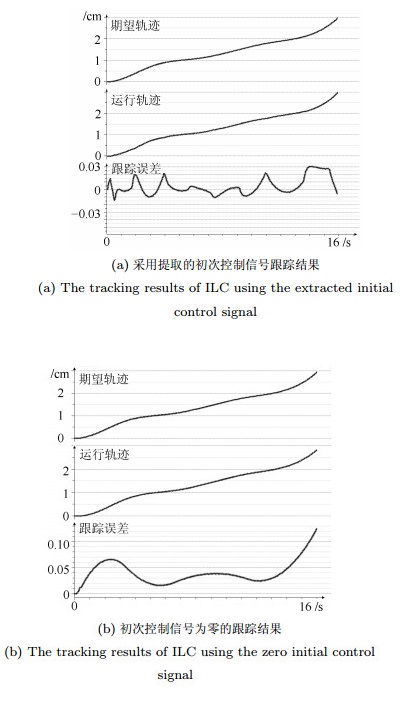
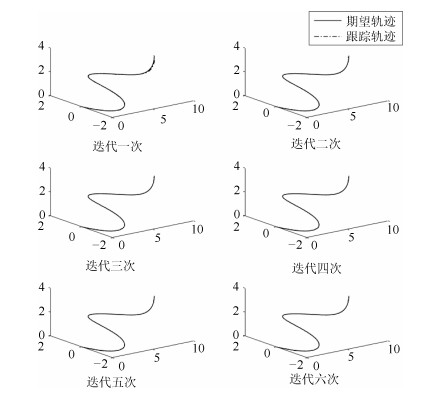
第$r$段 $\overline \alpha _1^{r}$ $\overline \alpha _2^{r}$ 第$r$段 $\overline \alpha _1^{r}$ $\overline \alpha _2^{r}$ 1 1.56 3.76 10 1.24 0.39 2 1.32 3.76 11 1.24 0.36 3 1.32 2.74 12 0.87 0.63 4 1.79 2.74 13 0.87 1.32 5 1.79 2.74 14 0.61 1.32 6 0.99 1.65 15 0.61 1.13 7 0.99 2.16 16 0.91 1.13 8 0.98 2.16 17 0.91 0.89 9 0.98 0.39 18 1.16 0.89 
下载: 导出CSV
表 2 采用提取初次控制信号的跟踪误差
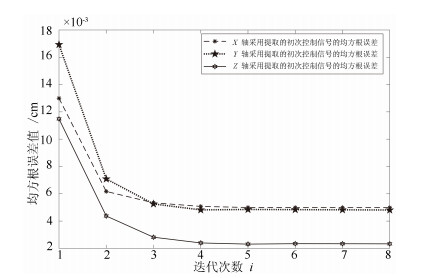
Table 2 The tracking error of ILC using the extracted initial control signal
跟踪指标 $X$轴(mm) $Y$轴(mm) $Z$轴(mm) 最大跟踪误差 0.5211 0.4923 0.4991 第一次迭代均方差 0.1300 0.1692 0.1154 第八次迭代均方差 0.0481 0.0499 0.0233
下载: 导出CSV
表 3 初次控制信号为零的跟踪误差
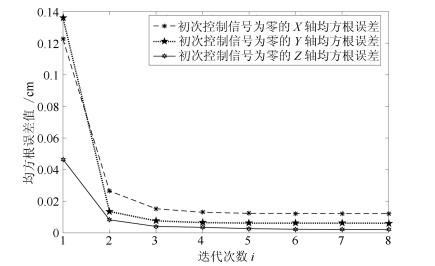
Table 3 The tracking error of ILC using the zero initial control signal
跟踪指标 $X$轴(mm) $Y$轴(mm) $Z$轴(mm) 最大跟踪误差 2.5134 2.0189 1.2174 第一次迭代均方差 1.2260 1.3610 0.4649 第八次迭代均方差 0.1221 0.0614 0.0308
下载: 导出CSV
-
[1] Arimoto S, Kawamura S, Miyazaki F. Bettering operation of robots by learning. Journal of Robotic Systems, 1984, 1(2): 123-140 doi: 10.1002/rob.4620010203 [2] Arif M, Ishihara T, Inooka H. Incorporation of experience in iterative learning controllers using locally weighted learning. Automatica, 2001, 37(6): 881-888 doi: 10.1016/S0005-1098(01)00030-9 [3] Meng D Y, Jia Y M. Effects of initial input on stochastic discrete-time iterative learning control systems. In: Proceedings of the 29th Chinese Control Conference. Beijing, China: IEEE, 2010. 2193-2200 [4] Freeman C T, Alsubaie M A, Cai Z L, Rogers E, Lewin P L. Initial input selection for iterative learning control. Journal of Dynamic Systems Measurement & Control, 2011, 133(5): 054504 [5] Janssens P, Pipeleers G, Swevers J. Initialization of ILC based on a previously learned trajectory. In: Proceedings of the 2012 American Control Conference (ACC). Montreal, QC, Canada: IEEE, 2012. 610-614 [6] Alajmi N, Alobaidly A, Alhajri M, Salamah S, Alsubaie M. An upper limit for iterative learning control initial input construction using singular values. Intelligent Control & Automation, 2017, 8(3): 154-163 [7] Xu J X, Zhu T. Dual-scale direct learning control of trajectory tracking for a class of nonlinear uncertain systems. IEEE Transactions on Automatic Control, 1999, 44(10): 1884-1888 doi: 10.1109/9.793729 [8] Xu J X. Direct learning of control efforts for trajectories with different time scales. IEEE Transactions on Automatic Control, 1998, 43(7): 1027-1030 doi: 10.1109/9.701122 [9] Xu J X. Direct learning of control efforts for trajectories with different magnitude scales. Automatica, 1997, 33(12): 2191-2195 doi: 10.1016/S0005-1098(97)00140-4 [10] Xu J X, Panda S K, Tong H L. Real-time Iterative Learning Control: Design and Applications. London: Springer, 2009. 7-28 [11] Hoelzle D J, Alleyne A G, Johnson A J W. Basis task approach to iterative learning control with applications to micro-robotic deposition. IEEE Transactions on Control Systems Technology, 2011, 19(5): 1138-1148 doi: 10.1109/TCST.2010.2063030 [12] 施法中.计算机辅助几何设计与非均匀有理B样条.第2版.北京:高等教育出版社, 2013. 273-279Shi Fa-Zhong. The CAGD & NURBS Book (Second edition). Beijing: Higher Education Press, 2013. 273-279 [13] Kabsch W. A solution for the best rotation to relate two sets of vectors. Acta Crystallographica Section A, 1976, 32(5): 922-923 doi: 10.1107/S0567739476001873 [14] Umeyama S. Least-squares estimation of transformation parameters between two point patterns. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1991, 13(4): 376-380 -
计量
- 文章访问数: 1829
- HTML全文浏览量: 327
- PDF下载量: 245
- 被引次数: 0
