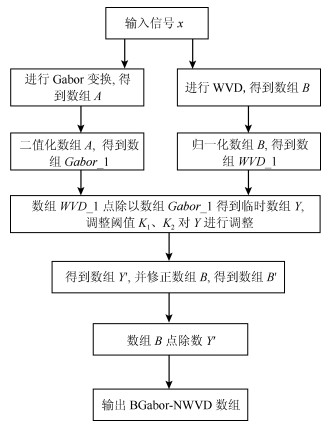
Time-frequency Analysis of BGabor-NSPWVD Algorithm With Strong Robustness and High Sharpening Concentration
-
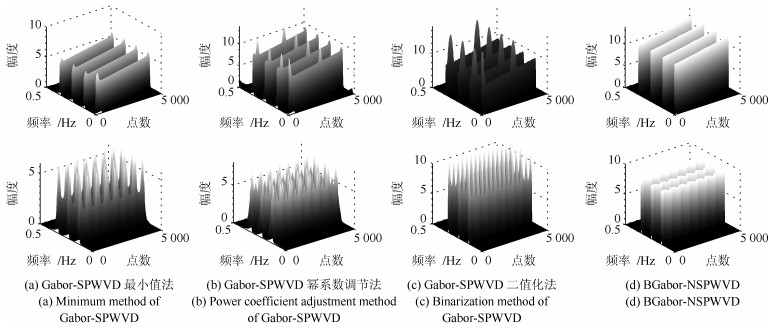
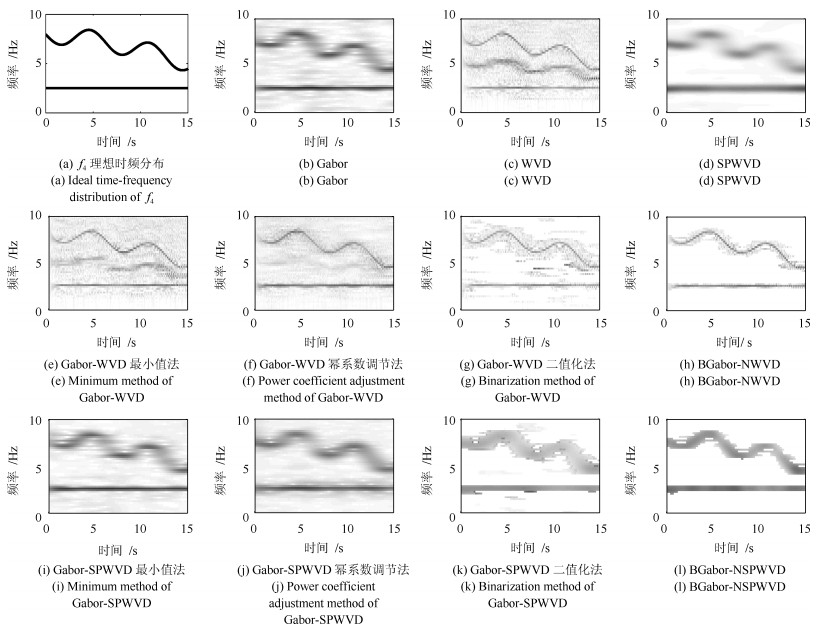
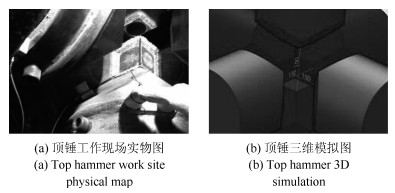
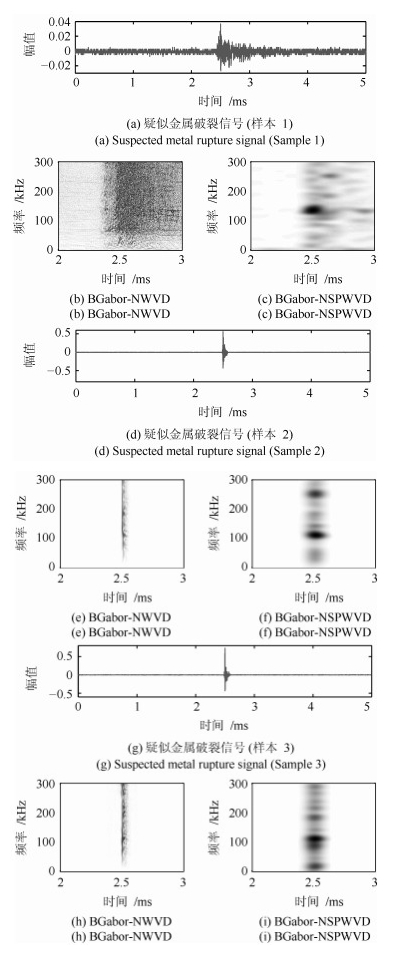
摘要: 针对短时傅里叶变换(Short-time Fourier transform,STFT)、Gabor变换和魏格纳-维尔分布(Wigner-Ville distribution,WVD)出现的时频分辨率模糊和交叉项干扰,以及目前一些主流改进算法如STFT-WVD和Gabor-WVD存在的频率分量三维幅度失真,且抗噪性能及鲁棒性能不理想等问题,提出基于局部二值化、归一化处理再结合的二值化Gabor-归一化WVD(Binarized Gabor-normalized WVD,BGabor-NWVD)和二值化Gabor-归一化伪平滑WVD(Binarized Gabor-normalized smoothed pseudo WVD,BGabor-NSPWVD)算法.数值仿真实验结果表明,BGabor-NWVD和BGabor-NSPWVD算法较好地抑制了交叉项干扰,具有较高的时频锐化聚集度,且两种算法的抗噪性能和鲁棒性也较为理想.基于本文方法对硬质合金顶锤工作时产生的疑似破裂信号进行时频分析,在抑制噪声和交叉项的同时能够较为准确地寻找传感器的频率判别窗口,为金属破裂监测设备数据采集卡提供有效的阈值参考.
-
关键词:
- 时频分析 /
- 交叉项抑制 /
- 鲁棒性 /
- BGabor-NWVD /
- BGabor-NSPWVD
Abstract: For the time-frequency resolution fuzziness and cross-term interference caused by short-time Fourier transform (STFT), Gabor transform and Wigner-Ville distribution (WVD), this paper proposes the binarized Gabor-normalized WVD (BGabor-NWVD) and binarized Gabor-normalized smoothed pseudo WVD (BGabor-NSPWVD) algorithms, which combine partial binaryzation and normalization. Experiment results show that the BGabor-NWVD and BGabor-NSPWVD algorithms can effectively reduce the cross-term interference and have high sharpening resolution of high TF concentration degree. The algorithms can suppress the cross-term, and the anti-noise performance and robustness of the two algorithms are also ideal. Based on the methods, a TF analysis of the suspected rupture signal generated during the work of the carbide torch is carried out to suppress the noise and the cross-term. At the same time, the frequency discrimination window of the sensor can be found accurately, which can be used as threshold reference for the data acquisition board of the metal rupture monitoring equipment.-
Key words:
- Time-frequency analysis /
- cross term inhibition /
- robustness /
- BGabor-NWVD /
- BGabor-NSPWVD
1) 本文责任编委 张俊 -
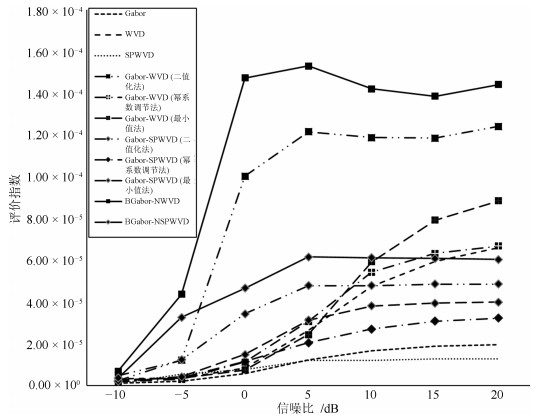
表 1 仿真函数$f_4$在不同噪声条件下各方法的聚集度$E_{JP}$数值比较
Table 1 The $E_{JP}$ numerical comparison of experimental function $f_4$ in different noise conditions
不同方法 SNR = -10 SNR = -5 SNR = 0 SNR = 5 SNR = 10 SNR = 15 SNR = 20 Gabor $9.35\, \times\, 10^{-7}$ $2.03\, \times\, 10^{-6}$ $5.71\, \times\, 10^{-6}$ $1.22\, \times\, 10^{-5}$ $1.65\, \times\, 10^{-5}$ $1.87\, \times\, 10^{-5}$ $1.96\, \times\, 10^{-5}$ WVD $3.10\, \times\, 10^{-6}$ $3.50\, \times\, 10^{-6}$ $8.21\, \times\, 10^{-6}$ $2.62\, \times\, 10^{-5}$ $4.74\, \times\, 10^{-5}$ $5.95\, \times\, 10^{-5}$ $6.59\, \times\, 10^{-5}$ SPWVD $8.35\, \times\, 10^{-7}$ $5.26\, \times\, 10^{-6}$ $7.55\, \times\, 10^{-6}$ $1.18\, \times\, 10^{-5}$ $1.21\, \times\, 10^{-5}$ $1.27\, \times\, 10^{-5}$ $1.27\, \times\, 10^{-5}$ Gabor-WVD (二值化) $4.61\, \times\, 10^{-6}$ $1.21\, \times\, 10^{-5}$ $1.00\, \times\, 10^{-4}$ $1.22\, \times\, 10^{-4}$ $1.19\, \times\, 10^{-4}$ $1.19\, \times\, 10^{-4}$ $1.24\, \times\, 10^{-4}$ Gabor-WVD (幂系数调节) $1.83\, \times\, 10^{-6}$ $2.85\, \times\, 10^{-6}$ $1.12\, \times\, 10^{-5}$ $3.06\, \times\, 10^{-5}$ $5.43\, \times\, 10^{-5}$ $6.33\, \times\, 10^{-5}$ $6.68\, \times\, 10^{-5}$ Gabor-WVD (最小值) $2.76\, \times\, 10^{-6}$ $3.35\, \times\, 10^{-6}$ $7.43\, \times\, 10^{-6}$ $2.43\, \times\, 10^{-5}$ $5.92\, \times\, 10^{-5}$ $7.92\, \times\, 10^{-5}$ $8.85\, \times\, 10^{-5}$ Gabor-SPWVD (二值化) $2.24\, \times\, 10^{-6}$ $1.23\, \times\, 10^{-5}$ $3.43\, \times\, 10^{-5}$ $4.78\, \times\, 10^{-5}$ $4.77\, \times\, 10^{-5}$ $4.85\, \times\, 10^{-5}$ $4.86\, \times\, 10^{-5}$ Gabor-SPWVD (幂系数调节) $1.76\, \times\, 10^{-6}$ $3.75\, \times\, 10^{-6}$ $1.14\, \times\, 10^{-5}$ $2.04\, \times\, 10^{-5}$ $2.70\, \times\, 10^{-5}$ $3.07\, \times\, 10^{-5}$ $3.22\, \times\, 10^{-5}$ Gabor-SPWVD (最小值) $2.02\, \times\, 10^{-6}$ $4.04\, \times\, 10^{-6}$ $1.49\, \times\, 10^{-5}$ $3.13\, \times\, 10^{-5}$ $3.81\, \times\, 10^{-5}$ $3.94\, \times\, 10^{-5}$ $3.99\, \times\, 10^{-5}$ BGabor-NWVD $6.73\, \times\, 10^{-6}$ $4.37\, \times\, 10^{-5}$ $1.47\, \times\, 10^{-4}$ $1.53\, \times\, 10^{-4}$ $1.42\, \times\, 10^{-4}$ $1.39\, \times\, 10^{-4}$ $1.44\, \times\, 10^{-4}$ BGabor-NSPWVD $3.48\, \times\, 10^{-6}$ $3.26\, \times\, 10^{-5}$ $4.66\, \times\, 10^{-5}$ $6.16\, \times\, 10^{-5}$ $6.11\, \times\, 10^{-5}$ $6.08\, \times\, 10^{-5}$ $6.03\, \times\, 10^{-5}$ -
[1] Volaric I, Sucic V, Stankovic S. A data driven compressive sensing approach for time-frequency signal enhancement. Signal Processing, 2017, 141:229-239 doi: 10.1016/j.sigpro.2017.06.013 [2] Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory, 1990, 36(5):961-1005 doi: 10.1109/18.57199 [3] Kayhan A S. Difference equation representation of chirp signals and instantaneous frequency/amplitude estimation. IEEE Transactions on Signal Processing, 1996, 44(12):2948-2958 doi: 10.1109/78.553470 [4] 储昭碧, 张崇巍, 冯小英.基于自适应滤波器的时频分析.自动化学报, 2009, 35(11):1420-1428 http://www.aas.net.cn/CN/abstract/abstract13594.shtmlChu Zhao-Bi, Zhang Chong-Wei, Feng Xiao-Ying. Adaptive filter-based time-frequency analysis. Acta Automatica Sinica, 2009, 35(11):1420-1428 http://www.aas.net.cn/CN/abstract/abstract13594.shtml [5] 杨默涵, 陈万忠, 李明阳.基于总体经验模态分解的多类特征的运动想象脑电识别方法研究.自动化学报, 2017, 43(5):743-752 http://www.aas.net.cn/CN/abstract/abstract19052.shtmlYang Mo-Han, Chen Wan-Zhong, Li Ming-Yang. Multiple feature extraction based on ensemble empirical mode decomposition for motor imagery EEG recognition tasks. Acta Automatica Sinica, 2017, 43(5):743-752 http://www.aas.net.cn/CN/abstract/abstract19052.shtml [6] Cohen L. Time-frequency distributions-a review. Proceedings of the IEEE, 1989, 77(7):941-981 doi: 10.1109/5.30749 [7] Gabor D. Theory of communication. Journal of the Institution of Electrical Engineers, 1946, 93:429-549 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_20930838401474143ef29e11d60c01a5 [8] Mansinha L, Stockwell R G, Lowe R P. Pattern analysis with two-dimensional spectral localisation:applications of two-dimensional S transforms. Physica A:Statistical Mechanics and Its Applications, 1997, 239(1-3):286-295 doi: 10.1016/S0378-4371(96)00487-6 [9] Daubechies I. Ten Lectures on Wavelets. Philadelphia, Pa, USA:SIAM, 1992. 39-72 [10] Huang N E, Shen Z, Long S R, Wu M C, Shih H H, Zheng Q, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971):903-995 doi: 10.1098/rspa.1998.0193 [11] Wu Z H, Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method. Advances in Adaptive Data Analysis, 2011, 1(1):1-41 http://d.old.wanfangdata.com.cn/Periodical/dianzixb201305033 [12] Zhang J, Yan R Q, Gao R X, Feng Z H. Performance enhancement of ensemble empirical mode decomposition. Mechanical Systems and Signal Processing, 2010, 24(7):2104-2123 doi: 10.1016/j.ymssp.2010.03.003 [13] Daubechies I, Lu J F, Wu H T. Synchrosqueezed wavelet transforms:an empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, 2011, 30(2):243-261 doi: 10.1016/j.acha.2010.08.002 [14] Zhou W X, Shao Z F, Diao C Y, Cheng Q M. High-resolution remote-sensing imagery retrieval using sparse features by auto-encoder. Remote Sensing Letters, 2015, 6(10):775-783 doi: 10.1080/2150704X.2015.1074756 [15] Boashash B, Black P. An efficient real-time implementation of the Wigner-Ville distribution. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(11):1611-1618 doi: 10.1109/TASSP.1987.1165070 [16] 王见, 李金同, 卢华玲, 尹爱军.采用STFT-Wigner变换抑制Wigner-Ville分布交叉项.重庆大学学报, 2013, 36(8) 15-18, 25 http://d.old.wanfangdata.com.cn/Periodical/cqdxxb201308003Wang Jian, Li Jin-Tong, Lu Hua-Ling, Yin Ai-Jun. Using STFT-Wigner transform to suppress the cross terms in Wigner-Ville distribution. Journal of Chongqing University, 2013, 36(8) 15-18, 25 http://d.old.wanfangdata.com.cn/Periodical/cqdxxb201308003 [17] 付卫红, 王璐, 贾坤, 路贵朝.基于STFT与SPWVD的跳频参数盲估计算法.华中科技大学学报(自然科学版), 2014, 42(9):59-63 http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201409013Fu Wei-Hong, Wang Lu, Jia Kun, Lu Gui-Chao. Blind parameter estimation algorithm for frequency hopping signals based on STFT and SPWVD. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(9):59-63 http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201409013 [18] 郝国成, 陈忠昌, 赵娟, 曾佐勋, 刘辉, Sibgatulin V G, 等.基于NSTFT-WVD变换的芦山slMs7.0级地震前后地球天然脉冲电磁场信号时频分析.地学前缘, 2016, 23(1) 276-286Hao Guo-Cheng, Chen Zhong-Chang, Zhao Juan, Zeng Zuo-Xun, Liu Hui, Sibgatulin V G, et al. Time-frequency analysis of the Earth's natural pulse electromagnetic field signal before and after the Lushan slMs7.0 earthquake based on NSTFT-WVD transform. Earth Science Frontiers, 2016, 23(1) 276-286 [19] Zhou J, Fang X Y, Tao L. A sparse analysis window for discrete Gabor transform. Circuits, Systems, and Signal Processing, 2017, 36(10):4161-4180 doi: 10.1007/s00034-017-0510-0 [20] Jones D L, Parks T W. A high resolution data-adaptive time-frequency representation. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(12):2127-2135 doi: 10.1109/29.61539 [21] Allen J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1977, 25(3):235-238 doi: 10.1109/TASSP.1977.1162950 [22] 王民, 王松顺.硬质合金顶锤和压缸的破裂特征、破坏因素的分析和提高使用寿命的途径.硬质合金, 1994, 11(4):231-240 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199400560973Wang Min, Wang Song-Shun. The breakage characteristic and breakdown factors analysis of cemented carbide anvil and pressure die and the way of raise their sevice life. Gemented Carbide, 1994, 11(4):231-240 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199400560973 [23] Ibrahim M E, Zhuang W Z L. Nondestructive inspection of fatigue crack propagation beneath supersonic particle deposition coatings during fatigue testing. International Journal of Fatigue, 2017, 102:149-157 doi: 10.1016/j.ijfatigue.2017.05.005 -




 下载:
下载: