A Semi-supervised Clustering Algorithm Based on Factor Graph Model for Dynamic Graphs
-
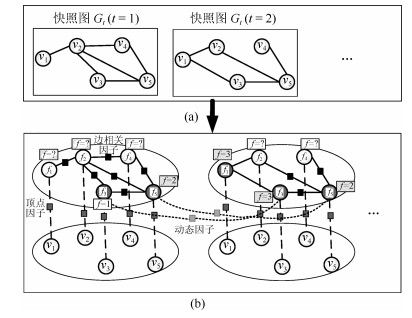
摘要: 针对动态图的聚类主要存在着两点不足:首先, 现有的经典聚类算法大多从静态图分析的角度出发, 无法对真实网络图持续演化的特性进行有效建模, 亟待对动态图的聚类算法展开研究, 通过对不同时刻图快照的聚类结构进行分析进而掌握图的动态演化情况.其次, 真实网络中可以预先获取图中部分节点的聚类标签, 如何将这些先验信息融入到动态图的聚类结构划分中, 从而向图中的未标记节点分配聚类标签也是本文需要解决的问题.为此, 本文提出进化因子图模型(Evolution factor graph model, EFGM)用于解决动态图节点的半监督聚类问题, 所提EFGM不仅可以捕获动态图的节点属性和边邻接属性, 还可以捕获节点的时间快照信息.本文对真实数据集进行实验验证, 实验结果表明EFGM算法将动态图与先验信息融合到一个统一的进化因子图框架中, 既使得聚类结果满足先验知识, 又契合动态图的整体演化规律, 有效验证了本文方法的有效性.Abstract: There are two main deficiencies on clustering of dynamic graphs. Firstly, most of existing classical algorithms analyze such graphs from the perspective of static analysis. However, static analysis is not capable of modeling the continuous evolution of real-world networks. Therefore, it is a great need to research on clustering algorithms for dynamic graphs. Our goal is to capture the dynamic evolution characteristics by considering the clustering structure of multiple snapshots as a whole. Secondly, some clustering labels of some nodes in real-world graphs can be obtained in advance, thus how to integrate these priori information into clustering assignments of dynamic graphs and assign clustering labels to the unlabeled nodes of each snapshot should be resolved. In this paper, we propose an evolution factor graph model (EFGM) for the semi-supervised clustering of nodes in dynamic networks. EFGM is able to capture the node-attribute and edge-adjacency attribute of each node of the dynamic graphs, and also make full use of the snapshot information. We experiment with the real-world graphs and experimental results show that the EFGM integrates the prior knowledge and the dynamic graph into a unified framework (i.e., evolution factor graph model), which makes the clustering result satisfy the prior label information and conform to the overall evolution of dynamic graphs. It validates the effectiveness of the proposed approach.
-
Key words:
- Semi-supervised clustering /
- evolution factor graph model (EFGM) /
- feature extraction /
- dynamic graphs
1) 本文责任编委 朱军 -
表 1 相关符号说明
Table 1 Description of symbols
符号 说明 $G_L $ 部分标注网络 $V_L $ 被标注的节点 $V_U $ 未被标注的节点 $E$ 图中的边集合 $W$ $W_{ij} $为节点$V_i $的第$j_{th} $个属性值 $f$ 映射函数, 将每个节点$i$赋予相应的标签, 记为$f_i$ $\Omega $ 部分标注动态网络 表 2 DBLP数据集的会议名称和聚类簇标签
Table 2 Conference names and their clustering labels of DBLP dataset
聚类簇标签 会议名称 AI & ML IJCAI, AAAI, ICML, UAI, AISTATS AL & TH FOCS, STOC, SODA, COLT CV CVPR, ICCV, ECCV, BMVC DB EDBT, ICDE, PODS, SIGMOD, VLDB DM KDD, SDM, ICDM, PAKDD IR SIGIR, ECIR 表 3 DBLP会议论文网络的统计信息
Table 3 Statistics of DBLP conference network
年份 作者关系 关系数量 2001 3 074 5 743 2002 2 557 5 343 2003 3 836 7 700 2004 3 464 7 132 2005 5 198 11 171 2006 4 494 9 392 2007 7 294 15 708 2008 5 780 12 398 2009 6 405 14 321 2010 5 757 12 738 表 4 真实网络图的实验结果比较
Table 4 Comparison of results on real-world graphs
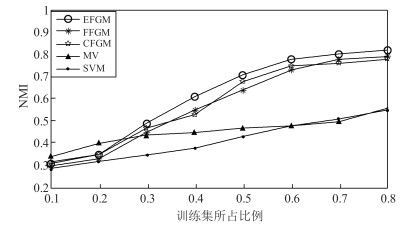
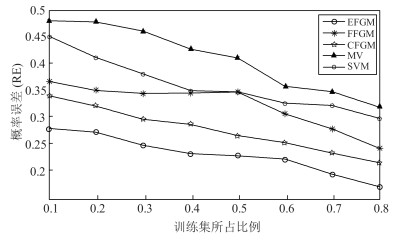
网络集 相应算法 NMI RE HEPCitation EFGM 0.845 0.203 FFGM 0.393 0.478 CFGM 0.824 0.245 MV 0.578 0.450 SVM 0.502 0.423 DBLP EFGM 0.885 0.196 FFGM 0.493 0.280 CFGM 0.814 0.235 MV 0.678 0.350 SVM 0.560 0.323 表 5 各个算法在真实网络数据集上的处理时间比较(秒)
Table 5 Comparison of the execution time on a real-world networks (s)
运行时间(s) EFGM FFGM CFGM MV SVM HEPCitation 282.8 269.2 272.6 220.3 394.4 DBLP 123.8 110.3 108.2 84 232.3 表 6 不同特征提取方法的实验结果比较
Table 6 Comparison of results on different feature extraction methods
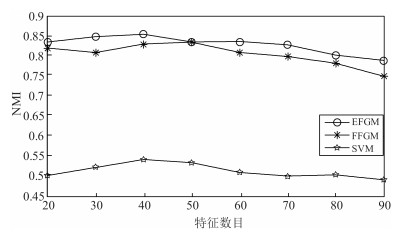
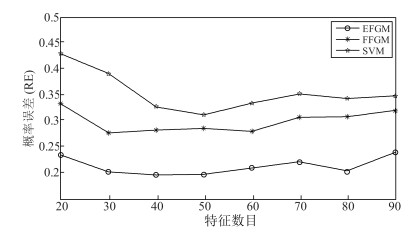
特征提取方法 NMI RE ReFeX EFGM 0.837 0.222 FFGM 0.372 0.427 CFGM 0.799 0.253 Node2vec EFGM 0.852 0.193 FFGM 0.402 0.392 CFGM 0.819 0.235 -
[1] 黄立威, 李彩萍, 张海粟, 刘玉超, 李德毅, 刘艳博.一种基于因子图模型的半监督社区发现方法.自动化学报, 2016, 42(10): 1520-1531 doi: 10.16383/j.aas.2016.c150261Huang Li-Wei, Li Cai-Ping, Zhang Hai-Su, Liu Yu-Chao, Li De-Yi, Liu Yan-Bo. A semi-supervised community detection method based on factor graph model. Acta Automatica Sinica, 2016, 42(10): 1520-1531 doi: 10.16383/j.aas.2016.c150261 [2] Girvan M, Newman M E J. Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826 doi: 10.1073/pnas.122653799 [3] Newman M E J. Fast algorithm for detecting community structure in networks. Physical Review E, 2004, 69(6): Article No. 066133 http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cond-mat%2f0309508 [4] Raghavan U N, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks. Physical Review E, 2007, 76(3): Article No. 036106 http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0709.2938 [5] Chakrabarti D, Kumar R, Tomkins A. Evolutionary clustering. In: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Philadelphia, PA, USA: ACM, 2006. 554-560 http://www.researchgate.net/publication/221654105_Evolutionary_clustering [6] Pan S R, Zhu X Q, Zhang C Q, Yu P S. Graph stream classification using labeled and unlabeled graphs. In: Proceedings of the IEEE 29th International Conference on Data Engineering (ICDE). Brisbane, QLD, Australia: IEEE, 2013. 398-409 http://www.researchgate.net/publication/261345341_Graph_stream_classification_using_labeled_and_unlabeled_graphs [7] Zhao Y C, Wang G, Yu P S, Liu S B, Zhang S. Inferring social roles and statuses in social networks. In: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago, USA: ACM, 2013. 695-703 http://www.researchgate.net/publication/266654052_Inferring_social_roles_and_statuses_in_social_networks [8] Choobdar S, Ribeiro P, Parthasarathy S, Silva F. Dynamic inference of social roles in information cascades. Data Mining and Knowledge Discovery, 2015, 29(5): 1152-1177 doi: 10.1007/s10618-015-0402-5 [9] Grover A, Leskovec J. Node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, California, USA: ACM, 2016. 855-864 https://www.researchgate.net/publication/305997704_node2vec_Scalable_Feature_Learning_for_Networks [10] 常振超.在线社会网络社团检测关键技术研究[博士学位论文], 解放军信息工程大学, 中国, 2016Chang Zhen-Chao. Research on Key Technologies of Community Detection in Online Social Networks[Ph.D. dissertation], Information Engineering University, China, 2016 [11] Lin Y R, Chi Y, Zhu S, Sundaram H, Tseng B L. Analyzing communities and their evolutions in dynamic social networks. ACM Transactions on Knowledge Discovery from Data (TKDD), 2009, 3(2): Article No. 8 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=WFHYXW320184 [12] Chi Y, Song X D, Zhou D Y, Hino K, Tseng B L. Evolutionary spectral clustering by incorporating temporal smoothness. In: Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose, California, USA: ACM, 2007. 153-162 [13] Dinh T N, Nguyen N P, Thai M T. An adaptive approximation algorithm for community detection in dynamic scale-free networks. In: Proceedings of the 2013 IEEE International Conference on Computer Communications. Turin, Italy: IEEE, 2013. 55-59 http://www.researchgate.net/publication/261462402_An_adaptive_approximation_algorithm_for_community_detection_in_dynamic_scale-free_networks [14] Sun J M, Faloutsos C, Papadimitriou S, Yu P S. Graphscope: parameter-free mining of large time-evolving graphs. In: Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose, California, USA: ACM, 2007. 687-696 http://www.researchgate.net/publication/221654321_GraphScope_parameter-free_mining_of_large_time-evolving_graphs [15] 肖杰斌, 张绍武.基于随机游走和增量相关节点的动态网络社团挖掘算法.电子与信息学报, 2013, 35(4): 977-981 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkxxk201304036Xiao Jie-Bin, Zhang Shao-Wu. An algorithm of integrating random walk and increment correlative vertexes for mining community of dynamic networks. Journal of Electronics & Information Technology, 2013, 35(4): 977-981 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkxxk201304036 [16] Ning H Z, Xu W, Chi Y, Gong Y H, Huang T S. Incremental spectral clustering by efficiently updating the eigen-system. Pattern Recognition, 2010, 43(1): 113-127 http://cn.bing.com/academic/profile?id=46240821097459119fa011826a06c99a&encoded=0&v=paper_preview&mkt=zh-cn [17] Ma X K, Gao L, Yong X R, Fu L D. Semi-supervised clustering algorithm for community structure detection in complex networks. Physica A: Statistical Mechanics and its Applications, 2010, 389(1): 187-197 doi: 10.1016/j.physa.2009.09.018 [18] Allahverdyan A E, Ver Steeg G, Galstyan A. Community detection with and without prior information. EPL (Europhysics Letters), 2010, 90(1): Article No. 18002 doi: 10.1209/0295-5075/90/18002 [19] Eaton E, Mansbach R. A spin-glass model for semi-supervised community detection. In: Proceedings of the 26th AAAI Conference on Artificial Intelligence. Toronto, Ontario, Canada: AAAI, 2012. 900-906 https://www.researchgate.net/publication/268350911_A_Spin-Glass_Model_for_Semi-Supervised_Community_Detection [20] Liu D, Liu X, Wang W J, Bai H Y. Semi-supervised community detection based on discrete potential theory. Physica A: Statistical Mechanics and its Applications, 2014, 416: 173-182 doi: 10.1016/j.physa.2014.08.051 [21] Yang L, Cao X C, Jin D, Wang X, Meng D. A unified semi-supervised community detection framework using latent space graph regularization. IEEE Transactions on Cybernetics, 2015, 45(10): 2585-2598 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=05d1e8c05c606c057da50daac18de1a3 [22] Li L, Du M, Liu G, Hu X G, Wu G Q. Extremal optimization-based semi-supervised algorithm with conflict pairwise constraints for community detection. In: Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). Beijing, China: IEEE, 2014. 180-187 http://www.researchgate.net/publication/286758921_Extremal_optimization-based_semi-supervised_algorithm_with_conflict_pairwise_constraints_for_community_detection [23] Li K, Guo S X, Du N, Gao J, Zhang A D. Learning, analyzing and predicting object roles on dynamic networks. In: Proceedings of IEEE 13th International Conference on Data Mining (ICDM). Dallas, TX, USA: IEEE, 2013. 428-437 http://www.researchgate.net/publication/269033111_Learning_Analyzing_and_Predicting_Object_Roles_on_Dynamic_Networks [24] Yao Y B, Holder L. Scalable SVM-based classification in dynamic graphs. In: Proceedings of the 2014 IEEE International Conference on Data Mining (ICDM). Shenzhen, China: IEEE, 2014. 650-659 http://www.researchgate.net/publication/282237894_Scalable_SVM-Based_Classification_in_Dynamic_Graphs?ev=auth_pub [25] Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. Cambridge: MIT Press, 2009. [26] Tang W B, Zhuang H L, Tang J. Learning to infer social ties in large networks. In: Proceeding of the 2011 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Heidelberg: Springer, 2011. 381-397 [27] Yang Z, Tang J, Li J Z, Yang W J. Social community analysis via a factor graph model. IEEE Intelligent Systems, 2011, 26(3): 58-65 doi: 10.1109/MIS.2010.55 [28] Xu H, Yang Y J, Wang L W, Liu W H. Node classification in social network via a factor graph model. In: Proceedings of the 2013 Pacific-Asia Conference on Knowledge Discovery and Data Mining. Berlin, Heidelberg: Springer, 2013. 213-224 https://www.researchgate.net/publication/273204869_Node_Classification_in_Social_Network_via_a_Factor_Graph_Model [29] Murphy K P, Weiss Y, Jordan M I. Loopy belief propagation for approximate inference: An empirical study. In: Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence. Stockholm, Sweden: Morgan Kaufmann Publishers Inc., 1999. 467-475 http://www.researchgate.net/publication/235356658_Loopy_Belief [30] Mao Q, Wang L, Tsang I W, Sun Y J. Principal graph and structure learning based on reversed graph embedding. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(11): 2227-2241 doi: 10.1109/TPAMI.2016.2635657 [31] Chen S H, Niu S F, Akoglu L, Kovačević J, Faloutsos C. Fast, Warped Graph Embedding: Unifying Framework and One-Click Algorithm. arXiv preprint arXiv: 1702.05764, 2017. [32] Shijia E, Jia S B, Xiang Y, Ji Z L. Knowledge graph embedding for link prediction and triplet classification. In: Proceedings of the 2016 Knowledge Graph and Semantic Computing: Semantic, Knowledge, and Linked Big Data. Singapore: Springer, 2016. 228-232 https://www.researchgate.net/publication/310742316_Knowledge_Graph_Embedding_for_Link_Prediction_and_Triplet_Classification [33] Hu W M, Gao J, Xing J L, Zhang C, Maybank S. Semi-supervised tensor-based graph embedding learning and its application to visual discriminant tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(1): 172-188 doi: 10.1109/TPAMI.2016.2539944 [34] Lueckenga J, Engel D, Green R. Weighted vote algorithm combination technique for anomaly based smart grid intrusion detection systems. In: Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN). Vancouver, BC, Canada: IEEE, 2016. 2738-2742 Weighted vote algorithm combination technique for anomaly based smart grid intrusion detection systems -




 下载:
下载: