-
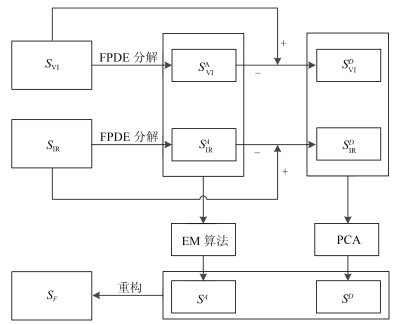
摘要: 针对传统红外与可见光图像融合算法中存在的细节信息不够丰富, 边缘信息保留不够充分等问题, 文中提出了一种基于四阶偏微分方程(Fourth-order partial differential equation, FPDE)的改进的图像融合算法.算法首先采用FPDE将已配准的红外与可见光图像进行分解, 得到高频分量和低频分量; 然后, 对高频分量采用基于主成分分析(Principal component analysis, PCA)的融合规则来得到细节图像, 对低频分量采用基于期望值最大(Expectation maximization, EM)的融合规则来得到近似图像; 最后, 通过组合最终的高频分量和低频分量来重构得到最终的融合结果.实验是建立在标准的融合数据集上进行的, 并与传统的和最近的融合方法进行比较, 结果证明所提方法得到的融合图像比现有的融合方法能有效地综合红外与可见光图像中的重要信息, 有更好的视觉效果.Abstract: Aiming at the problems that the traditional infrared and visible light image fusion algorithms are not rich enough in detail, and the edge information is not sufficiently reserved, an improved image fusion algorithm based on the fourth-order partial differential equation (FPDE) is proposed. The algorithm firstly decomposes the registered infrared and visible images with FPDE to get the high frequency and low frequency components, and then uses the principal component analysis (PCA) fusion rules for the high frequency components to obtain the detail image. An approximation image is obtained using the fusion rule based on the expectation maximization (EM) for low frequency components; Finally, by combining the final high-frequency components and low frequency components to reconstruct the final fusion results. The experiment is based on a standard fusion dataset and compared with the traditional and recent fusion methods. The results show that the proposed fusion method can effectively integrate the important information of infrared and visible images, better visual effects.
-
Key words:
- Image fusion /
- fourth-order partial differential equation(FPDE) /
- expectation maximization (EM) /
- principal component analysis(PCA) /
- infrared and visible images
1) 本文责任编委 黄庆明 -
表 1 "dune"的融合结果的客观指标评价结果
Table 1 Objective evaluation result of the fusion result of "dune"
融合方法 MI IE SD EIPV GRAD 1.2948 4.9 37.9309 0.4278 RATIO 0.7248 4.2485 18.5883 0.3546 DWT 0.6542 4.3821 21.0136 0.3841 FPDE 0.7339 4.2997 19.6550 0.4821 CVT-SR 1.5809 4.8953 38.4630 0.4408 VSM 0.7053 4.3278 20.1876 0.4085 本文方法 2.4647 5.0006 41.2892 0.5106 表 2 "pavilion"的融合结果的客观指标评价结果
Table 2 Objective evaluation result of the fusion result of "pavilion"
融合方法 MI IE SD EIPV GRAD 1.9984 4.4074 26.9211 0.4625 RATIO 1.2350 4.4073 25.5996 0.3724 DWT 1.1351 4.4671 28.2542 0.4197 FPDE 1.3621 4.3829 25.8059 0.3846 CVT-SR 1.3812 5.2110 48.8611 0.4251 VSM 1.2409 4.4436 27.8868 0.4451 本文方法 3.1240 4.8207 59.5605 0.4671 表 3 "maninhuis"的融合结果的客观指标评价结果
Table 3 Objective evaluation result of the fusion result of "maninhuis"
融合方法 MI IE SD EIPV GRAD 1.6169 4.7116 28.0854 0.4814 RATIO 0.9408 4.6744 26.7289 0.3857 DWT 0.9312 4.7941 30.4888 0.4371 FPDE 1.0689 4.7081 27.4131 0.4516 CVT-SR 1.3302 5.151 46.7314 0.5015 VSM 1.0296 4.760 29.3688 0.4921 本文方法 3.2612 5.036 57.1928 0.5091 表 4 "UN Camp"的融合结果的客观指标评价结果
Table 4 Objective evaluation result of the fusion result of "UN Camp"
融合方法 MI IE SD EIPV GRAD 1.3059 4.8571 36.0841 0.3918 RATIO 1.0455 4.3359 22.9454 0.3895 DWT 1.0314 4.4535 24.9950 0.3641 FPDE 1.0894 4.3503 22.9777 0.4234 CVT-SR 1.1538 4.7549 32.5279 0.3635 VSM 1.0753 4.3991 23.9920 0.4064 本文方法 2.5529 4.9069 41.5711 0.4461 表 5 其他6组图像客观评价结果
Table 5 Objective evaluation result of the other six groups of images
融合方法 GRAD RATIO DWT FPDE CVT-SR VSM 本文方法 MI 1.9322 1.3495 1.2301 1.3235 1.4803 1.3201 2.9112 IE 4.9659 4.3952 4.4904 4.4409 4.8827 4.4594 4.9711 SD 49.5321 23.9142 25.5283 24.3822 41.2654 26.6849 51.8051 EIPV 0.4732 0.3491 0.4651 0.5244 0.4653 0.4857 0.5276 表 6 各种融合方法的计算时间对比
Table 6 Computational time comparison of different fusion methods
融合方法 GRAD RATIO DWT FPDE CVT-SR VSM 本文方法 时间(s) 2.7914 0.6909 1.6567 8.1072 5.4289 5.6316 71.7869 -
[1] 童涛, 杨桄, 孟强强, 孙嘉成, 叶怡, 陈晓榕.基于边缘特征的多传感器图像融合算法.红外与激光工程, 2014, 43(1): 311-317 doi: 10.3969/j.issn.1007-2276.2014.01.055Tong Tao, Yang Guang, Meng Qiang-Qiang, Sun Jia-Cheng, Ye Yi, Chen Xiao-Rong. Multi-sensor image fusion algorithm based on edge feature. Infrared and Laser Engineering, 2014, 43(1): 311-317 doi: 10.3969/j.issn.1007-2276.2014.01.055 [2] Li Shu-Tao, Kang Xu-Dong, Fang Le-Yuan, Hu Jian-Wen, Yin Hai-Tao. Pixel-level image fusion: A survey of the state of the art. Information Fusion, 2017, 33(1): 100-112 [3] Zhang Qiong, Maldague Xavier. An adaptive fusion approach for infrared and visible images based on NSCT and compressed sensing. Infrared Physics and Technology, 2016, 74(1): 11-20 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0b634893125f83498d0b8613c8c9ec69 [4] Lee M W, Kwak K C. Performance Comparison of Infrared and Visible Image Fusion Approaches. In: Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), Prague, Czech Republic: 2017. 274-277 [5] Burt P J, Adelson E H.The Laplacian pyramid as a compact image code. IEEE Transactions on Communications, 1983, 31(4): 532-540 doi: 10.1109/TCOM.1983.1095851 [6] 肖进胜, 饶天宇, 贾茜, 宋金钟, 易本顺.基于图切割的拉普拉斯金字塔图像融合算法.光电子·激光, 2014, 25(07): 1416-1424 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdzjg201407032Xiao Jin-Sheng, Rao Tian-Yu, Jia Qian, Song Jin-Zhong, Yi Ben-Shun. An image fusion algorithm of Laplacian pyramid based on graph cuting. Journal of Optoelectronics·Laser, 2014, 25(07): 1416-1424 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdzjg201407032 [7] Burt P J, A gradient pyramid basis for pattern-selective image fusion, In: Proceedings of the SID International Symposium. New York, USA: 1992. 467-470 [8] Alexander Toet, Image fusion by a ratio of low-pass pyramid. Pattern Recognition Letters, 1989, 9(4): 245-253 doi: 10.1016/0167-8655(89)90003-2 [9] 李建林, 俞建成, 孙胜利.基于梯度金字塔图像融合的研究.科学技术与工程, 2007, 7(22): 5818-5822 doi: 10.3969/j.issn.1671-1815.2007.22.018Li Jian-Lin, Yu Jian-Cheng, Sun Sheng-Li. Research on image fusion based on gradient pyramid. Science Technology and Engineering, 2007, 7(22): 5818-5822 doi: 10.3969/j.issn.1671-1815.2007.22.018 [10] Xiang Yan, Qin Han-Lin, Li Jia, Zhou Hui-Xin, Zong Jing-Guo. Infrared and visible image fusion with spectral graph wavelet transform. Journal of the Optical Society of America A Optics Image Science & Vision, 2015, 32(9): 1643-1652 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0da6606f5b60ddc886110a710f7e7b12 [11] Pal C, Das P, Chakrabarti A, Ghosh R. Rician noise removal in magnitude MRI images using efficient anisotropic diffusion filtering. International Journal of Imaging Systems and Technology, 2017, 27(3): 248-264 doi: 10.1002/ima.22230 [12] 钱伟新, 刘瑞根, 王婉丽, 祁双喜, 王伟, 程晋明.基于图像特征方向的各向异性扩散滤波方法.中国图象图形学报, 2006, 11(6): 818-822 doi: 10.3969/j.issn.1006-8961.2006.06.008Qian Wei-Xin, Liu Rui-Gen, Wang Wan-Li, Qi Shuang-Xi, Wang Wei, Cheng Jin-Ming. The anisotropic diffusion methods based on the directions of the image feature. Journal of Image and Graphics, 2006, 11(6): 818-822 doi: 10.3969/j.issn.1006-8961.2006.06.008 [13] You Yu-Li, Kaveh M. Fourth-order partial differential equations for noise removal. IEEE Transactions on Image Processing, 2000, 9(10): 1723-1730 doi: 10.1109/83.869184 [14] Bavirisetti D P, Xiao G, Liu G. Multi-sensor image fusion based on fourth order partial differential equations. International Conference on Information Fusion. Xi'an, China: IEEE, 2017. 1-9 [15] Strang G. Introduction to Applied Mathematic, New York, Wellesley-Cambridge. Springer, 1986. 166-179 [16] Himanshi, Bhateja V, Krishn A, Sahu A. An improved medical image fusion approach using PCA and complex wavelets. In: Proceedings of International Conference on Medical Imaging, M-Health and Emerging Communication Systems, Greater Noida, India: IEEE, 2015. 442-447 [17] Yang J, Blum R S. A statistical signal processing approach to image fusion for concealed weapon detection. In: Proc- eedings of the 2002 International Conference on Image Processing, New York, USA: IEEE, 2002. 513-516 [18] TNO Image Fusion Dataset[Online], available: https://figshare.com/articles/TNO_Image_Fusion_Dataset/1008029, September 15, 2018 [19] Kadar I. Pixel-level image fusion: the case of image sequences. In: Proceedings of SPIE-The International Society for Optical Engineering, 1998, 3374: 378-388 [20] Ma Jin-Lei, Zhou Zhi-Qiang, Wang Bo, Zong Hua. Infrared and visible image fusion based on visual saliency map and weighted least square optimization. Infrared Physics & Technology, 2017, 82: 8-17 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0cf016ce28d21ceabc85edf6d555f29c [21] Liu Yu, Liu Shu-Ping, Wang Zeng-Fu. A general framework for image fusion based on multi-scale transform and sparse representation. Information Fusion, 2015, 24: 147-164 doi: 10.1016/j.inffus.2014.09.004 [22] 张小利, 李雄飞, 李军.融合图像质量评价指标的相关性分析及性能评估.自动化学报, 2014, 40(2): 306-315 doi: 10.3724/SP.J.1004.2014.00306Zhang Xiao-Li, Li Xiong-Fei, Li Jun. Validation and correlation analysis of metrics for evaluating performance of image fusion. Acta Automatica Sinica, 2014, 40(2): 306-315 doi: 10.3724/SP.J.1004.2014.00306 -




 下载:
下载: