基于改进Smith预估控制结构的二自由度PID控制

尹成强; 高洁; 孙群; 赵颖

doi:10.16383/j.aas.2018.c170596

基于改进Smith预估控制结构的二自由度PID控制

doi: 10.16383/j.aas.2018.c170596

尹成强^1, ,,
高洁^1,,
孙群^1,,
赵颖^1,

1.
聊城大学机械与汽车工程学院聊城 252059

基金项目:

国家自然科学基金 61703192

山东省重点研发计划 2016GNC112014

山东省高等学校科技计划 J15LB09

详细信息

作者简介:
高洁  聊城大学机械与汽车工程学院副教授.主要研究方向为交通控制与交通规划. E-mail: gaojie7983@163.com

孙群  聊城大学机械与汽车工程学院教授.主要研究方向为机器人技术, 测量与控制. E-mail: sunxiaoqun97@163.com

赵颖  聊城大学机械与汽车工程学院教授.主要研究方向为机器视觉, 机器人技术. E-mail: zhaoying@lcu.edu.cn

通讯作者:
尹成强聊城大学机械与汽车工程学院副教授.主要研究方向为过程控制与计算机控制.本文通信作者.E-mail: shtjycq@163.com

计量
- 文章访问数: 1366
- HTML全文浏览量: 242
- PDF下载量: 279
- 被引次数: 0
出版历程
- 收稿日期: 2017-10-26
- 录用日期: 2018-03-16
- 刊出日期: 2020-07-10

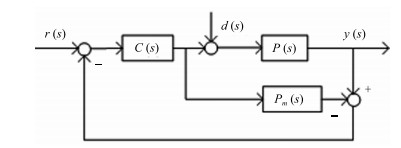
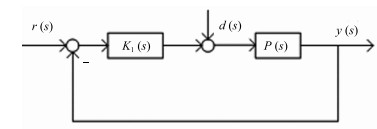
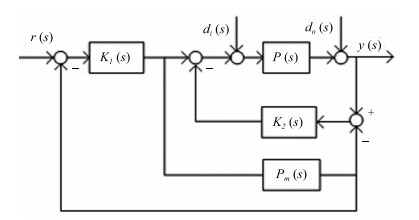
Two Degree of Freedom PID Control Based on Modified Smith Predictor Control Structure

YIN Cheng-Qiang^{1
, ,},
GAO Jie^1
,,
SUN Qun^1
,,
ZHAO Ying^1
,

1.
School of Mechanical and Automobile Engineering, Liaocheng University, Liaocheng 252059

Funds:

National Natural Science Foundation of China 61703192

Shandong Province Key Technologies Research and Development Program 2016GNC112014

Science and Technology Funds of Shandong Education Department J15LB09

More Information

Author Bio:
GAO Jie   Associate professor at the School of Mechanical and Automobile Engineering, Liaocheng University. Her research interest covers traffic control and transportation planning

SUN Qun   Professor at the School of Mechanical and Automobile Engineering, Liaocheng University. His research interest covers robotics, measurement, and control

ZHAO Ying    Professor at the School of Mechanical and Automobile Engineering, Liaocheng University. Her research interest covers machine vision and robotics

Corresponding author: YIN Cheng-Qiang Associate professor at the School of Mechanical and Automobile Engineering, Liaocheng University. His research interest covers process control and computer control. Corresponding author of this paper

摘要

摘要: 针对工业过程中的二阶不稳定时滞过程, 基于改进史密斯预估控制结构提出了一种简单的两自由度控制方案.设定值跟踪控制器和扰动抑制控制器采用同一设计程序, 并基于内模控制原理提出了控制器解析设计方案.设定值跟踪控制器和抗扰动控制器可分别通过单性能参数独立调节和优化, 每个控制器都具有PID形式, 给出了控制器调整参数的选择范围和扰动抑制闭环保证鲁棒稳定性的条件.仿真实例验证了提出方法对于近期其他方法的优越性.
- 改进史密斯预估控制 /
- 二自由度 /
- 二阶不稳定过程 /
- PID控制器
Abstract: A simple two degree of freedom control scheme is proposed for second-order unstable processes with time delay based on modified Smith predictor control structure. The set point tracking controller and the disturbance rejection controller are designed with the same procedure, and analytical design method on the basis of the internal model control (IMC) design principle is adopted for the two controllers. The controller for setpoint response and the controller for disturbance can be adjusted and optimized independently, and the two controllers are designed as PID form respectively. Suitable values for the adjustable parameters of two controllers and conditions holding the closed loop robust stability are recommended. Simulation examples demonstrate the superiority of the proposed method over recent other approaches.
- Modified Smith predictor control /
- two degree of freedom /
- second-order unstable process /
- PID controller
Recommended by Associate Editor SUN Jian
注释:

1) 本文责任编委孙健

HTML全文

图 1 改进Smith控制结构

Fig. 1 Modified Smith predictor structure

下载: 全尺寸图片幻灯片

图 2 内模控制结构

Fig. 2 IMC control structure

下载: 全尺寸图片幻灯片

图 3 单位反馈控制结构

Fig. 3 Feedback control structure

下载: 全尺寸图片幻灯片

图 4 例1标称系统阶跃响应

Fig. 4 Step responses for Example 1 (normal)

下载: 全尺寸图片幻灯片

图 5 例1标称系统控制响应

Fig. 5 Control signals for Example 1 (normal)

下载: 全尺寸图片幻灯片

图 6 例1扰动系统阶跃响应

Fig. 6 Step responses for Example 1 (perturbed)

下载: 全尺寸图片幻灯片

图 7 例1扰动系统控制响应

Fig. 7 Control signals for Example 1 (perturbed)

下载: 全尺寸图片幻灯片

图 8 例2标称系统阶跃响应

Fig. 8 Step responses for Example 2 (normal)

下载: 全尺寸图片幻灯片

图 9 例2扰动系统阶跃响应

Fig. 9 Step responses for Example 2 (perturbed)

下载: 全尺寸图片幻灯片

图 10 例3标称系统阶跃响应

Fig. 10 Step responses for Example 3 (normal)

下载: 全尺寸图片幻灯片

图 11 例3标称系统控制响应

Fig. 11 Control signals for Example 3 (normal)

下载: 全尺寸图片幻灯片

图 12 例3扰动系统阶跃响应

Fig. 12 Step responses for Example 3 (perturbed)

下载: 全尺寸图片幻灯片

图 13 例3扰动系统控制响应

Fig. 13 Control signals for Example 3 (perturbed)

下载: 全尺寸图片幻灯片

图 14 例1~3本文方法灵敏度函数幅值

Fig. 14 Magnitude plots of the proposed sensitivity function for Examples 1~3

下载: 全尺寸图片幻灯片

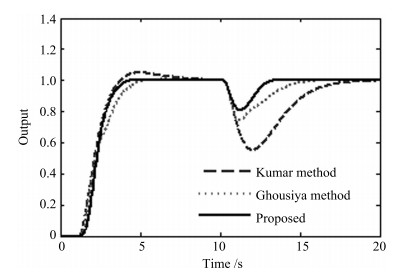
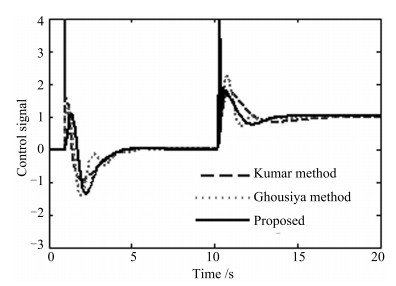
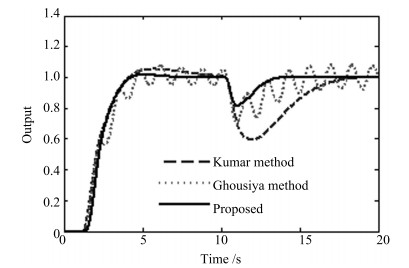
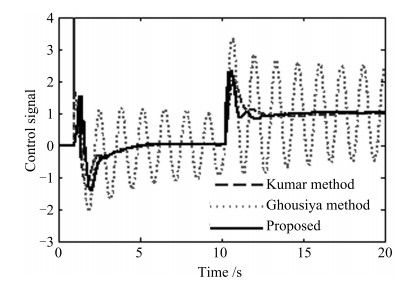
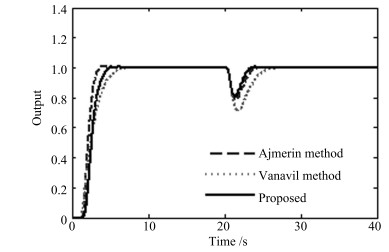
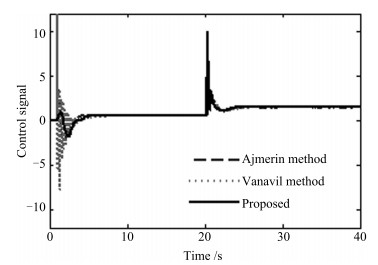
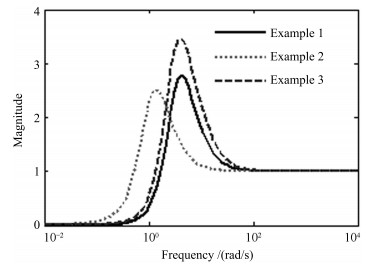
表 1 例1的性能指标

Table 1 Performance measures for Example 1

方法	${IAE}$	${ITAE}$	${OV}$	$PV$
标称响应
本文方法	1.40	2.58	1.00	1.0091
Kumar方法^[32]	1.41	3.13	1.05	1.1042
Ghousiya方法^[33]	1.52	3.14	1.01	1.0226
扰动响应
本文方法	1.75	7.75	1.02	1.4168
Kumar方法^[32]	3.01	31.09	1.05	1.9253
Ghousiya方法^[33]	2.90	27.29	1.08	6.2813

下载: 导出CSV

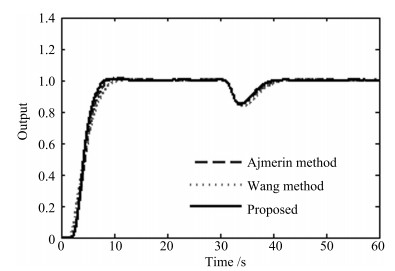
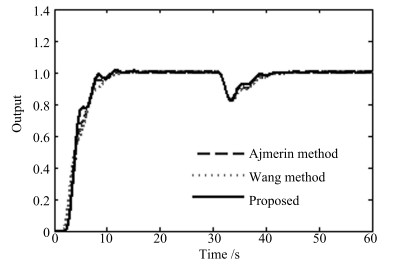
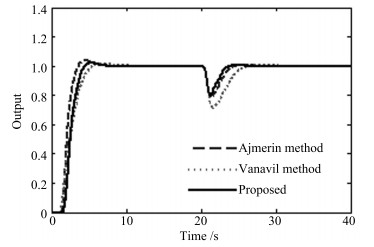
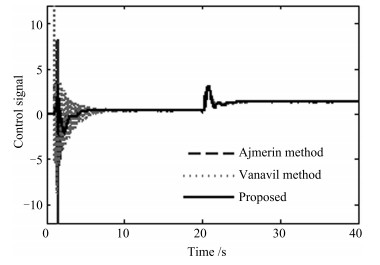
表 2 例2的性能指标

Table 2 Performance measures for Example 2

方法	${IAE}$	${ITAE}$	${OV}$	$PV$
标称响应
本文方法	3.57	10.94	1.00	1.0144
Ajmerin方法^[25]	3.71	12.15	1.00	1.0083
Wang方法^[28]	3.75	12.51	1.00	1.0052
扰动响应
本文方法	4.37	36.80	1.01	1.590
Ajmerin方法^[25]	4.67	41.29	1.01	1.535
Wang方法^[28]	4.70	44.70	1.00	1.381

下载: 导出CSV

表 3 例3的性能指标

Table 3 Performance measures for Example 3

方法	${IAE}$	${ITAE}$	${OV}$	$PV$
标称响应
本文方法	1.71	3.47	1.00	1.0121
Ajmerin方法^[25]	1.23	2.13	1.01	1.0230
Vanavil方法^[34]	1.75	3.88	1.00	1.0034
扰动响应
本文方法	2.04	11.82	1.02	1.4628
Ajmerin方法^[25]	1.70	13.36	1.04	1.5220
Vanavil方法^[34]	2.51	24.77	1.02	1.6185

下载: 导出CSV

参考文献(34)

[1]	Liu T, Gao F R. Enhanced IMC design of load disturbance rejection for integrating and unstable processes with slow dynamics. ISA Transactions, 2011, 50(2): 239-248 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8e1fec3de2fdfed6d47fd8bb1bfdf491
[2]	Vanavil B, Chaitanya K K, Rao A S. Improved PID controller design for unstable time delay processes based on direct synthesis method and maximum sensitivity. International Journal of Systems Science, 2015, 46(8): 1349-1366 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/00207721.2013.822124
[3]	Seer Q H, Nandong J. Stabilization and PID tuning algorithms for second-order unstable processes with time-delays. ISA Transactions, 2017, 67: 233-245 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3f176a0d140e7a7608a85c23a181ba10
[4]	Zhang G Q, Zhang X K, Zhang W D. Robust controller synthesis for high order unstable processes with time delay using mirror mapping technique. ISA Transactions, 2015, 59: 10-19 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=1ac171a7294c271e0940654622fe040b
[5]	Zhang G Q, Zhang X K, Guan W. Stability analysis and design of integrating unstable delay processes using the mirror-mapping technique. Journal of Process Control, 2014, 24(7): 1038-1045 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=32f9ba608ac7f42bb9c2e9bc7d4a9edc
[6]	肖强, 谢巍.针对时滞系统的一般化内模控制方法.自动化学报, 2011, 37(4): 464-470 doi: 10.3724/SP.J.1004.2011.00464 Xiao Qiang, Xie Wei. A GIMC architecture for timed- delay systems. Acta Automatica Sinica, 2011, 37(4): 464-470 doi: 10.3724/SP.J.1004.2011.00464
[7]	Wang Q G, Hang C C, Yang X P. Single-loop controller design via IMC principles. Automatica, 2001, 37(12): 2041- 2048 http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ029982756/
[8]	Skogestad S. Simple analytic rules for model reduction and PID controller tuning. Journal of Process Control, 2003, 13(4): 291-309 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_5e047a5c6dc4e7cd03e154e9ab666e46
[9]	Vanavil B, Anusha A V N L, Perumalsamy M, Seshagiri Rao A S. Enhanced IMC-PID controller design with lead lag filter for unstable and integrating processes with time delay. Chemical Engineering Communications, 2014, 201(11): 1468-1496 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/00986445.2013.818983
[10]	Begum K G, Rao A S, Radhakrishnan T K. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes. Chemical Engineering Research and Design, 2016, 109: 593-606 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d63e6a66a07fd73c35c40ed92ef1986f
[11]	汤赵建, 蒋北艳, 靳其兵.基于稳定裕度的新型IMC-PID整定方法.北京化工大学学报(自然科学版), 2017, 44(5): 105-110 http://d.old.wanfangdata.com.cn/Periodical/bjhgdxxb201705017 Tang Zhao-Jian, Jiang Bei-Yan, Jin Qi-Bing. A novel IMP-PID tuning method based on stability margin. Journal of Beijing University of Chemical Technology (Natural Science), 2017, 44(5): 105-110 http://d.old.wanfangdata.com.cn/Periodical/bjhgdxxb201705017
[12]	Das S, Pan I. On the mixed H₂/H_∞ loop-shaping tradeoffs in fractional-order control of the AVR system. IEEE Transactions on Industrial Informatics, 2014, 10(4): 1982-1991 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6813659
[13]	Zeng G Q, Chen J, Dai Y X, Li L M, Zheng C W, Chen M R. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing, 2015, 160: 173-184 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c2e4cf641143068fb90d95742a859d40
[14]	Zeng G Q, Chen J, Chen M R, Dai Y X, Li L M, Lu K D, et al. Design of multivariable PID controllers using real-coded population-based extremal optimization. Neurocomputing, 2015, 151(p3): 1343-1353 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b6ee227533eb1898f319add1076ab4df
[15]	Srivastava S, Pandit V S. A 2-Dof LQR based PID controller for integrating processes considering robustness/perf- ormance tradeoff. ISA Transactions, 2017, 71: 426-439 http://www.ncbi.nlm.nih.gov/pubmed/28941953
[16]	黄德先, 江永亨, 金以慧.炼油工业过程控制的研究现状、问题与展望.自动化学报, 2017, 43(6): 902-916 doi: 10.16383/j.aas.2017.c170157 Huang De-Xian, Jiang Yong-Heng, Jin Yi-Hui. Present research situation, major bottlenecks, and prospect of refinery industry process control. Acta Automatica Sinica, 2017, 43(6): 902-916 doi: 10.16383/j.aas.2017.c170157
[17]	许锋, 魏小丽, 任丽红, 罗雄麟.基于多变量广义预测控制的不稳定系统控制结构选择方法.自动化学报, 2013, 39(9): 1547-1551 doi: 10.3724/SP.J.1004.2013.01547 Xu Feng, Wei Xiao-Li, Ren Li-Hong, Luo Xiong-Lin. A control structure selection method based on multivariable generalized predictive control for unstable processes. Acta Automatica Sinica, 2013, 39(9): 1547-1551 doi: 10.3724/SP.J.1004.2013.01547
[18]	Zhang W D, Gu D Y, Wang W, Xu X M. Quantitative performance design of a modified Smith predictor for unstable processes with time delay. Industrial and Engineering Chemistry Research, 2004, 43(1): 56-62 doi: 10.1021/ie020732v
[19]	Rao A S, Chidambaram M. Analytical design of modified Smith predictor in a two-degrees-of-freedom control scheme for second order unstable processes with time delay. ISA Transactions, 2008, 47(4): 407-419 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6435258c4dd7966c63beeec35e8db89d
[20]	Mataušek M R, Ribic A I. Control of stable, integrating and unstable processes by the modified Smith predictor. Journal of Process Control, 2012, 22(1): 338-343 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b870f9103807aad1e7bf1b806c1d4427
[21]	Tan W, Marquez H J, Chen T W. IMC design for unstable processes with time delays. Journal of Process Control, 2003, 13(3): 203-213 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=66f4025470065e24910842db889a173f
[22]	刘涛, 张卫东, 顾诞英.化工不稳定时滞过程鲁棒控制的解析设计.控制与决策, 2005, 20(5): 575-578 http://d.old.wanfangdata.com.cn/Periodical/kzyjc200505021 Liu Tao, Zhang Wei-Dong, Gu Dan-Ying. Analytical design of robust control for unstable chemical and industrial processes with time delay. Control and Decision, 2005, 20(5): 575-578 http://d.old.wanfangdata.com.cn/Periodical/kzyjc200505021
[23]	李敏, 王琪, 靳其兵.不稳定时滞对象的最优鲁棒二自由度控制器解析设计.信息与控制, 2016, 45(3): 313-319 http://d.old.wanfangdata.com.cn/Periodical/xxykz201603009 Li Min, Wang Qi, Jin Qi-Bing. Analytical design of optimal robust two-degree-of-freedom controller for unstable processes with time delays. Information and Control, 2016, 45(3): 313-319 http://d.old.wanfangdata.com.cn/Periodical/xxykz201603009
[24]	张井岗, 秦娜娜.串级不稳定时滞过程的内模控制器设计.电子科技大学学报, 2017, 46(1): 38-45 http://d.old.wanfangdata.com.cn/Periodical/dzkjdxxb201701007 Zhang Jing-Gang, Qin Na-Na. Design method of IMC controllers for unstable cascade processes with time delay. Journal of University of Electronic Science and Technology of China, 2017, 46(1): 38-45 http://d.old.wanfangdata.com.cn/Periodical/dzkjdxxb201701007
[25]	Ajmerin M, Ali A. Two degree of freedom control scheme for unstable processes with small time delay. ISA Transactions, 2015, 56: 308-326 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9931740737a8f15b4459b0b2ae4575dc
[26]	Padhy P K, Majhi S. Relay based PI-PD design for stable and unstable FOPDT processes. Computers and Chemical Engineering, 2006, 30(5): 790-796 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bda09cc6bb838ac1f3f64fb41ed23eb2
[27]	Vijayan V, Panda R C. Design of PID controllers in double feedback loops for SISO systems with set-point filters. ISA Transactions, 2012, 51(4): 514-521 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=444f11695ce4d7cd29885d7f30eb8784
[28]	Wang Q, Lu C H, Pan W. IMC PID controller tuning for stable and unstable processes with time delay. Chemical Engineering Research and Design, 2016, 105: 120-129 http://d.old.wanfangdata.com.cn/Periodical/zngydxxb-e202001009
[29]	Shamsuzzoha M, Lee M Y. Analytical design of enhanced PID filter controller for integrating and first order unstable processes with time delay. Chemical Engineering Science, 2008, 63 (10): 2717-273 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=222edd6e81fe5983e2d98f50d5d7756c
[30]	Wang Q G, Lee T H, He J B. Internal stability of interconnected systems. IEEE Transactions on Automatic Control, 1999, 44(3): 593-596 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e990bea0df126be8bf195b52d94ed9a5
[31]	Morari M, Zafiriou E. Robust Process Control. Englewood Cliffs: Prentice Hall, 1989.
[32]	Kumar D B, Padma S R. Tuning of IMC based PID controllers for integrating systems with time delay. ISA Transactions, 2016, 63: 242-255 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a77656da8528daf16c67ce90d58bc992
[33]	Ghousiya B K, Rao A S, Radhakrishnan T K. Enhanced IMC based PID controller design for non-minimum phase (NMP) integrating processes with time delays. ISA Transactions, 2017, 68: 223-234 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a0b2f8c7401d9fdd9546386d956a774b
[34]	Vanavil B, Rao A S. Improved performance with PID filter controllers for unstable processes involving time delays. In: Proceedings of the 2011 International Conference on Process Automation, Control, and Computing. New York, USA: IEEE, 2011. 1-6

施引文献

资源附件(0)

访问统计

图(14) / 表(3)

计量

文章访问数: 1366
HTML全文浏览量: 242
PDF下载量: 279
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于改进Smith预估控制结构的二自由度PID控制

doi: 10.16383/j.aas.2018.c170596

通讯作者:
尹成强聊城大学机械与汽车工程学院副教授.主要研究方向为过程控制与计算机控制.本文通信作者.E-mail: shtjycq@163.com

计量

Two Degree of Freedom PID Control Based on Modified Smith Predictor Control Structure

Corresponding author: YIN Cheng-Qiang Associate professor at the School of Mechanical and Automobile Engineering, Liaocheng University. His research interest covers process control and computer control. Corresponding author of this paper

计量

目录

留言板

基于改进Smith预估控制结构的二自由度PID控制

doi: 10.16383/j.aas.2018.c170596

通讯作者: 尹成强 聊城大学机械与汽车工程学院副教授.主要研究方向为过程控制与计算机控制.本文通信作者.E-mail: shtjycq@163.com

计量

出版历程

Two Degree of Freedom PID Control Based on Modified Smith Predictor Control Structure

Corresponding author: YIN Cheng-Qiang Associate professor at the School of Mechanical and Automobile Engineering, Liaocheng University. His research interest covers process control and computer control. Corresponding author of this paper

计量

出版历程

目录

通讯作者:
尹成强聊城大学机械与汽车工程学院副教授.主要研究方向为过程控制与计算机控制.本文通信作者.E-mail: shtjycq@163.com