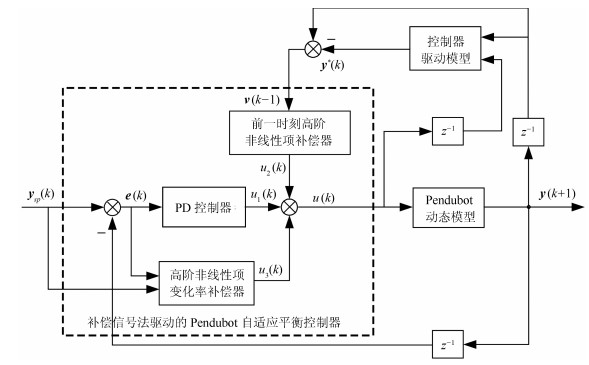
-
摘要: Pendubot是以电机转矩为输入，主动臂角度和欠驱动臂角度为输出的强非线性、多变量、欠驱动机械系统，受到具有时变不确定性的摩擦影响，且模型参数随摆臂质量与长度的改变而变化.本文将上述被控对象采用确定线性模型与未知高阶非线性项来描述，设计消除前一时刻高阶非线性项及其变化率对系统输出影响的补偿器，叠加于基于确定线性模型设计的PD控制器，提出了补偿信号法驱动的自适应平衡控制方法，并对所提方法进行了稳定性和收敛性分析.仿真和物理对比实验表明，当Pendubot系统模型参数改变时，所提控制算法可以有效地消除摩擦的影响，将两摆臂输出角度稳定在目标位置.Abstract: The Pendubot system is a strong nonlinear multivariable underactuated mechanical system with the motor torque as the input, angles of the actuated link and the underactuated link as outputs. The model parameters, such as the length of the link, the center of mass, change with the system mechanical structure. Moreover, the system is influenced by the friction, which is uncertain, nonlinear and time varying. In this paper, a novel compensation signal driven adaptive controller is developed by representing the controlled object as the combination of a determinate low-order linear model and unknown high-order nonlinear terms. In the proposed controller design, two compensation signals are constructed and added onto the control signal obtained from the linear deterministic model based PD control design. Such two compensation signals aim at eliminating the effects of the previous sample high-order nonlinearity and its changing rate, respectively. The performance analysis of the algorithm is given, and simulations and physical experiments are carried out, where it has been shown that the two output angles of the Pendubot can be stabilized at their targeted positions when the system is subjected to unknown variations of its parameters.1) 本文责任编委 梅生伟
-
图 2 补偿信号法驱动的Pendubot自适应平衡控制结构图
Fig. 2 Structure diagram of Pendubot adaptive balance control using the compensation signal based approach
表 1 本文控制方法与文献[15]控制方法的性能指标
Table 1 Performance indexes of the control method in [15] and the proposed control method
下载: 导出CSV
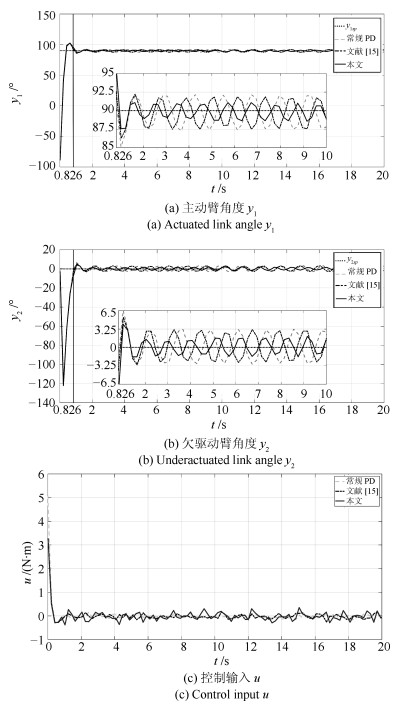
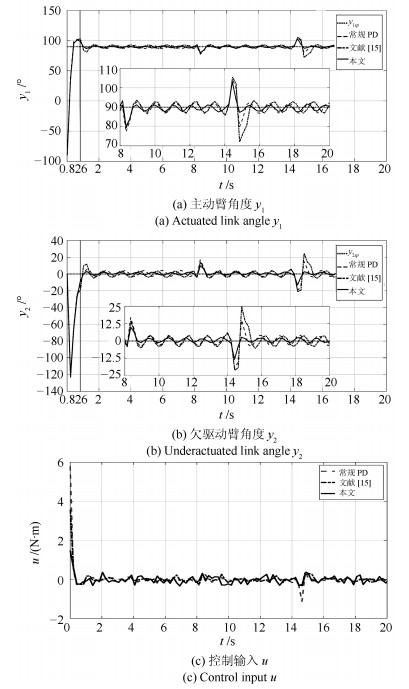
表 2 常规PD、文献[15]及本文控制方法的性能指标
Table 2 Performance indexes of the conventional PD method, the method in [15] and the proposed method
绝对误差累积和 误差均方差 常规PD 17 950.004 1.780 文献[15] 33 762.650 2.656 本文 11 233.987 1.762
下载: 导出CSV
-
[1] Spong W M. Underactuated mechanical systems. In:Control Problems in Robotics and Automation. Lecture Notes in Control and Information Sciences, Vol. 230. Berlin:Springer, 1998. 135-150 [2] Batista P, Silvestre C, Oliveira P. A sensor-based controller for homing of underactuated AUVs. IEEE Transactions on Robotics, 2009, 25(3):701-716 doi: 10.1109/TRO.2009.2014496 [3] Bechlioulis C P, Karras G C, Heshmati-Alamdari S, Kyriakopoulos K J. Trajectory tracking with prescribed performance for underactuated underwater vehicles under model uncertainties and external disturbances. IEEE Transactions on Control Systems Technology, 2017, 25(2):429-440 doi: 10.1109/TCST.2016.2555247 [4] Chwa D. Tracking control of differential-drive wheeled mobile robots using a backstepping-like feedback linearization. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2010, 40(6):1285-1295 doi: 10.1109/TSMCA.2010.2052605 [5] Sun N, Fang Y C, Chen H. A new antiswing control method for underactuated cranes with unmodeled uncertainties:theoretical design and hardware experiments. IEEE Transactions on Industrial Electronics, 2015, 62(1):453-465 doi: 10.1109/TIE.2014.2327569 [6] 王永富, 王殿辉, 柴天佑.基于状态估计的摩擦模糊建模与鲁棒自适应控制.自动化学报, 2011, 37(2):245-252 http://www.aas.net.cn/CN/abstract/abstract17430.shtmlWang Yong-Fu, Wang Dian-Hui, Chai Tian-You. State estimate-based friction fuzzy modeling and robust adaptive control. Acta Automatica Sinica, 2011, 37(2):245-252 http://www.aas.net.cn/CN/abstract/abstract17430.shtml [7] Spong M W, Block D J. The Pendubot:a mechatronic system for control research and education. In:Proceedings of the 34th IEEE Conference on Decision and Control. New Orleans, LA, USA:IEEE, 1995. 555-556 [8] Erdem E B, Alleyne A G. Experimental real-time SDRE control of an underactuated robot. In:Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, FL, USA:IEEE, 2001. 2986-2991 [9] Zhang M J, Tarn T J. Hybrid control of the Pendubot. IEEE/ASME Transactions on Mechatronics, 2002, 7(1):79-86 doi: 10.1109/3516.990890 [10] Xin X, Liu Y N. Reduced-order stable controllers for two-link underactuated planar robots. Automatica, 2013, 49(7):2176-2183 doi: 10.1016/j.automatica.2013.03.027 [11] Sanchez E N, Flores V. Real-time fuzzy PI + PD control for an underactuated robot. In:Proceedings of the 2002 IEEE International Symposium on Intelligent Control. Vancouver, BC, Canada:IEEE, 2002. 137-141 [12] Wang W, Yi J Q, Zhao D B, Liu X J. Adaptive sliding mode controller for an underactuated manipulator. In:Proceedings of the 2004 International Conference on Machine Learning and Cybernetics. Shanghai, China:IEEE, 2004. 882-887 [13] 侯俊, 王良勇, 柴天佑, 方正.基于T-S模糊的欠驱动机械臂的平衡控制.控制工程, 2012, 19(1):5-8 http://d.old.wanfangdata.com.cn/Periodical/jczdh201201002Hou Jun, Wang Liang-Yong, Chai Tian-You, Fang Zheng. Balance control of underactuated manipulator using T-S fuzzy scheme. Control Engineering of China, 2012, 19(1):5-8 http://d.old.wanfangdata.com.cn/Periodical/jczdh201201002 [14] 王永富, 王殿辉, 柴天佑.基于数据挖掘与系统理论建立摩擦模糊模型与控制补偿.自动化学报, 2010, 36(3):412-420 http://www.aas.net.cn/CN/abstract/abstract13682.shtmlWang Yong-Fu, Wang Dian-Hui, Chai Tian-You. Data mining and systems theory based fuzzy modeling and control compensation for friction. Acta Automatica Sinica, 2010, 36(3):412-420 http://www.aas.net.cn/CN/abstract/abstract13682.shtml [15] Eom M, Chwa D. Robust swing-up and balancing control using a nonlinear disturbance observer for the Pendubot system with dynamic friction. IEEE Transactions on Robotics, 2015, 31(2):331-343 doi: 10.1109/TRO.2015.2402512 [16] Sun N, Fang Y C, Chen H, Lu B, Fu Y M. Slew/Translation positioning and swing suppression for 4-DOF tower cranes with parametric uncertainties:design and hardware experimentation. IEEE Transactions on Industrial Electronics, 2016, 63(10):6407-6418 doi: 10.1109/TIE.2016.2587249 [17] 张亚军, 柴天佑, 杨杰.一类非线性离散时间动态系统的交替辨识算法及应用.自动化学报, 2017, 43(1):101-113 http://www.aas.net.cn/CN/abstract/abstract18992.shtmlZhang Ya-Jun, Chai Tian-You, Yang Jie. Alternating identification algorithm and its application to a class of nonlinear discrete-time dynamical systems. Acta Automatica Sinica, 2017, 43(1):101-113 http://www.aas.net.cn/CN/abstract/abstract18992.shtml [18] Chai T Y, Zhang Y J, Wang H, Su C Y, Sun J. Data-based virtual unmodeled dynamics driven multivariable nonlinear adaptive switching control. IEEE Transactions on Neural Networks, 2011, 22(12):2154-2172 doi: 10.1109/TNN.2011.2167685 [19] 柴天佑, 岳恒.自适应控制.北京:清华大学出版社, 2016.Chai Tian-You, Yue Heng. Adaptive Control. Beijing:Tsinghua University Press, 2016. [20] Goodwin G C, Ramadge P J, Caines P E. Discrete time multivariable adaptive control. IEEE Transactions on Automatic Control, 1980, 25(3):449-456 doi: 10.1109/TAC.1980.1102363 [21] Aguilar-Avelar C, Moreno-Valenzuela J. New feedback linearization-based control for arm trajectory tracking of the Furuta pendulum. IEEE/ASME Transactions on Mechatronics, 2016, 21(2):638-648 doi: 10.1109/TMECH.2015.2485942 -
图(7) / 表(4)
计量
- 文章访问数: 2048
- HTML全文浏览量: 337
- PDF下载量: 390
- 被引次数: 0
