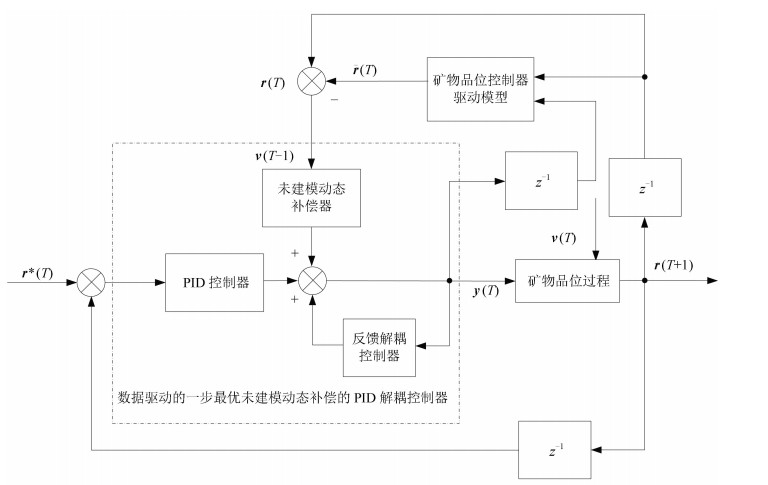
-
摘要: 浮选过程是利用矿物本身的亲水或疏气性质或经药剂处理得到的亲水或疏气性质进行矿物分离的物理过程.本文通过建立以矿浆液位和矿浆流量为输入，以浮选过程的精矿品位与尾矿品位为输出的多变量、强耦合、非线性、时变的运行过程模型，利用未建模动态前一拍可测的特点，提出了包括矿物品位运行过程控制器驱动模型、PID控制器、反馈解耦控制器、未建模动态补偿器的数据驱动的一步最优未建模动态补偿PID解耦控制方法，实现了消除稳态误差、静态解耦与未建模动态的补偿，通过浮选过程运行反馈控制仿真实验验证了本文所提方法的有效性.Abstract: The flotation process is a mineral separating physical process by taking advantage of the hydrophilic or hydrophobic properties of the mineral or the hydrophilic or hydrophobic properties obtained by treatment. In this paper, firstly, a multivariable, strong coupling, nonlinear and time-varying operational process model is established with the input and output of the pulp level and feed flow as its inputs and the concentrate grade and tailing grade as its outputs. Secondly, by taking the advantage that the unmodeled dynamics at last sampling point can be measured, a scheme of one-step optimal unmodeled dynamic compensation PID decoupling control is proposed including the ore grade operational process controller driven model, PID controller, feedback decoupling controller and unmodeled dynamic compensator, to guarantee zero steady-state error, static decoupling, and unmodeled dynamics compensation. Finally, a simulation experiment on the operational feedback control in an industrial flotation process is conducted to demonstrate the effectiveness of the proposed method.
-
Key words:
- Data-driven /
- flotation processes /
- operational control /
- decoupling
1) 本文责任编委 侯忠生 -
图 2 数据驱动一步最优未建模动态补偿PID解耦控制结构图
Fig. 2 Structure diagram of data driven one-step optimal unmodeled dynamic compensation PID decoupling control
图 3 线性模型下PID解耦控制的矿物品位跟踪曲线
Fig. 3 Ore grade tracking curve with PID decoupling control under linear model
图 4 线性模型下PID解耦控制的控制输入
Fig. 4 Control input curve with PID decoupling control under linear model
图 5 线性模型下模型预测控制控制的矿物品位跟踪曲线
Fig. 5 Ore grade tracking curve with MPC under linear model
图 8 非线性模型下数据驱动一步最优未建模动态补偿的PID解耦控制的矿物品位跟踪曲线
Fig. 8 Ore grade tracking curve with data driven one step optimal unmolded dynamic compensation PID decoupling control under nonlinear model
图 9 非线性模型下数据驱动一步最优未建模动态补偿的PID解耦控制的控制输入
Fig. 9 Control input curve with data driven one step optimal unmolded dynamic compensation PID decoupling control under nonlinear model
图 11 非线性模型下模型预测控制的矿物品位跟踪曲线
Fig. 11 Ore grade tracking curve with MPC under nonlinear model
表 1 浮选过程符号表
Table 1 Flotation process symbol table
符号 物理含义 $k_p^1$ 黄铜矿浮选率 $k_e^1$ 黄铜矿排放率 $g_{a}$ 原矿浆黄铜矿品位 $X_a^2$ 脉石矿浆浓度 $H$ 浮选槽高度 $L_{cu}$ 黄铜矿矿物品位 $g_{cp}^1$ 黄铜矿浆的 黄铜矿品位 $k_p^2$ 脉石浮选率 $k_e^2$ 脉石排放率 $X_a^1$ 黄铜矿浆浓度 $A$ 浮选槽底面积 ${q_T}$ 尾矿流量 ${q_c}$ 精矿流量 $g_{cp}^2$ 脉石矿浆的 黄铜矿品位 
下载: 导出CSV
表 2 对比实验评价指标
Table 2 Performance index of comparison experiment
IAE MSE 本文$r_1$ 0.2078 $3.3073\times10^{-5}$ 本文$r_2$ 0.1803 $2.396\times10^{-5}$ MPC $r_1$ 18.1797 0.0601 MPC $r_2$ 37.4461 0.2563
下载: 导出CSV
-
[1] 柴天佑.复杂工业过程运行优化与反馈控制.自动化学报, 2013, 39(11):1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtmlChai Tian-You. Operational optimization and feedback control for complex industrial processes. Acta Automatica Sinica, 2013, 39(11):1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtml [2] 范家璐, 姜艺, 柴天佑.无线网络环境下工业过程运行反馈控制方法.自动化学报, 2016, 42(8):1166-1174 http://www.aas.net.cn/CN/abstract/abstract18906.shtmlFan Jia-Lu, Jiang Yi, Chai Tian-You. Operational feedback control of industrial processes in a wireless network environment. Acta Automatica Sinica, 2016, 42(8):1166-1174 http://www.aas.net.cn/CN/abstract/abstract18906.shtml [3] Chai T Y, Qin S J, Wang H. Optimal operational control for complex industrial processes. Annual Reviews in Control, 2014, 38(1):81-92 doi: 10.1016/j.arcontrol.2014.03.005 [4] 杨亚茹, 李少远.切换非线性系统全局优化运行的经济预测控制.自动化学报, 2017, 43(6):1017-1027 http://www.aas.net.cn/CN/abstract/abstract19077.shtmlYang Ya-Ru, Li Shao-Yuan. Economic model predictive control for global optimal operation of nonlinear switching systems. Acta Automatica Sinica, 2017, 43(6):1017-1027 http://www.aas.net.cn/CN/abstract/abstract19077.shtml [5] 张翔宇, 李继庚, 周平, 张占波, 刘焕彬, 王宏.制浆氯漂过程运行优化控制系统.控制工程, 2014, 21(2):303-308 doi: 10.3969/j.issn.1671-7848.2014.02.032Zhang Xiang-Yu, Li Ji-Geng, Zhou Ping, Zhang Zhan-Bo, Liu Huan-Bin, Wang Hong. Operational optimization control system for pulp chlorination process. Control Engineering of China, 2014, 21(2):303-308 doi: 10.3969/j.issn.1671-7848.2014.02.032 [6] 刘晓青, 程全, 李晋, 周小东.浮选生产过程综合自动化系统.控制工程, 2016, 23(11):1702-1706 http://d.old.wanfangdata.com.cn/Periodical/jczdh201611011Liu Xiao-Qing, Cheng Quan, Li Jin, Zhou Xiao-Dong. Integrated automation system for flotation processes. Control Engineering of China, 2016, 23(11):1702-1706 http://d.old.wanfangdata.com.cn/Periodical/jczdh201611011 [7] Wang R H, Qiu M J, Zhao K L, Qian Y. Optimal RTO timer for best transmission efficiency of DTN protocol in deep-space vehicle communications. IEEE Transactions on Vehicular Technology, 2017, 66(3):2536-2550 doi: 10.1109/TVT.2016.2572079 [8] 潘红光, 高海南, 孙耀, 张英, 丁宝苍.基于多优先级稳态优化的双层结构预测控制算法及软件实现.自动化学报, 2014, 40(3):405-414 http://www.aas.net.cn/CN/abstract/abstract18305.shtmlPan Hong-Guang, Gao Hai-Nan, Sun Yao, Zhang Ying, Ding Bao-Cang. The algorithm and software implementation for double-layered model predictive control based on multi-priority rank steady-state optimization. Acta Automatica Sinica, 2014, 40(3):405-414 http://www.aas.net.cn/CN/abstract/abstract18305.shtml [9] Ding J L, Modares H, Chai T, Lewis F L. Data-based multiobjective plant-wide performance optimization of industrial processes under dynamic environments. IEEE Transactions on Industrial Informatics, 2016, 12(2):454-465 doi: 10.1109/TII.2016.2516973 [10] Wang T, Gao H J, Qiu J B. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(2):416-425 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4d9bb8f6ad6ba73ffa67e57947d5211f [11] Yang X P, Chen Y R. Intelligent control and optimization of the coal slime flotation. Advanced Materials Research, 2012, 524-527:1007-1010 doi: 10.4028/www.scientific.net/AMR.524-527 [12] Li H B, Chai T Y, Zhang L Y. Hybrid intelligent optimal control for flotation processes. In: Proceedings of the 2012 American Control Conference (ACC). Montreal, QC, Canada: IEEE, 2012. 4891-4896 [13] Jiang Y, Fan J L, Chai T Y, Li J N, Lewis F L. Data-driven flotation industrial process operational optimal control based on reinforcement learning. IEEE Transactions on Industrial Informatics, 2018, 14(5):1974-1989 doi: 10.1109/TII.2017.2761852 [14] Jiang Y, Fan J L, Chai T Y, Lewis F L. Dual-rate operational optimal control for flotation industrial process with unknown operational model. IEEE Transactions on Industrial Electronics, 2019, 66(6):4587-4599 doi: 10.1109/TIE.2018.2856198 [15] Rojas D, Cipriano A. Model based predictive control of a rougher flotation circuit considering grade estimation in intermediate cells. Dyna, 2011, 78(166):29-37 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_a93b7dd58593186e6d3c37cdada94186 [16] Jiang Y, Fan J L, Chai T Y, Chen T W. Setpoint dynamic compensation via output feedback control with network induced time delays. In: Proceedings of the 2015 American Control Conference (ACC). Chicago, IL, USA: IEEE, 2015: 5384-5389 [17] Wang T, Gao H J, Qiu J B. A combined fault-tolerant and predictive control for network-based industrial processes. IEEE Transactions on Industrial Electronics, 2016, 63(4):2529-2536 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b49c2d011b2aa58addfb405f23a867fc [18] Fan J L, Jiang Y, Chai T Y. MPC-based setpoint compensation with unreliable wireless communications and constrained operational conditions. Neurocomputing, 2017, 270:110-121 doi: 10.1016/j.neucom.2016.10.098 [19] Jury E I. Inners and Stability of Dynamic Systems. Malabar, Florida, India:Krieger Pub Co, 1982. [20] 柴天佑.多变量自适应解耦控制及应用.北京:科学出版社, 2001.Chai Tian-You. Multivariable Adaptive Decoupling Control and Its Application. Beijing:Science Press, 2001. [21] Chai T Y, Zhai L F, Yue H. Multiple models and neural networks based decoupling control of ball mill coal-pulverizing systems. Journal of Process Control, 2011, 21(3):351-366 doi: 10.1016/j.jprocont.2010.11.007 [22] 贾瑶, 岳恒, 柴天佑.高压酸浸过程多工况切换控制方法.控制理论与应用, 2014, 31(10):1318-1326 doi: 10.7641/CTA.2014.30886Jia Yao, Yue Heng, Chai Tian-You. Multi-operation condition switching control for high pressure acid leaching process. Control Theory and Applications, 2014, 31(10):1318-1326 doi: 10.7641/CTA.2014.30886 [23] Hägglund T. A control-loop performance monitor. Control Engineering Practice, 1995, 3(11):1543-1551 doi: 10.1016/0967-0661(95)00164-P [24] 贾瑶, 柴天佑.汽水板式换热过程区间串级智能控制方法.自动化学报, 2016, 42(1):37-46 http://www.aas.net.cn/CN/abstract/abstract18794.shtmlJia Yao, Chai Tian-You. Interval cascade intelligent control in vaper-water plate-type heat exchange process. Acta Automatica Sinica, 2016, 42(1):37-46 http://www.aas.net.cn/CN/abstract/abstract18794.shtml [25] Jia Y, Chai T Y. A data-driven dual-rate control method for a heat exchanging process. IEEE Transactions on Industrial Electronics, 2017, 64(5):4158-4168 doi: 10.1109/TIE.2016.2608878 [26] 王兰豪, 贾瑶, 柴天佑.再磨过程的泵池液位和给矿压力双速率区间控制.自动化学报, 2017, 43(6):993-1006 http://www.aas.net.cn/CN/abstract/abstract19075.shtmlWang Lan-Hao, Jia Yao, Chai Tian-You. Dual-rate interval control of pump pool level and feeding pressure during regrinding. Acta Automatica Sinica, 2017, 43(6):993-1006 http://www.aas.net.cn/CN/abstract/abstract19075.shtml -
计量
- 文章访问数: 2865
- HTML全文浏览量: 405
- PDF下载量: 703
- 被引次数: 0
