-
摘要: 针对机器人图像压缩感知(Compressed sensing, CS)过程中稀疏字典训练时间过长的问题, 本文提出了一种更加高效的字典学习方法.通过对MOD、K-SVD、SGK等字典学习算法研究, 从参与更新的字典原子列数入手, 将残差项变形为多列原子同时更新, 进而利用最小二乘法连续地更新字典中的多个原子.本文算法是对SGK算法字典学习效率的进一步提高, 减少了单次迭代的计算量, 加快了字典学习速度.实验表明, 本文算法与K-SVD和SGK算法相比, 在字典稀疏性和重构图像质量变化很小的情况下, 字典训练时间得到较明显缩短.Abstract: Aiming at the problem that the time of dictionary training is too long in the process of robot image compressed sensing (CS), a more efficient dictionary learning algorithm is proposed in this paper. Through the research of MOD, K-SVD, SGK and other dictionary learning algorithms, we start with the number of dictionary atoms involved in the update, and change the residuals into multiple atoms updating at the same time. Then, we can update the multiple atoms of the dictionary sequentially by using the least square method. The algorithm is to further improve the efficiency of the SGK algorithm, and to reduce the computation of single iteration. The experiment results show that the improved algorithm can effectively shorten the dictionary training time under the premise of ensuring sparsity of the dictionary and the quality of the reconstructed image.
-
Key words:
- Compressed sensing (CS) /
- sparse representation /
- dictionary learning /
- the least squares method
1) 本文责任编委 黎铭 -
表 1 不同字典原子选取方式效果对比
Table 1 Comparison of the effects for different selections of dictionary atoms
选取待更新字典原子的方式 顺次选取连续的2列 随机选取连续的2列 随机选取离散的2列 字典学习时间(s) 3.994 5.268 6.788 峰值信噪比PSNR (dB) 32.092 31.968 31.866 平均结构相似度MSSIM 0.3183 0.3152 0.3114 表 2 同时更新不同字典列数效果对比
Table 2 Effect comparison of updating different numbers of dictionary columns at the same time
同时更新原子列数 2 4 8 16 32 64 字典学习时间(s) 4.117 4.194 3.630 3.744 4.032 4.093 峰值信噪比PSNR (dB) 32.092 32.065 32.081 32.145 32.058 32.045 平均结构相似度MSSIM 0.3183 0.3176 0.3177 0.3173 0.3164 0.3181 表 3 不同算法的重构效果
Table 3 Reconstruction effect with different algorithms
算法 DCT字典 K-SVD字典 SGK字典 本文算法字典 字典学习时间(s) -- 20.079 4.254 3.605 峰值信噪比PSNR (dB) 30.915 31.950 31.935 31.947 平均结构相似度MSSIM 0.3022 0.3149 0.3137 0.3144 表 4 不同迭代次数重构图像质量
Table 4 The quality of the reconstructed image with different numbers of iteration
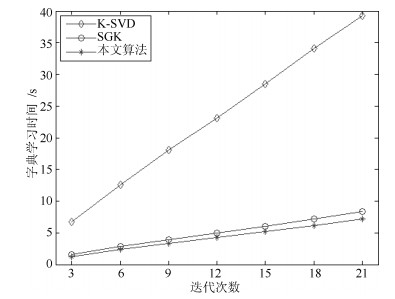
迭代次数 K-SVD字典 SGK字典 本文算法字典 PSNR (dB) MSSIM PSNR (dB) MSSIM PSNR (dB) MSSIM 3 31.4559 0.30762 31.4459 0.30779 31.4603 0.30825 6 31.9951 0.31384 31.9291 0.31171 31.9265 0.31207 9 31.9704 0.31386 31.9490 0.31287 31.9194 0.31313 12 32.2901 0.31418 32.2661 0.31423 32.2416 0.31279 15 32.3571 0.31986 32.3297 0.31898 32.2724 0.31921 18 32.4407 0.32208 32.3781 0.32182 32.3485 0.32141 21 32.4489 0.32209 32.4040 0.32206 32.3971 0.32172 表 5 不同噪声水平下重构图像质量
Table 5 The quality of the reconstructed image with different noise levels
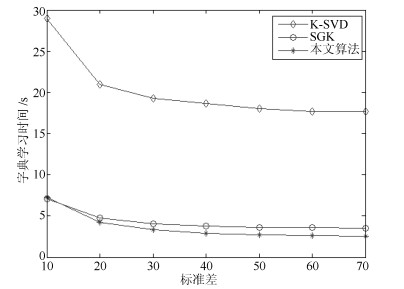
标准差 K-SVD字典 SGK字典 本文算法字典 PSNR (dB) MSSIM PSNR (dB) MSSIM PSNR (dB) MSSIM 10 35.9741 0.45381 35.9440 0.45390 35.9620 0.45430 20 33.2254 0.34207 33.1664 0.34219 33.2006 0.34282 30 31.3615 0.30139 31.2992 0.29996 31.3157 0.29984 40 29.4226 0.26534 29.3889 0.26387 29.4074 0.26427 50 28.0932 0.23598 28.0699 0.23470 28.0908 0.23485 60 26.8134 0.20862 26.8110 0.20815 26.8230 0.20744 70 25.6137 0.18573 25.6164 0.18493 25.6238 0.18591 表 6 不同图像信号的重构效果
Table 6 Reconstruction effect of different image signals
图像 算法 时间(s) MSSIM PSNR (dB) lena K-SVD 18.343162 0.27010 25.8505 SGK 3.891636 0.26863 25.8154 本文算法 3.102337 0.26916 25.8230 peppers K-SVD 19.244135 0.35640 26.1407 SGK 4.141303 0.35574 26.1445 本文算法 3.092842 0.35545 26.1353 barbara K-SVD 19.438234 0.35642 25.2067 SGK 4.114145 0.35763 25.1997 本文算法 3.197942 0.35774 25.2009 表 7 不同场景自然图像信号的重构效果
Table 7 Reconstruction effect of image signals in different natural scenes
图像 时间(s) MSSIM PSNR (dB) K-SVD SGK 本文算法 K-SVD SGK 本文算法 K-SVD SGK 本文算法 (a)明 20.196063 4.470679 3.958860 0.35006 0.35036 0.35019 26.3382 26.3285 26.3339 (a)暗 19.138866 4.303163 3.779787 0.25134 0.25155 0.25157 27.0640 27.0637 27.0611 (b)视角1 19.294378 4.068634 3.263159 0.29148 0.29095 0.29066 25.9845 25.9772 29.9781 (b)视角2 21.498433 4.167165 3.233882 0.30110 0.30121 0.30176 28.2839 28.2803 28.2971 (c)清晰 20.856516 4.534554 4.031721 0.35926 0.35839 0.35854 26.0795 26.0734 26.0601 (c)模糊 18.319955 3.874162 2.932584 0.41004 0.41013 0.40993 29.4348 29.4386 29.4385 -
[1] Candes E J. Compressive sampling. In: Proceedings of International Congress of Mathematicians. Madrid, Spain: European Mathematical Society Publishing House, 2006. 1433-1452 [2] 任越美, 张艳宁, 李映.压缩感知及其图像处理应用研究进展与展望.自动化学报, 2014, 40(8): 1563-1575 doi: 10.3724/SP.J.1004.2014.01563Ren Yue-Mei, Zhang Yan-Ning, Li Ying. Advances and perspective on compressed sensing and application on image processing. Acta Automatica Sinica, 2014, 40(8): 1563-1575 doi: 10.3724/SP.J.1004.2014.01563 [3] 占新.基于字典学习与稀疏模型的SAR图像压缩技术研究[Ph. D. dissertation].中国科学技术大学, 2015Zhan Xin. Research on Dictionary Learning-based SAR Image Compression Techbique[Ph. D. dissertation], University of Science and Technology of China, China, 2015 [4] Olshausen B A, Field D J. Emergency of simple-cell receptive fleld properties by learning a sparse code for natural images. Nature, 1996, 381(6583): 607-609 doi: 10.1038/381607a0 [5] Engan K, Aase S O, Husoy J H. Method of optimal directions for frame design. In: Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing. Phoenix, AZ, USA: IEEE, 1999. 2443-2446 [6] Aharon M, Elad M, Bruckstein A M. The K-SVD: an algorithm for designing of overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322 doi: 10.1109/TSP.2006.881199 [7] 王强, 张培林, 王怀光, 吴定海, 张云强.基于稀疏分解的振动信号数据压缩算法.仪器仪表学报, 2016, 37(11): 2497-2505 doi: 10.3969/j.issn.0254-3087.2016.11.012Wang Qiang, Zhang Pei-Lin, Wang Huai-Guang, Wu Ding-Hai, Zhang Yun-Qiang. Data compression algorithm of vibration signal based on sparse decomposition. Chinese Journal of Scientific Instrument, 2016, 37(11): 2497-2505 doi: 10.3969/j.issn.0254-3087.2016.11.012 [8] 易可夫, 王东豪, 万江文.基于优化字典学习算法的压缩数据收集.北京航空航天大学学报, 2016, 42(6): 1203-1209 http://d.old.wanfangdata.com.cn/Periodical/bjhkhtdxxb201606015Yi Ke-Fu, Wang Dong-Hao, Wan Jiang-Wen. Optimized dictionary learning algorithm for compressive data gathering.Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(6): 1203-1209 http://d.old.wanfangdata.com.cn/Periodical/bjhkhtdxxb201606015 [9] 陆婉芸, 王继周, 曹萌.变序字典学习AO-DL的资源三号遥感影像云去除, 测绘学报, 2017, 46(5): 623-630 http://d.old.wanfangdata.com.cn/Periodical/chxb201705011Lu Wan-Yun, Wang Ji-Zhou, Cao-Meng. Cloud removal in ZY-3 remote sensing image based on atoms-reorded dictionary learning AO-DL. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 623-630 http://d.old.wanfangdata.com.cn/Periodical/chxb201705011 [10] Sahoo S K, Makur A. Replacing K-SVD with SGK: Dictionary training for sparse representation of images. In: Proceedings of the 2015 IEEE International Conference on Digital Signal Processing. Singapore, Singapore: IEEE, 2015. 614-617 [11] 练秋生, 石保顺, 陈书贞.字典学习模型、算法及其应用研究进展.自动化学报, 2015, 41(2): 240-260 doi: 10.16383/j.aas.2015.c140252Lian Qiu-Sheng, Shi Bao-Shun, Chen Shu-Zhen. Research advances on dictionary learning models, algorithms and applications. Acta Automatica Sinica, 2015, 41(2): 240-260 doi: 10.16383/j.aas.2015.c140252 [12] Sahoo S K, Makur A. Dictionary training for sparse representation as generalization of K-means clustering. IEEE Signal Processing Letters, 2013, 20(6): 587-590 doi: 10.1109/LSP.2013.2258912 [13] Sahoo S K, Makur A. Image denoising via sparse representations over Sequential Generalization of K-means (SGK). In: Proceedings of the 9th IEEE International Conference on Information, Communications and Signal Processing. Tainan, China: IEEE, 2014. 1-5 [14] Wang Z, Bovik A, Sheikh H, et al. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612 doi: 10.1089-fpd.2009.0394/ -




 下载:
下载: