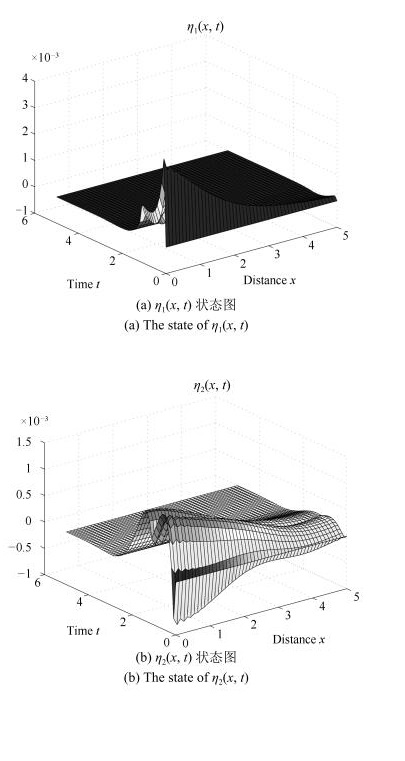
|
[1]
|
Ray W H. Advanced Process Control. New York: McGraw-Hill, 1981.
|
|
[2]
|
Christofides P D. Nonlinear and Robust Control of PDE Systems. Boston: Birkhäuser Boston, 2001.
|
|
[3]
|
Deng H, Li H X, Chen G R. Spectral-approximation-based intelligent modeling for distributed thermal processes. IEEE Transactions on Control Systems Technology, 2005, 13:686-700 doi: 10.1109/TCST.2005.847329
|
|
[4]
|
Padhi R, Ali S F. An account of chronological developments in control of distributed parameter systems. Annual Reviews in Control, 2009, 33:59-68 doi: 10.1016/j.arcontrol.2009.01.003
|
|
[5]
|
Baillieul J. Linearized models for the control of rotating beams. In: Proceedings of the 27th Conference on Decision and Control. Austin, Texas, USA: IEEE, 1989, 3: 1726-1731
|
|
[6]
|
Najar F, Choura S, Abdel-Rahman E M, El-Borgi S, Nayfeh A. Dynamic analysis of variable-geometry electrostatic microactuators. Journal of Micromechanics and Microengineering, 2006, 16(11):2449-2457 doi: 10.1088/0960-1317/16/11/028
|
|
[7]
|
Ly C, Doiron B. Correction:divisive gain modulation with dynamic stimuli in integrate-and-fire neurons. PLoS Computational Biology, 2009, 5(6), DOI: 10.1371/annota-tion/9c4474f6-e58e-41ea-af4b-090bbb86f474
|
|
[8]
|
Luo Y P, Xia W H, Liu G R, Deng F Q. LMI approach to exponential stabilization of distributed parameter control systems with delay. Acta Automatica Sinica, 2009, 35(3):299-304 http://www.ams.org/mathscinet-getitem?mr=2535951
|
|
[9]
|
高存臣, 刘振, 徐瑞萍.一类具有连续分布时滞的分布参数系统的反馈控制.控制与决策, 2013, 28(3):445-450 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201303022Gao Cun-Chen, Liu Zhen, Xu Rui-Ping. Feedback control for a class of distributed Parameter systems with continuous distributed time-delay. Control and Decision, 2013, 28(3):445-450 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201303022
|
|
[10]
|
Xing H L, Li D H, Gao C C, Kao Y G. Delay-independent sliding mode control for a class of quasi-linear parabolic distributed parameter systems with time-varying delay. Journal of the Franklin Institute, 2013, 350(2):397-418 doi: 10.1016/j.jfranklin.2012.12.007
|
|
[11]
|
Yuan K, Alofi A, Cao J D, Al-Mazrooei A, Elaiw A. Synchronization of the coupled distributed parameter system with time delay via proportional-spatial derivative control. Discrete Dynamics in Nature and Society, 2014, 2014: Article No. 418258
|
|
[12]
|
Babaei D, Armaou P A. Adaptive control of chemical distributed parameter systems. IFAC-PapersOnLine, 2015, 48(8):681-686 doi: 10.1016/j.ifacol.2015.09.047
|
|
[13]
|
Demetriou M A. Boundary adaptive synchronization of networked PDEs with adaptive parameter estimators. IFAC-PapersOnLine, 2016, 49(8):242-247 doi: 10.1016/j.ifacol.2016.07.448
|
|
[14]
|
Jiang Z X, Cui B T, Wu W, Zhuang B. Event-driven observer-based control for distributed parameter systems using mobile sensor and actuator. Computers and Mathematics with Applications, 2016, 72(12):2854-2864 doi: 10.1016/j.camwa.2016.10.009
|
|
[15]
|
Wang Z P, Wu H N. Finite dimensional guaranteed cost sampled-data fuzzy control for a class of nonlinear distributed parameter systems. Information Sciences, 2016, 327:21-39 doi: 10.1016/j.ins.2015.08.009
|
|
[16]
|
郭涛, 梁燕军.不确定非线性时滞关联大系统自适应分散容错控制.自动化学报, 2017, 43(3):486-492 http://www.aas.net.cn/CN/abstract/abstract19027.shtmlGuo Tao, Liang Yan-Jun. Adaptive decentralized fault-tolerant control for uncertain nonlinear time-delay large scale systems. Acta Automatica Sinica, 2017, 43(3):486-492 http://www.aas.net.cn/CN/abstract/abstract19027.shtml
|
|
[17]
|
Chen W H, Zhong J C, Zheng W X. Delay-independent stabilization of a class of time-delay systems via periodically intermittent control. Automatica, 2016, 71:89-97 doi: 10.1016/j.automatica.2016.04.031
|
|
[18]
|
Xie T T, Liao X F, Li H Q. Leader-following consensus in second-order multi-agent systems with input time delay:an event-triggered sampling approach. Neurocomputing, 2016, 177:130-135 doi: 10.1016/j.neucom.2015.11.013
|
|
[19]
|
Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory, Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 1994.
|
|
[20]
|
崔宝同, 楼旭阳.时滞分布参数系统理论及其应用.北京:国防工业出版社, 2009. 8-12Cui Bao-Tong, Lou Xu-Yang. Theory and Application of Time-Delay Distributed Parameter System. Beijing:National Defense Industry Press, 2009. 8-12
|




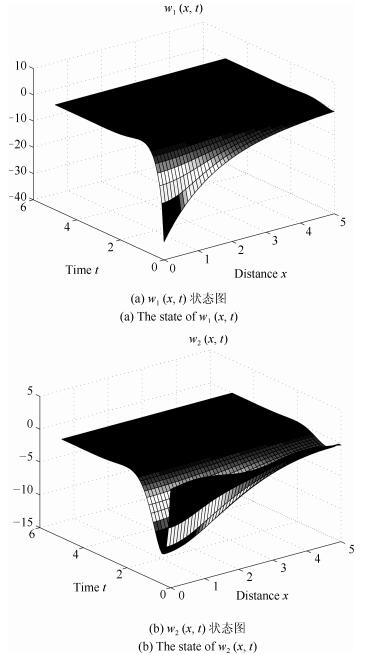
 下载:
下载: