-
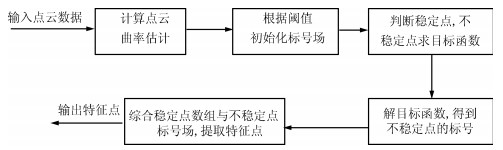
摘要: 为了精确提取点云数据中的特征信息,针对激光扫描获取的三维散乱点云数据,提出一种基于马尔科夫随机场(Markov random field, MRF)的散乱点云特征提取方法.首先,根据散乱点的曲率估计及阈值初始化点标号并判定稳定点,将稳定点标记存储在数组中;然后,将优化不稳定点的标号问题转化为随机场标号的能量函数问题,引用贝叶斯估计求后验概率分布函数及MAP-MRF(Maximum a posteriori-Markov random field)框架归约得到目标函数;最后,根据图割法α-expansion算法,利用标号调整过程中标号集相对能量变化得到不稳定点的最优标号集,将其与存储稳定点的数组综合,根据点标号提取特征点.实验结果表明,该方法简单、高效、无需人工调参,能够依据全局能量的变化自适应提取特征,特征提取结果令人满意.Abstract: In order to extract the feature information of point clouds data accurately, a new method of feature extraction based on Markov random field (MRF) is proposed. First based on scattered point of curvature estimation and the threshold to initialize labels and determine the stability, the stable point marks stored in the array. Second, the problem of optimal unstable label transform to energy function of the label of the airport. By citing Bayesian estimation for posterior probability distribution function and the MAP-MRF (Maximum a posteriori-Markov random field) reduction, objective function is obtained. Finally according to the graph cut algorithm, using label adjustment process label set relative energy changes get optimal labels of unstable set, and the stable storage array synthesis, by labels rapidly extracts feature points. Experimental results show that the proposed method is simple and fast, and does not need manual setting of threshold. According to the change of global energy, the optimal labeling and feature points are extracted.
-
Key words:
- Scattered point cloud /
- feature extraction /
- Markov random field (MRF) /
- label
-
表 1 参数列表
Table 1 The parameter list
参数 取值 作用 α 0.00001 保证两点间势能的正定性 β 8.0 决定先验信息在MRF中所占比重 m 20 m个近邻点, 用来判断稳定点 L 2 标号数, 即分类个数 表 2 含噪声模型特征提取对比表
Table 2 Comparison of feature points extracted with noise model
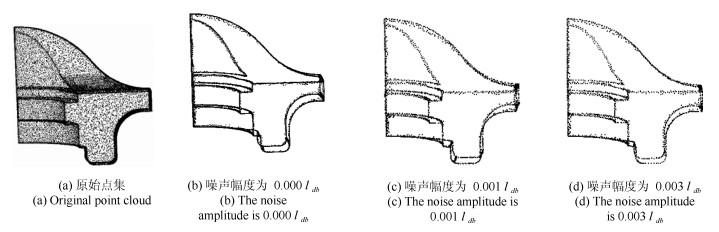
点云名称 采样点数 噪声幅度(ldb) 特征点数 15 115 0.000 2 478 Fandisk 15 115 0.001 1 989 15 115 0.003 1 664 表 3 算法时间效率对比表
Table 3 Comparison table of algorithm time efficiency
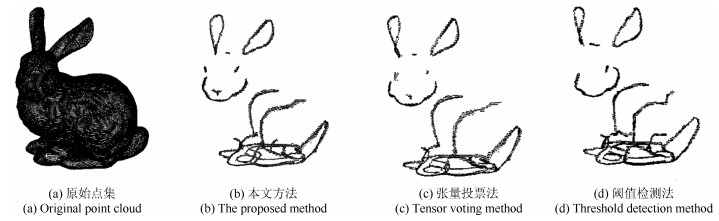
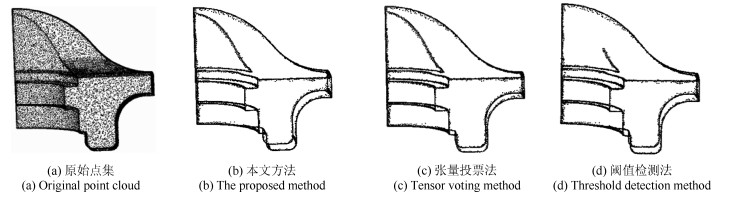
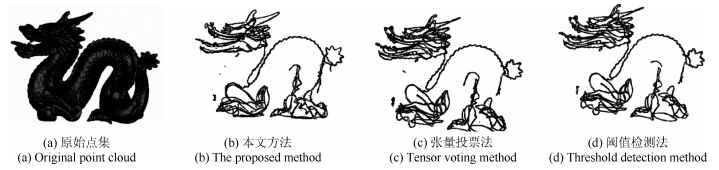
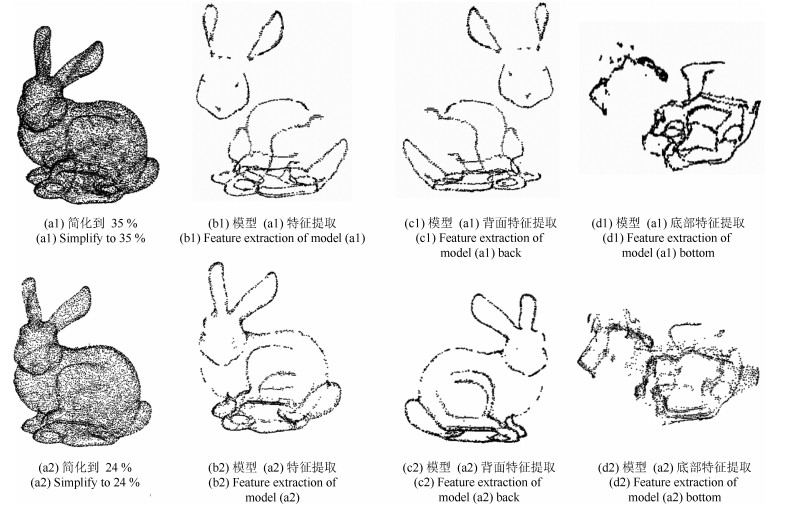
点云名称 采样点数 特征点数 时间耗费(s) 本文算法 张量投票 阈值检测 Bunny 34 863 3 428 6.36 7.34 8.89 Fandisk 15 115 2 478 3.67 3.89 4.16 Dragon 464 869 103 721 189.69 273.56 403.56 -
[1] Daniels J, Ha L K, Ochotta T, Silva C T. Robust smooth feature extraction from point clouds. In:Proceedings of the 2007 IEEE International Conference on Shape Modeling and Applications. Lyon, France:IEEE, 2007. 123-136 http://cn.bing.com/academic/profile?id=2097874565&encoded=0&v=paper_preview&mkt=zh-cn [2] Demarsin K, Vanderstraeten D, Volodine T, Roose D. Detection of closed sharp feature lines in point clouds for reverse engineering applications. In:Proceedings of the 4th International Conference. Pittsburgh, PA, USA:Springer, 2006. 571-577 http://cn.bing.com/academic/profile?id=1546936719&encoded=0&v=paper_preview&mkt=zh-cn [3] 庞旭芳, 庞明勇, 肖春霞.点云模型谷脊特征的提取与增强算法.自动化学报, 2010, 36(8):1073-1083 doi: 10.3724/SP.J.1004.2010.01073Pang Xu-Fang, Pang Ming-Yong, Xiao Chun-Xia. An algorithm for extracting and enhancing valley-ridge features from point sets. Acta Automatica Sinica, 2010, 36(8):1073-1083 doi: 10.3724/SP.J.1004.2010.01073 [4] Tombari F, Salti S, Stefano L D. Performance evaluation of 3D keypoint detectors. International Journal of Computer Vision, 2013, 102(1-3):198-220 doi: 10.1007/s11263-012-0545-4 [5] Pauly M, Keiser R, Gross M. Multi-scale feature extraction on point-sampled surfaces. Computer Graphics Forum, 2003, 22(3):281-289 doi: 10.1111/cgf.2003.22.issue-3 [6] Guo Y L, Bennamoun M, Sohel F, Lu M, Wan J W. 3D object recognition in cluttered scenes with local surface features:a survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11):2270-2287 doi: 10.1109/TPAMI.2014.2316828 [7] Guo Y L, Bennamoun M, Sohel F, Lu M, Wan J W, Kwok N M. A comprehensive performance evaluation of 3D local feature descriptors. International Journal of Computer Vision, 2016, 116(1):66-89 doi: 10.1007/s11263-015-0824-y [8] Ho H T, Gibbins D. Curvature-based approach for multiscale feature extraction from 3D meshes and unstructured point clouds. IET Computer Vision, 2009, 3(4):201-212 doi: 10.1049/iet-cvi.2009.0044 [9] [10] Jia J Y, Tang C K. Tensor voting for image correction by global and local intensity alignment. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(1):36-50 doi: 10.1109/TPAMI.2005.20 [11] Tang C K, Medioni G. Inference of integrated surface, curve and junction descriptions from sparse 3D data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(11):1206-1223 doi: 10.1109/34.730555 [12] 吾守尔·斯拉木, 曹巨明.一种新的散乱点云尖锐特征提取方法.西安交通大学学报, 2012, 46(12):1-5 http://www.cnki.com.cn/Article/CJFDTOTAL-XAJT201212002.htmWushour S, Cao Ju-Ming. An extraction algorithm for sharp feature points from point clouds. Journal of Xi'an Jiaotong University, 2012, 46(12):1-5 http://www.cnki.com.cn/Article/CJFDTOTAL-XAJT201212002.htm [13] 王丽辉, 袁保宗.三维散乱点云模型的特征点检测.信号处理, 2011, 27(6):932-938 http://www.cnki.com.cn/Article/CJFDTOTAL-XXCN201106023.htmWang Li-Hui, Yuan Bao-Zong. Feature point detection for 3D scattered point cloud model. Signal Processing, 2011, 27(6):932-938 http://www.cnki.com.cn/Article/CJFDTOTAL-XXCN201106023.htm [14] Longjiang E, Waseem S, Willis A. Using a MAP-MRF model to improve 3D mesh segmentation algorithms. In:Proceedings of the 2013 IEEE Southeastcon. Jacksonville, FL:IEEE, 2013. 1-7 http://cn.bing.com/academic/profile?id=2030297784&encoded=0&v=paper_preview&mkt=zh-cn [15] Lavoué, Wolf C. Markov random fields for improving 3D mesh analysis and segmentation. In:Proceedings of the 1st Eurographics Conference on 3D Object Retrieval. Switzerland, Switzerland:Eurographics Association Aire-la-Ville, 2008. 25-32 http://cn.bing.com/academic/profile?id=2148126472&encoded=0&v=paper_preview&mkt=zh-cn [16] 卢孝新.基于马尔科夫随机场的三维网格模型分割算法研究[硕士学位论文], 哈尔滨工业大学, 中国, 2010 http://www.doc88.com/p-4307074442697.htmlLu Xiao-Xin. Research on 3D Mesh Segmentation Algorithms Using Markov Random Filed[Master dissertation], Harbin Institute of Technology, China, 2010 http://www.doc88.com/p-4307074442697.html [17] 任然.基于Markov随机场的图像分割方法研究[硕士学位论文], 安徽工业大学, 中国, 2013 http://cdmd.cnki.com.cn/article/cdmd-10360-1013358758.htmRen Ran. Research on Image Segmentation Method Based on Markov Random Field[Master dissertation]. Anhui University of Technology, China, 2013 http://cdmd.cnki.com.cn/article/cdmd-10360-1013358758.htm [18] Wang Xiao-Chao, Liu Xiu-Ping, Li Bao-Jun, Zhang Shao-Guang. Feature detection on point cloud via local reconstruction. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(5):659-665Hoppe H, DeRose T, Duchamp T, McDonald J, Stuetzle W. Surface reconstruction from unorganized points. In:Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA:ACM, 1992. 71-78 [19] 王小超, 刘秀平, 李宝军, 张绍光.基于局部重建的点云特征点提取.计算机辅助设计与图形学学报, 2013, 25(5):659-665 http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198858.htmWang Xiao-Chao, Liu Xiu-Ping, Li Bao-Jun, Zhang ShaoGuang. Feature detection on point cloud via local reconstruction. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(5): 659−665 http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198858.htm [20] Cohen-Steiner D, Morvan J M. Restricted delaunay triangulations and normal cycle. In:Proceedings of the 19th Annual Symposium on Computational Geometry. New York, USA:ACM, 2003. 312-321 http://cn.bing.com/academic/profile?id=2093027094&encoded=0&v=paper_preview&mkt=zh-cn [21] Alexa M, Behr J, Cohen-Or D, Fleishman S, Levin D, Silva C T. Computing and rendering point set surfaces. IEEE Transactions on Visualization and Computer Graphics, 2003, 9(1):3-15 doi: 10.1109/TVCG.2003.1175093 [22] Webber C, Hahmann S, Hagen H. Sharp feature detection in point clouds. In:Proceedings of the 2010 Shape Modeling International Conference. Aix-en-Provence, France:IEEE, 2010. 175-186 http://cn.bing.com/academic/profile?id=2131723805&encoded=0&v=paper_preview&mkt=zh-cn -




 下载:
下载: