|
[1]
|
韩京清. 控制理论——模型论还是控制论. 系统科学与数学, 1989, 9(4):328-335 http://www.cnki.com.cn/Article/CJFDTOTAL-STYS198904005.htmHan Jing-Qing. Control theory, is it a model analysis approach or a direct control approach? Journal of Systems Science and Mathematical Sciences, 1989, 9(4):328-335 http://www.cnki.com.cn/Article/CJFDTOTAL-STYS198904005.htm
|
|
[2]
|
Wu H X, Hu J, Xie Y C. Characteristic model-based all-coefficient adaptive control method and its applications. IEEE Transactions on Systems, Man, and Cybernetics, Part C, 2007, 37(2):213-221 doi: 10.1109/TSMCC.2006.887004
|
|
[3]
|
侯忠生. 再论无模型自适应控制. 系统科学与数学, 2014, 34(10):1182-1191 http://www.cnki.com.cn/Article/CJFDTOTAL-STYS201410005.htmHou Zhong-Sheng. Highlight and perspective on model free adaptive control. Journal of Systems Science and Mathematical Sciences, 2014, 34(10):1182-1191 http://www.cnki.com.cn/Article/CJFDTOTAL-STYS201410005.htm
|
|
[4]
|
侯忠生. 无模型自适应控制的现状与展望. 控制理论与应用, 2006, 23(4):586-592 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY200604018.htmHou Zhong-Sheng. On model-free adaptive control:the state of the art and perspective. Control Theory and Applications, 2006, 23(4):586-592 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY200604018.htm
|
|
[5]
|
侯忠生, 金尚泰. 无模型自适应控制:理论与应用. 北京:科学出版社, 2013.9-11, 46-48, 92-100Hou Zhong-Sheng, Jin Shang-Tai. Model-free Adaptive Control:Theory and Application. Beijing Science Press, 2013.9-11, 46-48, 92-100%
|
|
[6]
|
Guardabassi G O, Savaresi S M. Virtual reference direct design method:an off-line approach to data-based control system design. IEEE Transactions on Automatic Control, 2000, 45(5):954-959 doi: 10.1109/9.855559
|
|
[7]
|
Spall J C. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Transactions on Automatic Control, 1992, 37(3):332-341 doi: 10.1109/9.119632
|
|
[8]
|
侯忠生. 非线性系统参数辨识、自适应控制和无模型学习自适应控制[博士学位论文], 东北大学, 中国, 1994.Hou Zhong-Sheng. Parameter Identification of Nonlinear System, Adaptive Control and Model-free Adaptive Control[Ph.D. dissertation], Northeastern University, China, 1994.
|
|
[9]
|
Hou Z S, Jin S T. A novel data-driven control approach for a class of discrete-time nonlinear systems. IEEE Transactions on Control Systems Technology, 2011, 19(6):1549-1558 doi: 10.1109/TCST.2010.2093136
|
|
[10]
|
Jin S T, Hou Z S, Chi R H. A novel higher-order model-free adaptive control for a class of discrete-time SISO nonlinear systems. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(4):044503 doi: 10.1115/1.4023764
|
|
[11]
|
Hou Z S, Zhu Y M. Controller-dynamic-linearization-based model free adaptive control for discrete-time nonlinear systems. IEEE Transactions on Industrial Informatics, 2013, 9(4):2301-2309 doi: 10.1109/TII.2013.2257806
|
|
[12]
|
Xu D Z, Jiang B, Shi P. A novel model-free adaptive control design for multivariable industrial processes. IEEE Transactions on Industrial Electronics, 2014, 61(11):6391-6398 doi: 10.1109/TIE.2014.2308161
|
|
[13]
|
Hu T S, Lin Z L. Control systems with actuator saturation. Control Engineering. New York:Birkhäuser Basel, 2001.1-15
|
|
[14]
|
Hou Z S, Wang Z. From model-based control to data-driven control:survey, classification and perspective. Information Sciences, 2013, 235:3-35 doi: 10.1016/j.ins.2012.07.014
|
|
[15]
|
Wang L P. Model Predictive Control System Design and Implementation Using Matlab. Berlin:Springer, 2009.110-114
|
|
[16]
|
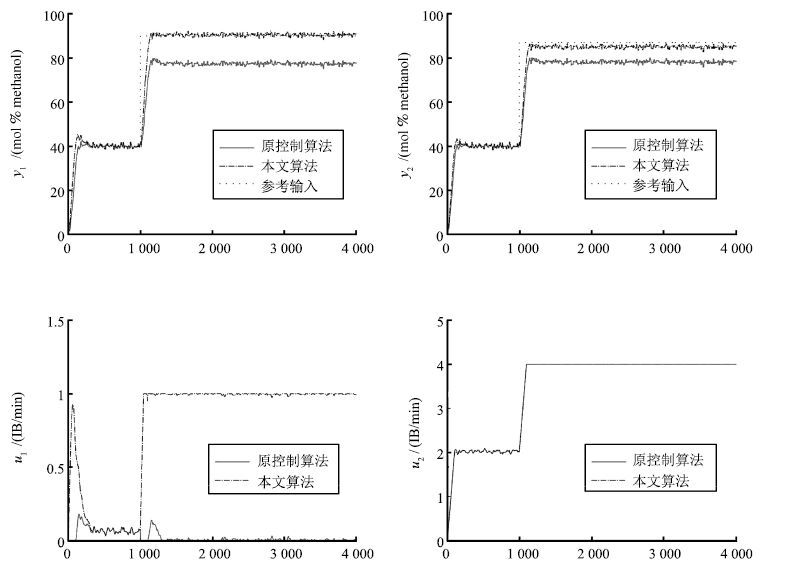
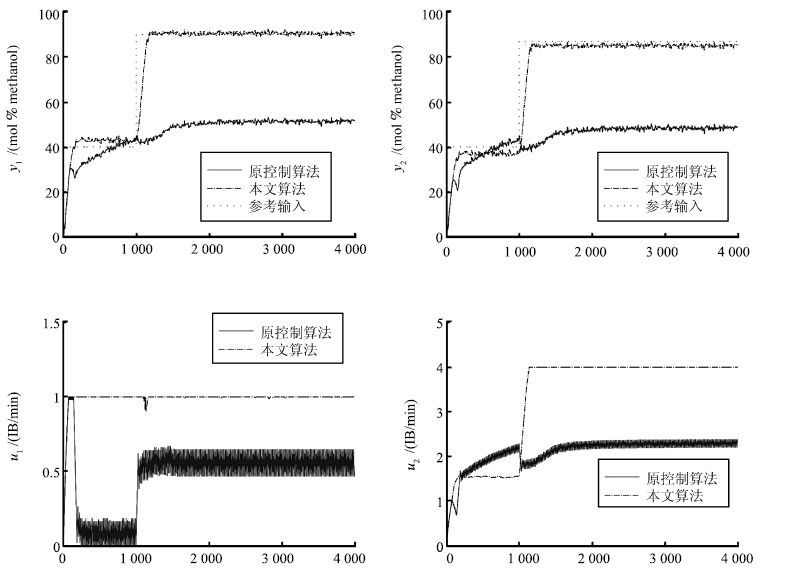
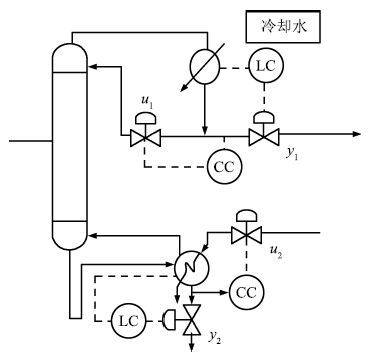
Wood R K, Berry M W. Terminal composition control of a binary distillation column. Chemical Engineering Science, 1973, 28(9):1707-1717 doi: 10.1016/0009-2509(73)80025-9
|




 下载:
下载: