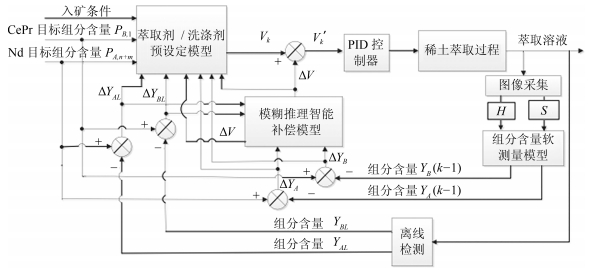
Static Setting and Dynamic Compensation Based Optimal Control for the Flow Rate of the Reagent in CePr/Nd Extraction Process
-
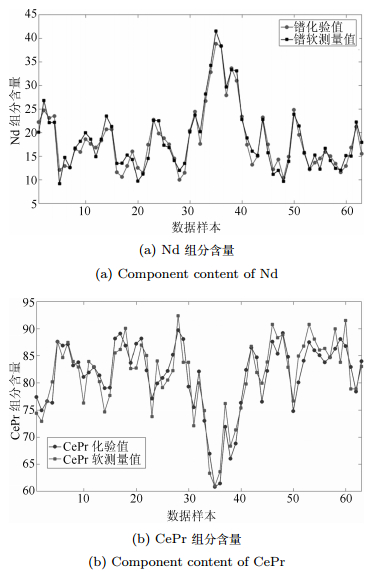
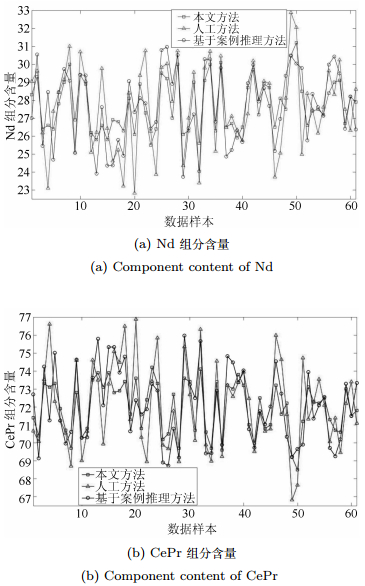
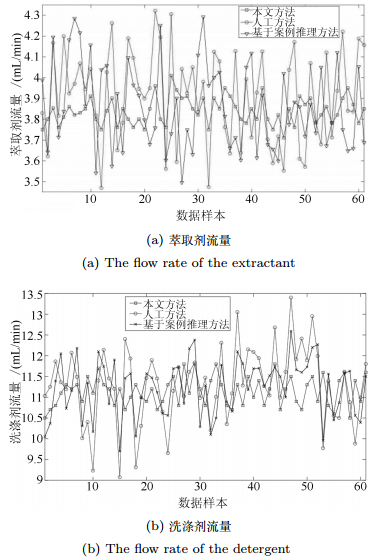
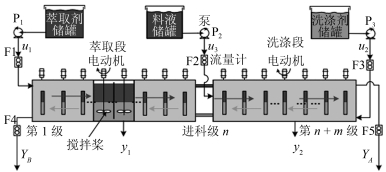
摘要: 针对目前稀土铈镨/钕萃取生产过程人工控制导致生产指标波动大的问题，提出一种新的药剂量优化控制方法.首先针对入矿条件各参数的重要程度不一样，采用特征属性加权的案例推理方法确定药剂量（萃取量和洗涤量）预设定值；然后根据铈镨/钕稀土溶液颜色与组分含量密切相关的特点，采用最小二乘支持向量机（LS-SVM）建立基于稀土溶液颜色的组分含量软测量模型，再根据软测量得到的组分含量与目标组分含量的差值，采用模糊推理技术补偿药剂量预设定值，实现稀土萃取过程组分含量的动态优化控制.试验结果表明本文方法的有效性.Abstract: Manual operation mode easily leads to a large fluctuation of production indices such as component content in the rare earth (RE) cascade extraction industry. A static setting and dynamic compensation based reagent dosage control is proposed to stabilize extraction production running. Firstly, the flow rates of the extractant and the detergent are determined according to feed conditions by case based reasoning (CBR). And then the component content of Nd is measured according to color feature of rare earth solution. The fuzzy reasoning model is used to compensate the flow rates of the extractant and the detergent in order to compliment stable running of the extraction production process according to the difference between the soft-measured value and the given value. Experimental results show the effectiveness of the proposed method.
-
Key words:
- Extraction process /
- color feature /
- reagent dosage /
- case based reasoning (CBR) /
- fuzzy reasoning
1) 本文责任编委 阳春华 -
图 2 萃取量和洗涤量优化控制方案
Fig. 2 Optimal control scheme for the flow rate of the extractant and the detergent
图 3 颜色分量H、S特征值和组分含量相关性分析
Fig. 3 Correlation between color feature and component content
图 5 组分含量误差、组分含量变化差和萃取剂补偿量的隶属度函数
Fig. 5 Membership functions of component content, change error of component content and compensator of the flow rate of the extractant
图 6 基于溶液颜色的组分含量软测量与化验值比较
Fig. 6 Component content by soft sensing based on color feature of rare earth solution and lab test
图 7 人工方法、单模型方法与本文方法的组分含量
Fig. 7 Component content obtained by manual method、CBR based method and the proposed method
图 8 人工方法、案例推理方法与本文方法的萃取量
Fig. 8 Flow rate of the extractant and the detergent consumed by manual method、CBR based method and the proposed method
表 1 语义规则表
Table 1 Semantic rules table
NB NM NS ZO PS PM PB \hline NB PL PL PB PM PM PS ZO NM PL PB PM PS PS ZO NS NS PB PM PS PS ZO NS NM ZO PM PM PS ZO NS NM NM PS PM PS ZO NS NS NM NB PM PS ZO NS NS NM NB NL PB ZO NS NM NM NB NL NL 
下载: 导出CSV
表 2 不同方法建模结果的性能比较
Table 2 Performance comparison of different models
Nd (%) CePr (%) $ {\rm Method} $ $ {\rm RMSE} $ $ {\rm MSE} $ $ {\rm RMSE} $ $ {\rm MSE} $ $ {\rm RBF} $ 0.5829 0.623 0.6243 0.6109 $ {\rm SVM} $ 0.6021 0.528 0.5820 0.652 $ {\rm LSSVM} $ 0.5012 0.4891 0.5391 0.509
下载: 导出CSV
表 3 使用特征参数的隶属度函数
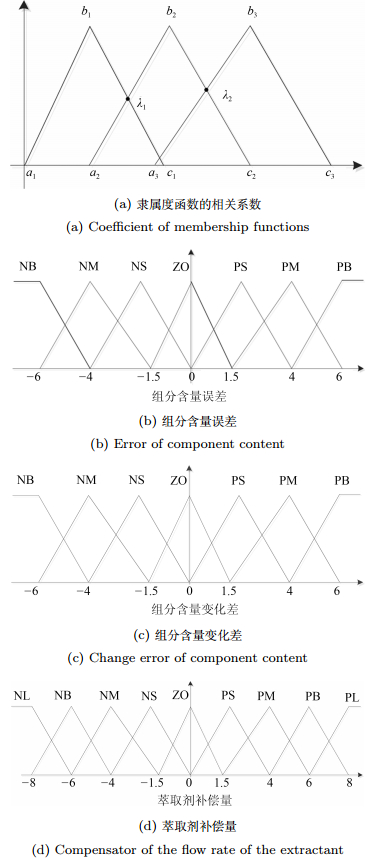
Table 3 Membership functions of the fuzzy logic controller using characteristic parameters
Nd组分含量误差 Nd组分含量变化率 萃取补偿量 NO. $ {a_h} $ $ {b_h} $ $ {c_h} $ $ {a_g} $ $ {b_g} $ $ {c_g} $ $ {a_u} $ $ {b_u} $ $ {c_u} $ 1 -8 -6 -4 -8 -6 -4 -10 -8 -6 2 -6 -4 -1.5 -6 -4 -1.5 -8 -6 -4 3 -4 -1.5 0 -4 -1.5 0 -6 -4 -1.5 4 -1.5 0 1.5 -1.5 0 1.5 -1.5 0 1.5 5 0 1.5 4 0 1.5 4 -4 -1.5 0 6 1.5 4 6 1.5 4 6 0 1.5 4 7 4 6 8 4 6 8 1, 5 4 6 8 $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ 4 6 8 9 $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ $ {\times} $ 6 8 10
下载: 导出CSV
表 4 萃取量和洗涤量消耗统计表(升)
Table 4 Sum of the extractant and detergent comsumend by three methods (L)
人工方法 案例推理方法 本文方法 洗涤量 82.67 82.29 81.54 萃取量 28.63 28.26 27.54
下载: 导出CSV
-
[1] 廖春生, 程福祥, 吴声, 严纯华.串级萃取理论的发展历程及最新进展.中国稀土学报, 2017, 35(1):1-8 http://d.old.wanfangdata.com.cn/Periodical/zgxtxb201701002Liao Chun-Sheng, Cheng Fu-Xiang, Wu Sheng, Yan Chun-Hua. Review and recent progresses on theory of countercurrent extraction. Journal of The Chinese Society of Rare Earths, 2017, 35(1):1-8 http://d.old.wanfangdata.com.cn/Periodical/zgxtxb201701002 [2] 公锡泰, 王欣昌, 阎军, 杨明德, 何培炯.稀土萃取分离过程的在线监测与反馈控制研究.稀土, 1995, 16(2):82-85 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199500558128Gong Xi-Tai, Wang Xin-Chang, Yan Jun, Yang Ming-De, He Pei-Jiong. Study on analysis on-line and feedback control separating rare earth by solvent extraction. Rare Earth, 1995, 16(2):82-85 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199500558128 [3] Giles A E, Aldrich C, Van J S J. Modelling of rare earth solvent extraction with artificial neural nets. Hydrometallurgy, 1996, 43(1-3):241-255 doi: 10.1016/0304-386X(95)00098-2 [4] 贾文君, 柴天佑.稀土串级萃取分离过程的双线性模型及其参数辨识.控制理论与应用, 2006, 23(5):717-723 doi: 10.3969/j.issn.1000-8152.2006.05.010Jia Wen-Jun, Chai Tian-You. Bilinear model of rare earth cascade extraction process and its parameter identification. Control Theory & Applications, 2006, 23(5):717-723 doi: 10.3969/j.issn.1000-8152.2006.05.010 [5] 黄桂文.稀土离子的特征颜色在串级萃取工艺控制中的应用研究.江西冶金, 1996, 16(5):26-27 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600314422Huang Gui-Wen. Color features of rare earth ion based application for cascade extraction process. Jiangxi Metallurgy, 1996, 16(5):26-27 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600314422 [6] Jia J T, Yan C H, Liao C S, Wu S, Wang M W, Li B G. Automation system in rare earths countercurrent extraction processes. Journal of Rare Earths, 2001, 19(1):6-10 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=594e46ca8efcf1b96beaa1547810e0aa [7] Chai T Y, Yang H. Integrated automation system for rare earth countercurrent extraction process. Journal of Rare Earths, 2004, 22(6):752-758 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9f18664fd119d5b28a6fbef1cb0ed8a5 [8] 杨辉, 柴天佑.稀土萃取分离过程的优化设定控制.控制与决策, 2005, 20(4):398-402, 407 doi: 10.3321/j.issn:1001-0920.2005.04.008Yang Hui, Chai Tian-You. Optimal control of rare-earth countercurrent extraction separation process. Control and Decision, 2005, 20(4):398-402, 407 doi: 10.3321/j.issn:1001-0920.2005.04.008 [9] Yang H, Xu F P, Lu R X, Ding Y Q. Component content distribution profile control in rare earth countercurrent extraction process. Chinese Journal of Chemical Engineering, 2015, 23(1):192-198 doi: 10.1016/j.cjche.2014.09.046 [10] 杨辉, 朱凡, 陆荣秀, 张志勇.基于ANFIS模型的Pr/Nd萃取过程预测控制.化工学报, 2016, 67(3):982-990 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hgxb201603047Yang Hui, Zhu Fan, Lu Rong-Xiu, Zhang Zhi-Yong. ANFIS model-based predictive control for Pr/Nd cascade extraction process. CIESC Journal, 2016, 67(3):982-990 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hgxb201603047 [11] Yang H, He L J, Zhang Z Y, Lu R X, Tan C. Multiple model predictive control for component content of CePr/Nd countercurrent extraction process. Information Sciences, 2016, 360:244-255 doi: 10.1016/j.ins.2016.04.031 [12] 杨辉, 高子洁, 陆荣秀.基于稀土离子颜色特征识别的组分含量检测方法.中国稀土学报, 2012, 30(1):108-112 http://d.old.wanfangdata.com.cn/Periodical/zgxtxb201201019Yang Hui, Gao Zi-Jie, Lu Rong-Xiu. Detection method of component content based on rare earth ions color characteristics identification. Journal of the Chinese Society of Rare Earths, 2012, 30(1):108-112 http://d.old.wanfangdata.com.cn/Periodical/zgxtxb201201019 [13] 桂卫华, 阳春华, 陈晓方, 王雅琳.有色冶金过程建模与优化的若干问题及挑战.自动化学报, 2013, 39(3):197-207 http://www.aas.net.cn/CN/abstract/abstract17799.shtmlGui Wei-Hua, Yang Chun-Hua, Chen Xiao-Fang, Wang Ya-Lin. Modeling and optimization problems and challenges arising in nonferrous metallurgical processes. Acta Automatica Sinica, 2013, 39(3):197-207 http://www.aas.net.cn/CN/abstract/abstract17799.shtml [14] 孙备, 张斌, 阳春华, 桂卫华.有色冶金净化过程建模与优化控制问题探讨.自动化学报, 2017, 43(6):880-892 http://www.aas.net.cn/CN/abstract/abstract19067.shtmlSun Bei, Zhang Bin, Yang Chun-Hua, Gui Wei-Hua. Discussion on modeling and optimal control of nonferrous metallurgical purification process. Acta Automatica Sinica, 2017, 43(6):880-892 http://www.aas.net.cn/CN/abstract/abstract19067.shtml [15] 柴天佑, 丁进良, 王宏, 苏春翌.复杂工业过程运行的混合智能优化控制方法.自动化学报, 2008, 34(5):505-515 http://www.aas.net.cn/CN/abstract/abstract13476.shtmlChai Tian-You, Ding Jin-Liang, Wang Hong, Su Chun-Yi. Hybrid intelligent optimal control method for operation of complex industrial processes. Acta Automatica Sinica, 2008, 34(5):505-515 http://www.aas.net.cn/CN/abstract/abstract13476.shtml [16] 柴天佑.复杂工业过程运行优化与反馈控制.自动化学报, 2013, 39(11):1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtmlChai Tian-You. Operational optimization and feedback control for complex industrial processes. Acta Automatica Sinica, 2013, 39(11):1744-1757 http://www.aas.net.cn/CN/abstract/abstract18214.shtml [17] Mántaras R L D, Mcsherry D, Bridge D, Leake D, Smyth B, Craw S, et al. Retrieval, reuse, revision and retention in case-based reasoning. The Knowledge Engineering Review, 2005, 20(3):215-240 doi: 10.1017/S0269888906000646 [18] Cover T, Hart P. Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 1967, 13(1):21-27 doi: 10.1109/TIT.1967.1053964 [19] Castro J L, Navarro M, Sánchez J M, Zurita J M. Introducing attribute risk for retrieval in case-based reasoning. Knowledge-based Systems, 2011, 24(2):257-268 doi: 10.1016/j.knosys.2010.09.002 [20] 赵辉, 严爱军, 王普.基于权重阈值寻优的案例推理分类器特征约简.控制理论与应用, 2015, 32(4):533-539 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201504014Zhao Hui, Yan Ai-Jun, Wang Pu. Feature reduction method based on threshold optimization for case-based reasoning classifier. Control Theory & Applications, 2015, 32(4):533-539 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201504014 [21] Wang H B, Xu A J, AI L X, Tian N Y, Du X. An integrated CBR model for predicting endpoint temperature of molten steel in AOD. ISIJ International, 2012, 52(1):80-86 doi: 10.2355/isijinternational.52.80 [22] 张春晓.案例推理的认知改进策略及学习性能研究[博士学位论文], 北京工业大学, 中国, 2014Zhang Chun-Xiao. Research on the congnitive improvement strategies and learning ability for case-based reasoning[Ph.D. dissertation], Beijing University of Technology, China, 2014 [23] Yan A J, Qian L M, Zhang C X. Memory and forgetting:an improved dynamic maintenance method for case-based reasoning. Information Sciences, 2014, 287:50-60 doi: 10.1016/j.ins.2014.07.040 [24] 陆荣秀, 叶兆斌, 杨辉, 何峰.镨/钕萃取过程组分含量多RBF模型预测.化工学报, 2016, 67(3):974-981 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hgxb201603046Lu Rong-Xiu, Ye Zhao-Bin, Yang Hui, He Feng. Multi-RBF models based prediction of component content for Pr/Nd extraction process. CIESC Journal, 2016, 67(3):974-981 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hgxb201603046 [25] Suykens J A K, de Brabanter J, Lukas L, Vandewalle J. Weighted least squares support vector machines:robustness and sparse approximation. Neurocomputing, 2002, 48(1-4):85-105 doi: 10.1016/S0925-2312(01)00644-0 [26] Ding J L, Chai T Y, Wang H. Offline modeling for product quality prediction of mineral processing using modeling error PDF shaping and entropy minimization. IEEE Transactions on Neural Network, 2011, 22(3):408-419 doi: 10.1109/TNN.2010.2102362 [27] Guo X C, Yang J H, Wu C G, Wang C Y, Liang Y C. A novel LS-SVMs hyper-parameter selection based on particle swarm optimization. Neurocomputing, 2008, 71(16-18):3211-3215 doi: 10.1016/j.neucom.2008.04.027 [28] Ren Y Q, Duan X G, Li H X, Chen C L P. Multi-variable fuzzy logic control for a class of distributed parameter systems. Journal of Process Control, 2013, 23(3):351-358 doi: 10.1016/j.jprocont.2012.12.004 [29] Park Y, Cho H. A fuzzy logic controller for the molten steel level control of strip casting processes. Control Engineering Practice, 2005, 13(7):821-834 doi: 10.1016/j.conengprac.2004.09.006 [30] 徐光宪.稀土.第2版.北京:冶金工业出版社, 1995.Xu Guang-Xian. Rare Earth (Second edition). Beijing:Metallurgical Industry Press, 1995. [31] Zhu J Y, Gui W H, Liu J P, Xu H L, Yang C H. Combined fuzzy based feedforward and bubble size distribution based feedback control for reagent dosage in copper roughing process. Journal of Process Control, 2016, 39:50-63 doi: 10.1016/j.jprocont.2015.12.003 -
图(8) / 表(4)
计量
- 文章访问数: 2453
- HTML全文浏览量: 273
- PDF下载量: 339
- 被引次数: 0
