-
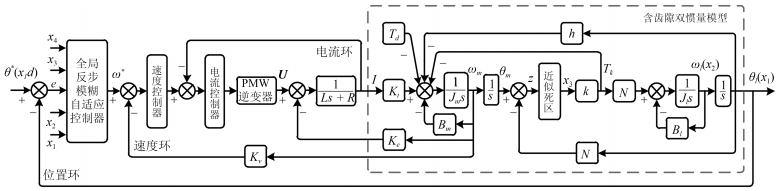
摘要: 针对制导弹药电动舵机伺服系统中存在的齿隙、不确定参数及外部干扰,提出一种基于反步法的全局模糊自适应控制方法.首先,综合考虑上述非线性因素,分析描述齿隙的近似死区模型,建立含齿隙弹载舵机的双惯量机电模型,并将其引入采用"三闭环"结构的伺服系统中,构建非线性系统的状态空间;然后,采用模糊逻辑系统对齿隙等非线性因素进行自适应逼近与补偿控制,通过反步递推构造全系统Lyapunov函数,并运用Lyapunov第二法证明了整个闭环系统最终一致有界.仿真实验表明:较经典PID控制,该方法能更有效地削弱齿隙引起的传动力矩抖振与振荡冲击,既保证了系统的跟踪速度与控制精度,对不确定参数与外部干扰也具有较强的鲁棒性.Abstract: A global fuzzy adaptive control method based on backstepping is proposed for the electro-mechanical actuator servo system of guided projectile, which contains backlash, unknown parameters and external interference. Firstly, with comprehensively considering the above nonlinear factors and analyzing approximate dead zone model that describes backlash, the double inertia electromechanical model with backlash of ammunition actuator was established. And with introducing the electromechanical model into servo system which adopts "three closed-loop" structure, the state space of nonlinear system is constructed. Then, the fuzzy logic system is adopted to adaptively approach, compensate and control nonlinear factors such as backlash. The whole system Lyapunov function is constructed through backstepping, and ultimately uniformly boundedness of the whole closed-loop system is proved by the Lyapunov second method. Finally, the simulation analysis shows that compared with the classical PID control, this method can weaken chattering and oscillating shock caused by backlash more effective, guarantee tracking speed and control accuracy of system, and possess stronger robustness to unknown parameters and external interference.
-
Key words:
- Adaptive control /
- guided projectile /
- electro-mechanical actuator /
- backlash
1) 本文责任编委 刘艳军 -
表 1 控制器参数
Table 1 Parameters of controller
参数 数值 参数 数值 参数 数值 $ K_P $ 2350 $ K_I $ 25 $ K_D $ 5 $ \mu_1 $ 22 $ \mu_2 $ 27 $ \mu_3 $ 15 $ \eta_1 $ 0.1 $ \eta_2 $ 0.1 $ \delta_1 $ 0.01 $ \delta_2 $ 0.01 $ \gamma_1 $ 10 $ \gamma_2 $ 10 -
[1] 邓宏彬, 王超, 赵娜, 徐远清.中小型智能弹药舵机系统设计与应用技术.北京:国防工业出版社, 2016.Deng Hong-Bin, Wang Chao, Zhao Na, Xu Yuan-Qing. Design of Small Ammunition Sheering Gear System. Beijing:National Defend Industry Press, 2016. [2] 奥博连斯基Ю Г, 叶尔马科夫С А, 苏霍鲁科夫Р В[著], 李志, 李明华[译].航空舵机系统设计引论.北京: 航空工业出版社, 2013.ОболvенскийЮГ, ЕрмаковСА, СухоруковРВ [Author], Li Zhi, Li Ming-Hua[Translator]. Introduction to the Design of Aircraft Rudder System. Beijing: Aviation Industry Press, 2013. [3] 朱胜, 孙明轩, 何熊熊.齿隙非线性输入系统的迭代学习控制.自动化学报, 2011, 37(8):1014-1017 http://www.aas.net.cn/CN/abstract/abstract17521.shtmlZhu Sheng, Sun Ming-Xuan, He Xiong-Xiong. Iterative learning control of a class of nonlinear systems with input backlash. Acta Automatica Sinica, 2011, 37(8):1014-1017 http://www.aas.net.cn/CN/abstract/abstract17521.shtml [4] Derugo P, Szabat K. Adaptive neuro-fuzzy PID controller for nonlinear drive system. COMPEL:The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2015, 34(3):792-807 doi: 10.1108/COMPEL-10-2014-0257 [5] 吕帅帅, 林辉, 陈晓雷, 李兵强.弹载电动舵机幂次滑模反演控制.北京理工大学学报, 2016, 36(10):1037-1042 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201610010Lv Shuai-Shuai, Lin Hui, Chen Xiao-Lei, Li Bing-Qiang. Backstepping power fast terminal sliding mode control for missile borne electric rudder. Transactions of Beijing Institute of Technology, 2016, 36(10):1037-1042 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201610010 [6] 赵国峰, 樊卫华, 陈庆伟, 胡维礼.齿隙非线性研究进展.兵工学报, 2006, 27(6):1072-1080 doi: 10.3321/j.issn:1000-1093.2006.06.027Zhao Guo-Feng, Fan Wei-Hua, Chen Qing-Wei, Hu Wei-Li. A survey on backlash nonlinearity. Acta Armamentarii, 2006, 27(6):1072-1080 doi: 10.3321/j.issn:1000-1093.2006.06.027 [7] 王毅, 何朕, 孟范伟.齿隙系统的建模与自振荡分析.电机与控制学报, 2017, 21(3):78-82 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201703011Wang Yi, He Zhen, Meng Fan-Wei. Modeling and limit cycle analysis for systems with backlash. Electric Machines and Control, 2017, 21(3):78-82 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201703011 [8] Lai G Y, Liu Z, Zhang Y, Philip Chen C L. Adaptive fuzzy tracking control of nonlinear systems with asymmetric actuator backlash based on a new smooth inverse. IEEE Transactions on Cybernetics, 2016, 46(6):1250-1262 doi: 10.1109/TCYB.2015.2443877 [9] Shi Z G, Zuo Z Y. Backstepping control for gear transmission servo systems with backlash nonlinearity. IEEE Transactions on Automation Science and Engineering, 2015, 12(2):752-757 doi: 10.1109/TASE.2014.2369430 [10] Tarbouriech S, Queinnec I, Prieur C. Stability analysis and stabilization of systems with input backlash. IEEE Transactions on Automatic Control, 2014, 59(2):488-494 doi: 10.1109/TAC.2013.2273279 [11] Chang K M. Indirect adaptive control for nonlinear systems with system perturbation. Asian Journal of Control, 1999, 1(2):106-115 http://cn.bing.com/academic/profile?id=be8e4b9adf9c51355d2bdfe058092537&encoded=0&v=paper_preview&mkt=zh-cn [12] 李兵强, 陈晓雷, 林辉, 吕帅帅, 马冬麟.机电伺服系统齿隙补偿及终端滑模控制.电工技术学报, 2016, 31(9):162-168 doi: 10.3969/j.issn.1000-6753.2016.09.020Li Bing-Qiang, Chen Xiao-Lei, Lin Hui, Lv Shuai-Shuai, Ma Dong-Lin. Terminal sliding mode control for mechatronic servo systems with backlash nonlinearity compensation. Transactions of China Electrotechnical Society, 2016, 31(9):162-168 doi: 10.3969/j.issn.1000-6753.2016.09.020 [13] Merzouki R, Davila J A, Fridman L, Cadiou J C. Backlash phenomenon observation and identification in electromechanical system. Control Engineering Practice, 2007, 15(4):447-457 doi: 10.1016/j.conengprac.2006.09.001 [14] 杜仁慧, 吴益飞, 陈威, 陈庆伟.考虑齿隙伺服系统的反步自适应模糊控制.控制理论与应用, 2013, 30(2):254-260 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201302018Du Ren-Hui, Wu Yi-Fei, Chen Wei, Chen Qing-Wei. Adaptive backstepping fuzzy control for servo systems with backlash. Control Theory and Applications, 2013, 30(2):254-260 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201302018 [15] 马艳玲, 黄进, 张丹.基于反步自适应控制的伺服系统齿隙补偿.控制理论与应用, 2008, 25(6):1090-1094 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy200806023Ma Yan-Ling, Huang Jin, Zhang Dan. Backlash compensation in servo systems based on adaptive backstepping control. Control Theory and Applications, 2008, 25(6):1090-1094 http://d.old.wanfangdata.com.cn/Periodical/kzllyyy200806023 [16] Wu J, Li J, Chen W S. Practical adaptive fuzzy tracking control for a class of perturbed nonlinear systems with backlash nonlinearity. Information Sciences, 2017, 420:517-531 doi: 10.1016/j.ins.2017.08.085 [17] 郭健, 姚斌, 吴益飞, 陈庆伟.具有输入齿隙的一类非线性不确定系统自适应鲁棒控制.控制与决策, 2010, 25(10):1580-1584 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201010027Guo Jian, Yao Bin, Wu Yi-Fei, Chen Qing-Wei. Adaptive robust control for a class of nonlinear uncertain system with input backlash. Control and Decision, 2010, 25(10):1580-1584 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201010027 [18] Kanellakopoulos I, Kokotovic P V, Morse A S. Systematic design of adaptive controllers for feedback linearizable systems. IEEE Transactions on Automatic Control, 1991, 36(11):1241-1253 doi: 10.1109/9.100933 [19] 陈明俊, 李长红, 杨燕.武器伺服系统工程实践.北京:国防工业出版社, 2013.Chen Ming-Jun, Li Chang-Hong, Yang Yan. Weapons Servo System Engineering Practice. Beijing:National Defend Industry Press, 2013. [20] 虞斐雄, 王永超, 张胜修, 曹立佳, 扈晓祥.输出误差受限的非线性系统模糊反步控制.电光与控制, 2016, 23(9):11-18 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dgykz201609005Yu Fei-Xiong, Wang Yong-Chao, Zhang Sheng-Xiu, Cao Li-Jia, Hu Xiao-Xiang. Fuzzy backstepping control for output error constrained nonlinear systems. Electronics Optics and Control, 2016, 23(9):11-18 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dgykz201609005 [21] 张吉烈, 张化光, 罗艳红, 梁洪晶.基于广义模糊双曲模型的自适应动态规划最优控制设计.自动化学报, 2013, 39(2):142-149 http://www.aas.net.cn/CN/abstract/abstract17824.shtmlZhang Ji-Lie, Zhang Hua-Guang, Luo Yan-Hong, Liang Hong-Jing. Nearly optimal control scheme using adaptive dynamic programming based on generalized fuzzy hyperbolic model. Acta Automatica Sinica, 2013, 39(2):142-149 http://www.aas.net.cn/CN/abstract/abstract17824.shtml [22] 王永超, 张胜修, 曹立佳, 扈晓翔.控制方向未知的输入受限非线性系统自适应模糊反步控制.系统工程与电子技术, 2016, 38(9):2149-2155 http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201609026Wang Yong-Chao, Zhang Sheng-Xiu, Cao Li-Jia, Hu Xiao-Xiang. Adaptive fuzzy backstepping control for nonlinear system with unknown control direction and input saturation. Systems Engineering and Electronics, 2016, 38(9):2149-2155 http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201609026 [23] 同济大学数学系.高等数学.第7版.北京:高等教育出版社, 2014.Department of Mathematics of Tongji University. Higher Mathematics (Seventh edition). Beijing:Higher Education Press, 2014. -



 下载:
下载: