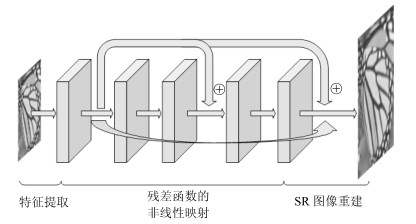
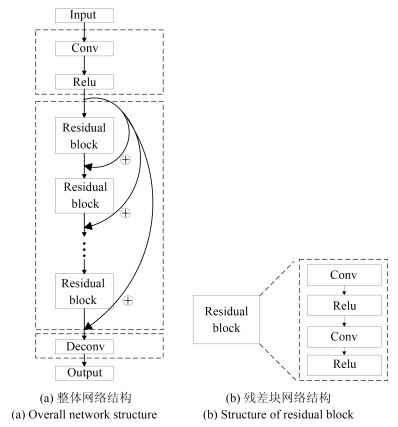
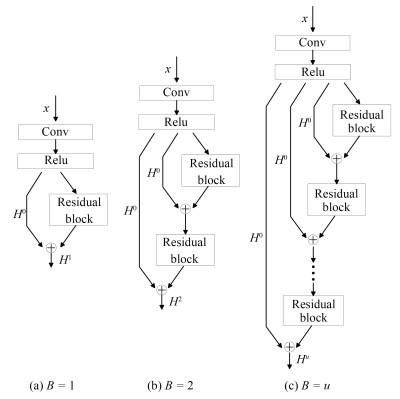
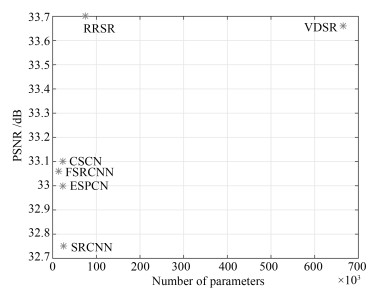
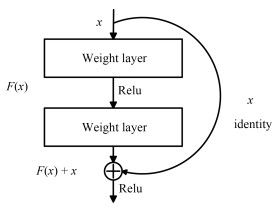
-
摘要: 深度卷积神经网络在单图像超分辨率重建方面取得了卓越成就，但其良好表现通常以巨大的参数数量为代价.本文提出一种简洁紧凑型递归残差网络结构，该网络通过局部残差学习减轻训练深层网络的困难，引入递归结构保证增加深度的同时控制模型参数数量，采用可调梯度裁剪方法防止产生梯度消失/梯度爆炸，使用反卷积层在网络末端直接上采样图像到超分辨率输出图像.基准测试表明，本文在重建出同等质量超分辨率图像的前提下，参数数量及计算复杂度分别仅为VDSR方法的1/10和1/（2n2）.Abstract: Despite the great success in single image super-resolution reconstruction achieved by deep convolutional neural network, the number of the computational parameters is often very large. This paper proposes a concise and compact recursive residual network. The local residual learning method is adopted to mitigate the difficulty of training very deep network, the recursive structure is configured to control the number of model parameters while increasing the model depth, the adjustable gradient clipping strategy is applied to prevent the gradient disappearance/gradient explosion, and a deconvolutional layer is set to directly up sample the image to a super-resolution image at the end of the residual network. According to benchmark tests, in the premise that the same quality super-resolution image is reconstructed, the number of parameters and the computational complexity of the proposed method are reduced to about 1/10 and 1/(2n2) of VDSR, respectively.1) 本文责任编委 王亮
-
图 5 各种U、C组合所构成网络的性能对比图
Fig. 5 The performance of various networks at U and C combinations
图 6 各种SISR方法的×3模型在Set5测试集上的平均PSNR值及参数数量
Fig. 6 Average PSNR and number of parameters on the testset Set5 for scale factor ×3 of various SISR methods
图 7 测试集BSD100中的"img_092"重建结果对比图
Fig. 7 A comparison of the reconstruction results of "img_092" in the testset BSD100
图 8 测试集Set5中的"butterfly"重建对比图
Fig. 8 A comparison of the reconstruction results of "butterfly" in the testset Set5
表 1 不同RRSR组件构成的$\times3$模型在Set5测试集上的平均PSNR值及参数量
Table 1 Average PSNR and number of parameters when different RRSR components are turned on or off, for scale factor $\times3$ on testset Set5
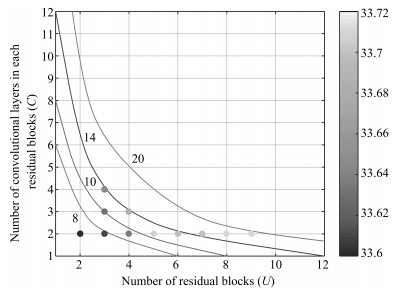
局部残差 递归结构 PSNR (dB) 参数数量($\times10^3$) × × 33.27 371 √ × 33.58 371 √ √ 33.70 39 
下载: 导出CSV
表 2 各种SISR方法的$\times2$, $\times3$和$\times4$模型在测试集Set5、Set14和BSD100上的平均PSNR值与SSIM值
Table 2 Average PSNR/SSIMs of various SISR methords for scale factor $\times2$, $\times3$ and $\times4$ on Set5, Set14 and BSD100
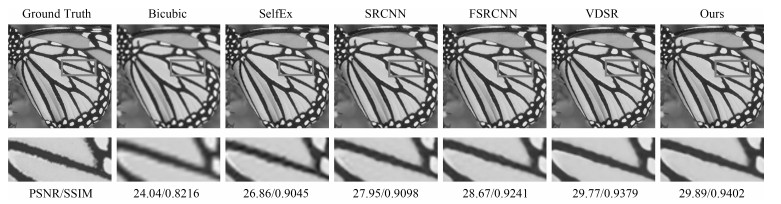
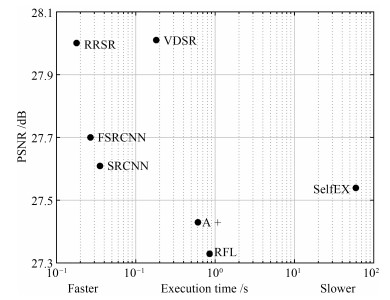
测试集 放大倍数 Bicubic PSNR/SSIM SelfEx PSNR/SSIM SRCNN PSNR/SSIM FSRCNN PSNR/SSIM VDSR PSNR/SSIM RRSR PSNR/SSIM Set5 ×2 33.66/0.9299 36.49/0.9537 36.66/0.9542 37.00/0.9558 37.53/0.9587 37.55/0.9588 Set5 ×3 30.39/0.8682 32.58/0.9093 32.75/0.9090 33.16/0.9140 33.66/0.9213 33.70/0.9208 Set5 ×4 28.42/0.8104 30.31/0.8619 30.48/0.8628 30.71/0.8657 31.35/0.8838 31.32/0.8836 Set14 ×2 30.24/0.8688 32.22/0.9034 32.42/0.9063 32.64/0.9088 33.03/0.9124 33.04/0.9125 Set14 ×3 27.55/0.7742 29.16/0.8196 29.28/0.8209 29.43/0.8242 29.77/0.8314 29.75/0.8307 Set14 ×4 26.00/0.7027 27.40/0.7518 27.49/0.7503 27.60/0.7535 28.01/0.7674 28.00/0.7675 BSD100 ×2 29.56/0.8431 31.18/0.8855 31.36/0.8879 31.51/0.8906 31.90/0.8960 31.91/0.8961 BSD100 ×3 27.21/0.7385 28.29/0.7840 28.41/0.7863 28.52/0.7897 28.82/0.7976 28.78/0.7969 BSD100 ×4 25.96/0.6675 26.84/0.7106 26.90/0.7101 26.97/0.7128 27.29/0.7251 27.25/0.7249
下载: 导出CSV
-
[1] Oktay O, Bai W, Lee M, Guerrero R, Kamnitsas K, Caballero J, et al. Multi-input cardiac image super-resolution using convolutional neural networks. In: Proceedings of the 2016 International Conference on Medical Image Computing and Computer-assisted Intervention. Athens, Greece: Springer, Cham, 2016. 246-254 [2] Luo Y, Zhou L, Wang S, Wang Z Y. Video satellite imagery super resolution via convolutional neural networks. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12):2398-2402 doi: 10.1109/LGRS.2017.2766204 [3] Rasti P, Uiboupin T, Escalera S, Anbarjafari G. Convolutional neural network super resolution for face recognition in surveillance monitoring. In: Proceedings of the 2016 International Conference on Articulated Motion and Deformable Objects. Palma de Mallorca, Spain: Springer, Cham, 2016. 175-184 [4] 陆志芳, 钟宝江.基于预测梯度的图像插值算法.自动化学报, 2018, 44(6):1072-1085 http://www.aas.net.cn/CN/abstract/abstract19297.shtmlLu Zhi-Fang, Zhong Bao-Jiang. Image interpolation with predicted gradients. Acta Automatica Sinica, 2018, 44(6):1072-1085 http://www.aas.net.cn/CN/abstract/abstract19297.shtml [5] 熊娇娇, 卢红阳, 张明辉, 刘且根.基于梯度域的卷积稀疏编码磁共振成像重建.自动化学报, 2017, 43(10):1841-1849 http://www.aas.net.cn/CN/abstract/abstract19159.shtmlXiong Jiao-Jiao, Lu Hong-Yang, Zhang Ming-Hui, Liu Qie-Gen. Convolutional sparse coding in gradient domain for MRI reconstruction. Acta Automatica Sinica, 2017, 43(10):1841-1849 http://www.aas.net.cn/CN/abstract/abstract19159.shtml [6] Dong C, Chen C L, He K M, Tang X O. Learning a deep convolutional network for image super-resolution. In: Proceedings of the 13th European Conference on Computer Vision, Zurich Switzerland: Springer, Cham, 2014. 184-199 [7] Dong C, Chen C L, Tang X O. Accelerating the super-sesolution convolutional neural network. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam, The Netherlands: Springer, Cham, 2016. 391-407 [8] Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1646-1654 [9] Lim B, Son S, Kim H, Nah S, Lee K M. Enhanced deep residual networks for single image super-resolution. In: Proceedings of the 2017 IEEE Computer Vision and Pattern Recognition Workshops. Honolulu, USA: IEEE, 2017. 1132-1140 [10] Lai W S, Huang J B, Ahuja N, Yang M H. Deep laplacian pyramid networks for fast and accurate super-resolution. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 5835-5843 [11] Ledig C, Theis L, Huszar F, Caballero J, Cunningham A, Acosta A, et al. Photo-realistic single image super-resolution using a generative adversarial network. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 105-114 [12] Dong C, Chen C L, He K M, Tang X O. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 38(2):295-307 http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb201709007 [13] Timofte R, De Smet V, Van Gool L. A+: Adjusted anchored neighborhood regression for fast super-resolution. In: Proceedings of the 2015 Asian Conference on Computer Vision. Singapore, Singapore: Springer, Cham. 2015. 111-126 [14] 胡长胜, 詹曙, 吴从中.基于深度特征学习的图像超分辨率重建.自动化学报, 2017, 43(5):814-821 http://www.aas.net.cn/CN/abstract/abstract19059.shtmlHu Chang-Sheng, Zhan Shu, Wu Cong-Zhong. Image super-resolution based on deep learning features. Acta Automatica Sinica, 2017, 43(5):814-821 http://www.aas.net.cn/CN/abstract/abstract19059.shtml [15] Kim J, Lee J K, Lee K M. Deeply-recursive convolutional network for image super-resolution. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, Nevada, USA: IEEE, 2016. 1637-1645 [16] Yang W H, Feng J S, Xie G S, Liu J Y, Guo Z M, Yan S C. Video super-resolution based on spatial-temporal recurrent residual networks. Computer Vision and Image Understanding, 2018, 168:79-92 doi: 10.1016/j.cviu.2017.09.002 [17] LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11):2278-2324 doi: 10.1109/5.726791 [18] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, Nevada, USA: IEEE, 2016. 770-778 [19] Mao X J, Shen C H, Yang Y B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: NIPS, 2016. 2810-2818 [20] Nair V, Hinton G E. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel: ICML, 2010. 807-814 [21] Pascanu R, Mikolov T, Bengio Y. On the difficulty of training recurrent neural networks. In: Proceedings of the 30th International Conference on Machine Learning. Atlanta, USA: ICML, 2013, 28(3): 1310-1318 [22] Perez-Pellitero E, Salvador J, Ruiz-Hidalgo J, Rosenhahn B. PSyCo: Manifold span reduction for super resolution. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1837-1845 [23] Huang Y, Wang W, Wang L. Video super-resolution via bidirectional recurrent convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4):1015-1028 doi: 10.1109/TPAMI.2017.2701380 [24] Yang J C, Wright J, Huang T S, Ma Y. Image super-resolution via sparse representation. IEEE Transactions on Image Processing, 2010, 19(11):2861-2873 doi: 10.1109/TIP.2010.2050625 [25] Schulter S, Leistner C, Bischof H. Fast and accurate image upscaling with super-resolution forests. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 3791-3799 [26] Martin D, Fowlkes C, Tal D, Malik J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings of the 2002 International Conference on Computer Vision. Vancouver, BC, Canada: IEEE, 2002. 416-423 [27] Bevilacqua M, Roumy A, Guillemot C, Alberi Morel M L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In: Proceedings of the 23rd British Machine Vision Conference. Surrey UK: BMVA Press, 2012. 1-10 [28] Zeyde R, Elad M, Protter M. On single image scaleup using sparse-representations. In: Proceedings of the 2012 International Conference on Curves and Surfaces. Avignon, France: Springer, Berlin, Heidelberg, 2012. 711-730 [29] Jia Y Q, Shelhamer E, Donahue J, Karayev S, Long J, Girshick R, et al. Caffe: convolutional architecture for fast feature embedding. In: Proceedings of the 22nd ACM International Conference on Multimedia. New York, USA: ACM, 2014. 675-678 [30] He K M, Zhang X Y, Ren S Q, Sun J. Delving deep into rectifiers: surpassing human-level performance on imagenet classification. In: Proceedings of the 2015 International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 1026-1034 [31] Huang J B, Singh A, Ahuja N. Single image super-resolution from transformed self-exemplars. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 5197-5206 [32] Shi W Z, Caballero J, Huszar F, Totz J, P Aitken A, Bishop R, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1874-1883 [33] Wang Z W, Liu D, Yang J C, Han W, Huang T. Deep networks for image super-resolution with sparse prior. In: Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago, Chile: OALib Journal, 2015. 370-378 [34] Vedaldi A, Lenc K. MatConvNet: convolutional neural networks for MATLAB. In: Proceedings of the 23rd ACM International Conference on Multimedia. New York, USA: ACM, 2015. 689-692 -
图(9) / 表(2)
计量
- 文章访问数: 3249
- HTML全文浏览量: 619
- PDF下载量: 629
- 被引次数: 0
