-
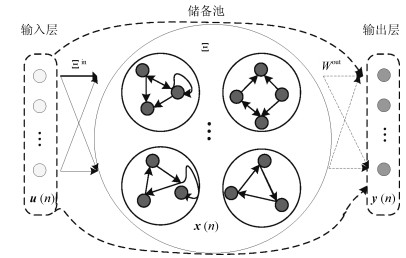
摘要: 针对回声状态网络(Echo state network,ESN)的结构设计问题,提出基于灵敏度分析的模块化回声状态网络修剪算法(Pruning algorithm for modular echo state network,PMESN).该网络由相互独立的子储备池模块构成.首先利用矩阵的奇异值分解(Singular value decomposition,SVD)构造子储备池模块的权值矩阵,并利用分块对角阵原理生成储备池.然后利用子储备池模块输出和相应的输出层权值向量,定义学习残差对于子储备池模块的灵敏度以及网络规模适应度.利用灵敏度大小判断子储备池模块的贡献度,并根据网络规模适应度确定子储备池模块的个数,删除灵敏度低的子模块.在网络的修剪过程中,不需要缩放权值就可以保证网络的回声状态特性.实验结果说明,所提出的算法有效解决了ESN的网络结构设计问题,基本能够确定与样本数据相匹配的网络规模,具有较好的泛化能力和鲁棒性.Abstract: To design the structure of echo state network (ESN), a pruning algorithm for modular echo state network (PMESN) based on sensitivity analysis is proposed in this paper. The reservoir of PMESN is made up of independent sub-reservoir modular networks. The weight matrices of sub-reservoir modular networks are obtained by the singular value decomposition (SVD), and the reservoir is generated by the block diagonal matrix theory. The residual error's sensitivities to the sub-reservoir modular networks are defined by their outputs and weight vectors connecting to the output layer. The significance of the sub-reservoir modular networks is determined by sensitivity. The model scale adaptability is obtained and the sub-reservoir modular networks are sorted by the defined sensitivities. Then, the number of requisite sub-reservoir modular networks is calculated by the model scale adaptability. The redundant sub-reservoir modular networks with smaller sensitivities are deleted. In the pruning process, the echo state property can be guaranteed without posterior scaling of the weights. The simulation results show that the proposed method can design the compact structure of ESN effectively and has better generalization ability and robustness.1) 本文责任编委 鲁仁全
-
表 1 子储备池规模对PMESN性能的影响
Table 1 Influence of sub-reservoir size on PMESN
子储备池
规模训练时间(s) 测试NRMSE 平均值 标准差 3 25.12 8.92×10-3 8.87×10-4 5 27.23 4.56×10-3 4.82×10-4 10 24.35 5.13×10-3 5.48×10-4 15 23.68 6.35×10-3 6.69×10-4 20 22.19 6.98×10-3 6.95×10-4 表 2 储备池初始规模对PMESN性能的影响
Table 2 Influence of initial reservoir size on PMESN
储备池初
始规模训练时间(s) 测试NRMSE 平均值 标准差 100 22.15 8.92 × 10-3 8.78 × 10-4 200 24.54 4.89 × 10-3 4.82 × 10-4 300 26.36 4.72 × 10-3 4.89 × 10-4 400 27.26 4.35 × 10-3 4.48 × 10-4 500 28.39 3.99 × 10-3 4.06 × 10-4 600 32.68 4.82 × 10-3 5.38 × 10-4 表 3 网络规模适应度阈值对PMESN性能的影响
Table 3 Influence of fitness threshold of network size on PMESN
网络规模适 储备池初
始规模测试NRMSE 储备池最
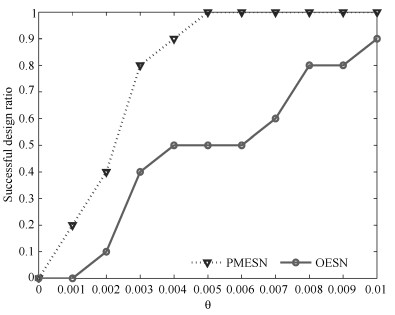
终规模平均值 标准差 1 500 4.12 × 10-3 4.23 × 10-4 432 0.9 500 4.23 × 10-3 4.19 × 10-4 413 0.8 500 4.08 × 10-3 4.29 × 10-4 395 0.7 500 4.21 × 10-3 4.36 × 10-4 382 0.6 500 4.19 × 10-3 4.06 × 10-4 365 0.5 500 4.15 × 10-3 4.13 × 10-4 329 0.4 500 4.02 × 10-3 4.09 × 10-4 298 0.3 500 9.58 × 10-3 9.37 × 10-4 275 0.2 500 5.58 × 10-3 5.62 × 10-4 246 0.1 500 8.69 × 10-3 8.36 × 10-4 213 表 4 基于不同模型的含噪声的Lorenz时间序列预测的参数和仿真结果对比
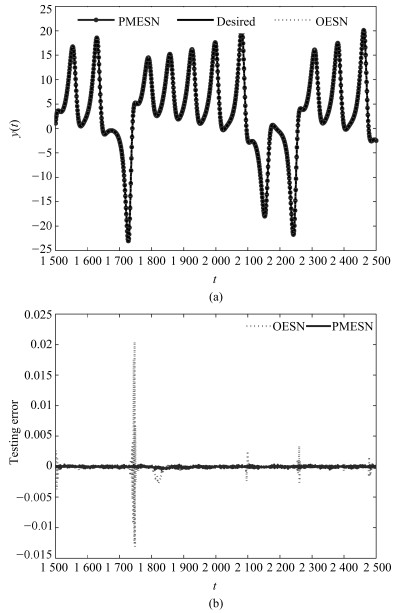
Table 4 Comparison of some parameters and simulation results of different models for Lorenz time series with noise
网络模型 储备池
初始规模储备池
最终规模谱半径 稀疏度 网络规模适
应度阈值训练时间(s) NRMSE 平均值 标准差 PMESN 500 285 0.8500 0.0100 0.4 28.85 4.01 × 10-3 3.64 × 10-4 OESN[1] 500 500 0.8500 0.0500 - 25.32 8.38 × 10-3 6.38 × 10-4 SCR[8] 500 500 0.8000 0.0020 - 22.15 8.28 × 10-3 8.16 × 10-4 DESN[9] 500 500 0.8000 0.0238 - 27.35 9.12 × 10-3 9.43 × 10-4 GESN[6] 50 400 0.9236 0.0200 - 81.35 3.96× 10-3 4.15 × 10-4 SIPA-SCR[11] 500 463 0.8500 0.0020 - 41.39 5.65 × 10-3 5.68 × 10-4 AEESN[13] 500 385 0.8500 0.0500 - 31.39 5.31 × 10-3 5.06 × 10-4 “–”表示原文献中无此参数 表 5 基于不同模型的含噪声的非线性系统辨识的参数和仿真结果对比
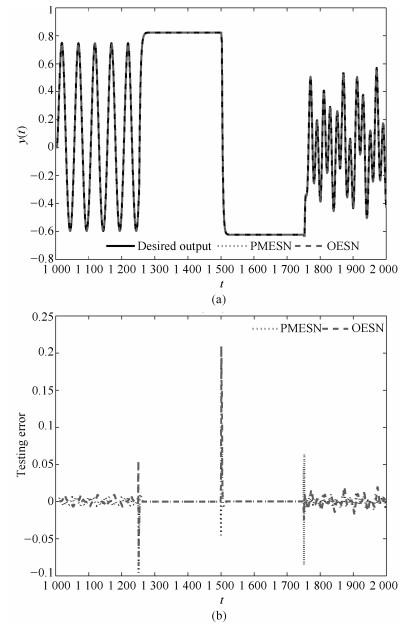
Table 5 Comparison of some parameters and simulation results of different models for nonlinear system identification with noise
网络模型 储备池
初始规模储备池
最终规模谱半径 稀疏度 网络规模适
应度阈值训练时间(s) NRMSE 平均值 标准差 PMESN 500 245 0.8500 0.0100 0.5 39.88 0.0359 0.0020 OESN[1] 500 500 0.8500 0.0500 - 34.46 0.0723 0.0023 SCR[8] 500 500 0.8000 0.0020 - 29.86 0.0692 0.0021 DESN[9] 500 500 0.8000 0.0238 - 36.85 0.0812 0.0022 GESN[6] 50 400 0.9236 0.0200 - 83.69 0.0436 0.0019 SIPA-SCR[11] 500 445 0.8500 0.0020 - 45.66 0.0582 0.0024 AEESN[13] 500 376 0.8500 0.0500 - 37.79 0.0519 0.0018 “–”表示原文献中无此参数 表 6 基于不同模型的出水NH4-N浓度预测的参数和仿真结果对比
Table 6 Comparison of some parameters and simulation results of different models for effluent NH4-N prediction
网络模型 储备池
初始规模储备池
最终规模谱半径 稀疏度 网络规模适
应度阈值训练时间(s) NRMSE 平均值 标准差 PMESN 500 255 0.8500 0.0100 0.4 38.83 0.2039 0.0198 OESN[1] 500 500 0.8500 0.0500 - 32.19 0.3328 0.0232 SCR[8] 500 500 0.8000 0.0020 - 29.86 0.2938 0.0286 DESN[9] 500 500 0.8000 0.0238 - 35.92 0.3426 0.0312 GESN[6] 50 400 0.9236 0.0200 - 91.08 0.2236 0.0022 SIPA-SCR[11] 500 458 0.8500 0.0020 - 44.26 0.2935 0.0301 AEESN[13] 500 365 0.8500 0.0500 - 39.33 0.2899 0.0268 “–”表示原文献中无此参数 -
[1] Jaeger H, Haas H. Harnessing nonlinearity:predicting chaotic systems and saving energy in wireless communication. Science, 2004, 304(5667):78-80 doi: 10.1126/science.1091277 [2] 伦淑娴, 林健, 姚显双.基于小世界回声状态网的时间序列预测.自动化学报, 2015, 41(9):1669-1679 http://www.aas.net.cn/CN/abstract/abstract18740.shtmlLun Shu-Xian, Lin Jian, Yao Xian-Shuang. Time series prediction with an improved echo state network using small world network. Acta Automatica Sinica, 2015, 41(9):1669-1679 http://www.aas.net.cn/CN/abstract/abstract18740.shtml [3] Qiao J F, Wang L, Yang C L, Gu K. Adaptive Levenberg-Marquardt algorithm based echo state network for chaotic time series prediction. IEEE Access, 2018, 6:10720-10732 doi: 10.1109/ACCESS.2018.2810190 [4] Bo Y C, Zhang X. Online adaptive dynamic programming based on echo state networks for dissolved oxygen control. Applied Soft Computing, 2018, 62:830-839 doi: 10.1016/j.asoc.2017.09.015 [5] Skowronski M D, Harris J G. Noise-robust automatic speech recognition using a predictive echo state network. IEEE Transactions on Audio, Speech and Language Processing, 2007, 15(5):1724-1730 doi: 10.1109/TASL.2007.896669 [6] Qiao J F, Li F J, Han H G, Li W J. Growing echo-state network with multiple subreservoirs. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(2):391-404 doi: 10.1109/TNNLS.2016.2514275 [7] Dutoit X, Schrauwen B, Van Campenhout J, Stroobandt D, Van Brussel H, Nuttin M. Pruning and regularization in reservoir computing. Neurocomputing, 2009, 72(7-9):1534-1546 doi: 10.1016/j.neucom.2008.12.020 [8] Rodan A, Tino P. Minimum complexity echo state network. IEEE Transactions on Neural Networks, 2011, 22(1):131-144 doi: 10.1109/TNN.2010.2089641 [9] Xue Y B, Yang L, Haykin S. Decoupled echo state networks with lateral inhibition. Neural Networks, 2007, 20(3):365-376 doi: 10.1016/j.neunet.2007.04.014 [10] 薄迎春, 乔俊飞, 张昭昭.一种具有small world特性的ESN结构分析与设计.控制与决策, 2012, 27(3):383-388 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201203011Bo Ying-Chun, Qiao Jun-Fei, Zhang Zhao-Zhao. Analysis and design on structure of small world property ESN. Control and Decision, 2012, 27(3):383-388 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201203011 [11] Wang H S, Yan X F. Improved simple deterministically constructed cycle reservoir network with sensitive iterative pruning algorithm. Neurocomputing, 2014, 145(18):353-362 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a6e249a7313ddb7f834cda7f77763464 [12] 韩敏, 任伟杰, 许美玲.一种基于L1范数正则化的回声状态网络.自动化学报, 2014, 40(11):2428-2435 http://www.aas.net.cn/CN/abstract/abstract18519.shtmlHan Min, Ren Wei-Jie, Xu Mei-Ling. An improved echo state network via L1-norm regularization. Acta Automatica Sinica, 2014, 40(11):2428-2435 http://www.aas.net.cn/CN/abstract/abstract18519.shtml [13] Xu M L, Han M. Adaptive elastic echo state network for multivariate time series prediction. IEEE Transactions on Cybernetics, 2016, 46(10):2173-2183 doi: 10.1109/TCYB.2015.2467167 [14] Duan H B, Wang X H. Echo state networks with orthogonal pigeon-inspired optimization for image restoration. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(11):2413-2425 doi: 10.1109/TNNLS.2015.2479117 [15] Zhong S S, Xie X L, Lin L, Wang F. Genetic algorithm optimized double-reservoir echo state network for multi-regime time series prediction. Neurocomputing, 2017, 238:191-204 doi: 10.1016/j.neucom.2017.01.053 [16] Wang H S, Yan X F. Optimizing the echo state network with a binary particle swarm optimization algorithm. Knowledge-Based Systems, 2015, 86:182-193 doi: 10.1016/j.knosys.2015.06.003 [17] Jaeger H. The "Echo State" Approach to Analysing and Training Recurrent Neural Networks-with an Erratum Note, GMD Report 148, German National Research Center for Information Technology, Bonn, Germany, 2010. [18] Lorenz E N. Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 1963, 20(2):130-141 doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [19] Lin C J, Chen C H. Identification and prediction using recurrent compensatory neuro-fuzzy systems. Fuzzy Sets and Systems, 2005, 150(2):307-330 doi: 10.1016/j.fss.2004.07.001 [20] Han H G, Lu W, Hou Y, Qiao J F. An adaptive-PSO-based self-organizing RBF neural network. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1):104-117 doi: 10.1109/TNNLS.2016.2616413 [21] Haimi H, Mulas M, Corona F, Vahala R. Data-derived soft-sensors for biological wastewater treatment plants:an overview. Environmental Modelling and Software, 2013, 47:88-107 doi: 10.1016/j.envsoft.2013.05.009 -




 下载:
下载: