-
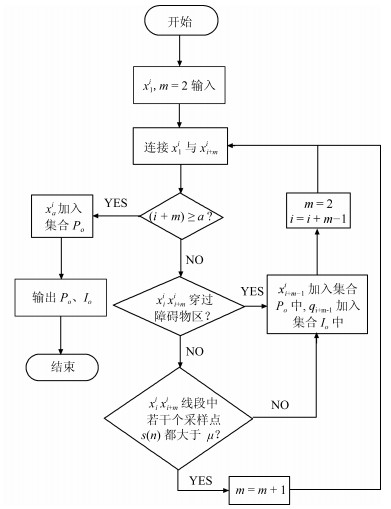
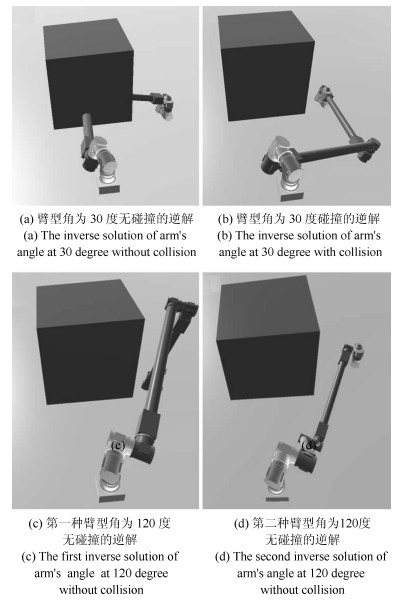
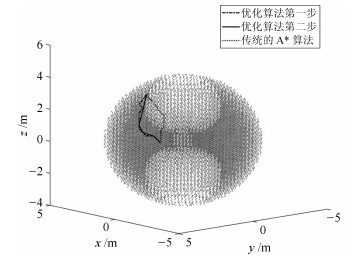
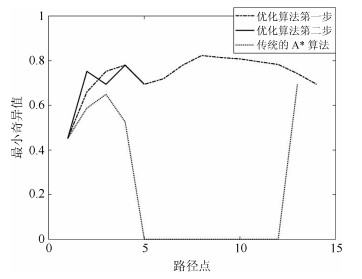
摘要: 针对空间站遥操作7DOF冗余机械臂路径规划的安全性、可靠性问题,提出了基于臂型角逆运动学的优化A*路径规划算法.本文根据臂型角参数化完善了逆运动学方法,得到了32组完备逆解集,增加了路径规划时逆解选择的灵活性;通过臂型角搜索和最小奇异值优化A*路径规划算法,提高机械臂避障、避奇异能力,机械臂操作的灵活性和路径的安全可靠性;同时根据路径优化策略,有效平滑了路径,减少了机械臂的磨损.仿真结果说明了该方法的有效性.Abstract: Aiming at safety and reliability of the space station remote manipulator (SSRMS) type 7DOF redundant manipulator's path planning, an optimized A* path planning algorithm is proposed based on the inverse kinematics of arm angle. This paper improves the method of inverse solution based parameterized arm angle, and obtains 32 sets of complete inverse solutions, which increases flexibility of inverse solution selection in path planning, optimizes the method of A* path planning based on arm angle search and minimum singular value, which increases ability to avoid obstacle and singularity, flexibility of manipulator operation, safety and reliability. At the same time, according to the path optimization strategy, the path is effectively smoothed to reduce the wear of the manipulator. The simulation shows the effectiveness of the method.
-
Key words:
- Redundant manipulator /
- arm angle /
- inverse kinematics /
- A* path planning algorithm
1) 本文责任编委 倪茂林 -
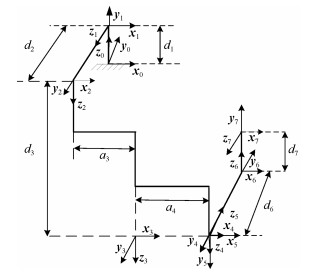
表 1 机械臂D-H参数
Table 1 The D-H parameters of manipulator
杆$i$ ${{\theta }_{i}} \, ({}^\circ )$ ${{\alpha }_{i}} \, ({}^\circ )$ ${{a}_{i}} \, (\text{m)}$ ${{d}_{i}}\, (\text{m)}$ 1 0 90 0 ${{d}_{1}}$ 2 0 90 0 ${{d}_{2}}$ 3 0 0 ${{a}_{3}}$ ${{d}_{3}}$ 4 0 0 ${{a}_{4}}$ ${{d}_{4}}$ 5 0 90 0 ${{d}_{5}}$ 6 0 90 0 ${{d}_{6}}$ 7 0 90 0 ${{d}_{7}}$ 表 2 仿真机械臂D-H参数
Table 2 Simulation parameter of manipulator's DH
杆$i$ ${{\theta }_{i}} ({}^\circ )$ ${{\alpha }_{i}} ({}^\circ )$ ${{a}_{i}} (\text{m)}$ ${{d}_{i}} (\text{m)}$ 1 90 90 0 0.25 2 90 90 0 0.25 3 90 0 2.0 0.6 4 180 0 2.0 0 5 90 90 0 0 6 0 90 0 0.25 7 0 90 0 0.35 -
[1] 梁斌, 徐文福, 李成.地球静止轨道在轨服务技术研究现状与发展趋势.宇航学报, 2010, 31(1):1-13 doi: 10.3873/j.issn.1000-1328.2010.01.001Liang Bin, Xu Wen-Fu, Li Cheng. The status and prospect of orbital servicing in the Geostationary orbit. Journal of Astronautics, 2010, 31(1):1-13 doi: 10.3873/j.issn.1000-1328.2010.01.001 [2] Coleshill E, Oshinowo L, Rembala R, Bina B, Rey D, Sindelar S. Dextre:improving maintenance operations on the International Space Station. Acta Astronautica, 2009, 64(9-10):869-874 doi: 10.1016/j.actaastro.2008.11.011 [3] Boumans R, Heemskerk C. The European robotic arm for the International Space Station. Robotics and Autonomous Systems, 1998, 23(1-2):17-27 doi: 10.1016/S0921-8890(97)00054-7 [4] Shimizu M, Kakuya H, Yoon W K, Kitagaki K, Kosuge K. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution. IEEE Transactions on Robotics, 2008, 24(5):1131-1142 doi: 10.1109/TRO.2008.2003266 [5] 方承, 丁希仑.面向人臂三角形动作基元的拟人臂运动学.机器人, 2012, 34(3):257-264 http://d.old.wanfangdata.com.cn/Periodical/jqr201203001Fang Cheng, Ding Xi-Lun. Anthropomorphic arm kinematics oriented to movement primitive of human arm triangle. Robot, 2012, 34(3):257-264 http://d.old.wanfangdata.com.cn/Periodical/jqr201203001 [6] Singh G K, Claassens J. An analytical solution for the inverse kinematics of a redundant 7DOF manipulator with link offsets. In:Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan, China:IEEE, 2010. 2976-2986 [7] Yu C, Jin M H, Liu H. An analytical solution for inverse kinematic of 7-DOF redundant manipulators with offset-wrist. In:Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation. Chengdu, China:IEEE, 2012. 92-97 https://ieeexplore.ieee.org/document/6282813/ [8] Crane C D III, Duffy J, Carnahan T. A kinematic analysis of the Space Station Remote Manipulator system (SSRMS). Journal of Robotic Systems, 1991, 8(5):637-658 doi: 10.1002/rob.v8:5 [9] 徐文福, 张金涛, 闫磊, 王志英.偏置式冗余空间机械臂逆运动学求解的参数化方法.宇航学报, 2015, 36(1):33-39 doi: 10.3873/j.issn.1000-1328.2015.01.005Xu Wen-Fu, Zhang Jin-Tiao, Yan Lei, Wang Zhi-Ying. Parameterized inverse kinematics resolution method for a redundant space manipulator with link offset. Journal of Astronautics, 2015, 36(1):33-39 doi: 10.3873/j.issn.1000-1328.2015.01.005 [10] Kreutz-Delgado K, Long M, Seraji H. Kinematic analysis of 7-DOF manipulators. The International Journal of Robotics Research, 1992, 11(5):469-481 doi: 10.1177/027836499201100504 [11] Tevatia G, Schaal S. Inverse kinematics for humanoid robots. In:Proceedings of the 2000 IEEE International Conference on Robotics and Automation. San Francisco, CA, USA:IEEE, 2000. 294-299 https://www.researchgate.net/publication/3847239_Inverse_kinematics_for_humanoid_robots [12] 闫磊. 拟人机器人参数化逆运动学及在轨装配的协调规划研究[硕士学位论文], 哈尔滨工业大学, 中国, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015983066.htmYan Lei. Parameterized Inverse Kinematics and Coordinated Planning of Anthropomorphic Robotic Arm for On-orbit Assembly[Master thesis], Harbin Institute of Technology, China, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015983066.htm [13] Baghli F Z, El Bakkali L, Lakhal Y. Optimization of arm manipulator trajectory planning in the presence of obstacles by ant colony algorithm. Procedia Engineering, 2017, 181:560-567 doi: 10.1016/j.proeng.2017.02.434 [14] 郭勇强. 空间大型机械臂关节控制系统及轨迹规划研究[博士学位论文], 哈尔滨工业大学, 中国, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10213-1013035329.htmGuo Yong-Qiang. Research on Joint Control System and Trajectory Planning for Large Manipulator[Ph.D. dissertation], Harbin Institute of Technology, China, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10213-1013035329.htm [15] 汪首坤, 邸智, 王军政, 郭俊杰.基于A*改进算法的机械臂避障路径规划.北京理工大学学报, 2011, 31(11):1302-1306 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201111010Wang Shou-Kun, Di Zhi, Wang Jun-Zheng, Guo Jun-Jie. Path planning method for manipulator to avoid obstacle based on advanced A* algorithm. Transactions of Beijing Institute of Technology, 2011, 31(11):1302-1306 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201111010 [16] Yao J F, Lin C, Xie X B, Wang A J, Hung C C. Path planning for virtual human motion using improved A* star algorithm. In:Proceedings of the Seventh International Conference on Information Technology:New Generations. Las Vegas, NV, USA:IEEE, 2010. 1154-1158 https://www.researchgate.net/publication/220841276_Path_Planning_for_Virtual_Human_Motion_Using_Improved_A_Star_Algorithm [17] 贾庆轩, 陈钢, 孙汉旭, 郑双奇.基于A*算法的空间机械臂避障路径规划.机械工程学报, 2010, 46(13):109-115 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201013015Jia Qing-Xuan, Chen Gang, Sun Han-Xu, Zheng Shuang-Qi. Path planning for space manipulator to avoid obstacle based on A* algorithm. Journal of Mechanical Engineering, 2010, 46(13):109-115 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201013015 [18] Ge J X, Sun F C, Liu C F. PRT-GD:an efficient rapidly-exploring random tree approach with goal directionality for redundant manipulator path planning. In:Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics. Qingdao, China:IEEE, 2016. 1983-1988 https://www.researchgate.net/publication/314202932_RRT-GD_An_efficient_rapidly-exploring_random_tree_approach_with_goal_directionality_for_redundant_manipulator_path_planning [19] 王瞾, 胡立生.基于深度Q学习的工业机械臂路径规划方法.化工自动化及仪表, 2018, 45(2):141-145, 171 doi: 10.3969/j.issn.1000-3932.2018.02.012Wang Zhao, Hu Li-Sheng. Industrial manipulator path planning based on deep Q-learning. Control and Instruments in Chemical Industry, 2018, 45(2):141-145, 171 doi: 10.3969/j.issn.1000-3932.2018.02.012 [20] 宗成星, 陆亮, 雷新宇, 赵萍.一种基于A*算法的空间多自由度机械臂路径规划方法.合肥工业学报(自然科学版), 2017, 40(2):164-168 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hfgydxxb201702005Zong Cheng-Xing, Lu Liang, Lei Xin-Yu, Zhao Ping. A path planning approach for multi-DOF spatial manipulator via A* algorithm. Journal of Hefei University of Technology, 2017, 40(2):164-168 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hfgydxxb201702005 [21] 徐文福, 梁斌, 刘宇, 李成, 强文义.一种新的PUMA类型机器人奇异回避算法.自动化学报, 2008, 34(6):670-675 http://www.aas.net.cn/CN/abstract/abstract17890.shtmlXu Wen-Fu, Liang Bin, Liu Yu, Li Cheng, Qiang Wen-Yi. A novel approach to avoid singularities of PUMA-type manipulators. Acta Automatica Sinica, 2008, 34(6):670-675 http://www.aas.net.cn/CN/abstract/abstract17890.shtml [22] 张浩杰, 龚建伟, 姜岩, 熊光明, 陈慧岩.基于变维度状态空间的增量启发式路径规划方法研究.自动化学报, 2013, 39(10):1602-1610 http://www.aas.net.cn/CN/abstract/abstract18197.shtmlZhang Hao-Jie, Gong Jian-Wei, Jiang Yan, Xiong Guang-Ming, Chen Hui-Yan. Research on incremental heuristic path planner with variable dimensional state space. Acta Automatica Sinica, 2013, 39(10):1602-1610 http://www.aas.net.cn/CN/abstract/abstract18197.shtml [23] 霍伟.机器人动力学与控制.第2版.北京:高等教育出版社, 2005. 5-46Huo Wei. Robot Dynamics and Control (Second edition). Beijing:Higher Education Press, 2005. 5-46 [24] Craig J J. Introduction to Robotics:Mechanics and Control (Third edition). America, 2005 -




 下载:
下载: