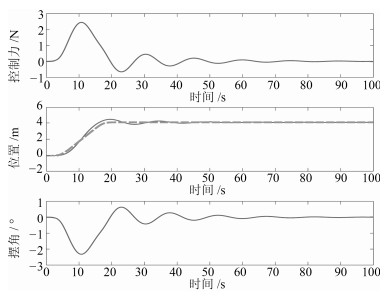
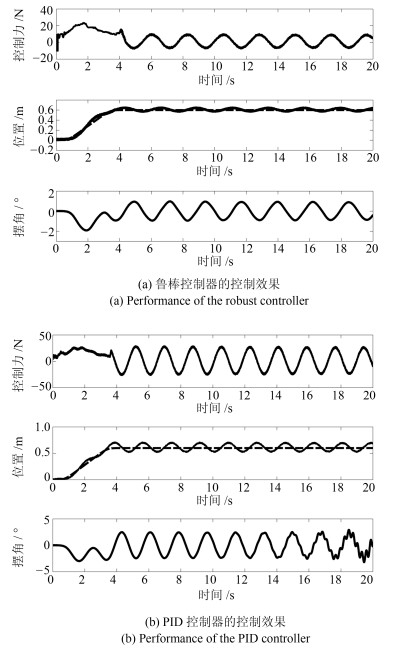
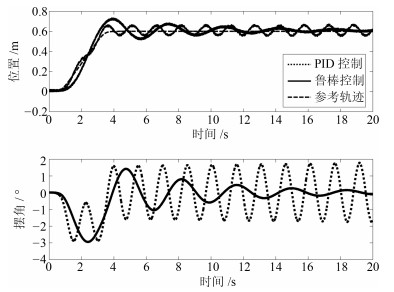
|
[1]
|
Richard J P. Time-delay systems:an overview of some recent advances and open problems. Automatica, 2003, 39(10):1667-1694 doi: 10.1016/S0005-1098(03)00167-5
|
|
[2]
|
Wu M, He Y, She J H. Stability Analysis and Robust Control of Time-Delay Systems. Beijing, China:Science Press, 2010.
|
|
[3]
|
Bresch-Pietri D, Kristic M. Adaptive trajectory tracking despite unknown input delay and plant parameters. Automatica, 2009, 45(9):2074-2081 doi: 10.1016/j.automatica.2009.04.027
|
|
[4]
|
Huang C, Yu C B. Global adaptive controller for linear systems with unknown input delay. IEEE Transactions on Automatic Control, 2017, 62(12):6589-6594 doi: 10.1109/TAC.2017.2714858
|
|
[5]
|
Cai X S, Bekiaris-Liberis N, Kristic M. Input-to-state stability and inverse optimality of linear time-varying-delay predictor feedbacks. IEEE Transactions on Automatic Control, 2018, 63(1):233-240 doi: 10.1109/TAC.2017.2722104
|
|
[6]
|
杜鑫, 丁大伟.基于平衡截断法的离散时间线性时滞系统的低频域模型降阶.自动化学报, 2015, 41(10):1825-1830 http://www.aas.net.cn/CN/abstract/abstract18756.shtmlDu Xin, Ding Da-Wei. Model order reduction of linear delay systems over low-frequency ranges via balanced truncation based approach. Acta Automatica Sinica, 2015, 41(10):1825-1830 http://www.aas.net.cn/CN/abstract/abstract18756.shtml
|
|
[7]
|
Wang Y E, Sun M X, Wu B W. Lyapunov-Krasovskii functionals for input-to-state stability of switched non-linear systems with time-varying input delay. IET Control Theory & Applications, 2015, 9(11):1717-1722 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=efee368cd30e706d7427c8413e3ec956
|
|
[8]
|
Hu X X, Wu L G, Si X S, Xu B. Adaptive sliding mode control of non-linear non-minimum phase system with input delay. IET Control Theory & Applications, 2017, 11(8):1153-1161 http://cn.bing.com/academic/profile?id=591ed2b329c09c5911638bf89b8f25f5&encoded=0&v=paper_preview&mkt=zh-cn
|
|
[9]
|
黄亚欣, 张星慧, 蒋蒙蒙.带有输入和状态时滞的高阶非线性前馈系统的自适应控制.自动化学报, 2017, 43(7):1273-1279 http://www.aas.net.cn/CN/abstract/abstract19101.shtmlHuang Ya-Xin, Zhang Xing-Hui, Jiang Meng-Meng. Adaptive control for high-order nonlinear feedforward systems with input and state delays control. Acta Automatica Sinica, 2017, 43(7):1273-1279 http://www.aas.net.cn/CN/abstract/abstract19101.shtml
|
|
[10]
|
文新宇.一类含输入时滞非线性系统的干扰观测器控制.自动化学报, 2014, 40(9):1882-1888 http://www.aas.net.cn/CN/abstract/abstract18457.shtmlWen Xin-Yu. Disturbance observer based control for a class of nonlinear systems with input time-delay. Acta Automatica Sinica, 2014, 40(9):1882-1888 http://www.aas.net.cn/CN/abstract/abstract18457.shtml
|
|
[11]
|
Sharma N, Bhasin Q, Wang Q, Dixon W E. Predictor-based control for an uncertain Euler-Lagrange system with input delay. In:Proceedings of the 2010 American Control Conference (ACC). Baltimore, USA:IEEE, 2010. 1422-1427
|
|
[12]
|
Fischer N, Dani A, Sharma N, Dixon W E. Saturated control of an uncertain nonlinear system with input delay. Automatica, 2013, 49(6):1741-1747 doi: 10.1016/j.automatica.2013.02.013
|
|
[13]
|
Liu L, Cao J D, Qian C. pth moment exponential input-to-state stability of delayed recurrent neural networks with Markovian switching via vector Lyapunov function. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(7):3152-3163 https://ieeexplore.ieee.org/document/7970146/
|
|
[14]
|
Chen B, Liu X P, Tong S C, Chong L. Observer-based stabilization of T-S fuzzy systems with input delay. IEEE Transactions on Fuzzy Systems, 2008, 16(3):652-663 doi: 10.1109/TFUZZ.2007.903329
|
|
[15]
|
Zavari K, Pipeleers G, Swevers J. Gain-scheduled controller design:illustration on an overhead crane. IEEE Transactions on Industrial Electronics, 2014, 61(7):3713-3718 doi: 10.1109/TIE.2013.2270213
|
|
[16]
|
Boschetti G, Caracciolo R, Richiedei D, Trevisani A. Moving the suspended load of an overhead crane along a pre-specified path:a non-time based approach. Robotics and Computer-Integrated Manufacturing, 2014, 30(3):256-264 doi: 10.1016/j.rcim.2013.10.004
|
|
[17]
|
Sun N, Fang Y C, Chen H, Lu B. Amplitude-saturated nonlinear output feedback antiswing control for underactuated cranes with double-pendulum cargo dynamics. IEEE Transactions on Industrial Electronics, 2017, 64(3):2135-2146 doi: 10.1109/TIE.2016.2623258
|
|
[18]
|
Sun N, Fang Y C, Zhang X B, Yuan Y. Transportation task-oriented trajectory planning for underactuated overhead cranes using geometric analysis. IET Control Theory & Applications, 2012, 6(10):1410-1423 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f85390ec56775dfe30914f3443cc302a
|
|
[19]
|
胡洲, 王志胜, 甄子洋.带输入饱和的欠驱动吊车非线性信息融合控制.自动化学报, 2014, 40(7):1522-1527 http://www.aas.net.cn/CN/abstract/abstract18422.shtmlHu Zhou, Wang Zhi-Sheng, Zhen Zi-Yang. Nonlinear information fusion control for underactuated cranes with input saturation. Acta Automatica Sinica, 2014, 40(7):1522-1527 http://www.aas.net.cn/CN/abstract/abstract18422.shtml
|
|
[20]
|
Sano H, Ohishi K, Kaneko T, Mine H. Anti-sway crane control based on dual state observer with sensor-delay correction. In:Proceedings of the 11th IEEE International Workshop on Advanced Motion Control. Nagaoka, Niigata, Japan:IEEE, 2010. 679-684
|
|
[21]
|
Dey R, Sinha N, Chaubey P, Ghosh S, Ray G. Active sway control of a single pendulum gantry crane system using output-delayed feedback control technique. In:Proceedings of the 11th International Conference on Control, Automation, Robotics and Vision. Singapore:IEEE, 2010. 532-536
|
|
[22]
|
Nayfeh N A, Baumann W T. Nonlinear analysis of time-delay position feedback control of container cranes. Nonlinear Dynamics, 2008, 53(1-2):75-88 doi: 10.1007/s11071-007-9297-z
|
|
[23]
|
Zhao Y, Gao H J. Fuzzy-model-based control of an overhead crane with input delay and actuator saturation. IEEE Transactions on Fuzzy Systems, 2012, 20(1):181-186 doi: 10.1109/TFUZZ.2011.2164083
|
|
[24]
|
何博, 方勇纯, 刘海亮, 孙宁.桥式起重机精准定位在线轨迹规划方法设计及应用.控制理论与应用, 2016, 33(10):1352-1358 doi: 10.7641/CTA.2016.60312He Bo, Fang Yong-Chun, Liu Hai-Liang, Sun Ning. Precise positioning online trajectory planner design and application for overhead cranes. Control Theory & Applications, 2016, 33(10):1352-1358 doi: 10.7641/CTA.2016.60312
|
|
[25]
|
De Queiroz M, Hu J, Dawson D M, Burg T, Donepudi S R. Adaptive position/force control of robot manipulators without velocity measurements:theory and experimentation. IEEE Transactions on Systems, Man and Cybernetics, Part B (Cybernetics), 1997, 27(5):796-809 doi: 10.1109/3477.623233
|
|
[26]
|
Dixon W E, De Queiroz M S, Zhang F, Dawson D M. Tracking control of robot manipulators with bounded torque inputs. Robotica, 1999, 17(2):121-129 doi: 10.1017/S0263574799001228
|
|
[27]
|
Corless M, Leitmann G. Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems. IEEE Transactions on Automatic Control, 1981, 26(5):1139-1144 doi: 10.1109/TAC.1981.1102785
|




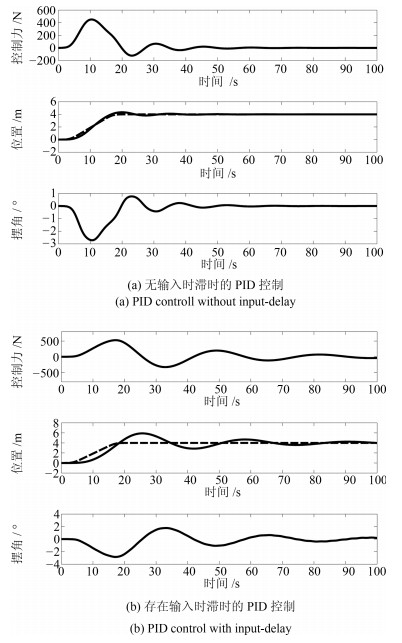
 下载:
下载: