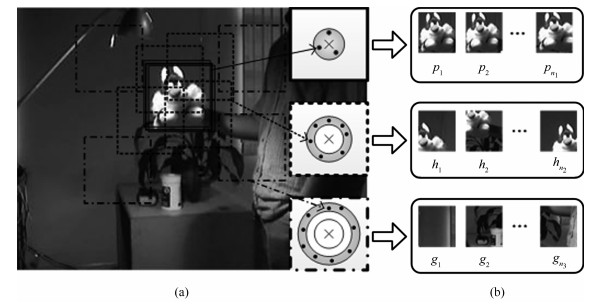
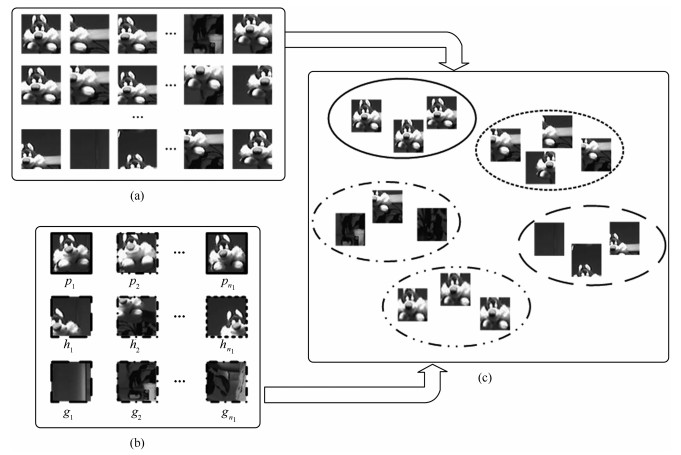
-
摘要: 本文在粒子滤波框架下提出一种基于稀疏子空间选择的两步在线跟踪方法.在跟踪的第一步,利用稀疏子空间选择算法筛选出与目标状态相似性较高的候选区域,并将目标与背景间的过渡区域定义为单独的类别以降低目标发生漂移的可能;第二步则通过构建有效的观测模型计算候选区域与目标状态间的相似性,其中相似性函数综合考虑二者在整体和局部特征上的相似性,且将目标的原始状态和当前状态都作为参考,因此增强了观测模型的可靠性;最后利用最大后验概率估计目标状态.此外,该算法通过对目标数据的更新来适应目标的表观变化.实验结果表明该算法能有效处理目标跟踪中的遮挡、运动模糊、光流与尺度变化等问题,与当前流行的9种跟踪方法在多个测试视频上的对比结果验证了该算法的有效性.Abstract: This paper proposes a two-stage online tracking method based on sparse subspace selection in the particle filter framework. At the first stage of the tracking, those candidates that highly similar to the target state are selected using the sparse subspace selection algorithm. The transition region between target and background region is defined as a separate category to alleviate the drifting. And at the second stage, a simple but effective observation model is built to calculate the similarities between the candidates and the target. The similarity measuring function not only considers the integral and local similarities comprehensively but also uses both the original target state and the state after appearance changes as references to enhance the reliability of the measurement model. Finally, the state of target is estimated according to the maximum posterior probability. Furthermore, the target appearance changes are captured by update strategy. The experimental results show that the proposed method can effectively handle the occlusion, motion blur, as well as illumination and scale changes in tracking. Comparative results on challenging benchmark image sequences show that this method performs favorable against the 9 other state-of-the-art algorithms.
-
Key words:
- Object tracking /
- appearance changes /
- sparse subspace selection /
- particle filter
-
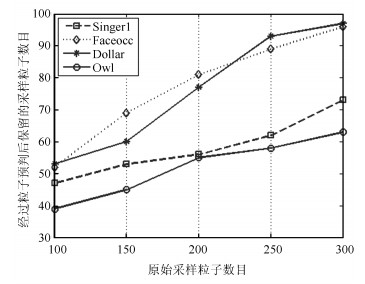
表 1 有无粒子预判处理的跟踪结果对比
Table 1 Tracking results comparing between the method with particle pre-filter and the method without particle pre-filter
平均中心位置误差(pixel) 平均面积重合参数 Singer1 Faceocc Dollar Owl Singer1 Faceocc Dollar Owl 无预判 6.6 10.2 6.4 120.1 0.67 0.80 0.83 0.06 有预判 3.6 5.1 5.5 28.8 0.85 0.93 0.85 0.47 表 2 跟踪结果的平均中心位置误差(像素)
Table 2 Average center location errors of tracking results (pixel)
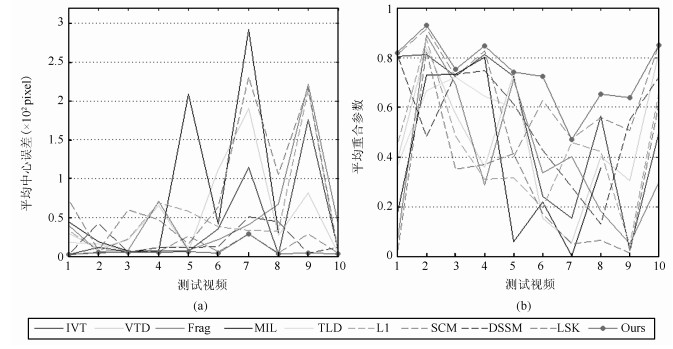
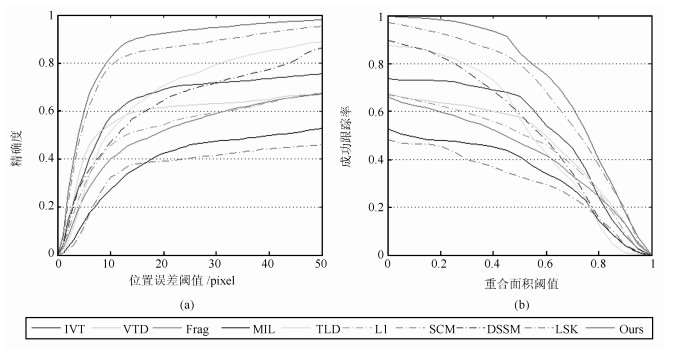
视频序列 IVT VTD Frag MIL TLD L1 SCM DSSM LSK Ours Car11 2.2 30.1 40.1 44.7 17.6 33.7 2.1 2.0 73.3 1.9 Faceocc 11.2 9.5 5.7 18.6 16.0 6.5 3.9 42.7 7.7 5.1 Sylv 6.0 21.6 7.5 7.0 5.6 22.0 5.5 5.1 59.9 5.0 Dollar 7.0 65.1 71.0 6.6 11.8 68.9 6.1 11.0 47.2 5.5 Football 6.9 6.6 7.9 209.4 13.0 58.4 26.4 11.7 15.9 6.1 Jumping 34.8 111.9 21.2 41.8 – 38.0 6.1 12.7 63.5 3.9 Owl 114.7 190.7 40.6 292.1 – 33.1 32.2 50.7 230.7 28.8 Stone 2.4 26.7 67.4 31.0 5.6 32.6 3.8 43.9 105.4 2.9 Race 176.4 82.2 221.4 – – 214.7 28.7 4.3 217.2 3.9 Singer1 9.1 3.7 42.1 241.0 27.5 5.6 3.7 11.9 7.7 3.6 表 3 跟踪结果的平均面积重合误差(像素)
Table 3 Average overlap scores of tracking results (pixel)
视频序列 IVT VTD Frag MIL TLD L1 SCM DSSM LSK Ours Car11 0.80 0.38 0.06 0.17 0.36 0.46 0.81 0.81 0.0 0.82 Faceocc 0.81 0.84 0.89 0.73 0.67 0.87 0.91 0.48 0.82 0.93 Sylv 0.72 0.57 0.69 0.73 0.72 0.48 0.72 0.73 0.35 0.75 Dollar 0.81 0.36 0.29 0.80 0.64 0.31 0.83 0.75 0.37 0.85 Football 0.72 0.73 0.71 0.06 0.60 0.32 0.40 0.61 0.41 0.74 Jumping 0.24 0.15 0.34 0.22 – 0.20 0.63 0.43 0.17 0.73 Owl 0.15 0.06 0.40 0.08 – 0.46 0.47 0.28 0.05 0.47 Stone 0.56 0.40 0.18 0.36 0.48 0.42 0.56 0.13 0.07 0.65 Race 0.02 0.30 0.05 – – 0.05 0.51 0.55 0.01 0.64 Singer1 0.50 0.82 0.30 0.32 0.35 0.66 0.85 0.72 0.62 0.85 表 4 本文跟踪算法与对比跟踪算法的平均运行时间比较
Table 4 Average running times comparing between the proposed method and other methods
跟踪方法 IVT VTD Frag MIL TLD L1 SCM DSSM LSK Ours 运行时间(s/f) 0.12 6.74 1.28 1.3 0.34 5.25 3.33 1.82 – 0.86 -
[1] Yilmaz A, Javed O, Shah M. Object tracking:a survey. ACM Computing Surveys (CSUR), 2006, 38(4):1-45 http://cn.bing.com/academic/profile?id=1995903777&encoded=0&v=paper_preview&mkt=zh-cn [2] Wu Y, Lim J, Yang M H. Online object tracking:a benchmark. In:Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA:IEEE, 2013. 2411-2418 http://cn.bing.com/academic/profile?id=2089961441&encoded=0&v=paper_preview&mkt=zh-cn [3] Smeulders A W M, Chu D M, Cucchiara R, Calderara S, Dehghan A, Shah M. Visual tracking:an experimental survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7):1442-1468 doi: 10.1109/TPAMI.2013.230 [4] Kalman R E. A new approach to linear filtering and prediction problems. Transactions of the ASME, Journal of Basic Engineering, 1960, 82:35-45 doi: 10.1115/1.3662552 [5] Doucet A, Freitas N, Gordon N. Sequential Monte Carlo Methods in Practice. New York:Springer-Verlag, 2001. http://cn.bing.com/academic/profile?id=1483307070&encoded=0&v=paper_preview&mkt=zh-cn [6] Mei X, Ling H B. Robust visual tracking using L1 minimization. In:Proceedings of the 2009 International Conference on Computer Vision. Kyoto, Japan:IEEE, 2009. 1436-1443 [7] Zhang T Z, Ghanem B, Liu S, Ahuja N. Robust visual tracking via multi-task sparse learning. In:Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA:IEEE, 2012. 2042-2049 http://cn.bing.com/academic/profile?id=2158917775&encoded=0&v=paper_preview&mkt=zh-cn [8] Hong Z B, Mei X, Prokhorov D, Tao D C. Tracking via robust multi-task multi-view joint sparse representation. In:Proceedings of the 2013 International Conference on Computer Vision. Sydney, NSW:IEEE, 2013. 649-656 http://cn.bing.com/academic/profile?id=2098711149&encoded=0&v=paper_preview&mkt=zh-cn [9] Zhang S P, Yao H X, Zhou H Y, Sun X, Liu S H. Robust visual tracking based on online learning sparse representation. Neurocomputing, 2013, 100:31-40 doi: 10.1016/j.neucom.2011.11.031 [10] Adam A, Rivlin E, Shimshoni I. Robust fragments-based tracking using the integral histogram. In:Proceedings of the 2006 IEEE Conference on Computer Vision and Pattern Recognition. New York, USA:IEEE, 2006. 798-805 http://cn.bing.com/academic/profile?id=2121193292&encoded=0&v=paper_preview&mkt=zh-cn [11] He S F, Yang Q X, Lau R W H, Wang J, Yang M H. Visual tracking via locality sensitive histograms. In:Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA:IEEE, 2013. 2427-2434 http://cn.bing.com/academic/profile?id=2108215708&encoded=0&v=paper_preview&mkt=zh-cn [12] Ross D A, Lim J, Lin R S, Yang M-H. Incremental learning for robust visual tracking. International Journal of Computer Vision, 2008, 77(1):125-141 http://cn.bing.com/academic/profile?id=2139047213&encoded=0&v=paper_preview&mkt=zh-cn [13] Kwon J, Lee K M. Visual tracking decomposition. In:Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA:IEEE, 2010. 1269-1276 http://cn.bing.com/academic/profile?id=2098854771&encoded=0&v=paper_preview&mkt=zh-cn [14] Liu B Y, Huang J Z, Yang L, Kulikowsk C. Robust tracking using local sparse appearance model and k-selection. In:Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA:IEEE, 2011. 1313-1320 http://cn.bing.com/academic/profile?id=2066513304&encoded=0&v=paper_preview&mkt=zh-cn [15] Yang F, Lu H C, Yang M H. Robust superpixel tracking. IEEE Transactions on Image Processing, 2014, 23(4):1639-1651 doi: 10.1109/TIP.2014.2300823 [16] Babenko B, Yang M H, Belongie S. Visual tracking with online multiple instance learning. In:Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami FL, USA:IEEE, 2009. 983-990 http://cn.bing.com/academic/profile?id=2167089254&encoded=0&v=paper_preview&mkt=zh-cn [17] Kalal Z, Matas J, Mikolajczyk K. P-N learning:bootstrapping binary classifiers by structural constraints. In:Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA:IEEE, 2010. 49-56 http://cn.bing.com/academic/profile?id=2147533695&encoded=0&v=paper_preview&mkt=zh-cn [18] Xie Y, Zhang W S, Li C H, Lin S Y, Qu Y Y, Zhang Y H. Discriminative object tracking via sparse representation and online dictionary learning. IEEE Transactions on Cybernetics, 2014, 44(4):539-553 doi: 10.1109/TCYB.2013.2259230 [19] Zhuang B H, Lu H C, Xiao Z Y, Wang D. Visual tracking via discriminative sparse similarity map. IEEE Transactions on Image Processing, 2014, 23(4):1872-1881 doi: 10.1109/TIP.2014.2308414 [20] Zhong W, Lu H C, Yang M H. Robust object tracking via sparsity-based collaborative model. In:Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA:IEEE, 2012. 1838-1845 http://cn.bing.com/academic/profile?id=2016075127&encoded=0&v=paper_preview&mkt=zh-cn [21] Elhamifar E, Sapiro G, Sastry S. Dissimilarity-based sparse subset selection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014. DOI: 10.1109/TPAMI.2015.2511748 [22] Elhamifar E, Vidal R. Sparse subspace clustering:algorithm, theory, and application. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11):2765-2781 doi: 10.1109/TPAMI.2013.57 [23] Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2010, 3(1):1-122 doi: 10.1561/2200000016 -





 下载:
下载: