面向电力系统快速频率响应的数据与模型驱动预测控制

吴卓睿; 张萌; 管晓宏

doi:10.16383/j.aas.c250261

面向电力系统快速频率响应的数据与模型驱动预测控制

doi: 10.16383/j.aas.c250261 cstr: 32138.14.j.aas.c250261

1.
西安交通大学网络空间安全学院西安 710049

基金项目: 国家自然科学基金(62033005, 62273270), 能源陕西实验室项目(ESLB202413)资助

详细信息

作者简介:
吴卓睿：西安交通大学网络空间安全学院博士研究生. 2021年获得西安交通大学学士学位. 主要研究方向为数据驱动电力系统控制. E-mail: wzr445576941@stu.xjtu.edu.cn

张萌：西安交通大学网络空间安全学院教授. 2018年获得浙江大学博士学位. 主要研究方向为电力系统控制、优化与安全. 本文通信作者. E-mail: mengzhang2009@xjtu.edu.cn

管晓宏：中国科学院院士, 西安交通大学电子与信息学部教授. 1993年获得美国康涅狄格大学博士学位. 主要从事能源电力系统优化与安全理论及应用研究. E-mail: xhguan@mail.xjtu.edu.cn

计量
- 文章访问数: 24
- HTML全文浏览量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2025-06-16
- 录用日期: 2025-08-19
- 网络出版日期: 2025-09-08

Data and Model-driven Predictive Control for Fast Frequency Response in Power Systems

1.
School of Cyber Sicence and Engineering, Xi＇an Jiaotong University, Xi＇an 710049

Funds: Supported by National Natural Science Foundation of China (62033005, 62273270), and S&T Program of Energy Shaanxi Laboratory (ESLB202413)

More Information

Author Bio:
WU Zhuo-Rui　Ph.D. candidate at the School of Cyber Sicence and Engineering, Xi′an Jiaotong University. He received his bachelor degree from Xi′an Jiaotong University in 2012. His main research interest is data-driven power system control

ZHANG Meng　Professor at the School of Cyber Sicence and Engineering, Xi＇an Jiaotong University. He received his Ph.D. degree from Zhejiang University in 2018. His research interest covers control, optimization and security of power sytems. Corresponding author of this paper

GUAN Xiao-Hong　Member of the Chinese Academy of Sciences, professor at the Faculty of Electronic and Information Engineering, Xi′an Jiaotong University. He received his Ph.D. degree from the University of Connecticut in 1993. His research interest covers energy and power system optimization and security theory and application research

摘要

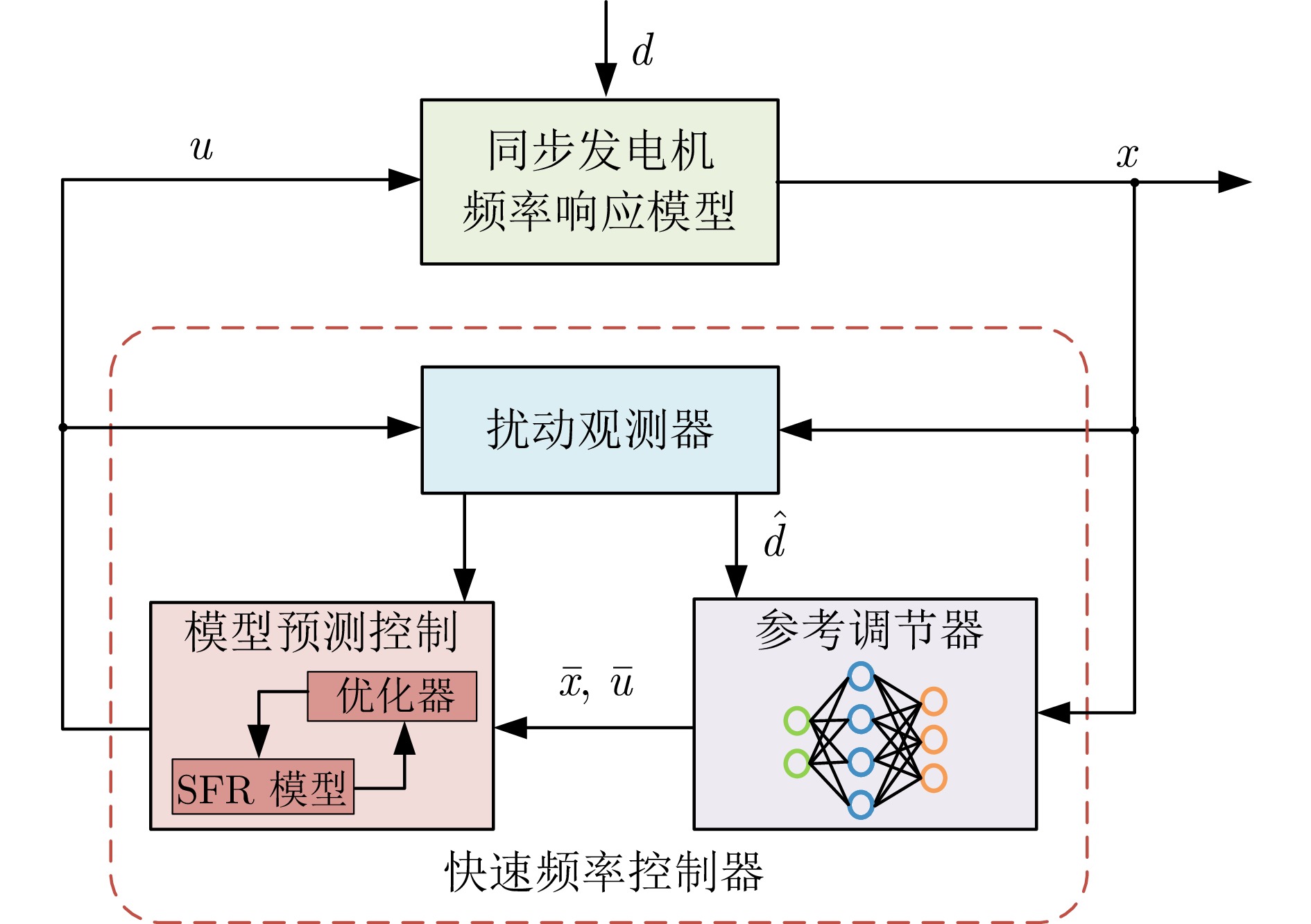
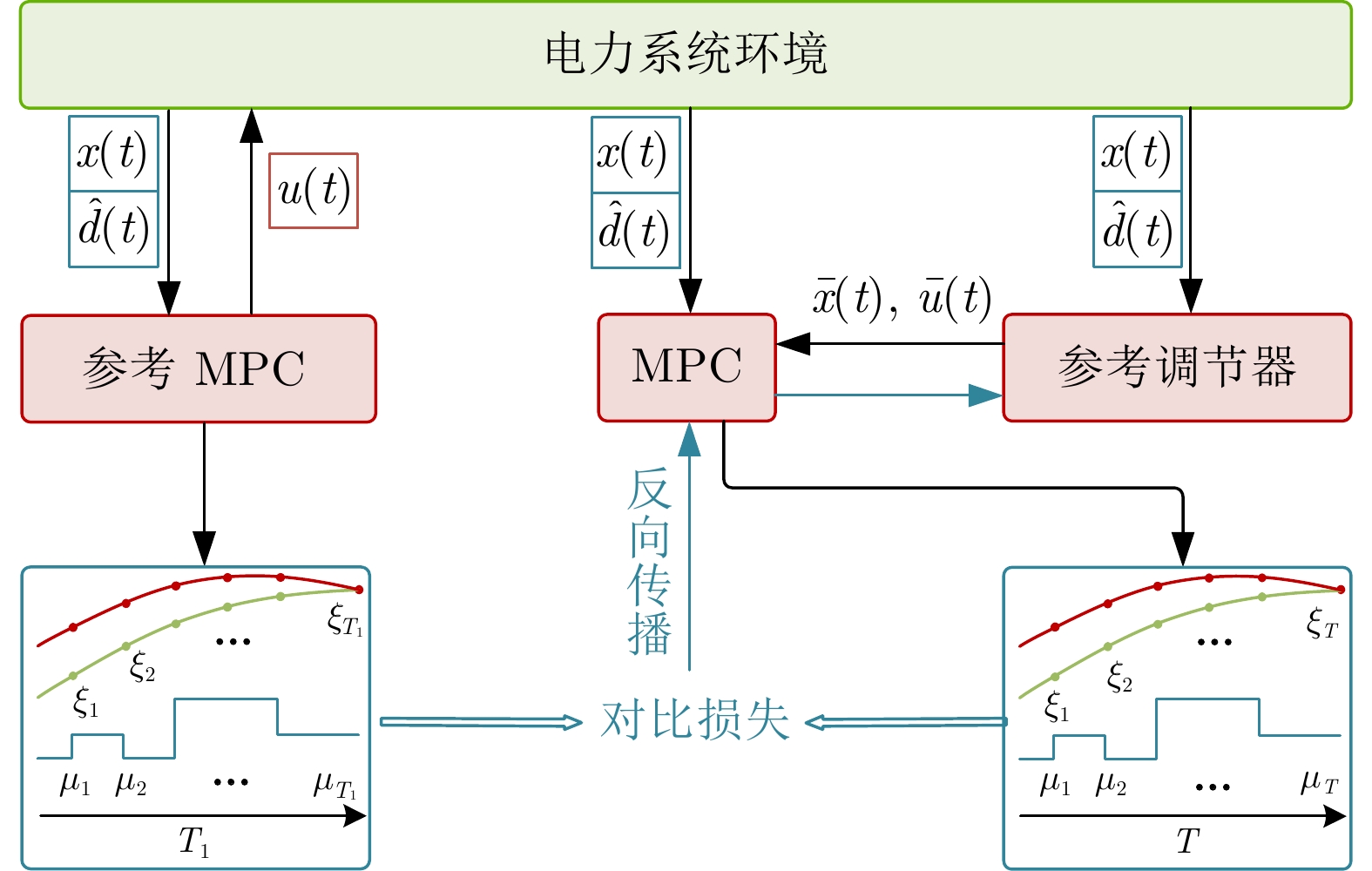
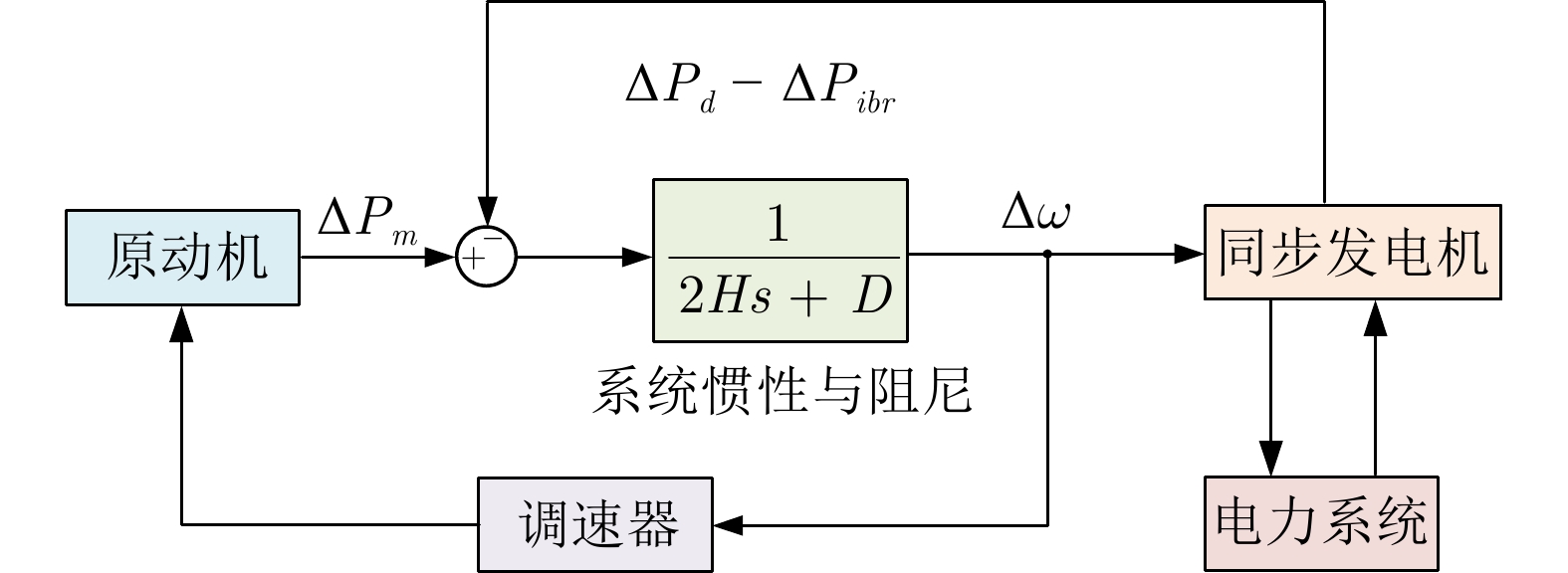
摘要: 维持频率稳定是电力系统控制的一个重要目标. 然而, 高渗透率新能源可能导致频繁的功率波动, 对系统频率调节造成不利影响. 为解决这一问题, 通常需要快速调节变流器资源的功率输出, 响应系统频率波动以实现快速频率控制. 针对电力系统快速频率控制, 提出一种数据与模型驱动的预测控制方法. 首先, 设计数据驱动的扰动观测器以估计负荷变化与新能源波动等系统扰动. 为优化控制性能, 利用基于神经网络设计的参考调节器为模型预测控制器提供虚拟参考. 通过学习长预测时域模型预测控制器, 参考调节器能够提升短预测时域控制器性能, 因而降低了所需的计算时间. 最终, 仿真对比结果表明所提方法能够有效提高频率控制性能.
- 快速频率控制 /
- 变流器资源 /
- 模型预测控制 /
- 参考调节器 /
- 深度学习
Abstract: A key objective of power system control is to maintain frequency stability. However, high penetration of renewable energy resources may cause frequent power fluctuations, resulting in negative impact on system frequency regulation. To deal with this issue, it commonly requires to rapidly adjust the power output of inverter-based resources in response to system frequency fluctations, achieving fast frequency control. This paper proposes a data and model-driven predictive control method for fast frequency control in power systems. First, a data-driven disturbance observer is designed to estimate system disturbance such as load changes, renewable energy fluctuations and so on. To optimize the control performance, the reference governor designed by a neural network provides virtual reference for the model predictive controller. The reference governor enhances the performance of the controller with a short prediction horizon through learning a long prediction horizon controller, thus reducing the required computation time. Finally, simulation comparison results demonstrate that the proposed method can effectively improve the frequency control performance.
- Fast frequency control /
- inverter-based resource /
- model predictive control /
- reference governor /
- deep learning

HTML全文

图 1 系统频率响应模型

Fig. 1 System frequency response model

下载: 全尺寸图片幻灯片

图 2 快速频率控制框图

Fig. 2 Block diagram of fast frequency control

下载: 全尺寸图片幻灯片

图 3 不同预测时域下系统频率稳态误差

Fig. 3 Steady-state error of the system frequency under different prediction horizons

下载: 全尺寸图片幻灯片

图 4 基于深度学习的参考调节器方法框架

Fig. 4 The framwork of the deep learning-based reference governor

下载: 全尺寸图片幻灯片

图 5 IEEE 39母线测试系统

Fig. 5 IEEE 39 bus test system

下载: 全尺寸图片幻灯片

图 6 参考调节器训练结果

Fig. 6 Training results of the reference governors

下载: 全尺寸图片幻灯片

图 7 负荷阶跃扰动下频率动态

Fig. 7 Frequency dynamics under the step load disturbance

下载: 全尺寸图片幻灯片

图 8 负荷阶跃扰动下IBR有功输出

Fig. 8 Active output of IBR under step load disturbance

下载: 全尺寸图片幻灯片

图 9 负荷阶跃扰动下参考调节器输出的虚拟参考

Fig. 9 Virtual references obtained from reference governors under step load disturbance

下载: 全尺寸图片幻灯片

图 10 输出功率限制下的频率动态与有功输出

Fig. 10 Frequency dynamics and active power output under limited power output

下载: 全尺寸图片幻灯片

图 11 风力发电功率变化

Fig. 11 Change of wind power

下载: 全尺寸图片幻灯片

图 12 风力发电波动下的频率动态

Fig. 12 Frequency dynamics under wind power fluctations

下载: 全尺寸图片幻灯片

图 13 风力发电波动下的IBR有功输出

Fig. 13 Active output of IBR under wind power fluctations

下载: 全尺寸图片幻灯片

图 14 线路跳闸下的频率动态

Fig. 14 Frequency dynamics under line tripping

下载: 全尺寸图片幻灯片

图 15 线路跳闸下的IBR有功输出

Fig. 15 Active output of IBR under line tripping

下载: 全尺寸图片幻灯片

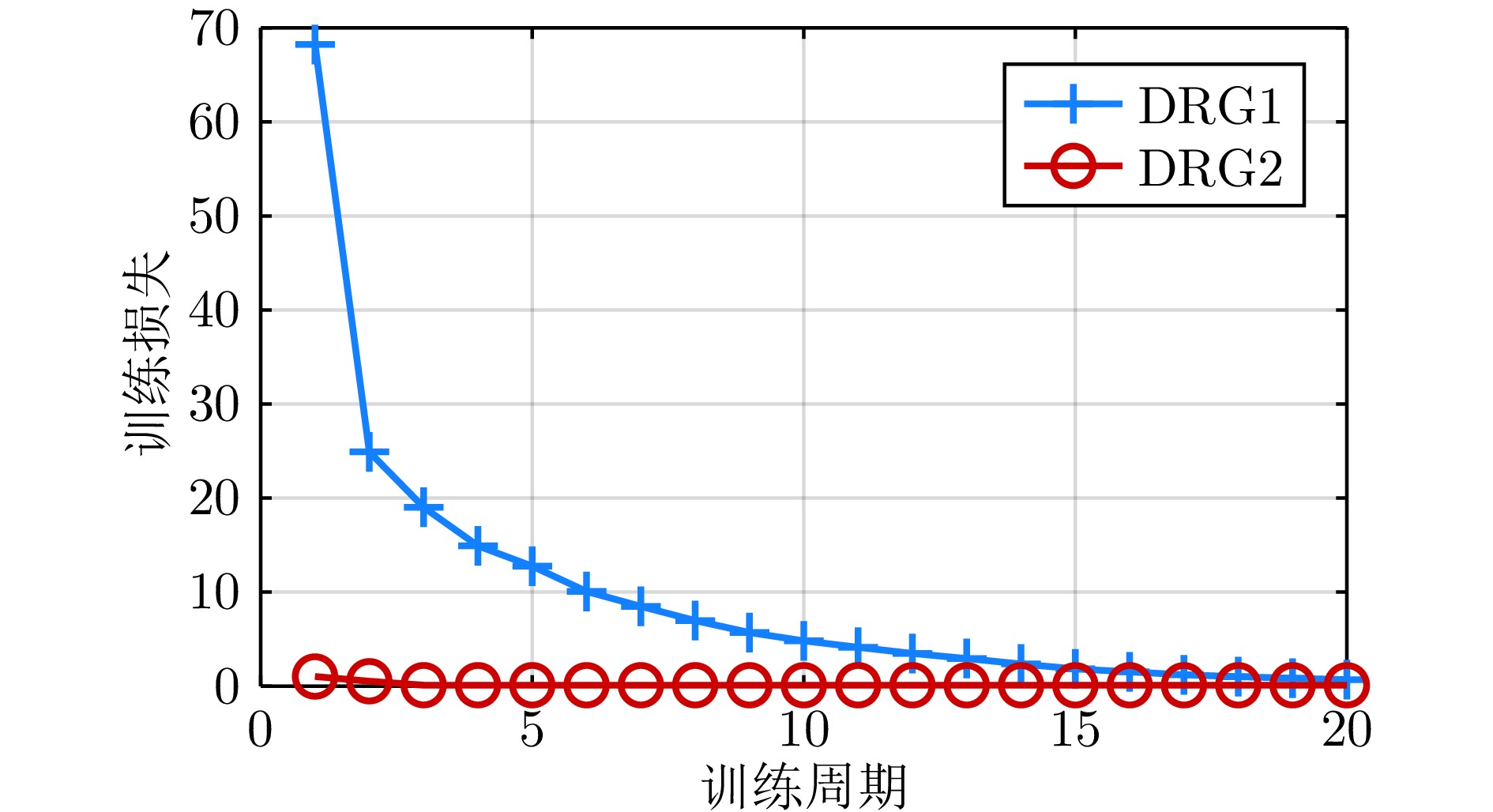
表 1 不同预测时域下参考调节器训练误差

Table 1 Training error of the reference governor with different prediction horizons

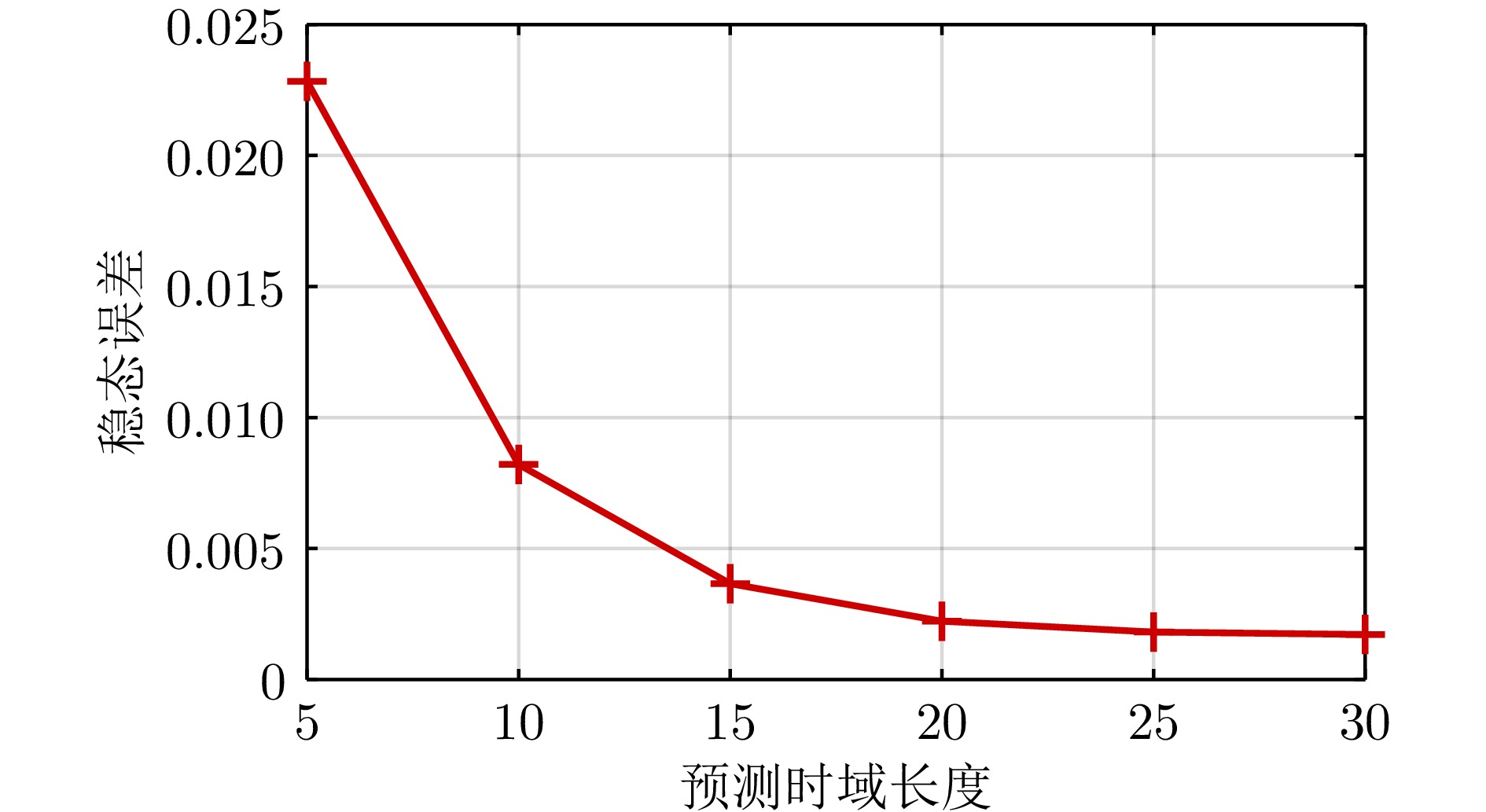
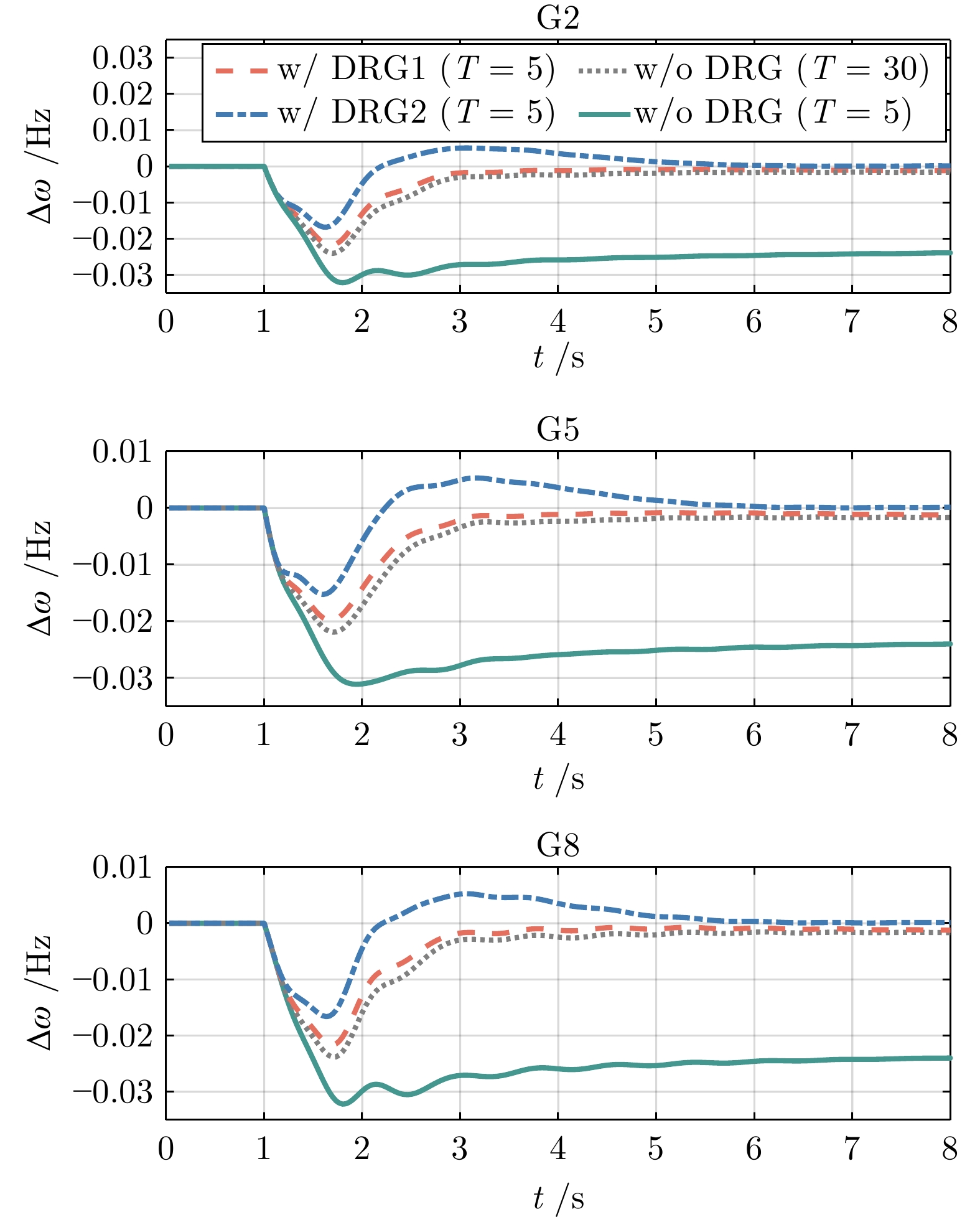
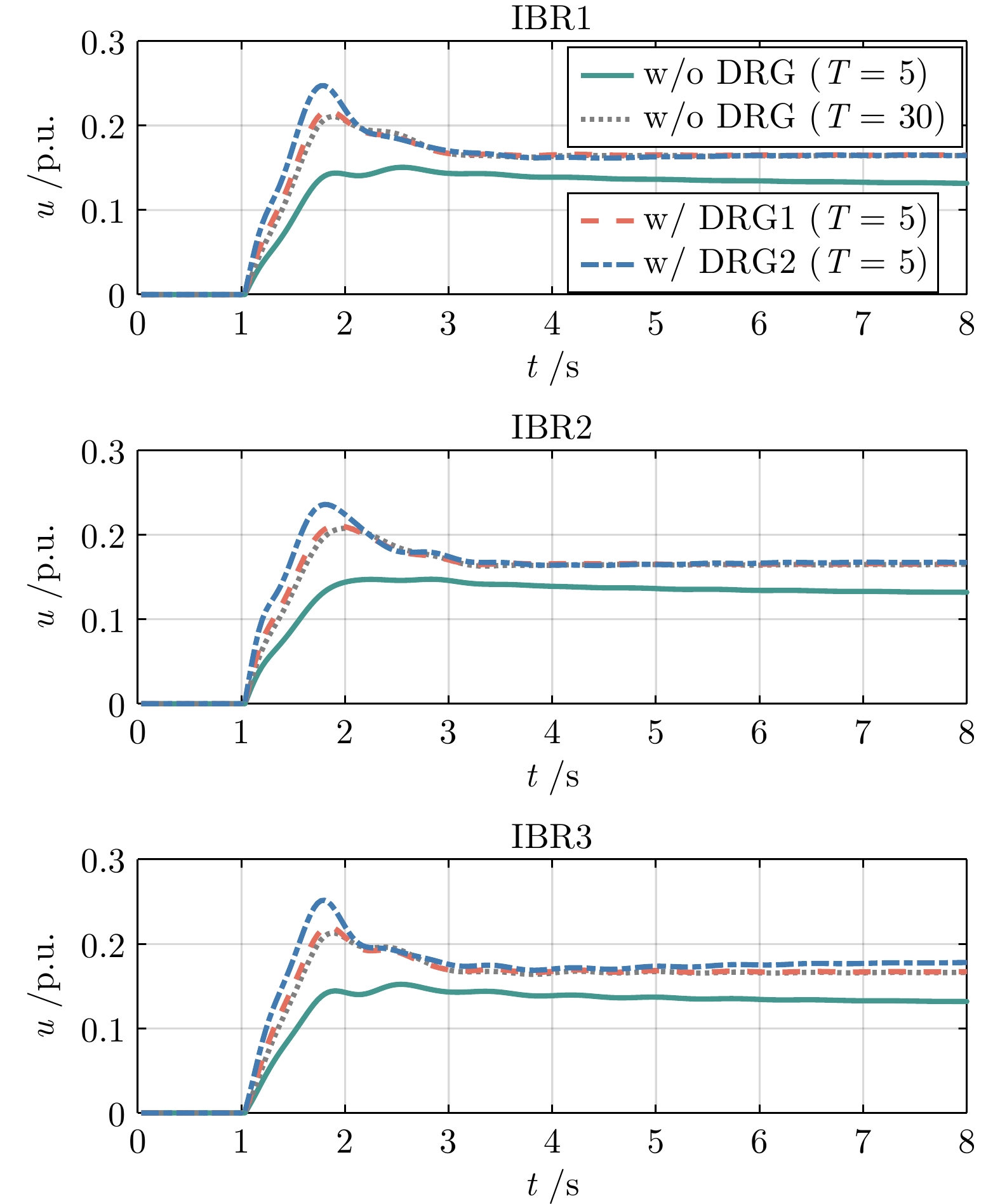
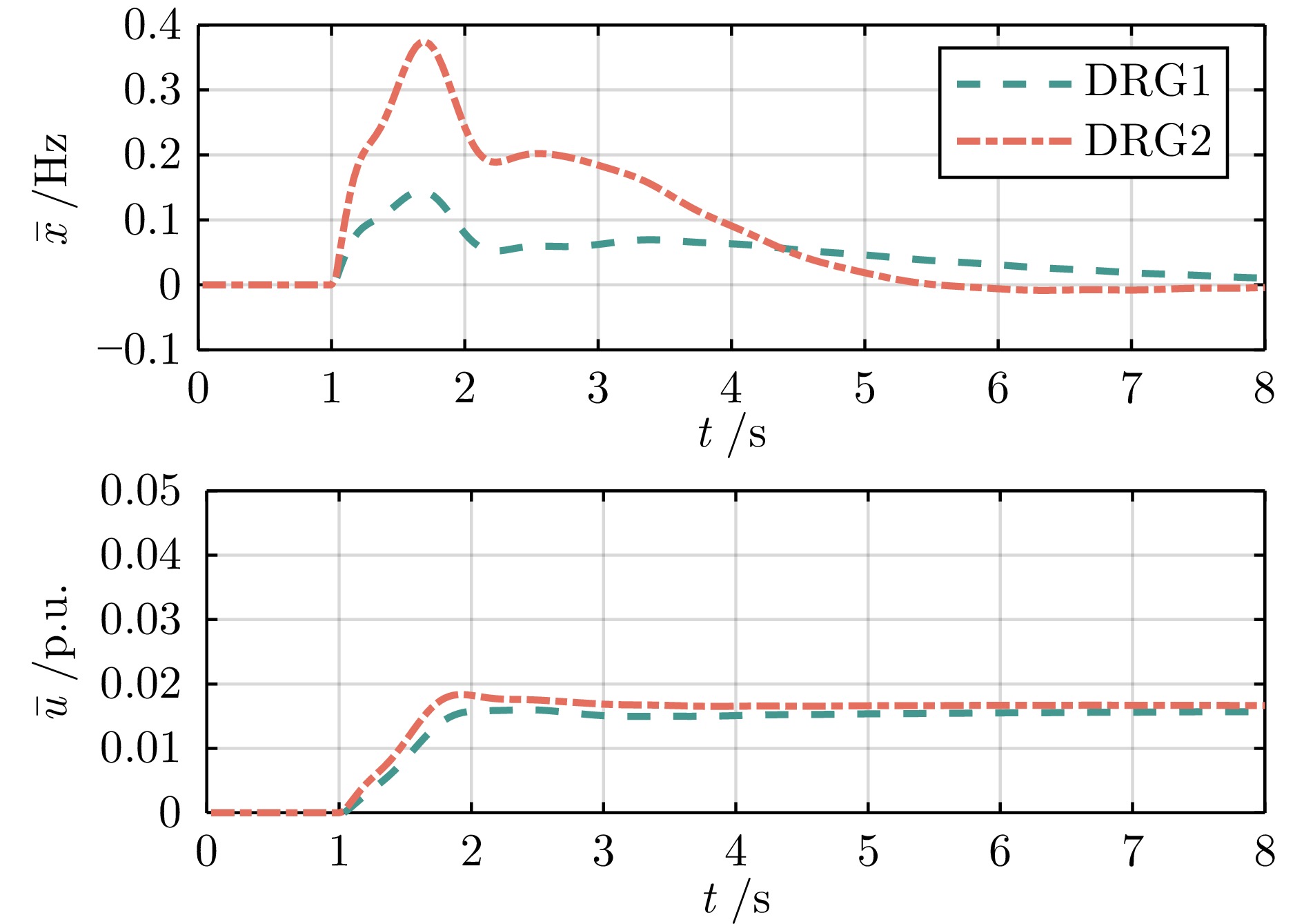
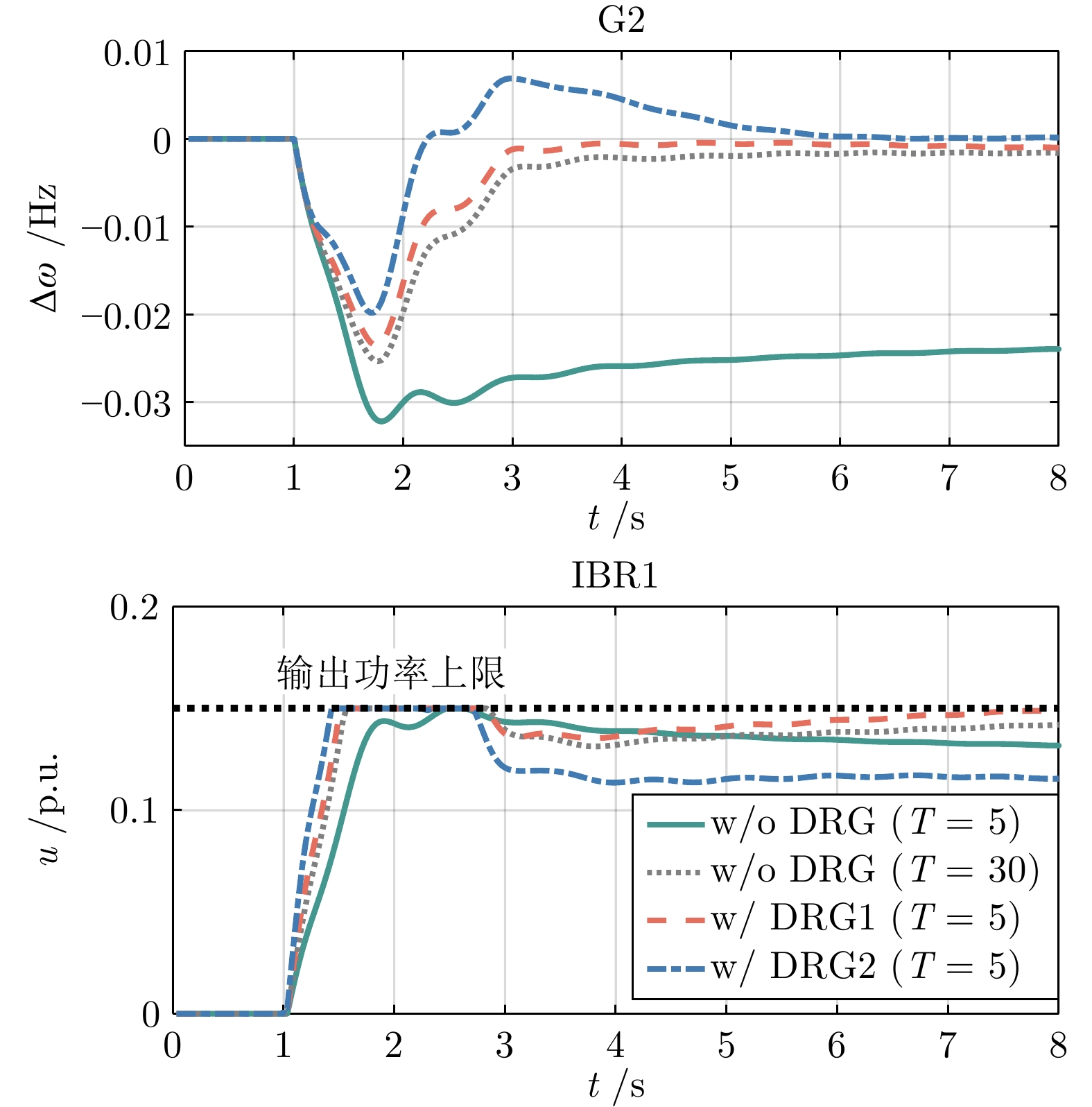
预测时域	$ T = 2 $	$ T = 3 $	$ T = 5 $	$ T = 10 $
训练误差	447	4.14	0.686	0.130

下载: 导出CSV

表 2 负荷阶跃扰动下四种控制器性能指标对比

Table 2 Comparison of performance metrics of the four controllers under step load disturbance

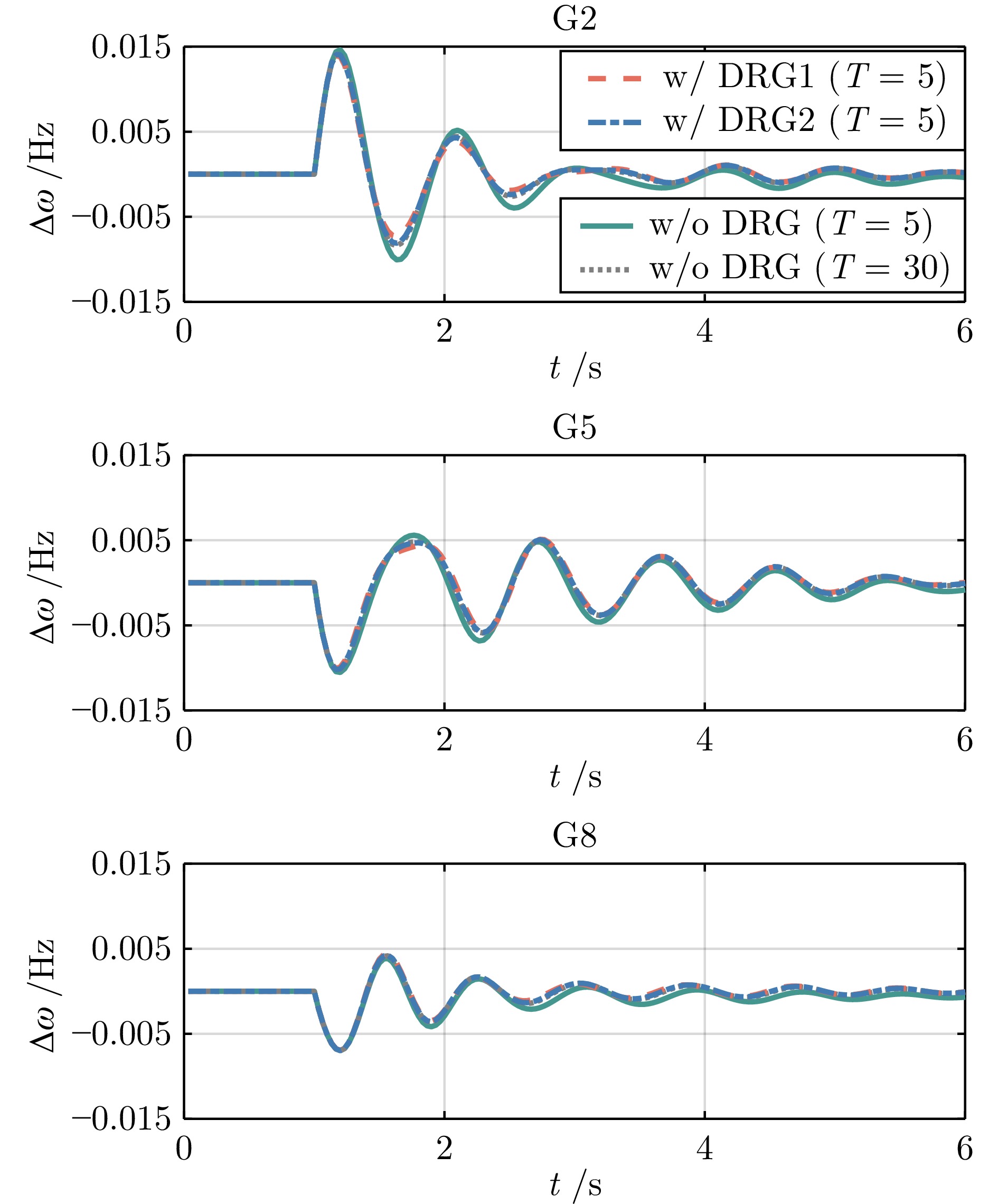
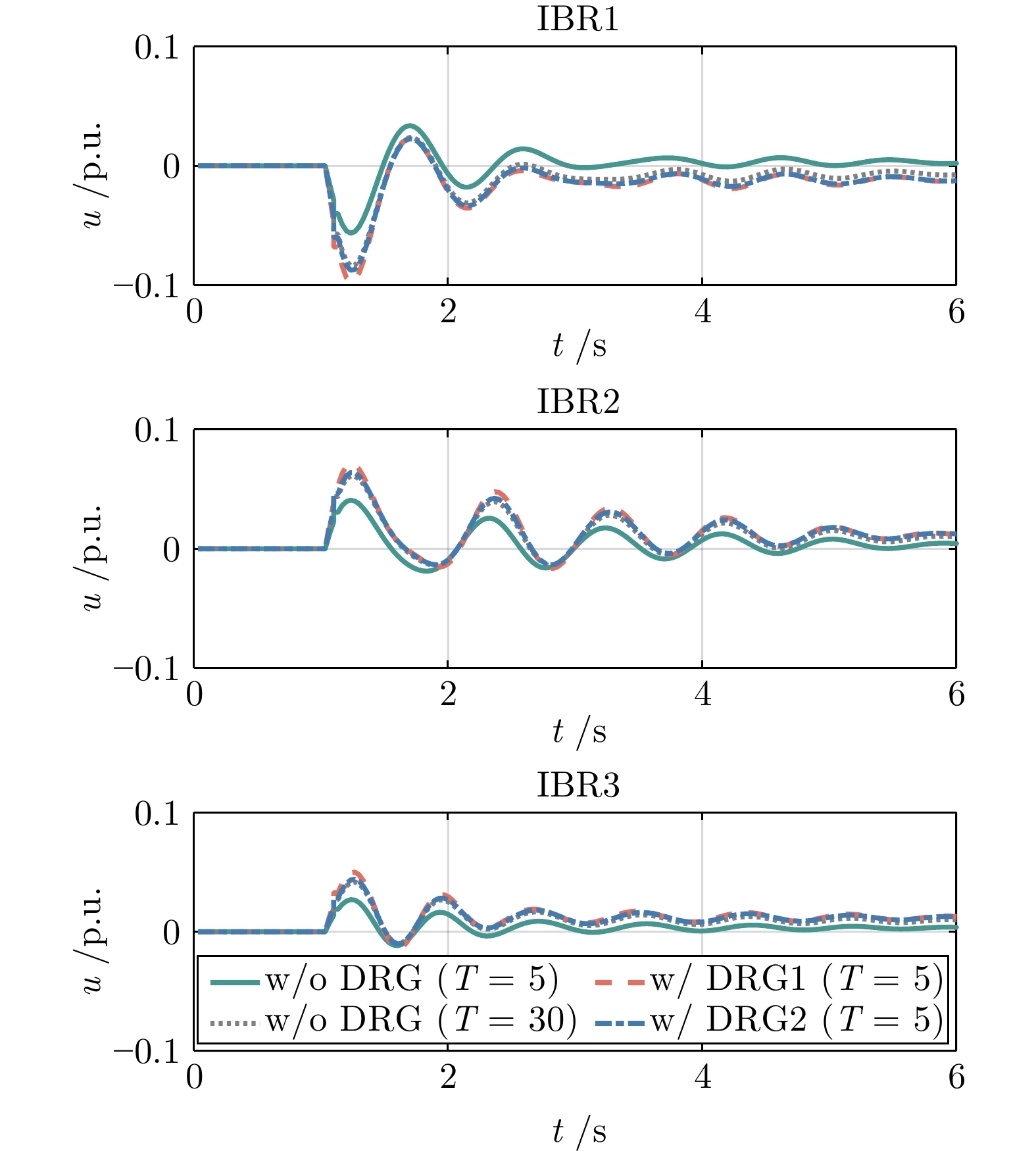
控制器	最大频率偏差/Hz	稳态频率偏差/Hz	计算时间/ms
w/o DRG ($ T = 5 $)	0.0322	0.0232	0.91
w/o DRG ($ T = 30 $)	0.0241	0.0017	5.26
w/ DRG1 ($ T = 5 $)	0.0218	0.0016	1.12
w/ DRG ($ T = 5 $)	0.0168	0.0002	1.05

下载: 导出CSV

表 3 风力发电波动下四种控制器性能指标对比

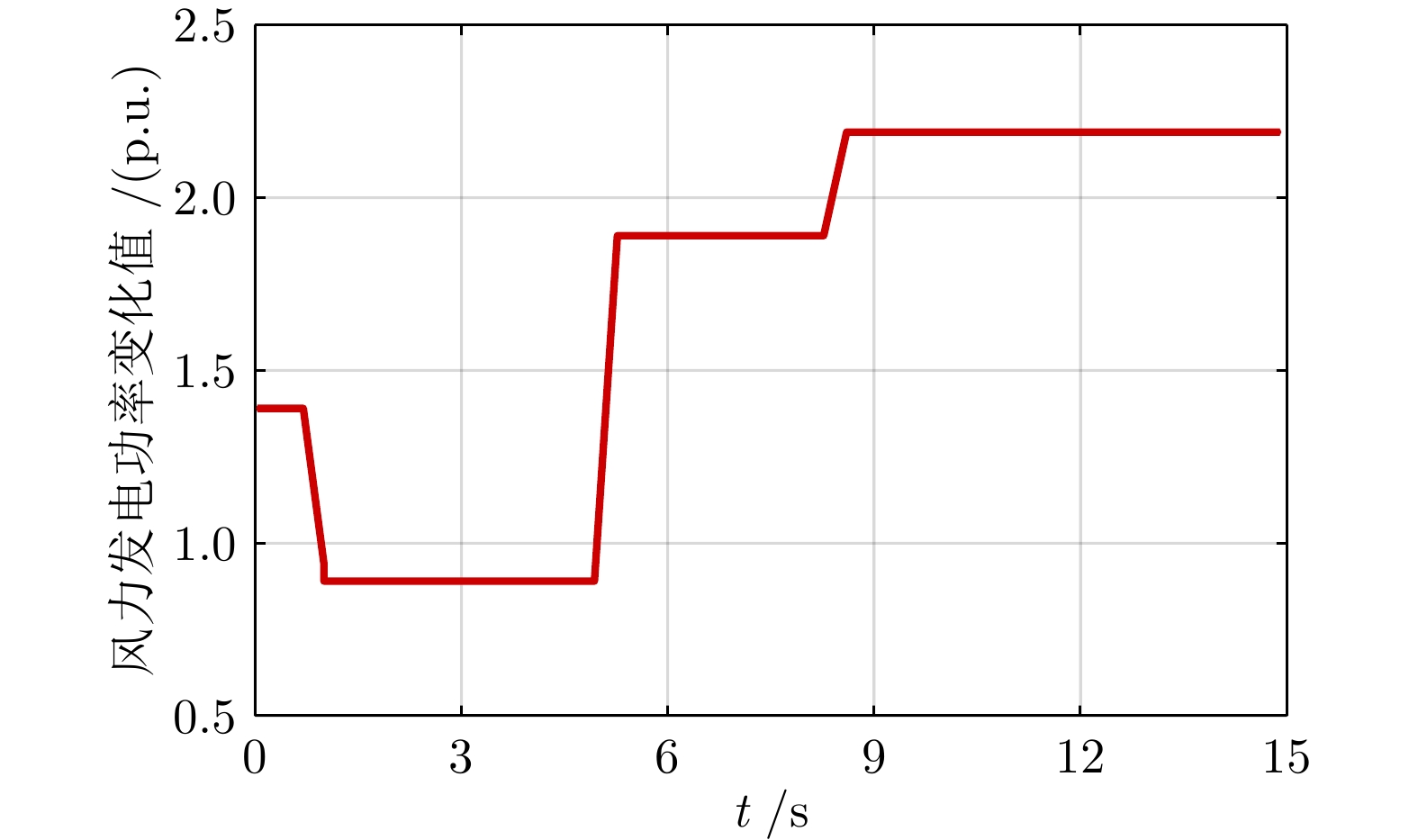
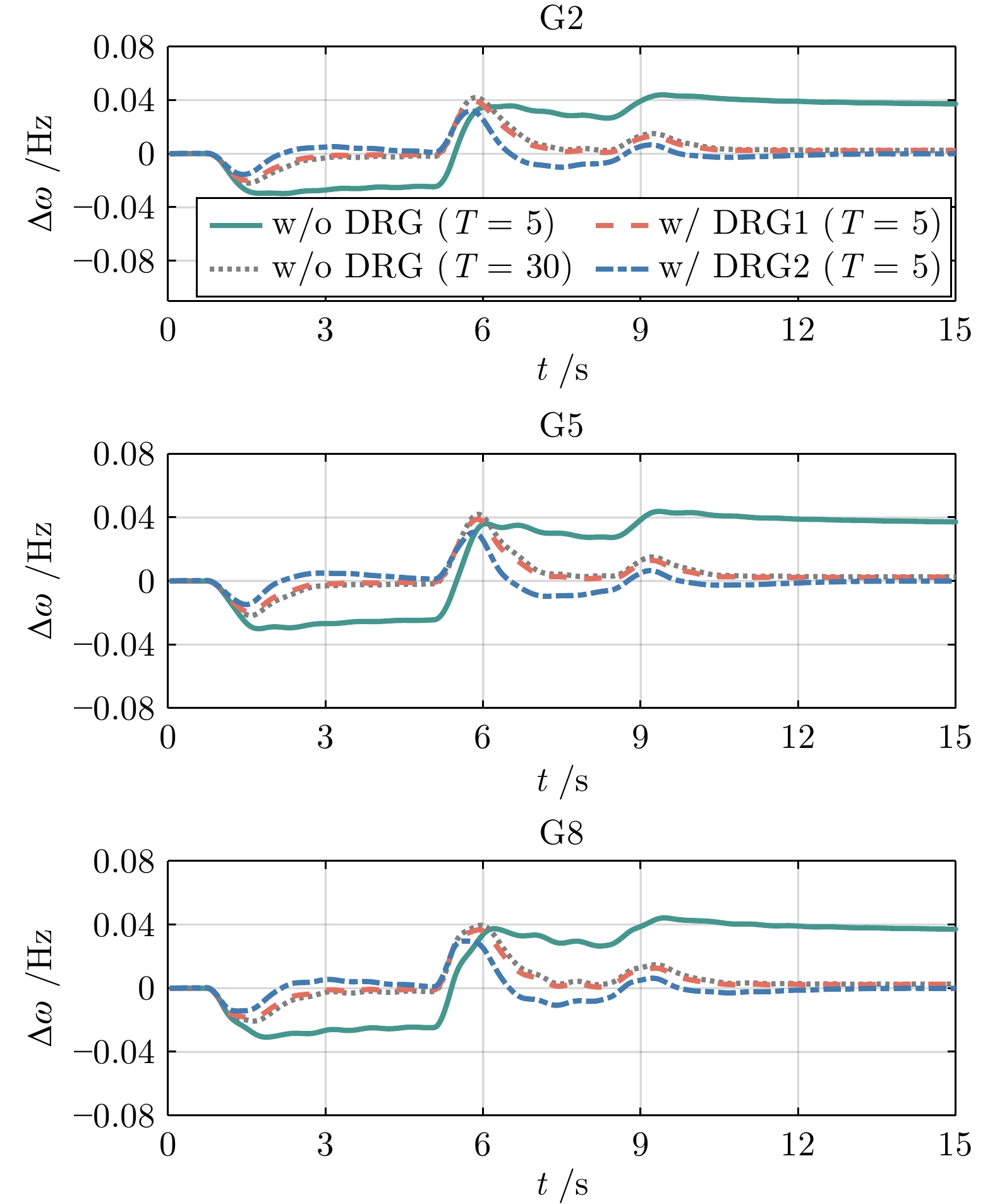
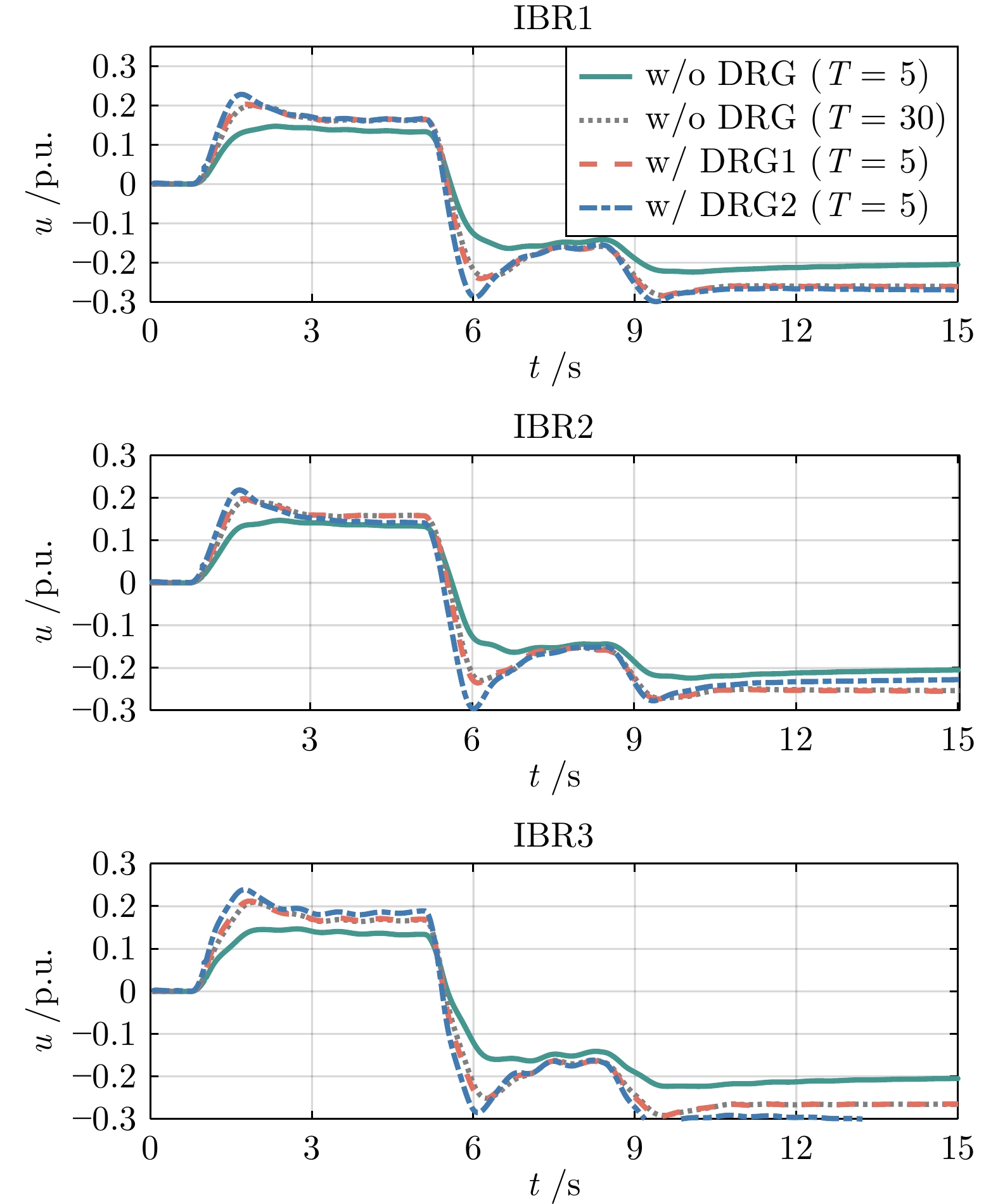
Table 3 Comparison of performance metrics of the four controllers under wind power fluctations

控制器	最大频率偏差/Hz	稳态频率偏差/Hz	计算时间/ms
w/o DRG ($ T=5 $)	0.0442	0.0372	0.91
w/o DRG ($ T=30 $)	0.0419	0.0026	5.17
w/ DRG1 ($ T=5 $)	0.0392	0.0025	1.00
w/ DRG2 ($ T=5 $)	0.0320	0.0001	1.08

下载: 导出CSV

参考文献(36)

[1]	舒印彪, 陈国平, 贺静波, 张放. 构建以新能源为主体的新型电力系统框架研究. 中国工程科学, 2021, 23(6): 61−69 doi: 10.15302/J-SSCAE-2021.06.003 Shu Yin-Biao, Chen Guo-Ping, He Jing-Bo, Zhang Fang. Building a new electric power system based on new energy sources. Strategic Study of CAE, 2021, 23(6): 61−69 doi: 10.15302/J-SSCAE-2021.06.003
[2]	周孝信, 赵强, 张玉琼, 杨宏华. “双碳”目标下我国能源电力系统发展趋势分析: 绿电替代与绿氢替代. 中国电机工程学报, 2024, 44(17): 6707−6721 Zhou Xiao-Xin, Zhao Qiang, Zhang Yu-Qiong, Yang Hong-Hua. Analysis of the development trend of China's energy and power system under the dual carbon target: Green electricity substitution and green hydrogen substitution. Proceedings of the CSEE, 2024, 44(17): 6707−6721
[3]	马士全, 丁进良. 面向可再生能源消纳的火电机组控制结构综合与分析. 自动化学报, 2024, 50(5): 1−15 Ma Shi-Quan, Ding Jin-Liang. Syntheses and analyses of control structure for coal-fired power plants oriented to renewable energy accommodation. Acta Automatica Sinica, 2024, 50(5): 1−15
[4]	张文亮, 汤广福, 查鲲鹏, 贺之渊. 先进电力电子技术在智能电网中的应用. 中国电机工程学报, 2010, 30(4): 1−7 Zhang Wen-Liang, Yang Guang-Fu, Cha Kun-Peng, He Zhi-Yuan. Application of advanced power electronics in smart grid. Proceedings of CSEE, 2010, 30(4): 1−7
[5]	Dvorkin Y, Lubin M, Backhaus S, Chertkov M. Uncertainty sets for wind power generation. IEEE Transactions on Power Systems, 2015, 31(4): 3326−3327
[6]	Li C, Yang Y, Cao Y, Aleshina A, Xu J, Blaabjerg F. Grid inertia and damping support enabled by proposed virtual inductance control for grid-forming virtual synchronous generator. IEEE Transactions on Power Electronics, 2022, 38(1): 294−303
[7]	Tang Y, Dvijotham K, Low S. Real-time optimal power flow. IEEE Transactions on Smart Grid, 2017, 8(6): 2963−2973 doi: 10.1109/TSG.2017.2704922
[8]	Yan Z, Xu Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Transactions on Power Systems, 2020, 35(6): 4599−4608 doi: 10.1109/TPWRS.2020.2999890
[9]	Cui W, Jiang Y, Zhang B. Reinforcement learning for optimal primary frequency control: A lyapunov approach. IEEE Transactions on Power Systems, 2022, 38(2): 1676−1688
[10]	Fan B, Wang X. A lyapunov-based nonlinear power control algorithm for grid-connected vscs. IEEE Transactions on Industrial Electronics, 2021, 69(3): 2916−2926
[11]	Dreidy M, Mokhlis H, Mekhilef S. Inertia response and frequency control techniques for renewable energy sources: A review. Renewable and Sustainable Energy Reviews, 2017, 69: 144−155 doi: 10.1016/j.rser.2016.11.170
[12]	Liu J, Liu X, Liu J, Li X, Wang J. Adaptive-droop-coefficient VSG control for cost-efficient grid frequency support. IEEE Transactions on Power Systems, 2024, 39(5): 6768−6771 doi: 10.1109/TPWRS.2024.3424149
[13]	Reißner F, de Carne G. Virtual synchronous machine integration on a commercial flywheel for frequency grid support. IEEE Transactions on Power Electronics, 2024, 39(10): 12086−12090 doi: 10.1109/TPEL.2024.3369980
[14]	Baros S, Chen Y. C, Dhople S. V. Examining the economic optimality of automatic generation control. IEEE Transactions on Power Systems, 2021, 36(5): 4611−4620 doi: 10.1109/TPWRS.2021.3067445
[15]	Venkat A N, Hiskens I A, Rawlings J B, Wright S J. Distributed MPC strategies with application to power system automatic generation control. IEEE Transactions on Control Systems Technology, 2008, 16(6): 1192−1206 doi: 10.1109/TCST.2008.919414
[16]	Shiroei M, Ranjbar A. Supervisory predictive control of power system load frequency control. International Journal of Electrical Power & Energy Systems, 2014, 61: 70−80
[17]	Ekomwenrenren E, Simpson-Porco J W, Farantatos E, Patel M, Haddadi A, Zhu L. Data-driven fast frequency control using inverter-based resources. IEEE Transactions on Power Systems, 2023, 39(4): 5755−5768
[18]	Mavalizadeh H, Espinosa L A D, Almassalkhi M R. Decentralized frequency control using packet-based energy coordination. In: Proceedings of 2020 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm). New York, USA: IEEE, 2020. 1–7
[19]	席裕庚, 李德伟, 林姝. 模型预测控制—现状与挑战. 自动化学报, 2013, 39(3): 222−236 doi: 10.1016/S1874-1029(13)60024-5 Xi Yu-Geng, Li De-Wei, Lin Shu. Model predictive control — Status and challenges. ACTA Automatica Sinica, 2013, 39(3): 222−236 doi: 10.1016/S1874-1029(13)60024-5
[20]	Fuchs A, Imhof M, Demiray T, Morari M. Stabilization of large power systems using VSC–HVDC model predictive control. IEEE Transactions on Power Delivery, 2013, 29(1): 480−488
[21]	Papangelis L, Debry M S, Prevost T, Panciatici P, Van Cutsem T. Decentralized model predictive control of voltage source converters for ac frequency containment. International Journal of Electrical Power & Energy Systems, 2018, 98: 342−349
[22]	Stanojev O, Markovic U, Aristidou P, Hug G, Callaway D, Vrettos E. MPC-based fast frequency control of voltage source converters in low-inertia power systems. IEEE Transactions on Power Systems, 2020, 37(4): 3209−3220
[23]	Zholbaryssov M, Dominguez-Garcia A. D. Safe data-driven secondary control of distributed energy resources. IEEE Transactions on Power Systems, 2021, 36(6): 5933−5943 doi: 10.1109/TPWRS.2021.3084440
[24]	Leung J, Permenter F, Kolmanovsky I V. A stability governor for constrained linear-quadratic MPC without terminal constraints. Automatica, 2024, 164: Article No. 111650 doi: 10.1016/j.automatica.2024.111650
[25]	Leung J, Permenter F, Kolmanovsky I V. A computational governor for maintaining feasibility low computational cost in model predictive control. IEEE Transactions on Automatic Control, 2023, 69(5): 2791−2806
[26]	Limón D, Alamo T, Salas F, Camacho E F. On the stability of constrained MPC without terminal constraint. IEEE Transactions on Automatic Control, 2006, 51(5): 832−836 doi: 10.1109/TAC.2006.875014
[27]	Anderson P M, Mirheydar M. A low-order system frequency response model. IEEE Transactions on Power Systems, 2002, 5(3): 720−729
[28]	Ekomwenrenren E, Tang Z, Simpson-Porco J W, Farantatos E, Patel M, Hooshyar H. Hierarchical coordinated fast frequency control using inverter-based resources. IEEE Transactions on Power Systems, 2021, 36(6): 4992−5005 doi: 10.1109/TPWRS.2021.3075641
[29]	Willems J C, Rapisarda P, Markovsky I, de Moor B L. A note on persistency of excitation. Systems & Control Letters, 2005, 54(4): 325−329
[30]	de Persis C, Tesi P. Formulas for data-driven control: Stabilization, optimality, and robustness. IEEE Transactions on Automatic Control, 2019, 65(3): 909−924
[31]	Amos B, Jimenez I, Sacks J, Boots B, Kolter J Z. Differentiable MPC for end-to-end planning and control. In: Proceedings of Advances in Neural Information Processing Systems (NIPS). Red Hook, USA: Curran Associates, 2018, 8299–8310
[32]	Incremona G P, Ferrara A, Magni L. MPC for robot manipulators with integral sliding modes generation. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 1299−1307 doi: 10.1109/TMECH.2017.2674701
[33]	Wang B, Deng Y, Chen Z, Liang B. Equilibrium compensation based control: A universal control scheme for systems with mismatched disturbances and sensor errors. IEEE Transactions on Industrial Electronics, 2023, 71(8): 9590−9600
[34]	Demetriou P, Asprou M, Quiros-Tortos J, Kyriakides E. Dynamic ieee test systems for transient analysis. IEEE Systems Journal, 2015, 11(4): 2108−2117
[35]	Pourbeik P, Sanchez-Gasca J J, Senthil J, Weber J, Zadkhast P, Ramasubramanian D. A generic model for inertia-based fast frequency response of wind turbines and other positive-sequence dynamic models for renewable energy systems. IEEE Transactions on Energy Conversion, 2023, 39(1): 425−434
[36]	Dong D, Wen B, Boroyevich D, Mattavelli P, Xue Y. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions. IEEE Transactions on Industrial Electronics, 2014, 62(1): 310−321